Int'l J. of Communications, Network and System Sciences
Vol.2 No.2(2009), Article ID:422,6 pages DOI:10.4236/ijcns.2009.22011
Cooperative Self Encoded Spread Spectrumin Fading Channels
University of Nebraska-Lincoln, Omaha, NE, USA
Email: {khua, wjang, nguyenl}@unlnotes.unl.edu
Received November 15, 2008; revised February 26, 2009; accepted March 3, 2009
Keywords: Cooperative Diversity, Spread Spectrum, Maximum Ratio Combiner
Abstract
Self-encoded spread spectrum (SESS) is a unique realization of random spread spectrum. SESS eliminates the need for the traditional transmitting and receiving PN code generators. Instead, the time varying, random spreading sequence is obtained from the data source. Cooperative diversity (CD) has been attracting increasing attention as a novel and promising diversity technique. This paper analyzes the cooperative SESS for Amplify and Forward CD links in Rayleigh channels. The results show that our cooperative SESS improves the system performance significantly over MRC-based cooperative systems.
1. Introduction
Cooperative diversity receives increasing attention as a diversity enabler, whereby several partner terminals around a given mobile terminal form a distributed cooperative network and transmit information collaboratively [1]. The advantages of CD are similar to existing diversity technique like MIMO to combat the detrimental effects of multipath fading. Sendonaris [2,3] has proposed a user cooperation model that achieved an increase in capacity. As spread spectrum can effectively deal with multipath fading, direct-sequence spread spectrum transmissions have been considered for implementing a novel spectrally efficient cooperative protocol [4]. SESS is a unique random spread spectrum that eliminates the need for traditional transmit and receive PN code generators [5]. In this paper, we consider SESS cooperative diversity (SESS-CD) communication over fading channels and analyze its performance in fading channels. Expressions for the average bit error rate (BER) are derived and the result is compared with the repetition scheme with maximum ratio combiner (MRC). The mobile radio channel suffers from multipath fading, implying that, within the duration of any given call, mobile users could experience severe variations in signal attenuation. Spread spectrum and diversity are methods for combating the detrimental effects of fading. Iterative detection with SESS-CD receiver is shown to achieve remarkable performance improvement reducing the BER significantly. SESS-CD with iterative detection provides both temporal and spatial diversity while MRC exploits only spatial diversity gain.
In Section 2, we describe the system model. Section 3 analyzes the performance of SESS-CD and MRC. The analytical and simulation results based on SESS-CD schemes are presented in Section 4. The conclusion follows in Section 5.
2. System Model
Consider the cooperative network where information is communicated between a source (S=R1) and a destination (D=R0) over a complex channel with fading parameter f10. Two relay nodes, R2 and R3, are willing to cooperate to provide repeated signals through the complex channels with flat fading channel parameters (f12, f13) from (S) to (R2, R3), and (f20, f30) from (R2, R3) to (D), respectively. Without loss of generality, we assume the relays and destination have the same additive white Gaussian noise (AWGN) power. We also assume that the values of random variables, f10, f12, f13, f20 and f30 have been determined at the receiver ends by training. We consider the
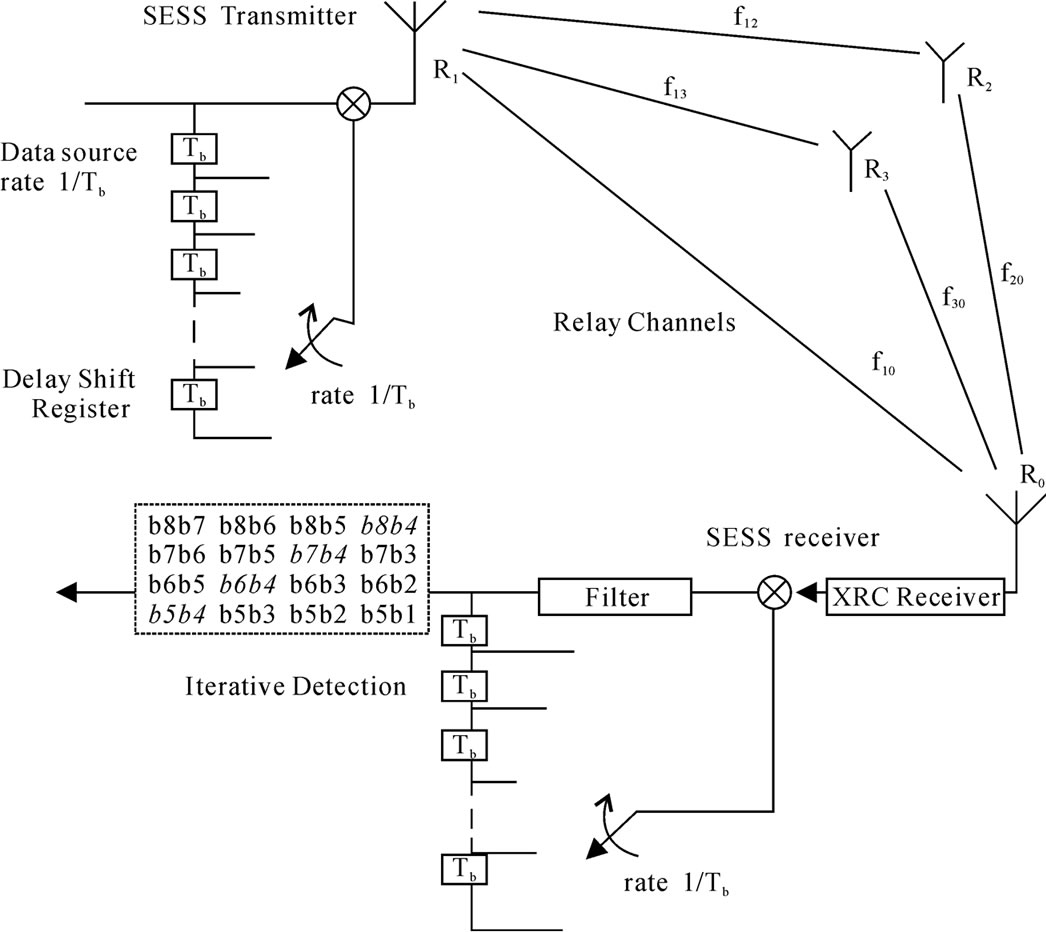
Figure 1. Cooperative self-encoded spread spectrum structure.
Amplify and Forward (AF) model with a constant average power. The basic idea in our proposed spatially cooperative spread spectrum is to implement SESS across a cooperative relay network. Figure 1 shows the block diagram of SESS-CD system. At the transmitter, the delay registers are constantly updated from N-tap serial delay of the data to generate the spreading sequence of length N. The current bit is spread by the time varying N chip sequence that has been obtained from the previous N data bits [6]. The SESS data bit will be transmitted through the direct and relay paths simultaneously with different fading coefficients as shown in Figure 1. The self-encoding operation at the transmitter is reversed at the receiver. The recovered data are fed back to the N-tap delay registers that provide an estimate of the transmitter spreading code required for signal de-spreading. The SESS-CD receiver employs iteration decision. The receiver thus exploits the additional time diversity as well as the spatial diversity inherent in relay systems. The transmitted signal can be expressed as:
x=diSi (1)
where di and Si are the data bit and the SESS spreading sequence, respectively, during i-th bit duration. In MRC scheme, x is a simple data bit. Let the fading amplitude be fij with the corresponding mean of Kij. Then, the received signals can be expressed as:
 (2)
(2)
 (3)
(3)
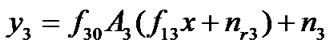 (4)
(4)
where nri is the noise at the relay, and ni is the noise at the destination. nri and ni are statistically independent Gaussian noise which is distributed as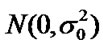 , where we assume the same noise power
, where we assume the same noise power 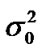 at relays and the destination. A2 and A3 are amplification factors to maintain constant average power output of the relays:
at relays and the destination. A2 and A3 are amplification factors to maintain constant average power output of the relays:
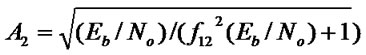
 (5)
(5)
Then, the output of the decorrelator at the receiver is given by
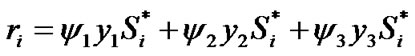 (6)
(6)
where 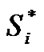 is the recovered spreading sequences at the receiver, which may be different from Si due to detection errors.
is the recovered spreading sequences at the receiver, which may be different from Si due to detection errors.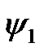 ,
, 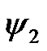 and
and 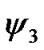 are the normalization factors for fading and noise power:
are the normalization factors for fading and noise power:


 (7)
(7)
We can write SESS signals as
 (8)
(8)
where di are the data bits delayed to form the SESS spreading sequences. Since the current bit is spread by N previous bits, we can observe that current detecting bit d1 is also related to previous N information bits, which are stored in the delay shift register d−N+1,…, d0. By incorporating previous detected bits, we expect to improve the performance. Therefore signal energy can be retrieved from previous estimated bits(ci) as
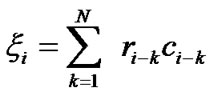 (9)
(9)
and the bit decision can be made based on
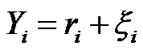 (10)
(10)
For MRC scheme, we obtain
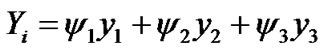 (11)
(11)
at the receiver for bit detection. We assume that each relay path and direct path are isolated. The isolation can be achieved by time division multiplexing.
3. Performance
1) BER for Relay Channel (MRC): As shown in Figure 1, f10, f12, f13, f20 and f30 are the fadings on the relay and direct paths. Let the mean and the second moment (power) of the fading, fij are equal to Kij and ζij, respectively. Then, the signal-to-noise ratio (SNR) at different nodes can be calculated as:
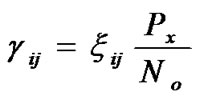 (12)
(12)
where Px /No is the received SNR in AWGN channels without fading. The SNR at receiver with diversity can be derived from [1] as
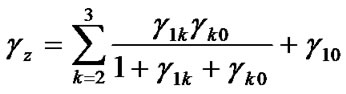 (13)
(13)
which is reduced to
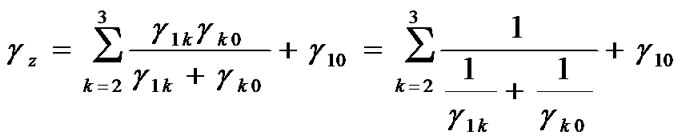 (14)
(14)
at high SNR. In MRC cooperative scheme, information bits are repeated in relay paths. We assume binary phase-shift keying modulation (BPSK) over Rayleigh fading channels. Therefore, the bit error rate with M relay branches is [1]:
 (15)
(15)
where K denotes the factor in non-central Chi-squared distribution, and K=0 for exponential distribution. The constant k depends on the type of modulation, and k =2 for phase shift keying. C(M) can be obtained as
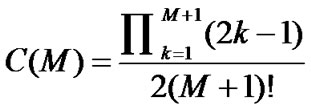 (16)
(16)
If the relay nodes number M=2, then
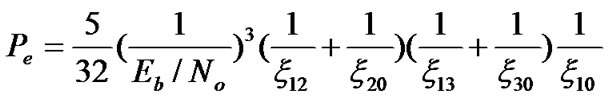 (17)
(17)
We observe that the error probability Pe is the function of (Eb/No)-(M+1) where M is the number of relay nodes. Therefore, the cooperative network can achieve the full diversity order of M +1.
2) BER for Self-encoded Spread Spectrum Cooperative Diversity (SESS-CD): The performance of SESSCD with iterative detection can be considered as
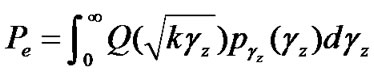 (18)
(18)
where 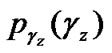 is the probability density function of
is the probability density function of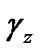 . In this cooperative SESS-CD performance analysis, we do not consider the self-interference that comes from the erroneous despreading sequences due to the incorrect bit decision at the receiver. The self-interference was shown to be dominant at low SNR or with small spreading factors [7]. The received energy in each path can be considered as
. In this cooperative SESS-CD performance analysis, we do not consider the self-interference that comes from the erroneous despreading sequences due to the incorrect bit decision at the receiver. The self-interference was shown to be dominant at low SNR or with small spreading factors [7]. The received energy in each path can be considered as
 (19)
(19)
where 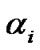 for i=1, ...,N is an exponential random variable (r.v) with parameter
for i=1, ...,N is an exponential random variable (r.v) with parameter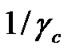 , i.e.,
, i.e.,
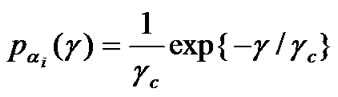 (20)
(20)
where 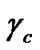 is the chip energy to noise ratio with fading. The
is the chip energy to noise ratio with fading. The 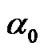 is an exponential r.v. with parameter
is an exponential r.v. with parameter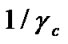 . The first term in Equation (19) is the output of the current bit despreading and the second term is the iterative detection output. We apply the central limit theorem to find the approximate probability density function (pdf) of y. Since the mean and variance of
. The first term in Equation (19) is the output of the current bit despreading and the second term is the iterative detection output. We apply the central limit theorem to find the approximate probability density function (pdf) of y. Since the mean and variance of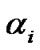 , for i = 1,…N, is
, for i = 1,…N, is 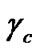 and
and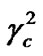 , respectively, we can approximate the mean and variance of y in Equation (19) as
, respectively, we can approximate the mean and variance of y in Equation (19) as
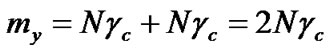 (21)
(21)
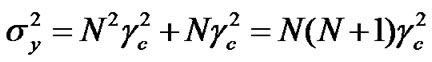 (22)
(22)
Therefore, the approximate pdf of the r.v. y can be obtained as
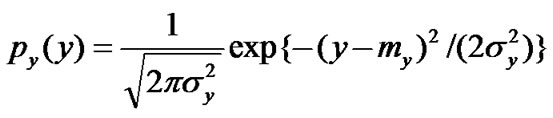 (23)
(23)
Since the first term in Equation (19) is a dominant term, Equation (23) may not be the best approximation. However, we will find that the result can provide a useful insight regarding the SESS-CD diversity gain. For high SNR, py(0) tends to be zero. Therefore, we will find the 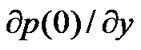 to be applied to the initial value theorem of Laplace Transforms [1] as
to be applied to the initial value theorem of Laplace Transforms [1] as
 (24)
(24)
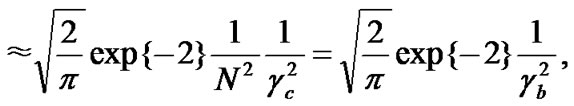 for large N
for large N
where  is the bit energy to noise ratio with fading. The SNR at the different nodes can be represented as
is the bit energy to noise ratio with fading. The SNR at the different nodes can be represented as . With M cooperating branches, the probability of bit error with BPSK can be obtained as
. With M cooperating branches, the probability of bit error with BPSK can be obtained as
 (26)
(26)
where  from Equation (25). C(M) can be obtained as
from Equation (25). C(M) can be obtained as
 (27)
(27)
Comparing Equations (15) and (26), we find that the effective SNR in SESS-CD with iterative detection is the square of the actual SNR.
4. Simulations and Numerical Results
In Figure 2, we can see that the performance of SESSCD is superior to MRC. The result can be predicted from Equations (15) and (26). The BER difference between SESS-CD simulation and analysis comes from the gaussian approximation of the received signal power. The exact pdf and its gaussian approximation of the received signal power over random fading channels are shown in Figure 3. We can observe that the gaussian approximation shifts the probability of low received signal power to high received signal power at both Eb/No equal to 5 dB and 10 dB, while maintaining the same mean and variance as the exact pdf. However the slope of SESS-CD simulation BER and analytical BER agrees well. The diversity gain determines the slope of the BER versus average SNR curve, at high SNR, in a log-log scale. On the other hand, coding gain (in decibels) determines the shift of curve in SNR relative to the benchmark BER curve in uncoded communication over a random fading channel [8]. We see that the Gaussian approximation exhibits a rather accurate diversity gain but not coding gain. The diversity gain in Figure 2 portrays well the square term of the SNR enhancement in SESS-CD in Equation (26). Figure 4 shows the performance of
Figure 2. Simulation BER, SESS-CD (64 chips/bit) and MRC, K10=K20=30=1, K12=K13=1.
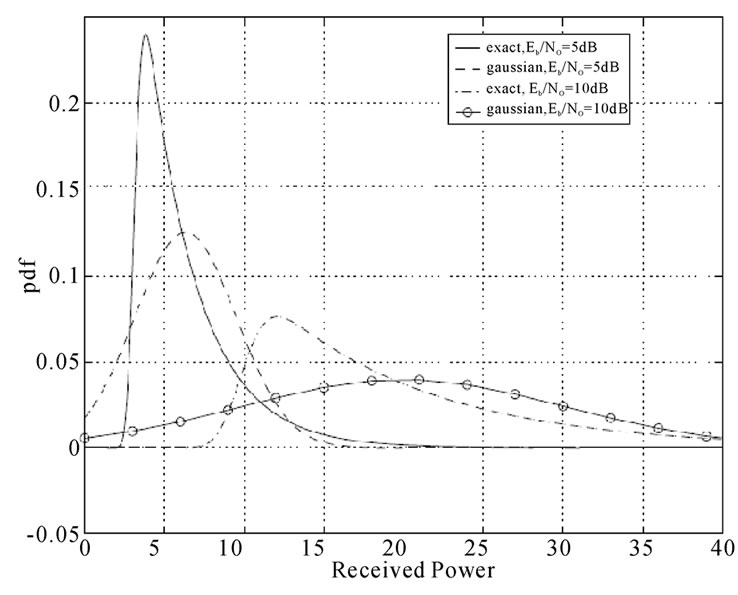
Figure 3. Probability density function of exact pdf and gaussian approximation, 64 chips/bit, Eb/No=5 and 10 dB.

Figure 4. Simulation BER of SESS-CD, 64 chips/bit.

Figure 5. Simulation BER of MRC and SESS-CD (64 chips/bit) with K10 = K20 = K30 = 0.5, K12 = K13 = 0.5, for various correlation values of correlated channel.
SESS-CD with different relay locations. The relay location in the middle of the source and destination (K12 = 0.5, K20=0.5) exhibits a better BER than the relay location near to the source (K12=0.9,K20=0.2). We can also see in Figure 5 that SESS-CD is stable in correlated channels but MRC degrades rapidly as the channel correlation increases. A similar effect can be observed in hostile channels with bit losses in Figure 6 where SESS-CD displays much stable BER performance compared to the MRC.
5. Conclusions
We incorporated SESS with CD in this paper. SESS-CD diversity gain is linked to the square of the received SNR. The SESS-CD BER is inversely proportional to the

Figure 6. Simulation BER of MRC and SESS-CD (64 chips/ bit) with K10=K20=K30=0.5, K12=K13=0.5, under different bit loss percentage.
square term of the SNR while the MRC BER is inversely proportional to the SNR only. We observe that SESS-CD is very stable in highly correlated channels as well as in severely fading channels. SESS combined with CD is obviously a promising CD technique for the future generation of wireless communications.
6. Acknowledgment
This work was supported in part by contract award FA9550-08-1-0393 from the U.S. Air Force Office of Scientific Research. Thanks are due to Dr. J. Sjogren whose support has allowed the authors to investigate the field of cooperative self encoded spread spectrum.
7. References
[1] A. Ribeiro, C. X. Cai, and G. B. Giannakis, “Symbol error probabilities for general cooperative links,” IEEE Transactions on Wireless Communications, Vol. 4, No. 3, pp. 1264-1273, May 2005.
[2] A. Sendonaris, E. Erkip, and B. Aazhang, “User cooperation diversity-Part I: System description,” IEEE Transactions on Communications, Vol. 51, No. 11, pp. 1927-1938, November 2003.
[3] A. Sendonaris, E. Erkip, and B. Aazhang, “User cooperation diversity part II: Implementation aspects and performance analysis,” IEEE Transactions on Communications, Vol. 51, No. 11, pp. 1939-1948, November 2003.
[4] A. Ribeiro , X. Cai, and G. B. Giannakis, “Opportunistic multipath for bandwidth-efficient cooperative networking,” IEEE International Conference on Acoustics Speech and Signal Processing, Montreal, Canada, May 2004.
[5] L. Nguyen, “Self-encoded spread spectrum and multiple access communication,” IEEE 6th International. Symposium on Spread-Spectrum Techniques & Applications, New Jersey, September 2000.
[6] K. Hua, L. Nguyen, W. M. Jang, “Self-encoded spread spectrum synchronization with genetic algorithm and markov chain analysis,” IEEE 42th Conference on Information Science and Systems, Princeton, New Jersey, March 2008.
[7] Y. Kong, L. Nguyen, and W. M. Jang, “On the BER of self-encoded spread spectrum communication systems,” Proceedings of the IASTED International Conference, Wireless and Optical Communications, Banff, Alberta, Canada, June 27-29, 2001.
[8] Z. Wang and G. B. Giannakis, “A simple and general parameterization quantifying performance in fading channels,” IEEE Transactions on Communications, Vol. 51, No. 8, pp.1389-1398, August 2003.

