Int'l J. of Communications, Network and System Sciences
Vol.2 No.1(2009), Article ID:177,7 pages DOI:10.4236/ijcns.2009.21001
Game Theoretic Analysis of Joint Rate and PowerAllocation in Cognitive Radio Networks
School of Information and Science Technology
Sun Yat-Sen University, Guangzhou, China
E-mail: lid3@mail2.sysu.edu.cn
Received September 10, 2008; revised November 26, 2008; accepted December 30, 2008
Keywords: Rate Allocation, Power Allocation, Cognitive Radio, Game Theory
Abstract
Spectrum sharing is an essential enabling functionality to allow the coexistence between primary user (PU) and cognitive users (CUs) in the same frequency band. In this paper, we consider joint rate and power allocation in cognitive radio networks by using game theory. The optimum rates and powers are obtained by iteratively maximizing each CU’s utility function, which is designed to guarantee the protection of primary user (PU) as well as the quality of service (QoS) of CUs. In addition, transmission rates of some CUs should be adjusted if corresponding actual signal-to-interference-plus-noise ratio (SINR) falls below the target SINR. Based on the modified transmission rate for each CU, distributed power allocation is introduced to further reduce the total power consumption. Simulation results are provided to demonstrate that the proposed algorithm achieves a significant gain in power saving.
1. Introduction
Conventional fixed spectrum allocation policy has recently resulted in the intense competition for the use of radio spectrum due to the increasing number of various bandwidth-consuming wireless services. Moreover, these bands are not occupied or underutilized by licensed users most of time. According to the study from Federal Communication Commission (FCC) [1], the utilization of licensed bands ranges from 15% to 85%. In order to alleviate the problem of spectrum scarcity and improve the spectrum utilization, cognitive radio has been proposed as a flexible spectrum usage model [2-4]. In this technique, cognitive (unlicensed) user (CU) are allowed to have opportunistic access to idle spectrums or to the busy ones without causing harmful interference to the primary (licensed) user (PU). The major advantage of cognitive radio technology is its ability to search available spectrums in its surrounding environment and adjust its transmit parameters accordingly to enhance the system performance. The transmit parameters, for example, include modulation scheme, beamforming weight center frequency, transmit power and so on. In this paper, we focus on the allocation of transmission rate and power in cognitive radio networks. In particular, in such spectrum sharing model where CU operating in the same frequency band with PU, these transmit parameters should be adjusted to maintain interference introduced to PU within a given limit while satisfying the quality of service (QoS) of CU. Therefore, interference introduced by multi-user or co-channel transmission at the same time or over the same frequency radio channel is inevitable.
In this paper, we consider applying game theory to spectrum sharing in cognitive radio networks by adjusting transmission rate and power. Related works are shown in [5-6]. In [5] and [6], two different distributed power allocation algorithms are investigated in a game theoretic perspective, with regard to the idle and busy spectrum, respectively. However, these power allocation algorithms are not effective in guaranteeing the QoS of CUs in bad channel conditions, due to the rigid target signal-to-interference-plus-noise ratio (SINR) constraint. Further studies are given in [7-9], in which joint rate and power allocation has been considered by using game theory. These works can be applied to the systems where only CUs share the same frequency band with the absence of PU. Unfortunately, they can not be extended to the scenario of the co-existence of PU and multiple CUs in the same frequency band, since they do not
Figure 1. System model with one PU in dashed line and N CUs in solid line.
consider the protection of PU. While literature [10] and [11] only consider the problem of joint rate and power allocation of a single CU in the presence of PU, where there is no competition for the available spectrum resource among multiple CUs.
In this contribution, our goal is, therefore, to jointly optimize the transmission rates and power levels in order to accommodate CUs as many as possible, while guaranteeing the protection of PU and the QoS of CUs. In this paper, we first formulate the problem as a supermodular game [5] which is proved to have at least a Nash Equilibrium (NE), and then give the solution by maximizing the utility function for each CU. After the adjustment of transmission rate, the improved SINR is assured to converge to the predefined target SINR for each CU. It will demonstrate that the distributed power allocation algorithm [12] based on the adaptive transmission rate can further reduce the total power consumption. The major advantage of our proposed algorithm is that it is implemented in a totally distributed manner without the need of access point (AP) [13], and its computational complexity is low since the transmit powers require only few iterations to converge.
The rest of this paper is organized as follows: Section 2 presents the system model and basic assumptions. Section 3 formulates the problem using game theory. In Section 4. we develop the proposed algorithm for joint rate and power allocation in cognitive radio networks. Performance analysis of the proposed algorithm is investigated in Section 5. Section 6 concludes this paper.
Notation: All vectors and matrices are denoted in bold letters.  stands for
stands for  identity matrix.
identity matrix.  denotes the
denotes the  thelement of the matrix
thelement of the matrix .
.
2. System Model
The cognitive radio network under consideration is composed of one PU and N CUs, which are modeled as a collection of separate (N+1) transmit-receive pairs with a single channel, as illustrated in Figure 1. All CUs are allowed to transmit at the same time and share the same frequency band by adopting code division multiplexing access (CDMA). The transmission mode for each CU is half-duplex in order to avoid self-interference [14] caused by one node simultaneously transmitting and receiving. The channel propagation model is characterized by average path loss, which is given by [15]
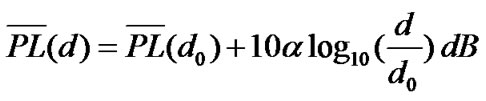
 (1)
(1)
where 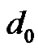 and
and 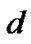 are the reference and transmitterreceiver (T-R) distance, respectively.
are the reference and transmitterreceiver (T-R) distance, respectively. 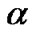 denotes path loss exponent, which depends on propagation circumstance.
denotes path loss exponent, which depends on propagation circumstance.
Then, the actual SINR for ith CU can be expressed as
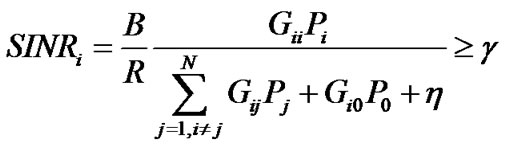 (2)
(2)
where  and
and 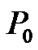 denote power level of ith CU and PU, respectively.
denote power level of ith CU and PU, respectively. 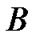 is the spectrum bandwidth,
is the spectrum bandwidth, 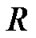 is the transmission rate and
is the transmission rate and 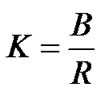 denotes the spreading gain.
denotes the spreading gain. is the channel gain over CU i,
is the channel gain over CU i,  and
and 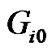 represent the channel gain between CU j’ transmitter, PU’s transmitter and CU i’ receiver, respectively.
represent the channel gain between CU j’ transmitter, PU’s transmitter and CU i’ receiver, respectively.  is the background noise power.
is the background noise power. 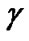 is the target SINR for all CUs and the constraint
is the target SINR for all CUs and the constraint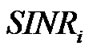 ≥
≥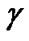 guarantee the QoS for ith CU. On the other hand, the total interference introduced to PU is given by
guarantee the QoS for ith CU. On the other hand, the total interference introduced to PU is given by
 (3)
(3)
where 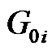 represents the channel gain between CU i’ transmitter and PU’s receiver and
represents the channel gain between CU i’ transmitter and PU’s receiver and 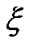 denotes the maximum tolerable interference introduced to PU.
denotes the maximum tolerable interference introduced to PU.
Throughout this paper, we make the following assumptions:
• The local information of channel gains and SINR measurements at the receivers of all CUs are sent to their respective transmitters via a dedicated feedback channel.
• All CUs are well synchronized, are assumed to be immobile or move slowly so that the corresponding channel gain remains constant during the convergence of transmit powers.
3. Game Formulation
The objective of this algorithm is to assign constrained transmit powers and available transmission rates to all CUs, in order to minimize the total power consumptions while satisfying the target SINR constraint of CUs. Besides, we should also consider maintaining the interference introduced to the PU within a given interference limit, since CUs coexist with the PU in the same frequency band. Therefore, we can formulate the following constrained optimization problem.
minimize
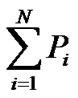 (4)
(4)
subject to
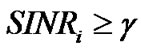 (5)
(5)
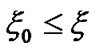 (6)
(6)
where 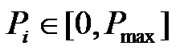 and
and  is the maximum transmit power.
is the maximum transmit power.
In what follows, we start with introducing three basic elements in this game, and then prove the existence of Nash Equilibrium (NE). Finally we will give the solution to this game based on the above analysis.
3.1. Elements of the Game
In normal form, a game consists of three elements in the following way.

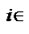
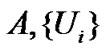
 (7)
(7)
where 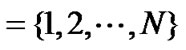
 is the set of players,
is the set of players, 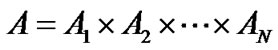 denotes action space for all players with
denotes action space for all players with  presenting the set of action of player i, while
presenting the set of action of player i, while 

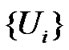 is the set of utility functions.
is the set of utility functions.
More specifically in this game, the set of players 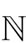 is given by the set of CUs. The action for each player (or CU) is denoted as
is given by the set of CUs. The action for each player (or CU) is denoted as . In order to capture each CU’s satisfaction with both the constraints (5) and (6), the utility function of player
. In order to capture each CU’s satisfaction with both the constraints (5) and (6), the utility function of player 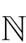
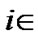 is expressed as
is expressed as
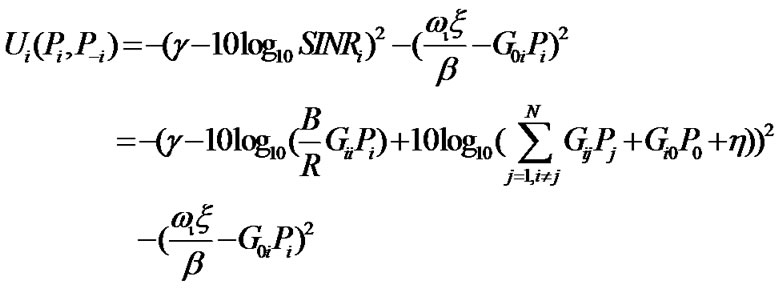 (8)
(8)
where 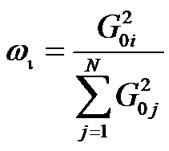 is the weighted coefficient and
is the weighted coefficient and 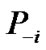 represents the actions for all players except i. Note that the utility function in [7] only considers the QoS of CUs without guaranteeing the protection of PU. In Equation (8),
represents the actions for all players except i. Note that the utility function in [7] only considers the QoS of CUs without guaranteeing the protection of PU. In Equation (8),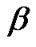 ≥1 is a constant, and the interference constraint of PU can be easily satisfied by increasing the value of
≥1 is a constant, and the interference constraint of PU can be easily satisfied by increasing the value of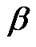 , because the powers allocated to all CUs are kept at a low level. However, it does not mean that large
, because the powers allocated to all CUs are kept at a low level. However, it does not mean that large  might not satisfy the target SINR requirement for all CUs.
might not satisfy the target SINR requirement for all CUs.
3.2. Existence of Nash Equilibrium
Nash Equilibrium is the steady state in the game, in which no player can increase its utility function from unilaterally deviating its action. Mathematically speaking, NE is an action-tuple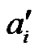 , which satisfies the following property
, which satisfies the following property
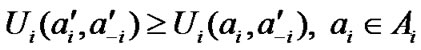 (9)
(9)
However, it does not follow that there is a NE existing in every game. Therefore, it becomes necessary to testify the existence of NE.
Theorem 1: 


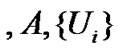
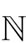
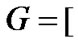 is a supermodular game.
is a supermodular game.
Proof: The action space is compact since it is both closed and bounded. In addition, the utility function of player 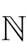
 is twice differentiable.
is twice differentiable.
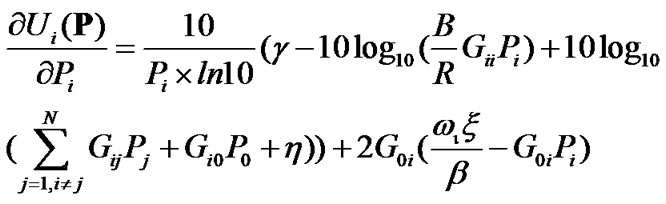 (10)
(10)
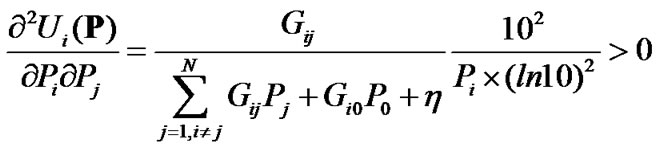 (11)
(11)
According to the definition and property of game modes in [7], this game is a supermodular game and there must be at least one NE in this supermodular game.
3.3. Solution to the Game
Since the existence of NE in this game has been proved, we consider the problem of how to identify it. The optimum transmit power or NE can be obtained in such a way that each CU maximizes its corresponding utility function iteratively, which is assured to converge assuming each CU acts in its own interest. Mathematically speaking, the process can be expressed in the following way.
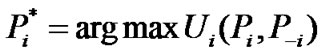 ,
,
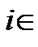 (12)
(12)
where .
.
It should be noted that there is no sufficient guarantee in this game with regard to constraint (5) and (6). First, the protection of PU is not assured if 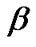 is not set appropriately. Second, due to the rigid SINR requirement of each CU, the corresponding QoS of some CUs which experience strong interference or deep path loss will be violated. In the next section, we will give details to solve these problems.
is not set appropriately. Second, due to the rigid SINR requirement of each CU, the corresponding QoS of some CUs which experience strong interference or deep path loss will be violated. In the next section, we will give details to solve these problems.
4. Joint Rate and Power Allocation Algorithm
In this section, we perform a two-stage processing to make sure that both the interference constraint of PU and SINR constraint of CUs are satisfied. The transmit power is first allocated to each CU using Equation (12), in which the transmission rate is the same for each CU. If the PU experience harmful interference, the value of 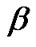 and transmit power in Equation (8) are both updated until the interference introduced to PU is kept at an acceptable level. If the QoS of some CUs are not guaranteed, the transmission rate is adjusted so that the corresponding actual SINR is no less than the target SINR. Besides, it will be demonstrated that the total power consumption is greatly reduced by iteratively update powers based on the modified transmission rate and convergent power first allocated for each CU, while the constraint (5) and (6) can also be satisfied. The whole process can be summarized as follows.
and transmit power in Equation (8) are both updated until the interference introduced to PU is kept at an acceptable level. If the QoS of some CUs are not guaranteed, the transmission rate is adjusted so that the corresponding actual SINR is no less than the target SINR. Besides, it will be demonstrated that the total power consumption is greatly reduced by iteratively update powers based on the modified transmission rate and convergent power first allocated for each CU, while the constraint (5) and (6) can also be satisfied. The whole process can be summarized as follows.
1. Initialize: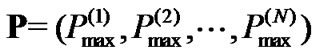 ,
,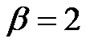 ;
;
2. Calculate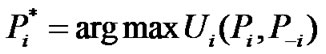 ,
,
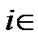 ;
;
3. If both the constraints (5) and (6) are satisfied, stop;
4. elseif constraint (5) is not satisfied
5. evoke rate allocation process;
6. elseif constraint (6) is not satisfied
7. 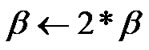 , go to 2;
, go to 2;
8. end if 9. evoke power allocation process
4.1. Rate Allocation
Rate allocation enables the system to support various data rates by varying the number of bits per second in accordance with the instantaneous SINR. In this case, the actual SINR for ith CU can be rewritten in the following way.
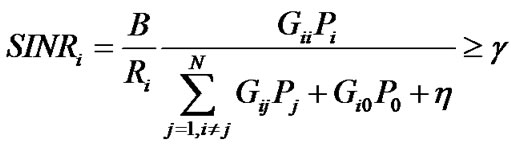 (13)
(13)
where 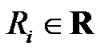 and
and 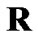 denotes the set of available transmission rates. Here,
denotes the set of available transmission rates. Here, 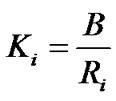 represents the spreading gain for ith CU. In this paper, we assume each CU is equipped with the Walsh-Hadamard code and a set of different processing gains denoted as
represents the spreading gain for ith CU. In this paper, we assume each CU is equipped with the Walsh-Hadamard code and a set of different processing gains denoted as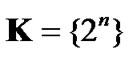 , where
, where 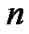 is the positive integer. Therefore, the available transmission rates in
is the positive integer. Therefore, the available transmission rates in  can be obtained in such a way that
can be obtained in such a way that 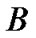 is divided by the corresponding processing gain in
is divided by the corresponding processing gain in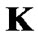 .
.
As mentioned before, due to the rigid target SINR constraint, some CUs in bad channel conditions can not satisfy the QoS requirement, in which the transmission rate is the same for each CU and chosen to be the maximum one in 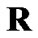 (or equivalently the minimum processing gain in
(or equivalently the minimum processing gain in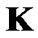 ). In order to achieve all CUs’ convergence to the target SINR, the transmission rate should be adjusted according to the convergent power for each CU. Specifically, the adjusted transmission rate is determined in such a way that the corresponding improved SINR is no less than
). In order to achieve all CUs’ convergence to the target SINR, the transmission rate should be adjusted according to the convergent power for each CU. Specifically, the adjusted transmission rate is determined in such a way that the corresponding improved SINR is no less than . In this case, there may be many available transmission rates which satisfy the above requirement, and the maximum one should be chosen from them in order to achieve the transmission rate as high as possible. If the improved SINR still falls below
. In this case, there may be many available transmission rates which satisfy the above requirement, and the maximum one should be chosen from them in order to achieve the transmission rate as high as possible. If the improved SINR still falls below , the corresponding CU will be switched off, for its QoS requirement can not be met. Therefore, the target SINR constraint of all CUs can be satisfied.
, the corresponding CU will be switched off, for its QoS requirement can not be met. Therefore, the target SINR constraint of all CUs can be satisfied.
4.2. Power allocation
Since the constraint (5) and (6) are both satisfied as discussed before, we consider further reducing the total power consumption for all CUs. Then, the constraint (5) can be expressed in the following way
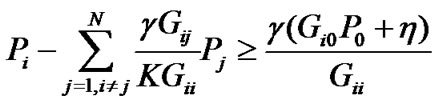 (14)
(14)
Note that the target SINR is not the same for all CUs in this stage. Let , rewrite (14) with equality in the matrix form, we can obtain
, rewrite (14) with equality in the matrix form, we can obtain
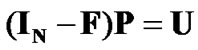 (15)
(15)
where  and
and 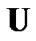 are given by
are given by
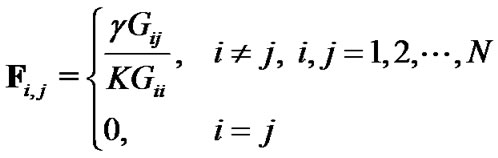 (16)
(16)
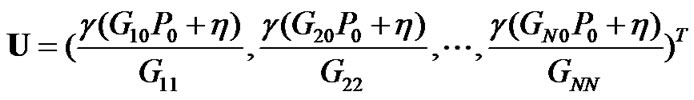 (17)
(17)
The Equation (15) can be rewritten in the following form as
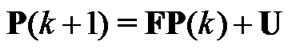 (18)
(18)
where 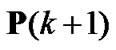 and
and 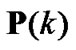 denote the vector of power level at next and current iteration, respectively. Then, the optimal transmit power can be obtained by iteration of [5]
denote the vector of power level at next and current iteration, respectively. Then, the optimal transmit power can be obtained by iteration of [5]
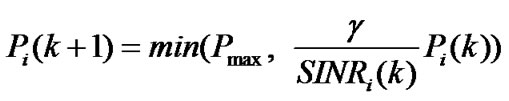 (19)
(19)
Note that the above algorithm terminate with convergent power if , where
, where 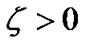 is a negligibly small error. Based on powers first allocated to all CUs and improved SINR which satisfies the constraint (5), it can be known that the total power consumption will be reduced after second allocation of powers using Equation (19) in which the first allocated powers using Equation (12) are used as initialized powers. The following theorem supports our conclusion.
is a negligibly small error. Based on powers first allocated to all CUs and improved SINR which satisfies the constraint (5), it can be known that the total power consumption will be reduced after second allocation of powers using Equation (19) in which the first allocated powers using Equation (12) are used as initialized powers. The following theorem supports our conclusion.
Theorem 2: Given  and corresponding
and corresponding 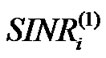 satisfying
satisfying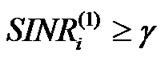 ,
, 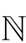
 , then there exists a steady
, then there exists a steady
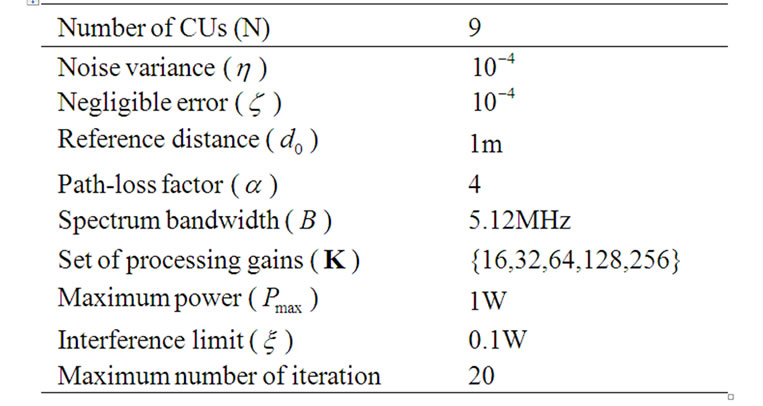
Table 1. Simulation parameters.
state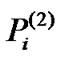 to achieve
to achieve 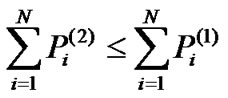 while satisfying both the constraint (5) and (6).
while satisfying both the constraint (5) and (6).
Proof: It can be known from Equation (19) that, if SINR for each CU satisfies the condition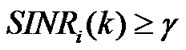 , then we have
, then we have
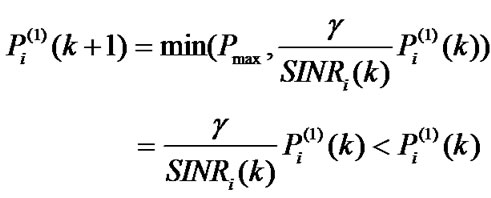
The iteration will terminate if there is no negligible change in 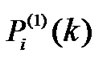 such that
such that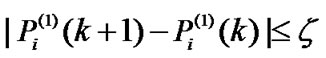 . That is to say that
. That is to say that 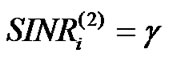 when transmit power converges, so that constraint (5) is satisfied. Therefore, the convergent power
when transmit power converges, so that constraint (5) is satisfied. Therefore, the convergent power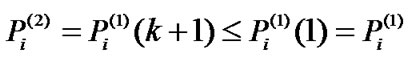 . As a result, we have
. As a result, we have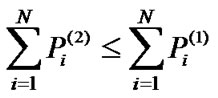 , and the constraint (6) is also satisfied with
, and the constraint (6) is also satisfied with 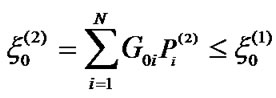
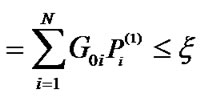 .
.
5. Simulation Results
In this section, we provide numerical results to demonstrate the effectiveness of the proposed algorithm in reduction of the total power consumption while satisfying both the target SINR constraint of CUs and interference constraint of PU. In our simulation, we consider the cognitive radio network placed in a 10m×10m square area, in which transmit nodes are located uniformly and the corresponding receive nodes are random placed within 6m×6m square area centered around them. The specific parameters used in this simulation are listed in Table 1, in which the channel gain can be expressed as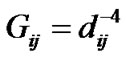 , where
, where 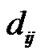 is the distance between jth CU’s transmitter and ith CU’s receiver. According to Table 1, the available transmission rates can be obtained with the result of
is the distance between jth CU’s transmitter and ith CU’s receiver. According to Table 1, the available transmission rates can be obtained with the result of  ={320, 160,80,40,20} kbps.
={320, 160,80,40,20} kbps.
First, we examine the convergence performance of proposed game model with respect to transmit power and actual SINR for each CU, which are illustrated in Figure 2 (a) and (b), respectively. Figure 2 (a) shows that the transmit power for each CU converges to the steady state after several iterations, in which the transmission rate is 320 kbps and the corresponding processing gain is accordingly 16 for each CU. From Figure 2 (a), we observe that there are 5 CUs still transmitting at the maximum power. This is because these CUs experience strong interference or deep path loss, and the corresponding transmit power should be kept at a high level in order to satisfy the SINR constraint. From Figure 2 (b), we can find that the actual SINR of each CU can not converge to the predefined 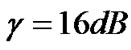 at the same time, no matter how high the corresponding transmit power is. This is due to the hard target SINR constraint as mentioned before. Note that,
at the same time, no matter how high the corresponding transmit power is. This is due to the hard target SINR constraint as mentioned before. Note that, 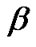 is set to be 2 and there is no need to update
is set to be 2 and there is no need to update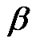 , because, in this case, the total interference introduced to PU is 0.0112 W which satisfies the constraint (6).
, because, in this case, the total interference introduced to PU is 0.0112 W which satisfies the constraint (6).
Next, we investigate the convergence performance of the proposed algorithm with respect to transmit power and improved SINR for each CU, which are illustrated in Figure 3(a) and (b), respectively. Figure 3(a) shows that, by adjusting the corresponding transmission rate, more power can be saved after the convergence of (19). To be specific, the total power consumption is greatly reduced from 5.9 W to 0.5408 W. Here, the total interference is 0.0012 W. Note that in Figure 3(a), the inputs are the convergent transmit powers in Figure 2(a) with improved SINR satisfying constraint (5). As for Figure 3(b), the adjusted transmission rates for all CUs are 320, 160, 80, 40, 160, 0, 0, 0 and 160 kbps, which correspond to the processing gain 16, 32, 64, 128, 32, 0, 0, 0 and 32, respectively. It should be noted that 3 CUs are switched off, in which the corresponding improved SINR still falls below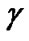 . As can be seen from Figure 3(b), the improved SINRs for the remainder of CUs all converge to
. As can be seen from Figure 3(b), the improved SINRs for the remainder of CUs all converge to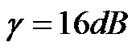 , and we can find that more CUs are permitted to transmit after the adjustment of their corresponding transmission rates compared with Figure 2(b).
, and we can find that more CUs are permitted to transmit after the adjustment of their corresponding transmission rates compared with Figure 2(b).
In our simulations so far, the constant transmit power of PU  and target SINR
and target SINR 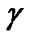 are assumed. To be more practical, we finally study the impact of different
are assumed. To be more practical, we finally study the impact of different 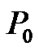 and
and 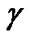 on the performance of proposed game model in terms of the total power consumption. Figure 4 depicts the total transmit power versus different
on the performance of proposed game model in terms of the total power consumption. Figure 4 depicts the total transmit power versus different 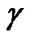 after the convergence of (12), where
after the convergence of (12), where 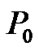 is varied at 10W, 20W and 30W, respectively. As can be seen from Figure 4, the total power consumption increases with the increasing value of
is varied at 10W, 20W and 30W, respectively. As can be seen from Figure 4, the total power consumption increases with the increasing value of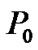 . This is because the interference introduced to each CU increases as
. This is because the interference introduced to each CU increases as 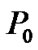 is increased, which means that each CU will increase its transmit power accordingly, in order to satisfy the target SINR constraint. Besides, we also notice that the total power consumption increases with the increasing value of
is increased, which means that each CU will increase its transmit power accordingly, in order to satisfy the target SINR constraint. Besides, we also notice that the total power consumption increases with the increasing value of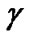 . This is due to the fact that the transmit power should be increased so that the corresponding target SINR requirement can be met.
. This is due to the fact that the transmit power should be increased so that the corresponding target SINR requirement can be met.
6. Conclusions
In this paper, we have proposed and investigated a joint rate and power allocation algorithm in cognitive radio networks by using game theory. The objective of the proposed algorithm is to minimize the total power consumption, while satisfying the target SINR constraint of CUs and keeping the interference introduced to PU below a given limit. We have analyzed the problem as a super-modular game and obtained the NE which leads to the optimal transmit powers. In order to solve the
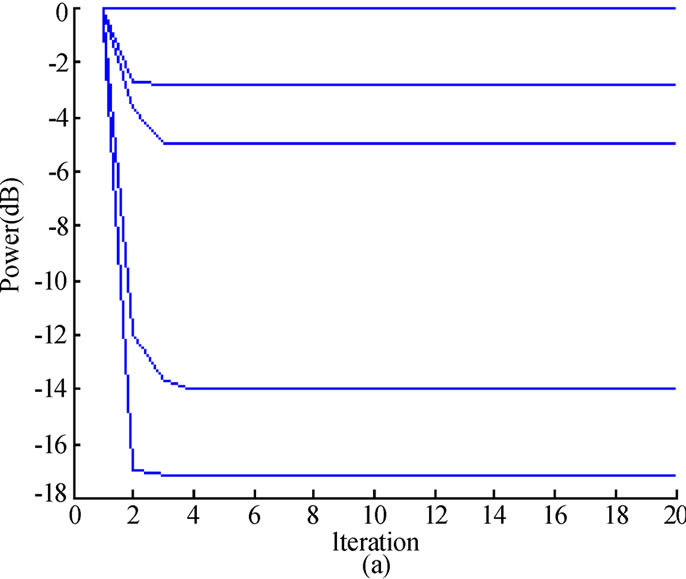
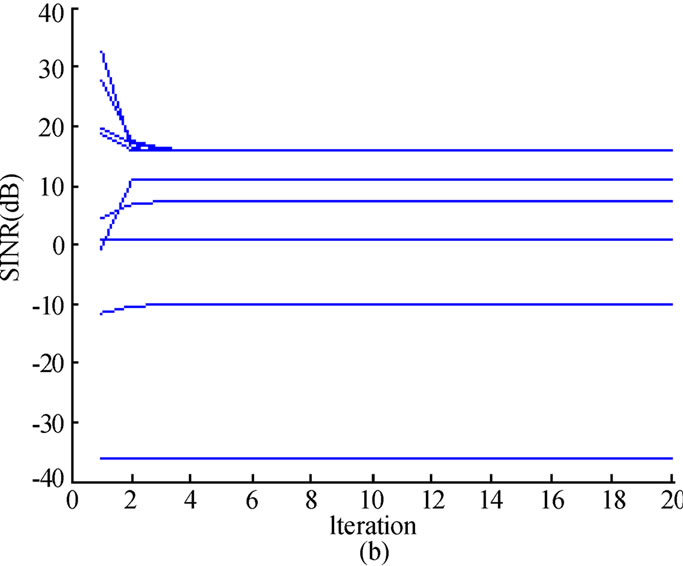
Figure 2. Convergence of transmit power and actual SINR for each CU using Equation (12), where  and
and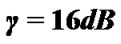 . (a) Transmit Power (dB). (b) Actual SINR (dB).
. (a) Transmit Power (dB). (b) Actual SINR (dB).
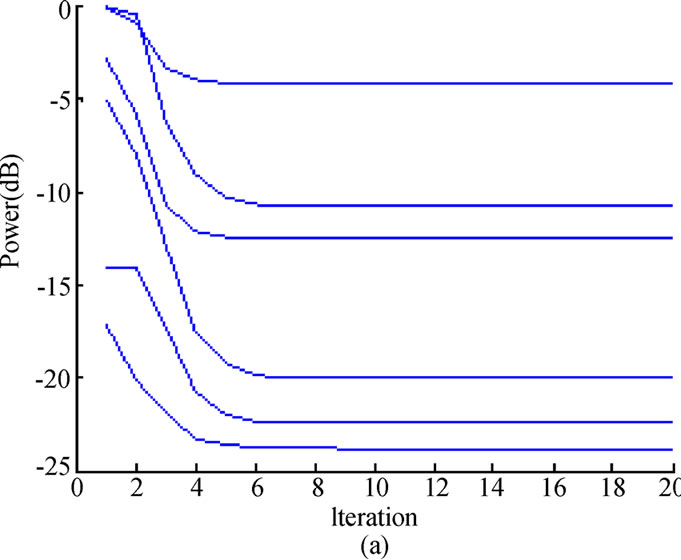

Figure 3. Convergence of transmit power and improved SINR for each CU using Equation (19), where  and
and . (a) Transmit power (dB). (b) Actual SINR (dB).
. (a) Transmit power (dB). (b) Actual SINR (dB).
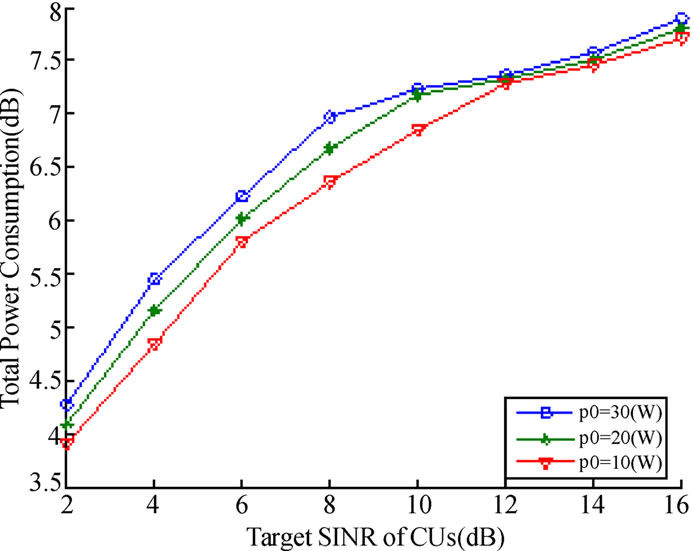
Figure 4. Convergence of total transmit power versus different target SINR 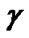 after the convergence of (12).
after the convergence of (12).
inherent  - divergence problem, the distributed power allocation algorithm with adaptive transmission rate has been introduced, which has been proved to achieve significant improvement in the power efficiency. Simulation results are shown to confirm the effectiveness of the proposed algorithm.
- divergence problem, the distributed power allocation algorithm with adaptive transmission rate has been introduced, which has been proved to achieve significant improvement in the power efficiency. Simulation results are shown to confirm the effectiveness of the proposed algorithm.
7. Acknowledgement
This work is supported by the National Science Foundation of China (NSFC), Grant 60772132, and the joint foundation of National Science Foundation of China (NSFC) and Guangdong Province U0635003, and also supported by the Science & Technology Project of Guangdong Province, Grant 2007B010200055.
8. References
[1] Federal Communications Commission, “Spectrum Policy Task Force,” Reports, ET Docket No. 02-135, November 2002.
[2] J. Mitola and G. Q. Maguire, “Cognitive radio: Making software radios more personal,” IEEE Personal Communications, Vol. 6, No. 4, pp. 13–18, August 1999.
[3] J. Mitola, “Cognitive radio: An integrated agent architecture for software defined radio,” Tekn. Dr. dissertation, Royal Institute of Technology (KTH), Stockholm, Sweden, 2000.
[4] S. Haykin, “Cognitive radio: Brain-empowered wireless communications,” IEEE Journal on Selected Areas in Communications, Vol. 23, No. 2, pp. 201-220, February 2005.
[5] J. Neel, R. Menon, J. H. Reed, and A. B. MacKenzie, “Using game theory to analyze physical layer cognitive radio algorithms,” [Online], available:
http://web.syr.edu/~ejhumphr/.
[6] H. Li, Y. Gai, Z. He, K. Niu, and W. Wu, “Optimal power control game algorithm for cognitive radio networks with multiple interference temperature limits,”
in Proceedings of IEEE Vehicular Technology Conference, pp. 1554-1558, May 2008.
[7] M. Hayajneh and C. T. Abdallah, “Distributed joint rate and power control game-theoretic algorithms for wireless data,” IEEE Communications Letters, Vol. 8, No. 8, pp. 511–513, August 2004.
[8] M. R. Musku, A. T. Chronopoulos, and D. C. Popescu, “Joint rate and power control with pricing,” in Proceedings of IEEE Global Telecommunications Conference, pp. 3466-3470, November 2005.
[9] M. R. Musku, A. T. Chronopoulos, and D. C. Popescu, “Joint rate and power control using game theory,” in Proceedings of IEEE Consumer Communications and Networking Conference, pp. 1258-1262, January 2006.
[10] L. Guo, P. Wu, and S. Cui, “Power and rate control with dynamic programming for cognitive radios,” in Proceedings of IEEE Global Telecommunications Conference, pp. 1699-1703, November 2007.
[11] M. Hong, J. Kim, H. Kim, and Y. Shin, “An adaptive transmission scheme for cognitive radio systems based on interference temperature model,” in Proceedings of IEEE Consumer Communications and Networking Conference, pp. 69-73, January 2008.
[12] G. J. Foschini and Z. Miljanic, “A simple distributed autonomous power control algorithm and its convergence,” IEEE Transactions on Vehicular Technology, Vol. 42, No. 4, pp. 641-646, November 1993.
[13] IEEE 802.22 Working Group on Wireless Regional Area Networks, http://www.ieee802.org/22.
[14] T. ElBatt and A. Ephremides, “Joint scheduling and power control for wireless ad hoc networks,” IEEE Transactions on Wireless Communications, Vol. 3, No. 1, pp. 74-85, January 2004.
[15] T. S. Rappaport, Wireless communications principles and practice, Prentice Hall Inc., 1996.

