Creative Education
2012. Vol.3, No.3, 380-382
Published Online June 2012 in SciRes (http://www.SciRP.org/journal/ce) http://dx.doi.org/10.4236/ce.2012.33060
380
Playing Around with “Kaleidagraph” Program for Determination
of pKa Values of Mono, Di and Tri Basic Acids in a
Physical-Organic Chemistry Laboratory
Vandanapu Jagannadham1*, Rachuru Sanjeev2
1Department of Chemistry, Osmania University, Hyderabad, India
2Department of Chemistry, Mizan-Tepi University, Tepi Campus, Tepi, Ethiopia
Received March 5th, 2012; revised April 8th, 2012; accepted April 28th, 2012
A simple and easy laboratory protocol for the determination of the pKa of mono, di and tri-basic weak ac-
ids is described in this paper by using arbitrarily simulated data as a function of pH. An equation com-
patible to Kaleidagraph program is derived and used in the program to determine the pKa. The present
protocol for the determination of the pKa is useful in teaching chemistry experiments in a Physical-Or-
ganic Chemistry Laboratory.
Keywords: pKa; Kaleidagraph; Acid-Base Equilibriums
Introduction
The acid-base ionization/dissociation constant, pKa, is a
measure of the tendency of a molecule or ion to keep a proton
(H+) at its ionization center(s), and is related to the ionization
ability of the acid or base. pKa is the core property of an elec-
trolyte that defines chemical and biological behavior. In bio-
logical terms, pKa is important in determining whether a mole-
cule will be taken up by aqueous tissue components or lipid
membranes and is related to log p (where p the partition coeffi-
cient). Water is a very polar solvent (dielectric constant 20 =
80), so facile ionization will increase the likelihood of a species
to be taken up into aqueous solution. If a molecule does not
readily ionize, it will tend to stay in a non-polar solvent such as
cyclohexane (20 = 2) or octanol (20 = 10). Separation and
analytical scientists require an understanding of pKa because it
impacts the choice of techniques used to identify and isolate the
compound of interest. pKa is also closely related to the concept
of pH (the acidity of the solution). Hence the knowledge of pKa
values is useful to the majority of the pharmaceutical compa-
nies worldwide. Also knowing the acidity constant value (Ka)
of an acid and its associated pKa value is important for medical
students for different reasons. The first reason is that the
knowledge of pKa of a drug allows predicting the absorption,
bio-reactivity and tissular accumulation as a function of the pH
of the medium (Brunton, Lazo, & Parker, 2006). Another rea-
son is that the pKa values of the amino acids of a polypeptide
chain are related to the function and structure of the protein
(Stryer, 2003). In addition, the pKa values of different chemical
species will help understanding the biological systems (Devlin,
2003; Guyton, 2006).
Experimental
The software program used for the curve fitting of the simu-
lated data versus pH was a “Kaleidagraph” from Synergy Soft-
ware, Reading, PA, USA.
Results and Discussion
Theoretical Basis: The students must be familiar with the
acid-base equilibriums. Population of dissociated and un-dis-
sociated species of weak acids changes with pH.
Consider the dissociation of a mono-basic weak acid in
aqueous solution,
23
HAH OH OA
K
 


 (1)
The equilibrium constant K could be written as

3
2
HO[A]
HA [H O]
K



 (2)
or
 
3
2
HO A
HO HA K





(3)
or

3
HO A
HA
a
K


 

 
 (4)
where Ka is the acid dissociation constant, [H3O+] is the con-
centration hydrogen ion, [A−] is concentration of salt, and [HA]
is that of un-dissociated acid. Taking the logarithms of Equation
(4), we get




3
HOlogsaltlolog lacogg
a
K



id (5)
or



ppHlog
acid
salt
a
K (6)
*Corresponding author.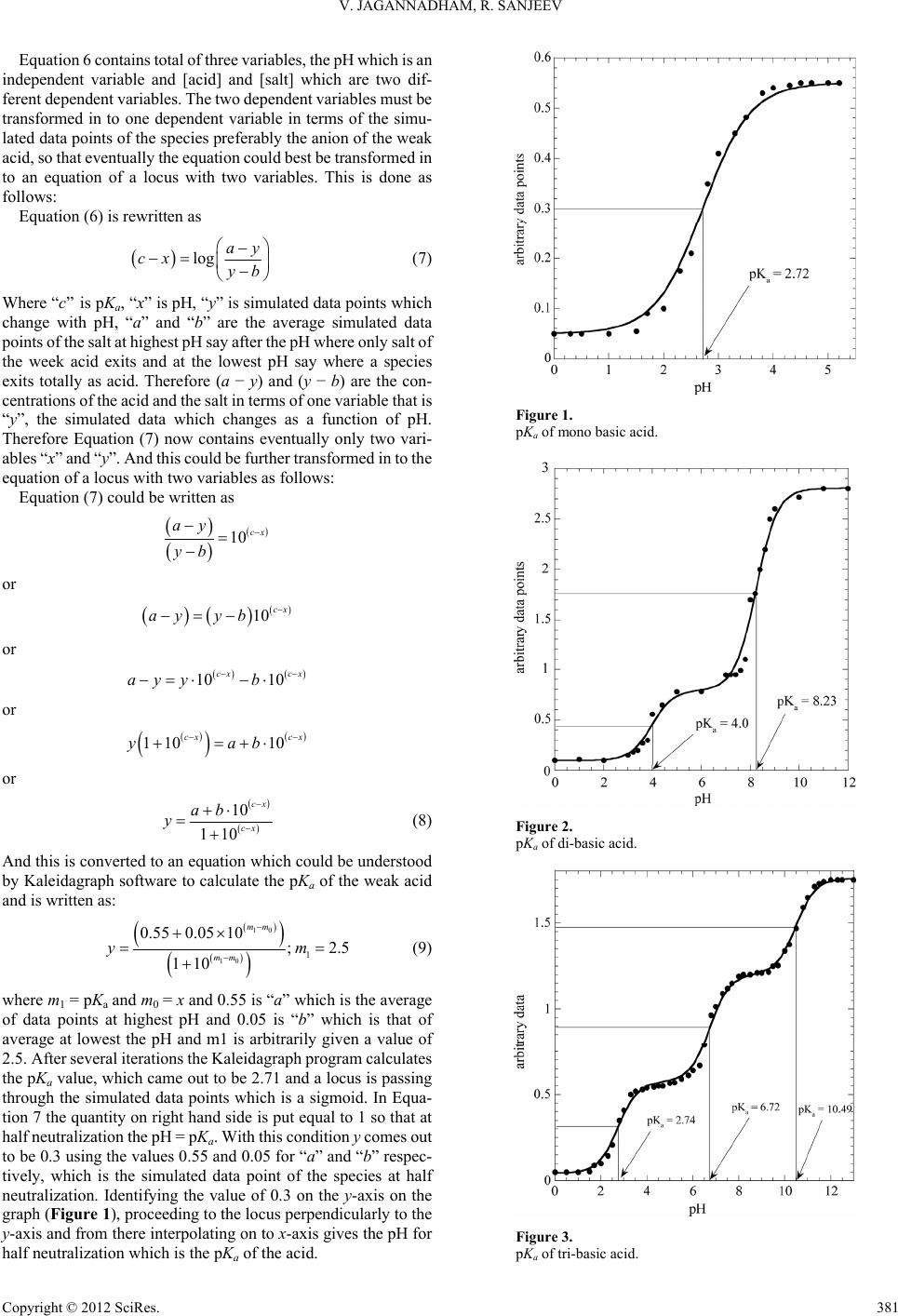

V. JAGANNADHAM, R. SANJEEV
Equation 6 contains total of three variables, the pH which is an
independent variable and [acid] and [salt] which are two dif-
ferent dependent variables. The two dependent variables must be
transformed in to one dependent variable in terms of the simu-
lated data points of the species preferably the anion of the weak
acid, so that eventually the equation could best be transformed in
to an equation of a locus with two variables. This is done as
follows:
Equation (6) is rewritten as

log ay cx yb
 
 



(7)
Where “c” is pKa, “x” is pH, “y” is simulated data points which
change with pH, “a” and “b” are the average simulated data
points of the salt at highest pH say after the pH where only salt of
the week acid exits and at the lowest pH say where a species
exits totally as acid. Therefore (a − y) and (y − b) are the con-
centrations of the acid and the salt in terms of one variable that is
“y”, the simulated data which changes as a function of pH.
Therefore Equation (7) now contains eventually only two vari-
ables “x” and “y”. And this could be further transformed in to the
equation of a locus with two variables as follows:
Equation (7) could be written as




10 cx
ay
yb



or





10 cx ayyb  
or
 
10 10
cx cx
bayy  
or



1110 0
cx cx
yab


or


10
101
cx
cx
ab
y


 (8)
And this is converted to an equation which could be understood
by Kaleidagraph software to calculate the pKa of the weak acid
and is written as:





10
10 1
0.550.05 10
;2.
110
mm
mm
ym




5 (9)
where m1 = pKa and m0 = x and 0.55 is “a” which is the average
of data points at highest pH and 0.05 is “b” which is that of
average at lowest the pH and m1 is arbitrarily given a value of
2.5. After several iterations the Kaleidagraph program calculates
the pKa value, which came out to be 2.71 and a locus is passing
through the simulated data points which is a sigmoid. In Equa-
tion 7 the quantity on right hand side is put equal to 1 so that at
half neutralization the pH = pKa. With this condition y comes out
to be 0.3 using the values 0.55 and 0.05 for “a” and “b” respec-
tively, which is the simulated data point of the species at half
neutralization. Identifying the value of 0.3 on the y-axis on the
graph (Figure 1), proceeding to the locus perpendicularly to the
y-axis and from there interpolating on to x-axis gives the pH for
half neutralization which is the pKa of the acid.
Figure 1.
pKa of mono basic acid.
Figure 2.
pKa of di-basic acid.
Figure 3.
pKa of tri-basic acid.

V. JAGANNADHAM, R. SANJEEV
382
Hence, the “Kaleidagraph” software is a “Hands On” tool for
any graduate program laboratory.
Similarly the following equations were derived and used for di
and tri-basic acids respectively:




12
1
112 2
10 10
110 110
cx cx
cx cx
ab ab
y




2

(10) REFERENCES
Brunton, L. L., Lazo, J. S., & Parker, K. L. (2006). Las bases farmaco-
lógicas de la terapéutica. Spain: McGraw Hill.






3
12
12
112 23 3
1010 10
110110 110
cx cx cx
cxcx cx
abab ab
y

 


 

3
(11)
Devlin, T. (2003). Bioquímica. Barcelona: Reverté.
Guyton, A. C. (2006). Tratado de Fisiol o g í a Médica. Spain: Elsevier.
where, a1, a2, a3, b1, b2, b3, c1, c2, and c3 have their usual sig-
nificance analogous to Equation (8). Accordingly they were fit
for the data and Figures 2 and 3 were obtained.
Stryer, L. (2003). Biochemistry. Barcelona: Reverté.