Paper Menu >>
Journal Menu >>
 J. Software Engineering & Applications, 2010, 3, 603-609 doi:10.4236/jsea.2010.36070 Published Online June 2010 (http://www.SciRP.org/journal/jsea) Copyright © 2010 SciRes. JSEA Dynamic Two-phase Truncated Rayleigh Model for Release Date Prediction of Software Lianfen Qian1, Qingchuan Yao2, Taghi M. Khoshgoftaar2 1Department of Mathematical Sciences, Florida Atlantic University, Boca Raton, USA; 2Department of Computer Science and Engineering, Florida Atlantic University, Boca Raton, USA. Email: lqian@fau.edu, qingchuan_yao@yahoo.com, taghi@cse.fau.edu Received October 23rd, 2009; revised November 13th, 2009; accepted November 15th, 2009. ABSTRACT Software reliability modeling and prediction are important issues during software development, especially when one has to reach a desired reliability prior to software release. Various techniques, both static and dynamic, are used for reliability modeling and prediction in the context of software risk management. The single-phase Rayleigh model is a dynamic reliability model; however, it is not suitable for software release date prediction. We propose a new multi-phase truncated Rayleigh model and obtain parameter estimation using the nonlinear least squares method. The proposed model has been successfully tested in a large software company for several software projects. It is shown that the two-phase truncated Rayleigh model outperforms the traditional single-phase Rayleigh model in modeling weekly software defect arrival data. The model is useful for project management in planning release times and defect management. Keywords: Software Testing, Weekly Defect Arrival Data, Single-Phase Rayleigh Model, Two-Phase Truncated Rayleigh Model, Software Reliability 1. Introduction Software reliability is a key attribute of software qual- ity. Various models have been developed for software reliability engineering [1]. The rising complexity, size and functionality of software systems make software reliabil- ity prediction difficult. The problem is compounded with short development times and strict release deadlines. Consequently, predicting the release date for achieving pre-specified system reliability has become a very im- portant issue in software project development. Reliability modeling can not only assist in fulfilling commitments and project deadlines, but also aid in efficient resource management and planning. Software reliability is the probability of failure-free software operation for a given period of time in a given operating environment. The key attribute in software reliability engineering is the number of defects observed in specified time intervals (e.g. weeks). Software reli- ability prediction models assess a software product’s reliability or estimate the number of latent defects when it is released to the customers. Such an estimate is important for two reasons: 1) as an objective statement of the quality of the product and 2) for resource planning in the software maintenance phase. There are two categories of software reliability models: static and dynamic models. Among the static models, Bayesian belief networks [2] and utilizing software pro- cess metrics are relatively popular. Related literature also proposes various models for software defect prediction which can be used to indirectly gauge software reliability [3,4]. The primary drawback among static models can not effectively capture the software process and its variations during the course of software project development. On the other hand, a dynamic software reliability model is re- flective of the software testing phase and is generally applicable before product release. Among dynamic models, the (single-phase) Rayleigh model has been shown suitable to fit software defect ar- rival patterns [5,6]. A single-phase Rayleigh model di- vides the whole software development life cycle into six stages that are in chronological order: High Level Design (HLD), Low Level Design (LLD), CODING, Unit Test- ing (UT), Integration Testing (IT) and System Testing (ST). The six stages are assigned to a sequence of nu- merical scales. That is: HLD = 0.5, LLD = 1.5, CODING = 2.5, UT = 3.5, IT = 4.5 and ST = 5.5 [5]. Those nu- merical assignments seem rather ad hoc. Instead, we  Dynamic Two-Phase Truncated Rayleigh Model for Release Date Prediction of Software 604 could assign the six stages to, for instance, {t1, t2, t3, t4, t5, t6}, as long as satisfies t1 < t2 < t3 < t4 < t5 < t6. With different numerical assignments for the six stages, the fitted single-phase Rayleigh models could show a much different accuracy pattern, as shown in Figure 1. 6 1 ii t The defects/KLOC in Figure 1 is reconstructed from the work of Thangarajan et al. [5]. The quadratic fit is shown to illustrate that the small pairs of data could be fitted well by an arbitrary model such as quadratic model, rather than just single-phase Rayleigh model. Also, by assigning one numerical number to each stage, the data set now contain only six pairs at most. For prediction pur- poses, most likely 3, 4 and 5 pairs available, such a small sample size offers no confidence in the reliability predic- tion. During the software development life cycle, collecting one single representative number for each stage results in a very small sample size. Furthermore, it is more likely that the data of major software defects are followed week- ly, hence allowing project management to monitor the dynamic progress of the software development process. Our motivated weekly software development defects data set, Figure 2, shows the serious inadequacy of the sin- gle-phase Rayleigh model. This leads to our research on developing a better dynamic software reliability model to estimate the number of major defects, hence predict soft- ware release date. The existing organizational reliability prediction model for software release date prediction at a large software company, where the weekly data in Figure 2 were col- lected, is the dynamic single-phase Rayleigh model [5,6]. The software process in the organization consisted of two or more development phases. This is due to the software production cycles, availability of supporting hardware (e.g. wingboard/test phones) in the earlier software de- velopment stages, man-power management (e.g. testers’ rearrangement) during the software development phases, and other dynamic issues during development. Figure 2, for instance, shows that the scatter plot overlaid with the single and the newly proposed two-phase truncated (piecewise, for short) Rayleigh models for the data set from the large software company. It is clear that the two-phase truncated Rayleigh model fits the data much better than the single-phase Rayleigh model. Motivated by the example, we propose a multiple- phase truncated Rayleigh model in this paper. Such a model is better suited to fit the weekly defect arrival pat- terns during software development process. For simplicity reasons, we focus on the two-phase truncated (piecewise) Rayleigh model. The model can be extended to include additional phases reflecting the development process. It is shown through empirical modeling that the model accu- racy is significantly improved. Furthermore, using the two-phase truncated Rayleigh model, the release date is predicted with a much higher confidence level. The paper is organized as follows: Section 2 summa- rizes the single-phase Rayleigh model and proposes the multi-phase model, with a focus on the two-phase trun- cated Rayleigh model. Section 3 presents the algorithms of nonlinear least squares estimators of the model pa- rameters and flowcharts of the dynamic process. Section 4 applies the proposed two-phase truncated Rayleigh model to defect arrival data of a large real-world software project from the large software organization. Finally, Section 5 concludes the paper and provides suggestions for future work. 2. Multi-Phase Truncated Rayleigh Models for Software Reliability Prediction The dynamic single-phase Rayleigh model is a standard technique for software reliability modeling, and has been widely used for the software project and quality man- agement in the software industry. The software organiza- tion, from which our case study data is obtained, has uti- lized the dynamic single-phase Rayleigh model for sev- eral of their previous software project developments. The single-phase Rayleigh model is a parametric re- gression model with the regression function specified by the Rayleigh distribution with a multiplier coefficient. When the parameters of the Rayleigh distribution are estimated based on the updated data from a software project, dynamic projections about the number of defects for the software can be made based on the model over the software development life cycle. The Rayleigh distribution is a special case of Weibull distribution, and has various applications including reli- ability estimation and life cycle pattern modeling [7,8] in developing software projects, life testing experiments in clinical studies dealing with cancer patients [9]. We now summarize the Rayleigh distribution. Denote tm be the time at which the single-phase Rayleigh density curve reaches its peak. The cumulative distribution function of Rayleigh distribution with the constant multiplier K (the total number of latent defects) is 2 (;, )1, t FtKK e where =1/(2tm 2) is the scale parameter. The single-phase Rayleigh model has a regression function parameterized as, 2 (;, )2t f tKK te (1) where both K and are the two parameters that need to be estimated using the data. The single-phase Rayleigh model (1) does not fit the Copyright © 2010 SciRes. JSEA 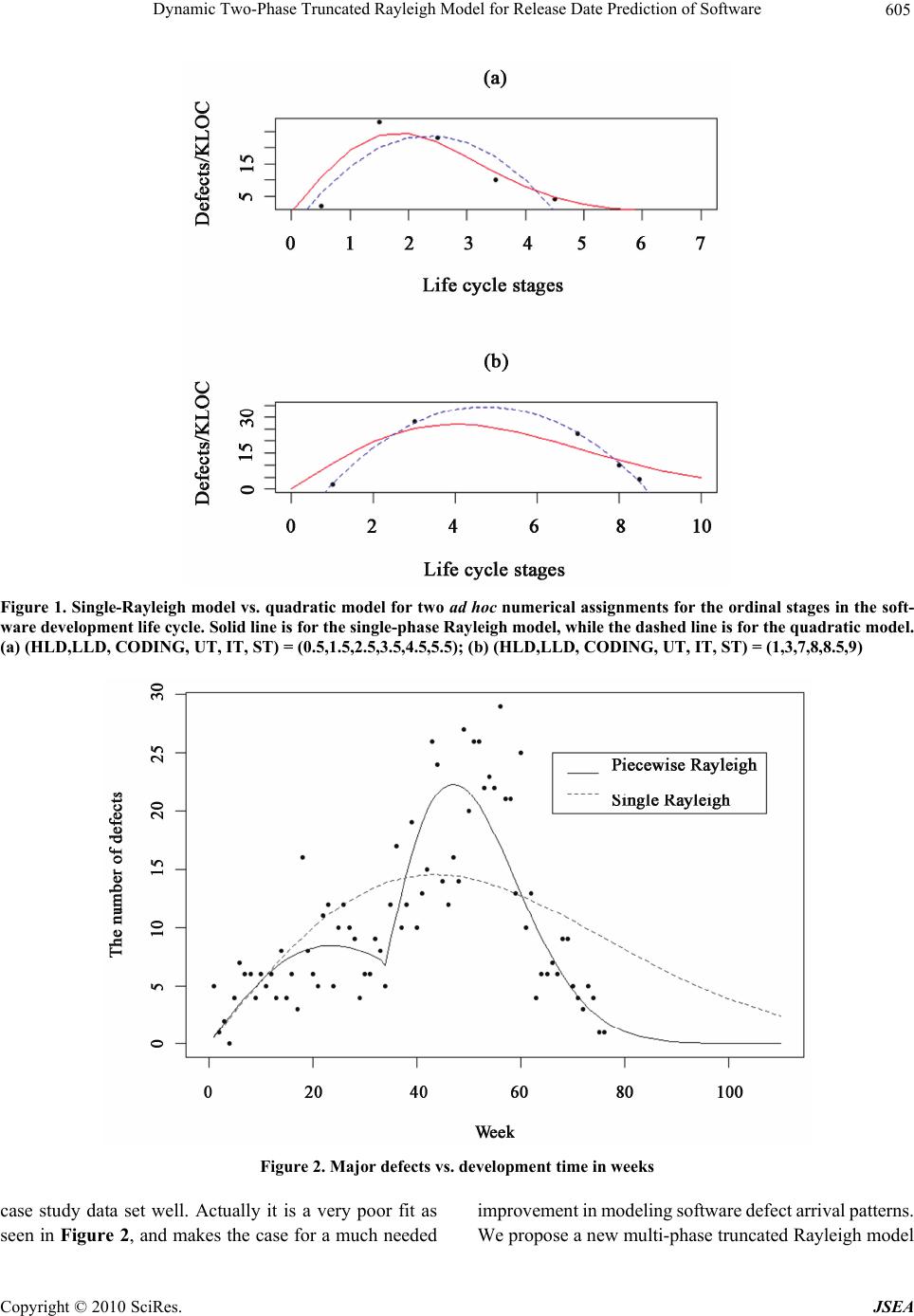 Dynamic Two-Phase Truncated Rayleigh Model for Release Date Prediction of Software Copyright © 2010 SciRes. JSEA 605 Figure 1. Single-Rayleigh model vs. quadratic model for two ad hoc numerical assignments for the ordinal stages in the soft- ware development life cycle. Solid line is for the single-phase Rayleigh model, while the dashed line is for the quadratic model. (a) (HLD,LLD, CODING, UT, IT, ST) = (0.5,1.5,2.5,3.5,4.5,5.5); (b) (HLD,LLD, CODING, UT, IT, ST) = (1,3,7,8,8.5,9) Figure 2. Major defects vs. development time in weeks case study data set well. Actually it is a very poor fit as seen in Figure 2, and makes the case for a much needed improvement in modeling software defect arrival patterns. We propose a new multi-phase truncated Rayleigh model  Dynamic Two-Phase Truncated Rayleigh Model for Release Date Prediction of Software 606 , , defined as below: 11 1 1221 12 111 (;,), 0 (;,), (; ) (;,), ddd dd ftK t ft Kt gt ft Kt where d is the number of phases and T=( 1,…, d, K1,…, Kd, 1,…, d-1, 1,…, d-1) is the model parameter vector. For simplicity, we will discuss the case with d = 2, the two-phase truncated (piecewise) Rayleigh model with regression function parameterized as follows: 11 22 (;,), 0 (; )(;,), ftK t gt f tK t (2) where is the location of the phase change, is the starting location for the second phase. Due to the nature of the software defect data, we suggest to use the left trun- cated Rayleigh model for the second phase. Then T = ( 1, 2, K1, K2, , ) is the parameter vector, need to be esti- mated. 3. Algorithms for Piecewise Rayleigh Models In this section, we describe the nonlinear least squares estimator of the model parameters. Let 1 (, ) n ii i td be the defect arrival data collected over time, where /n i ti is the time index for the ith week, is the total number of software defects detected during the ith week, and n is the number of weeks observed. Let i d 2 1 () (;). n ii i Sdgt Then the nonlinear least squares estimator is the mi- nimization of S(). Notice that S() is not differentiable in the location of phase change point and the starting point of second phase . In conjunction with nonlinear least squares method and Gauss-Newton algorithm, we utilize a four-step technique (described below) to obtain the estimators of the parameter vector . The package nls in R language is used to obtain the estimates of the model parameters. Step 1: For any given location of phase change in (0, 1), fix a such as 0 < < 1, we compute the nonlinear least squares estimators [10],1(,) n 2 ) for the smooth parameters 1121 (, ,, T K K , by minimizing S( ) over 1. Step 2: Substitute 1(,) n (,S into S( ) to obtain the profile objective function, ) . Then we minimize (,)S over 0 < < 1 for the given to obtain() . Notice that the minimizer () is a function of . Step 3: Substitute () into (,)S to get ()S . The minimizer of ()S over (0, 1) is called the change point estimator, denoted byˆ . Step 4: Substituteˆ into() to get ˆ and 1ˆˆ , n to get1 ˆn . Put them together, we obtain the nonlinear least squares estimator, ˆ 1 ˆ ˆ ,, T n ˆ T n of . Figures 3 and 4 illustrate the flow charts of the dy- namic process of the algorithm for single-phase and mul- ti-phase truncated Rayleigh models, respectively. We pro- vide the flowchart for the single-phase Rayleigh model for comparison purpose. 4. Application to a Real Software Defect Data Set The data set motivated our research were collected from Feb-25-06 to Aug-04-07 at a large software company. There are 76 weeks software defects arrival data. Number of major defects during a week is reported. 4.1 Single-phase vs. Piecewise Rayleigh Models We illustrate the two-phase truncated Rayleigh model by fitting the software defect arrival data set. From Figure 2, it is observed that using two-phase truncated Rayleigh model improves the model fitting significantly compared to the single-phase Rayleigh model with respect to model accuracy and model goodness-of-fit. For comparison Figure 3. Algorithm for single-phase Rayleigh model Copyright © 2010 SciRes. JSEA  Dynamic Two-Phase Truncated Rayleigh Model for Release Date Prediction of Software Copyright © 2010 SciRes. JSEA 607 Figure 4. Algorithm for multi-phase Rayleigh model purpose, the estimated single-phase Rayleigh regression function is given by, 2 ˆ ˆ ˆ ˆ() 2, t gtK te where and ˆ13.7111 Kˆ1.5297. For the two-phase truncated Rayleigh model (2), the estimated change is at the ˆ = 33rd week with the starting point estimated at ˆ = 31st week for the second phase. Hence phase one is from the first week to 33rd week and phase two is from the 34th week to the 76th week with estimated starting point at ˆ = 31st week. The estimated first phase (right truncated) of the regres- sion function is estimated as 2 2 ˆ( 31/76) 22 ˆ ˆ ˆ()2(31/76), t gtK te if 33 / 76,t with and the second phase (left truncated) of the regression function is estimated 11 ˆ ˆ4.3022, 5.2279,K as 2 2 ˆ( 31/76) 22 ˆ ˆ ˆ()2(31/76), t gtK te if 33 /76,t with . Figure 2 shows the scatter plot overlaid with the two fitted curves using the single-phase and two-phase truncated Rayleigh models, respectively. From the fitted model, one can predict the future week’s number of software defects and establish the quality assurance criterion and management for pre- dicting the release date. 22 ˆ ˆ7.7731, 11.2445K This proposed multi-phase truncated Rayleigh model can be utilized for modeling any future software devel- opment projects to obtain better prediction and provide more efficient estimation of the release date of the soft- ware product. 4.2 Quality Assurance Criterion for Release Date Prediction In this section, we establish the quality assurance crite- rion for software release. The quality assurance criterion is determined by 95% and 99.9% confidence levels. That is, based on the fitted model, if the model shows that 95% or 99.9% of the total expected software defects has been detected, then we suggest that the software is ready for release. For the single-phase Rayleigh model, we estimate the release date with 95% confidence level. We set ˆ ˆ ; ,0.95FtK K ˆ and solve for t or equivalently 2 ˆ 1 0.95. t e This implies that the release date equals to the ceiling of ˆ ln(1.95)107 weeks,n where Hence, with 95% confidence the software project will ˆ=1.5297.  Dynamic Two-Phase Truncated Rayleigh Model for Release Date Prediction of Software 608 need 107−76 = 31 weeks of further testing before releas- ing the software product. That is the predicted release date using the 76 weeks of data is Feb-29-08 based on the single-phase Rayleigh Model. With 99% confidence, it will require even much longer testing time. Alternatively, utilizing the two-phase truncated Ray- leigh model (2), we set ˆ// 1 ˆ 0/ 0 ˆˆ ˆ ()()0.999 () nin n g tdt gtdtgtdt and solve for i to get the estimated release week with 99.9% confidence level. Equivalently, the estimated re- lease week number, i, satisfies that ˆ 1/ 22 ˆˆ ˆ ˆˆ 22 00 2 1 0 2 ˆˆ 0.999()( ) ˆ 0.999 , ˆ n i nn g tdt gtdt ee K AA AK (3) where 2 ˆ ˆ ˆ2 0 ˆ/ 10 1 0 0.9922, ˆ( )2.6967, ˆ( )10.2586. n n Ae Agtdt Agtdt Solving Equation (3) to obtain the estimated release week number: 1 20 2 0.999 ˆ ˆ1/ln76 weeks, ˆ AA in AK where {x} is the smallest integer greater or equal to x. This indicates that with 99.9% confidence that the esti- mated release week is the end of 76th week. That is the software is ready for release, with almost 100% confi- dence based on the two-phase truncated Rayleigh model. We note that the large software organization has adopted our new two-phase truncated Rayleigh model and is us- ing it to predict the number of software defects dynami- cally and release dates for ongoing software projects. Our new two-phase truncated Rayleigh model has im- proved the software release life cycle a great deal and has saved a lot of man-powered resource for the large software organization. 4.3 Model Performance Check We utilize three measures of goodness-of-fit to assess the performance of the models: root mean square error (RMSE), magnitude of relative error (MRE), and ad- justed coefficient of determination 2 adj R . The root mean square error measures the model accuracy defined as the square root of mean squared residuals. That is, 2 1 1ˆ, 5 n ii i RMSEd d n where di is the number of defects detected during the ith week, is the fitted (predicted) value of di. The smaller the RMSE, the better the model fits. ˆi d The second criterion for assessment of the perform- ance of model fitting used in the reliability literature is the mean magnitude of relative error, defined as 1 1 ˆ (0) . (0) n ii i ii n i i dd Id d MRE Id The implicit assumption in this summary measure is that the seriousness of the absolute error is proportional to the size of the observations. The smaller the MRE, the better the model fits. The third measure of goodness-of-fit used is the ad- justed determination of coefficient which is the adjusted percentage of variation in the number of defects per week explained by the model. That is 2 adj R 2/(5) 1, /( 1) adj SSE n RSSTO n where SSE = (n-5)(RMSE)2 and 21 1 with . n ni i i i d SSTOd ddn The higher of the , the better the model fits. 2 adj R Table 1 summarizes the three performance criteria for the real-world weekly software defects data set using both single-phase and two-phase truncated (piecewise) Rayleigh models. Based on the reported RMSE, MRE and values, the two-phase truncated Rayleigh mo- del is much better than the single-phase Rayleigh model. The MRE is reduced by about 50%, while the good- ness-of-fit measure is roughly doubled for the two- phase truncated compared to the single-phase Rayleigh models. The two-phase truncated Rayleigh model ex- plains the almost doubled variation in the number of de- fects than the single-phase Rayleigh model does. Thus, based on the given data, we conclude that the two-phase truncated Rayleigh model is an attractive model for pre- dicting weekly software defects and release date of soft- ware projects. 2 adj R 2 adj R Copyright © 2010 SciRes. JSEA  Dynamic Two-Phase Truncated Rayleigh Model for Release Date Prediction of Software Copyright © 2010 SciRes. JSEA 609 REFERENCES Table 1. Model comparisons using RMSE, MRE and 2 adj R Criterion Model RMSE MRE 2 adj R Single-phase 5.97 0.76 36.6% Two-phase 4.13 0.36 70.4% [1] M. R. Lyu, “Software Reliability: To Use or not to Use?” Proceedings of 5th International Symposium on Soft- ware Reliability Engineering, 66-73 November 1994. [2] Y. Wang and M. Smith, “Release Date Prediction for Telecommunication Software Using Bayesian Belief Networks,” Proceedings of the 2002 IEEE Canadian Conference on Electrical and Computer Engineering, 2002, pp. 738-742. 5. Conclusions [3] T. M. Khoshgoftaar and N. Seliya, “Fault Prediction Modeling for Software Quality Estimation: Comparing Commonly Used Techniques,” Empirical Software Engineering Journal, Vol. 8, No. 3, 2003, pp. 255-283. The research was motivated by a real-world software defect arrival data over many weeks from a large software organization. The paper proposes a new multi-phase truncated (focusing on a two-phase truncated model) Ray- leigh model in fitting weekly defect arrival data. [4] T. M. Khoshgoftaar and N. Seliya, “Comparative Asse- ssment of Software Quality Classification Techniques: An Empirical Case Study,” Empirical Software Engin- eering Journal, Vol. 9, No. 3, 2004, pp. 229-257. It is shown that the proposed model is much more ac- curate than the existing single-phase Rayleigh model. The single-phase model was previously used by the organiza- tion during software development. Using both MRE and performance measures, the proposed model almost doubled the prediction accuracy, hence, shortening the release date prediction with a higher confidence level. From a software reliability perspective, our proposed two-phase truncated Rayleigh prediction model will help in the management and planning of project resources toward bettering the software release cycle time. 2 adj R [5] M. Thangarajan and B. Biswas, “Mathematical Model for Defect Prediction across Software Development Life Cycle,” The SEPG (Software Engineering Process Group) Conference, India, 2000. http://www.qaiindia. com/Conferences/SEPG2000/index.html [6] S. H. Kan, “Metric and Models in Software Quality Engineering,” 2nd Edition, Addison Wesley, Massa- chusetts, 2003. [7] P. V. Norden, “Useful Tools for Project Management,” Operations Research in Research and Development, B. V. Dean, Ed., John Wiley & Sons, New York, 1963. The two-phase truncated Rayleigh model can be easily extended to a multi-phase truncated Rayleigh model. Hence it can be used to predict release date for future software projects with a higher confidence level. A general multi-phase Rayleigh software release prediction model can be developed to automatically detect and reflect all the change locations and the starting points of the software development phases so that the multiple-phase truncated Rayleigh software prediction model can be generated to automatically forecast the software release time. [8] L. H. Putman, “A General Empirical Solution to the Macro Software Sizing and Estimating Problem,” IEEE Transaction on Software Engineering, Vol. SE-4, 1978, pp. 345-361. [9] S. K. Bhattacharya and R. K. Tyagi, “Bayesian Survival Analysis Based on the Rayleigh Model,” Trabajos de Estadistica, Vol. 5, No. 1, 1990, pp. 81-92. [10] D. M. Bates and J. M. Chambers, “Nonlinear Models,” Chapter 10 of Statistical Models in S. J. M. Chambers and T. J. Hastie, Eds., Wadsworth & Brooks/Cole, 1992. |

