J. Software Engineering & Applications, 2010, 3, 548-555
doi:10.4236/jsea.2010.36063 Published Online June 2010 (http://www.SciRP.org/journal/jsea)
Tabu Search Solution for Resource Confidence
Considered Partner Selection Problem in
Cross-Enterprise Project
Hanchuan Xu, Xiaofei Xu, Ting He
School of Computer Science & Technology, Harbin Institute of Technology, Harbin, China.
Received April 1st, 2010; revised April 21st, 2010; accepted April 23rd, 2010.
ABSTRACT
Cross-enterprise project is the main implementation form in multi enterprises collaborative production environment.
Minimizing the risk of failure and tardiness caused by the uncertainty of partner’s resources in partner selection is the key
problem to ensure success in Cross-enterprise project. In this paper
, considering the factors and constraints of
sub-project processing times, precedence of sub-project and project due date, especially the resource confidence, a 0-1
integer programming model was presented with the objective to minimize the risk of failure and the tardiness of the
project. A project scheduling algorithm was designed to search and evaluate selection solutions, and the project
scheduling algorithm was embedded into a Tabu search algorithm to solve the model. Simulation experiments and
comparisons with other algorithms showed that the proposed approach was possible to find the optimal solution with a
faster speed and higher probability.
Keywords: Cross-Enterprise Project, Partner Selection, Resource Confidence, Tabu Search
1. Introduction
To be competitive in the global manufacturing environ-
ment with the rapidly increasing competitiveness, strate-
gic collaborations between enterprises are needed in order
to meet the market’s requirements for quality, respon-
siveness, and customer satisfaction. Dynamic alliance,
virtual enterprise, extended enterprise, and supply chain
are the major management philosophies for multi enter-
prises collaborative production environment.
Cross-enterprise project (CEP) management pattern arose
as the main implementation form in these management
philosophies. CEP is the formation of closer co-ordination
in the design, development, costing and the co-ordination
of the respective manufacturing schedules of co-operating
independent manufacturing enterprises and related sup-
pliers [1,2]. There are four stages in CEP life cycle: for-
mation, operation, evolution and dissolution. A major
issue in the formation phase is to select appropriate part-
ners and allocate tasks between partners. During this
process, the core enterprise comprehensively evaluates
partners according to cost, quality, credit, delivery time,
etc., and then based on certain criteria, find the best
combination of partners to collaborate to complete the
project.
Partner selection has attracted much research attention
recently, because it is an important function for informa-
tion management systems, such as project management
(PM), enterprise resource planning (ERP) and supply
chain management (SCM). Most of researches about the
partner selection problem are based on qualitative analysis
methods. However, quantitative analysis methods for
partner selection are still insufficient. Many operation
research methods, such as analytic hierarchy process
(AHP), analytic network process (ANP) and fuzzy syn-
thetic evaluation are widely used to the problem, but
mathematical models and optimization methods for part-
ner selection are still a challenge [3,4]. In partner selection
process, although there are many factors needed to be
considered such as friendship, credit, quality, and reli-
ability, the cost and completion time are the two key
factors and focused on by most researchers.
In CEP, the resources belong to different partners
which often undertake other projects at the same time, so
the available production capacity of partner will be tight
during some periods. In addition, unforeseen exceptions
also inevitably occur. All of these make resources have a
certain degree of uncertainty. Although there are some

Tabu Search Solution for Resource Confidence Considered Partner Selection Problem in Cross-Enterprise Project 549
constraints between enterprises such as contracts, the case
that partners can’t provide promised resources on time or
in right quality is not able to be completely avoided. When
this happens, it will seriously affect the production sche-
dule of core enterprise and even cause the whole cross-
enterprise project failed. So the confidence level of re-
source that can be provided by partners on time and in
right quality which we defined as resource confidence is a
very important factor in the partner selection problem.
However, most researchers mainly take into account the
cost and completion time, and the objective is to minimize
the total cost of the project or the project duration. The
factor of resource confidence is neglected in most re-
searches.
Yannis and Andreas [5], Sha and Che [6], Mikhailov [7]
and other researchers proposed some models and ap-
proaches for partner selection by establishing a CEP,
where cost, time and distance were considered. However,
the other two important factors, the resource confidence
and the precedence of sub-project, were not considered in
their papers. As Wang et al. [8] indicates, in the coopera-
tion relationship of sub-projects contracted by partners, it
may be represented by an activity network with prece-
dence. Thus, the problem could be considered as a partner
selection problem embedded with project scheduling.
Naiqi et al. [9] considered the completion time as a con-
straint and modeled the partner selection problem by an
integer programming formulation to minimize the manu-
facturing cost. The formulation was then transformed into
a graph-theoretical formulation and a 2-phase algorithm
was developed to solve the problem. Wang et al. [8] took
into consideration the factors of cost, completion time and
precedence of sub-project, described the partner selection
problem with a 0-1 integer programming formulation to
minimize the total cost of the project. They then devel-
oped a fuzzy decision embedded heuristic genetic algo-
rithm to find the solution for partner selection. The ex-
periments showed that the algorithm was possible to
quickly achieve optimal solution for large size problems.
Taking into account the same factors and objective as
Wang [8], W. H. IP et al. [10] and Zhibin et al. [11] sepa-
rately proposed branch and bound solutions for partner
selection problem in virtual enterprises and their solutions
were especially effective to medium or small size prob-
lems. In all these papers mentioned above, their objectives
were minimizing the total cost of project and didn’t con-
sider the impact of resource confidence to project im-
plementation risk. To minimize risk in partner selection
and ensure the due date of a project in virtual enterprise,
W. H. IP et al. [12] described and modeled a risk-based
partner selection problem. They developed a rule-based
genetic algorithm with embedded project scheduling to
solve the problem. In their paper, they assumed that each
candidate partner had a fail probability of its contracted
sub-project. In fact, the fail probability of the sub-project
closely related to whether the partner’s available re-
sources were tight or not in the duration of the sub-project.
The tighter the resources are, the higher the fail probabil-
ity is, and vice versa. However, the production load of
partner is varied in different periods, so the available
resource and fail probability are also different. They used
a whole fail probability for all periods and didn’t consider
the difference of fail probability in different periods.
To solve the partner selection problem in CEP, we first
describe it with a 0-1 integer programming model con-
sidering the factors of process time, precedence of sub-
projects, and resource confidence. Then a project sched-
uling algorithm is proposed to calculate the project com-
pletion time and the time window of each sub-project
under a feasible solution. From this, we embed the project
scheduling algorithm into a Tabu search algorithm to
obtain the optimal partner selection solution. The com-
putation results showed that the proposed approach is
efficient to achieve the optimal solution.
The paper is structured as follows. In Section 2 the
problem and the model are introduced. Then the solution
space reduction method and the project scheduling algo-
rithm to evaluate selection solution are presented in Sec-
tion 3. The Tabu search algorithm embedded the project
scheduling is presented in Section 4. Section 5 reports an
experimental example and computational results obtained
by testing the algorithm on some test instances. Finally,
Section 6 presents our overall conclusions.
2. Model for Partner Selection Considering
Resource Confidence
The problem of partner selection for CEP considering
resource confidence can be described as follows:
Assuming an enterprise (core enterprise) obtain a big
project consisting of several sub-projects. It is not able to
complete the big project by itself from its own resources
and has to find some partner enterprises to collaboratively
finish the project. The partner selection procedure is di-
vided into two phases. Firstly, the enterprise determines
the payment and some basic requirements for the process
time and quality of each sub-project. The partners who
can accept the conditions will propose the process time
they need to finish the sub-project according to their own
capacity. They constitute the candidate partner set. In the
second phase, the enterprise comprehensively evaluates
all candidates and calculates the confidence of resource
provided by the partner for the sub-project. At last the
enterprise selects the most appropriate partner for each
sub-project. There exists plenty methods to evaluate the
individual candidate partner and calculate the resource
confidence, for an extensive review we refer to MALONI
and BENTON [3] and BOER et al. [4]. In this paper, we
just focus on the second phase, i.e., how to select partners
according to the resource confidence.
Based on the risk-based partner selection model pre-

Tabu Search Solution for Resource Confidence Considered Partner Selection Problem in Cross-Enterprise Project 550
sented by W. H. IP et al. [12] and considering the resource
confidence, we present a 0-1 integer programming model
MPCPS for the partner selection problem. Suppose that
the project consists of sub-projects, there are prece-
dence relationship between these sub-projects and they
form a precedence activity network
n
H
. If sub-project
can only begin after the completion of sub-project , we
call sub-project as the immediate predecessor of sub-
project and define the connected sub-project pair
by . For the convenience of description, we
label these sub-projects such thik. Without the loss
of generality, the final sub-project is labeled as sub-pro-
ct n. Thus, we can define that the completion time of
final sub-proct n c is the completion time of the project.
Each sub-project has some candidate partners, for sub-
1, 2,..., n
, the are i
m candidate partners,
and for the candidatener
k
i
i
k

i,
,ik H
j
project 
at
je
e
re
i
part
j
of su-project i, its
processing times is ij qperiods. The resource confidence
candidate
b
of
j
to ub-project in period t isd as
()
ij
dt () (0,1]
ij
dt. The due date of the project is
D. To simplify the problem, we assume that the core en-
terprise will select only one candidate to undertake one
sub-project.
si note
and there
The objective is to select the optimal combination of
partners for all sub-projects in order to maximize the
whole resource confidence of the project and to finish the
project within the due date.
The following decision variable is defined.
1
() 0
ij
xt  

Then the problem can be modeled as follows:
MPCPS
 




 n
i
m
j
c
t
*
n
qt
tτ
ij
ij
ijd
x
in ij
Dcβτd
q
txxFmax
111
1
)]][[(1])(
1
)[()(
(1)
s.t.
11
()1;1, 2,...,
mc
in
ij
jt
x
ti


 n

(4)
(2)
11 11
()( )( );1,2,...,,,
mcm c
in kn
ij ijkjn
jt jt
tqxttxttcikH
 

 
(3)
11
()()
mc
nn
nj njn
jt
tqxt c



(){0,1}, ,
ij
x
tijt (5)
where []
x
stands for },0 w,[]
{max
y
stands for
min{1, d }y an

is the tardencoefficient.
(1) is the objective function, where
iness palty
Formula 1
i
j
q
.
1tq
ij ()
ij
td



ence for candidate


source confid
is the mathematical expectation of re-
j
of sub-project i in
the ij
q continuous periods, and bbreviated as ij
a
E
bel-
low.onstraint (2) ensures that each sub-project will be
contracted to only one partner and constraint (3) is the
precedence constraint of sub-projects. Constraint (4)
gives the method to calculate the completion time of the
project.
It is ob
C
vious []
y

ar
at
o
e
ion
mp
that the operator []
x
and non-
ot c
PCPS is a clex
an
3.1
alytical and the objective function is nontinuous
and differentiable, so it is difficult to treat the model by
traditional mathematical programming methods. There-
fore, we develop a project scheduling embedded Tabu
search (PSTS) algorithm to solve this problem.
3. Solution Space Reduction and Evalu
Algorithm of Solution
Solution Space Reduction
MThe partner selection modeled as
combinatorial optimization problem. The number of fea-
sible solutions (solution space) is very large, even for a
small-scale problem. To simplify the solving process, W.
H. IP et al. [12] defined the concept of inefficient candi-
date and proved that the optimal solution consists without
any inefficient candidate. To efficiently reduce the solu-
tion space, all inefficient candidates can be ignored in the
solving process without losing the optimal solution. Based
on the definition presented by W. H. IP [12] and consid-
ering the characteristics of the model MPCPS, we define
the inefficient candidate to our model as follows.
Definition 1. For the two candidates
j
and k o
candidate j is selected to sub-project i at period t
otherwise
f sub-
pr
,d
oject i, if min max [, ]
ii
tES LF min max
[, ]
ii
tESLF ,
()
ikij ik
qq t()
ij
dt

n , or ik ,(
ik
d)t()t
ij
qq ij d, the
the candidate
j
is called inefficient candidate.
It is easy to rove that there exists at least onepal optim
solution which doesn’t include any inefficient candidate.
Therefore all the inefficient candidates are not considered
in the model without loss of the optimal solution. In
definition 1, min
i
E
S is the earliest possible start time and
max
i
LF is the latest allowable finish time of sub-project i.
ngest possible time window min max [, ]
ii
ES LF of
sub-project i is only a part of the whole project time
window [1, ]c, so to judge whether a candidate is ineffi-
cient or noe only need to do the judgment in time
window min max
[, ]
ii
ES LF according to definition 1, rather
The lo
n
t, w
than in the whole project time winw. This me-dothod im

Tabu Search Solution for Resource Confidence Considered Partner Selection Problem in Cross-Enterprise Project 551
proves th of definition 1 and the effect of
solution space reduction. Let min
i
q and max
i
qbe the short-
est and longest process time of sub-project i respectively,
min
1, 2,...,
min{ }
iiiim
i
qqqq,1,2,..., max }
iim
i
q qq,
then min
i
e satisfiability
max {
ii
q
E
Sand max
i
LF can be calculated with min
i
q and
max oject scheduling problem with the
,
i
q. This is a pr
objective of minimizing project mpan, i.e.akes
max
PS panre exists some polynomtime
ithms [13].
recC
r
Evalua
d the
m, th
ial
tur bng is selected
algo
3.2 Project-Scheduling-Based Solution
n Algorithm
In our TS algorith
tio
e naal numer stri
as code description. Let 12 [ ,,...,]
n
x
xx x, where i
x
is an
nds candidate integer between 1 and i m. This sta for that
i
x
is selected for sub-project i. Thus, 12 [ ,,...,]
n
x
xx x is
called a selection. For exa3 4] is a partner
selection of a project with 7 sub-projects. In the selection,
the candidate 3 is selected for the sub-project 1, and the
didate 4 is selected for the ub-proje
Once a selection fixes the candidates for all sub-pro-
jects, to obtain the object function value, a project-sche-
duling-based solution evaluation algorithm PSLP can be
done to calculate the variable values of cand
mp 1 5
cd so on.
le, [3 4
s
2
t 2, ancan
nij
E
, and
t (ii
also the object function value. The procedure of the algo-
rithm PSLP is described as follows:
Algorithm PSLP
Step 1: Calculate the earliest starting time i ES and the
earliest finish time i EF of each sub-projec

1, 2,...,)n. If do not exist ( ,,..., }k n)ki H{1, 2,


,
letion tim
e
{1,2,.. . ,k
, then
)i
jpe c
F.
i
LS and th
,..
}
n , then
}.
0
i
ES ; Else,max{,(}
ik
ESEF kH.
iiix
i
EFES q
.
: Calculate the pn. Let
,n LS E
late the latest starting tim
St
LF
lat
LF
ep 2
n
EF
Step 3: C
If do not
ro ect com
nn
cL
H,
n,
alc
n
S
u
exist (,i
e
est finish time i LF of each sub-project (1,2.,)ii n.
)k
;
in
LFElse, min{,( ,)
ik
LFLSikH i LS

iix
i
L
Fq.
Step 4: Calculate h sub-
1, 2,..s l
th
., )n
ot.
e flme eac
whe icritica
i
oat ti
judge
ii
i
FF of
ther itproject
sub-p
(ii
roject or
and
n
F
FLSES.
U, cal-
If 0
i
FF , then {}
cc
UUi , Else
{}
nc
UUi.
Step 5: For each sub-project in
nc
non-critical
culate the maximual expectation of
confidence by thstep-by-step right-shifted procedure.
nc
m mathematicresource
e
Step 5.1: If nc U

, then go to Step 6; Else he
non-critical sub-project i from nc
U which has the
maximum earliest start time. \{}
nc nc
UUi, 0Pos
get t

,
0
ixi
E

.
Step 5.2: For 0j

to If Do 1
i
FF 1
ixi
ixi
Eq 
1
()
jq
ixi
ix i
dES

i
kj
k

then
1
1()
jq
ixi
ixix i
ixi
EdE
q



ii
kj
Sk,
Pos j

End For.
Step 5.3: Adjust oat time of each immediate pre
ceding non-critical sub-project of sub-project i. Fo
the fl-
r
, and (,)ki
nc
kU H

, let kk
F
FFFPos, go to
St
he maximthematicectatiour
ep 5.1.
Step 6: For each critical sub-project c iU, calculate
tum maal expce con-
fidence,
n of reso
1
0
ix ix i
ii
k
ixi
1()
qixi
dESk

E

q

.
Step 7: Calculate the objective function value. ()
d
F
x
m
ni

 11
1
()(1[[]] )
c
n
ij ijn
jt i
xtEc D 

 


Step 8: Over.
In the PSLP algorithm, the time window of each sub-
project is calculated first. There,


, 1,...,
ii i
ES ESLS
d


, 1,
ii
EFEF..., i LF
roject set c U, the
an represent
do
, tha
rge-scale combination optimization problem.
rtcomings of
the starting time win-
al path, the critical
w and finish time windows of sub-project i, respec-
tively. In addition, the project critic
sub-p non-critical sub-project set nc U
and the float time of each sub-project can also be deter-
mined. In the second part, based on the idea of solving the
resource levelling project scheduling with fixed project
duration problemand considered the characteristics t
the resource confidence is various in each period and non-
critical sub-project has float time, a step-by-step right-
shifted procedure is employed to find the time section in
which the non-critical sub-project has the greatest mathe-
matical expectation of resource confidence. In the pro-
cedure, non-critical sub-projects are dealt with in accor-
dance with descending order of the earliest start time. At
the last part, the objective function value for a selection is
obtained.
4. Tabu Search Algorithm Design
The Tabu search (TS) algorithm is an effective method for
solving la
The TS algorithm can overcome the sho

Tabu Search Solution for Resource Confidence Considered Partner Selection Problem in Cross-Enterprise Project 552
one
e constringency speed to op-
the fact that, in the widest
some common heuristic algorithms which only adapt to
special problems and easily sink into local optimal solu-
tions. TS has been used on an increasing number of prac-
tice problem and has proven to be effective [14,15].
4.1 The Initial Solution
The initial solution is very important to TS and a good
is very useful to improve th
timal solution. Considering
feasible time window


, 1,...,ES ESLFof the sub-pro-
ject, the greater the resource confidence mathematical
expectation of the cand date is, the higher the probability
of being selected is, thgeneration pro-
cedure PINI is designed as the following steps.
Step 1: From sub-project 1i
i
e initial solution

to n, calculate the wid-
est feasible time window


,
ii
ES LF.
Step 2: From sub-project 1i

to n, find candidate i
x
which has the greatest m
source confidence in all thes
aatical expectation of
e cdatof sub-project
luti
them
andi
re-
i.
Step 3: output the initial soon 12
[ ,,...,]
n
x
xx x.
It is obvious that the initial solution is feasible.
4.2 Neighbourhood Structure and Candidate
is
s
obtgh changing the value of one bit of the
confidence and the step-
by
Solution
Considering the natural number string employed in th
algoghbor is defined as all feasible solutionrithm, nei
ained throu
current solution, i.e., changing a candidate partner of a
sub-project. Moving from the current solution to a solu-
tion in the neighborhood is called a move. Therefore, one
step in a move can change only one partner of the current
solution. Let NB be the neighbor set. Evaluation value of
each solution in NB can be calculated by the PSLP algo-
rithm. The solution in NB will be selected as the candidate
solution with meeting the conditions that it has the great-
est evaluation value and the move from the current solu-
tion to it is not in the Tabu list.
In the solution evaluation algorithm PSLP described in
3.2, Step 5 is to precisely calculate the maximum mathe-
matical expectation of resource
-step right-shifted procedure has high CPU time cost. In
fact, if a solution causes the whole project delayed, its
evaluation value will be penalized with the penalty factor

in the Formula 1. Therefore, the solution has very low
probability to be selected as the candidate solution. From
this point of view, the following tardiness penalty
aluation procedure of candidate solution CSTPE is
designed.
Procedure CSTPE:
Step 1: Implement the Steps 1-3 in the algorithm PSLP to
calculate t
ev
he time window of each sub-project and the
e whole project.
he time window
completion time of th
Step 2: If the project isn’t finished within the due date in
the solution, then the Step 5 of PSLP will not be run and
the subsequent steps will run with t


,
ii
ES LF obtained by the Steps 1-3, else the total PSLP
algorithm will be run.
Experiments show that this candidate solution evalua-
dure can significantly reduce the time cost and
still can find the optim
tion proce
al solution with high probability.
Th
sional
e number of rows is the length of the
t column is the code of the sub-project,
ling,
was found,
w
if a solution is
tions (max_tries) and the maximum number of itera-
tio
e detailed analysis is described in the Section 5.
4.3 Tabu List
The Tabu list (TSL) is composed of a two-dimen
integer array. Th
Tabu list, the firs
and the second column is the code of the candidate partner
corresponding to the sub-project in the first column. The
code for every row records a solution in the neighborhood
that has been deleted in recent movements. TSL is re-
newed according to the criterion of first in, first out.
4.4 Longer-Term Tabu List and Tabu Relaxation
To avoid getting into the local optimum and the cyc
two special techniques, longer-term Tabu list (TTL) and
Tabu relaxation, are used. TTL is created to dynamically
forbid moving overactive nodes in order to get diversifi-
cation and help to prevent cycling. The algorithm incor-
porates a move frequency table to record the move fre-
quency of each sub-project. When a sub-project’s partner
is changed, its move frequency is incremented by 1. If a
sub-project’s partner x has been moved more than two
times and TTL is not full, it will be put into TTL. If TTL is
full and if some sub-project’s candidate partner y already
in TTL has a lower move frequency than x, y will be
dropped and x will be added into TTL.
Another technique used is the relaxation of Tabu lists.
If a given number of iterations (relaxed_tries) has elapsed
and TTL is full since the last best solution
hich means the search process has plunged into a local
optimal solution or a cycling, both TSL and TTL are
emptied and using the current solution as the initial solu-
tion to continue the search. Relaxation of the Tabu lists
will change the neighborhood of the current solution
dramatically, which will lead to a rapid downhill move-
ment and may lead to new search spaces.
4.5 The Aspiration Criterion and Stopping Rule
The Tabu status of a move can be overruled
feasible and is better than any feasible solution known so
far.
In our PSTS algorithm, there are two ways of control-
ling the execution time: the maximum total number of
itera
ns without improvement of the best known feasible
solution (max_unchanged). The execution of the algo-

Tabu Search Solution for Resource Confidence Considered Partner Selection Problem in Cross-Enterprise Project 553
rithm is stopped when the number of iterations max_tries
and max_unchanged are both attained, or when the
number of iterations doubles max_tries. Therefore, the
total number of iterations is not known in advance, de-
pending on the evolution of the search. The combination
of the max_tries and the max_unchanged as stopping
criterion allows the search to continue if the algorithm is
exploring a new promising region. Obviously, to give
time for improvement after the restart, the max_un-
changed should be greater than the relaxed_tries.
4.6 Global Description of the Algorithm
Algorithm PSTS:
Step 1: Specify the parameters. Set initial
changed, relaxed_tries, set iteration
values of
, iteration counter for no improve-
max_tries, max_un
counter to tries 0
ment to 0unchanged.
Step 2: Generate an initial solution
x
using the algo-
rithm PINI ulate the evaluation value (x)F of and calc
x
using re.the CSE procedu Let the cunt best solution
*
rre
x
x, the best evaluation value *(x)FF.
Step 3: 1tries tries , if max_tries triesand
max_ ,ged unchangedor if 2 tries 
then go to Step 7
unchan
max_ tries , , else g
Step 4: If _tries, anll,
TSL and TTL.
Find the neighborhood NB of
o to Step 4.
relaxedunchangedd TTL is fu
then empty
Step 5:
x
, calculate the
caution ndidate solNB
x
and the evaluatio
solution
n value ()
NB
Fx .
Calculate the best Tabu TSL
x
and t
ng piration
he corre-
sponding evaluation value ()
TSL
Fx from TSL.
Step 6: Consideri the TSL,TLL and the as
criterion, generate the new solution
x
from NB
x
and
TSL
x
. If *max{ ()},FFxx* ), (
NB TSL
F,
x
x*
F
max{ (),()},
NB TSL
Fx Fx0;unchanged else
1unchanged unchanged . Go to Step 3.
7: OuStep tput *
x
and is the optimal solutio
algorithm is over.
If the CSTPE procedure is candidate
sobe
le
onsists of 14 sub-projects
*
Fn,
used to evaluate
lution, then the PSTS will named as PSTS-P. Other-
wise, if just the compted PSLP is used, the PSTS will be
named as PSTS-NP.
5. Experiments Analysis
The algorithm was coded by JAVA and run on a Pentium
Dual 2.2 GHz PC.
The example is a project that c
and the core enterprise calls tenderers for the sub-projects.
The precedence relationship represented by the active-
on-node network is shown in Figure 1. The numbers
Figure 1. Example of a project represented by active network
in the parentheses are the number of candidates, the shor
he project’s due date is 24 periods and each sub-project
t-
est process time and the longest process time, respectively.
T
has 3 to 6 candidates. The solution space size is 1.05 × 108.
Through identifying and removing the inefficient candi-
dates according to Definition 1, the size is reduced to 2.83
× 107. Different candidates may have different process
time to the sub-project that they bid for. The resource
confidence of the candidate in each period ()
ij
dt is cal-
culated by the fuzzy comprehensive evaluation method,
and where () (0,1]
ij
dt

. For the limitation of the paper
size, the detailed data is omitted.
The setting for the values of parameters is important for
the efficiencyrithm. In our algorithm, the “Best_
rate” is used to evaluate and adjust t
of TS algo
he values of parameters,
w
of the PSTS-P, PSTS-NP and
B
t it needs much more running time to deal with
la
here “Best_rate” is the rate to reach the optimal solution in
a certain number of runs. Based on the algorithms of IP WH
et al. [10] and Zhibin et al. [11], considering the character-
istics of our problem, a branch- bound algorithm (B & B) is
designed to calculate the optimal solution. For different
scale problems, the algorithm was run a certain number
times according to the scale of the problem with different
random seeds for each parameter setting. Therefore, the
parameters with the highest “Best_rate” are selected. To the
example in Figure 1, the values of the parameters are
“max_tries = 700”, “max_unchanged = 80”, “relaxed_tries
= 60”, the length of TSL is 18, and the length of TLL is 70.
The result of the example is shown in Table 1, and the
objective value is 0.241.
For testing the performance of the PSTS algorithm, we
randomly generated some problems with different scales.
The comparison results
&B are shown in Table 2. Where “N” is the number of
sub-projects, “size” stands for the size of solution space,
“CPU time” is the average computation time of each
running.
The B & B algorithm is a kind of exact algorithm and
can always find the optimal solution (best rate is always
100%), bu
rge scale problems. The two recommended algorithms,
PSTS-P and PSTS-NP, can achieve the optimal solution
with a high best rate and the computation time doesn’t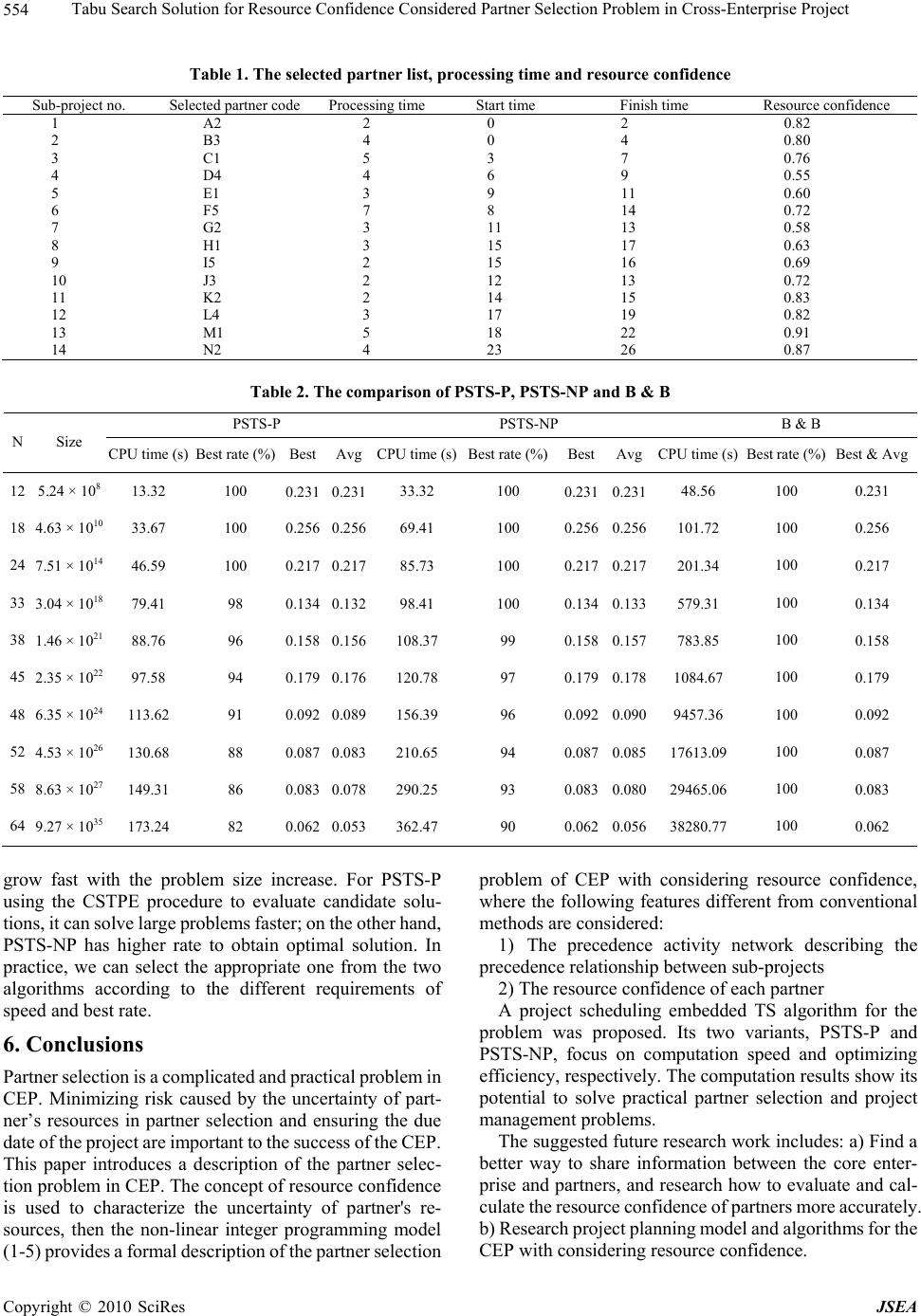

Tabu Search Solution for Resource Confidence Considered Partner Selection Problem in Cross-Enterprise Project 554
oce
Sub-project no. SeResource confidence
Table 1. The selected partner list, prssing time and resource confidence
lected partner code Processing timeStart time Finish time
1 A2 0.82 2 0 2
2 B3 4 0 4 0.80
3 C1 5 3 7 0.76
4 D4 4 6 9 0.55
5 E1 3 9 11
0.60
6 F5 7 8 140.72
7 G2 3 1113 0.58
8 H1 3 1517 0.63
9 I5 2 15 16 0.69
10 J3 2 12 13 0.72
11 K2 2 14 15 0.83
12 L4 3 17 19 0.82
13 M1 5 18 22 0.91
14 N2 4 23 26 0.87
Table 2. The coarison of PSTS-P, PSTS-NP and B & B
PSB & B
mp
TS-P PSTS-NP
N Size
CPU time (s) Best Best AvgCPU time (s)Best BestAvgCPU time (s) Best Best & Avgrate (%) rate (%)rate (%)
12 5.24 × 108 13.32 100 0.231 0.23133.32 100
0.231 0.23148.56 100 0.231
18 4.63 × 1010 33.67 100 0.256 0.25669.41 100 0.2560.256101.72 100 0.256
24 7.51 × 1014 46.59 100 0.217 0.21785.73 100 0.2170.217201.34 100 0.217
33 3.04 × 1018 79.41 98 0.134 0.13298.41 100 0.1340.133579.31 100 0.134
38 1.46 × 1021 88.76 96 0.158 0.156108.37 99 0.1580.157783.85 100 0.158
45 2.35 × 1022 97.58 94 0.179 0.176120.78 97 0.1790.1781084.67 100 0.179
48 6.35 × 1024 113.62 91 0.092 0.089156.39 96 0.0920.0909457.36 100 0.092
52 4.53 × 1026 130.68 88 0.087 0.083210.65 94 0.0870.08517613.09 100 0.087
58 8.63 × 1027 149.31 86 0.083 0.078290.25 93 0.0830.08029465.06 100 0.083
64 9.27 × 1035 173.24 82 0.062 0.053362.47 90 0.0620.05638280.77 100 0.062
row fast with the problem size increase. For PSTS-P
complicated and practical problem in
problem of CEP with considering resource confidence,
optimizing
ef
g
using the CSTPE procedure to evaluate candidate solu-
tions, it can solve large problems faster; on the other hand,
PSTS-NP has higher rate to obtain optimal solution. In
practice, we can select the appropriate one from the two
algorithms according to the different requirements of
speed and best rate.
6. Conclusions
Partner selection is a
CEP. Minimizing risk caused by the uncertainty of part-
ner’s resources in partner selection and ensuring the due
date of the project are important to the success of the CEP.
This paper introduces a description of the partner selec-
tion problem in CEP. The concept of resource confidence
is used to characterize the uncertainty of partner's re-
sources, then the non-linear integer programming model
(1-5) provides a formal description of the partner selection
where the following features different from conventional
methods are considered:
1) The precedence activity network describing the
precedence relationship between sub-projects
2) The resource confidence of each partner
A project scheduling embedded TS algorithm for the
problem was proposed. Its two variants, PSTS-P and
PSTS-NP, focus on computation speed and
ficiency, respectively. The computation results show its
potential to solve practical partner selection and project
management problems.
The suggested future research work includes: a) Find a
better way to share information between the core enter-
prise and partners, and research how to evaluate and cal-
culate the resource confidence of partners more accurately.
b) Research project planning model and algorithms for the
CEP with considering resource confidence.

Tabu Search Solution for Resource Confidence Considered Partner Selection Problem in Cross-Enterprise Project 555
REFERENCES
[1] X. F. Xu, “Virtual Organization - the Enterprise Organi-
zation Form in the Future,” in Chinese, China Me-
chanical Eengineering, Vol. 7, No. 4, 1996, pp. 15-20.
[2] H. S. Jagdev anded Enterprise - A
Context for ction Planning &
n
“A Review of
jidimitriou and A. C. Georgiou, “A Goal
ion in a Global Manu-
ter-Integrated
anu-
plied
n for a Risk-Based Partner Selection Problem
ification, Mo-
206.
nd J. Browne, “The Exte
Manufacturing,” Produ
fac
Control, Vol. 9, No. 3, 1998, pp. 216-229.
[3] M. J. Maloni and W. C. Benton, “Supply Chain Partner-
ships: Opportunities for Operations Research,” Europea
Man
Journal of Operational Research, Vol. 101, No. 3, 1997,
pp. 419-429.
[4] L. D. Boer, E. Labro and P. Morlacchi,
Fact
Methods Supporting Supplier Selection,” European
Journal of Purchasing & Supply Management, Vol. 7, No.
2, 2001, pp. 75-89.
[5] A. Yannis, Ha
Programming Model for Partner Selection Decisions in
International Joint Ventures,” European Journal of
Operational Research, Vol. 138, No. 3, 2002, pp. 649-
662.
[6] D. Y. Sha and Z. H. Che, “Virtual Integration with a
Multi-Criteria Partner Selection Model for the Multi-
Echelon Manufacturing System,” International Journal of
Advanced Manufacturing Technology, Vol. 25, No. 7-8,
2005, pp. 793-802.
[7] L. Mikhailov, “Fuzzy Analytical Approach to Partnership
Selection in Formation of Virtual Enterprises,” Omega,
Vol. 30, No. 5, 2002, pp. 393-401.
[8] D. Wang, K. L. Yung and W. H. Ip, “A Heuristic Genetic
Algorithm for Subcontractor Select
turing Environment,” IEEE Transactions on SMC
Part-C, Vol. 31, No. 2, 2001, pp. 189-198.
[9] N. Q. Wu and P. Su, “Selection of Partners in Virtual
Enterprise Paradigm,” Robotics and Compu
ufacturing, Vol. 21, No. 2, 2005, pp. 119-131.
[10] W. H. Ip, D. Wang and K. L. Yung, “A Branch and Bound
Algorithm for Sub-Contractor Selection in Agile M
uring Environment,” International Journal of Produc-
tion Economics, Vol. 87, No. 2, 2004, pp. 195-205.
[11] Z. B. Zeng, Y. Li and W. X. Zhu, “Partner Selection with a
Due Date Constraint in Virtual Enterprises,” Ap
Mathematics and Computation, Vol. 175, No. 2, 2006, pp.
1353-1365.
[12] W. H. Ip, M. Huang, K. L. Yung, et al. ”Genetic Algo-
rithm Solutio
in a Virtual Enterprise,” Computers & Operations Re-
search, Vol. 30, No. 2, 2003, pp. 213-231.
[13] P. Brucker, A. Drexl and R. Möhring, “Resource-Cons-
trained Project Scheduling: Notation, Class
dels, and Methods,” European Journal of Operational Re-
search, Vol. 112, No. 1, 1999, pp. 3-41.
[14] F. Glover, “Tabu Search: Part I,” ORSA Journal on
Computing, Vol. 1, No. 3, 1989, pp. 190-
[15] F. Glover, “Tabu Search: Part II,” ORSA Journal on
Computing, Vol. 2, No. 1, 1990, pp. 4-32.