Wireless Sensor Network, 2010, 2, 411-418
doi:10.4236/wsn.2010.26053 Published Online June 2010 (http://www.SciRP.org/journal/wsn)
Heuristic Spectrum Assignment Algorithm
in Distributed Cognitive Networks
Li Yu, Cong Liu, Zuhao Liu, Wenyu Hu
Huazhong University of Science and Technology, Department of Electronic Information Engineering,
Wuhan National Laboratory for Optoelectronics, Div Commun and Intelligent Networks, Wuhan, China
Received December 14, 2009; revised February 5, 2010; accepted February 10, 2010
Abstract
Cognitive radio is an exciting emerging technology that has the potential of dealing with the urgent require-
ment and scarcity of the radio spectrum. Although having multiple radio interfaces and available spectrum
bands can generally increase the effective throughput, a problem arises as to what the best strategy to dy-
namically assign available bands to secondary users for maximizing throughput by minimizing the interfer-
ence, and what the best scheme to allocate the spectrum holes to unlicensed users to maximize the fairness.
This paper presents a distributed and heuristic spectrum assignment algorithm for multi-radio wireless cogni-
tive networks in a cognitive network environment. The proposed algorithm (Fairness Bargaining with Max-
imum throughput, FBMT) considers the problems including system throughput and the fairness. Extensive
simulation studies in 802.11 based multi-radio cognitive networks have been performed. The results indicate
that the proposed algorithm can facilitate a large increase in network throughput and acquire a good fairness
performance in comparison with a common spectrum assignment mechanism that is used as a benchmark in
the literature.
Keywords: Cognitive Network, Distributed Spectrum Assignment, Throughput, Fairness, FBMT
1. Introduction
As wireless technologies continue to grow, more and
more spectrum resources will be needed. Within the cur-
rent spectrum regulatory framework, however, all of the
frequency bands are exclusively allocated to specific
services, and no violation from unlicensed users is al-
lowed. A recent survey of spectrum utilization made by
the Federal Communications Commission (FCC) has
indicated that the actual licensed spectrum is largely un-
derutilized in vast temporal and geographic dimensions
[1]. For instance, a field spectrum measurement taken in
New York City has shown that the maximum total spec-
trum occupancy is only 13.1% from 30 MHz to 3 GHz
[2,3]. Similar results, obtained in the most crowded area
of downtown Washington, D.C., indicated occupancy of
less than 35% of the radio spectrum below 3 GHz. More-
over, the spectrum usage varies significantly in various
time, frequency, and geographic locations.
1.1. Spectrum Opportunity
Spectrum segments in a licensed band that are currently
unused by its primary users (PU) are referred to as the
spectrum opportunity/holes. Spectrum holes appear as
useable spectrum bands to a secondary user (SU) with
respect to the licensed band in question. For a secondary
user, given its locations, a set of spectrum holes can be
available at a given time. Such a set of available bands
are referred to as the spectrum opportunity of the secon-
dary user.
Spectrum utilization can be improved significantly by
allowing a secondary user to utilize this spectrum oppor-
tunity when the primary user is absent. Cognitive radio
(CR), as an agile radio technology, has been proposed to
promote the efficient use of the spectrum [4]. By sensing
and adapting to the environment, a CR is able to fill in
spectrum holes and serve its users without causing harmful
interference to the licensed user.
Amid these usage trends, it is desirable to introduce
dynamic spectrum allocation strategies so that the unused
segments of a licensed band which owned by its primary
users can be used by unlicensed or secondary users. A
fixed spectrum policy was sufficient in the past but with
the increasing disparity in utilization rate between the
licensed and unlicensed bands, dynamic spectrum alloca-

412 L. YU ET AL.
tion policies are needed.
1.2. Related Work
Dynamic spectrum allocation strategies enable secondary
user to sense local usable bands (including the bands
without license), and to use them by some certain rules/
algorithms without interference to primary users. Ac-
cording to the difference of structures of networks, the
algorithms can be divided into two categories: the cen-
tralized and the distributed. In centralized spectrum allo-
cation algorithms, due to higher computing complexity,
the centralized control devices become a bottle-neck be-
cause they are not competent for such complex comput-
ing work. So the distributed algorithms are much better
than the centralized algorithm in spectrum assignment.
Most distributed algorithms adopt heuristic assignment
methods, in which algorithm’s astringency is a very im-
portant target, and the higher the astringency of algo-
rithms is, the better the algorithm can adapt to the time-
varying systems. Beside astringency, in [5-7], Zheng
et al. put forward other two basic targets, Max-Sum-
Bandwidth (MSB) and Max-Min-Bandwidth (MMB),
these targets are used to describe the improvement of
throughput that the algorithm brings to system. In [8],
Cao et al. proposed a FBFP (fairness bargaining with
feed poverty) algorithm to Ad Hoc networks, in this
algorithm, secondary users are divided into different
groups based on their regions. Simulation result present
that this algorithm can decrease the computing complex-
ity effectively but increase the system cost because it
needs extra packet to set up and maintain the groups. In
[9,10], Wang and Liu proposed several algorithms which
based on the max-spectrum-employ rate and max- fair-
ness, but the throughput of system is absent in their con-
sideration. In [11], by using the time-continuous Markov
chain to model the spectrum access, Xing et al. proposed
a random spectrum access algorithm, but this algorithm
is only applicable in simple systems which consist of
fewer primary users and secondary users.
Motivated by this, considering both the fairness and
throughput, we bring forward a heuristic algorithm called
Fairness Bargaining with Maximum Throughput (FBMT).
The simulation will demonstrate that FBMT not only
contribute to promote the systems fairness, but also im-
prove the system throughput.
The rest of this paper is organized as follows. In Sec-
tion 2, a completely distributed system model will be
briefly reviewed, and a mathematic model will be de-
signed for the spectrum assignment and coordination
process. In Section 3, we give the detailed description
of FBMT. We evaluate the performance of FBMT by
our simulation in Section 4. Finally, we conclude the
paper.
2. Preliminary
2.1. Wireless Cognitive Network Architecture
First, we characterize a distributed system model:
M
primary users and secondary users are randomly
distributed in an
N
X
Y

area (Figure 1(a)), secondary
can using a certain signal detection techniques such as
matched filter detection, energy detection or cyclosta-
tionary detection to get the usable spectrum opportunity.
In the system, available spectrums are divided into
K
completely orthogonal bands. We assume that these
bands are symmetric, which means that these bands have
the same bandwidth, meanwhile, have the same spectrum
quality and the spectrum availability. We also assume
that the interference between two nodes only rest with
the relative distance of theirs, all of the primary users and
Figure 1. (a) Sketch map of the cognitive radio system; (b) An example of cognitive radio system.

L. YU ET AL. 413
secondary users utilize the omni-antenna, we define the
transmission radius of primary users and secondary
users are (, )
rp ik

and (, )
rs jk

respectively, where
and denote the serial number of the primary
user, secondary user and spectrum bands respectively.
If the distance between the primary user and secondary
user is greater than
,ij k
(, )rs ik ( ,)
rp jk


 , the secondary
user will not conflict with primary user when they se-
lect the same band to propagate data simultaneously. In
order to analyze simply, we assume that all of the pri-
mary users have the same transmission range (express
as rp

), and all of the secondary users have the same
transmission range (express as rs

). Moreover, we
define that the node and are neighbours if their
transmission coverage area is overlapped with each
other.
ij
Figure 1(b) depicts generic wireless cognitive net-
work architecture. The network consists of four primary
users and five secondary users; there are three orthogonal
wireless bands which are denoted by Ⅰ, Ⅱ and Ⅲ.
From the figure we can see that the transmission range of
SU3 conflicts with the transmission of PU3 and PU4,
which occupy the band Ⅰand Ⅲ respectively. Definitely,
SU3 can only utilize the spectrum Ⅱto transmit data. As
for SU1, it can use the spectrum , and without ⅠⅡ Ⅲ
interference to any PUs; As for SU2, it also can use the
spectrum Ⅰ, and , meanwhile, SUⅡⅢ 2 and SU1 is
neighbour node mutually, in order to avoid the conflict
between them, they cannot use the same spectrum to
propagate data simultaneously. We need to establish
some rules to assign the available spectrums to each
secondary user. In this paper, we aim to maximize the
system throughput by maximize the total spectrum utili-
zation rate.
2.2. Definitions
1) In a network waiting for spectrum assignment, there
are secondary users indexed from 1 to compet-
ing for
N N
K
spectrum bands indexed 1 to
K
.
2)

,1,..., ;1,..., ik
Ssi NkK characterize the
per user available spectrum, i.e., spectrum band is
available for user if
k
i,1
ik
s

. Due to differences in
user locations, technology employed in different spec-
trums and user requirements, different users will per-
ceive different available spectrum. In Figure 1(b), we
can obtain
110 01
11111
1101 1
T
S





3) We also consider that the throughput achieved by
different bands is different, depending on the user’s en-
vironment and the attribute of spectrums. Let


,1,..., ;1,..., ik
Bbi Nk K
describe the reward that a user gets by successfully
acquiring available spectrum band , i.e., repres-
ents the maximum throughput that can be acquired (as-
suming no interference from other neighbours). Let
i
k,ik b


,,


Bikik
N
K
Ssb
denote the bandwidth weighted available spectrum.
4) We characterize interference between two compet-
ing users by a constraint set. Let



,, ,,0,1 

ijk ijk
N
MK
Cc c
represent the constraint, where if , users and
can cause interference if they use the spectrum band
simultaneously.
,, 1 ijk
ci
j
k
5) We define a valid spectrum assignment



,, 0,1 ik ik
N
K
Aaa  
where ,1
ik
a

denotes that spectrum band is as-
signed to user ,
k
i
A
satisfies all the constraints defined
by , that is: C
,, ,,
0, 1;,;
ikjki jk
aa ifcijNkK

 (1)
Finally, we use ,
N
K

to denote the set of valid spec-
trum assignments for a given set of users and N
K
spectrum bands.
6) We must pay attention that different secondary us-
ers have different neighbors in different bands, which
means that different secondary users have various influ-
ence to system throughput if they are assigned to identi-
cal band. We must take this heterogeneity into consid-
eration in spectrum allocation process, we define the gain
matrix


,1,..., ;1,..., ik
RriNkK
to describe this impact, where ,, /
ikik ik
rb,

, ,ik

is
the neighbor numbers of user in spectrum band . i k
2.3. Optimization Problems
The objective of a general resource allocation problem
can be defined in terms of a utility function. In spectrum
related resource allocation problems, we usually need to
solve the optimization problem expressed as follows:
1) Max-Sum-Bandwidth (MSB): This aims to maxi-
C
opyright © 2010 SciRes. WSN

414 L. YU ET AL.
mize the total spectrum utilization in the system. The
optimization problem is expressed as:
,
,,
11
max
NK
NK
ik ik
Aik
s
b
 

 (2)
2) Max-Min-Bandwidth (MMB): This aims to maxi-
mize the bottleneck user’s spectrum utilization. The op-
timization problem can be expressed by:
,
,,
1
max min
NK
K
ik ik
iN Ak
s
b
  

 (3)
2.4. Color-Sensitive Graph Coloring Problem
By mapping each spectrum into a color, the spectrum
allocation problem can be simplified as a GMC (Graph
Multi-Coloring) problem. First, we define a bidirectional
graph , where is a set of nodes de-
noting the users that share the spectrums,

,,
CB
GVES

V
B
S
kc
c
k
represents
the bandwidth weighted available spectrum as defined in
Section 2.2, or the color list at each node, and is a
set of undirected edges between nodes representing in-
terference constraints between two nodes defined by .
For any two distinct nodes , an edge
between and , is in if and only if 1.
Hence, any two distinct nodes can have multiple colored
edges between them. We define the color specific
degree of a node , i.e.,
C
E
olor
,, = ijk
C
,ij
C
,ik
V
i j
i
E

to represent the number of
neighbours that are color mutually constrained with
(those who can not use if i uses color ). It is also
a relatively good measure of the impact (to neighbours)
when assigning a color to a node. The equivalent graph
coloring problem is to color each node using a number of
colors from its color list, such that if a color edge ex-
ists between any two distinct nodes, they can’t be colored
with simultaneously. We name this the Color Sensi-
tive Graph Coloring (CSGC) problem.
k i
k k
k
k
3. Proposed Spectrum Assignment
Algorithm
The optimal coloring problem is known to be NP-hard. In
this section, we discuss a set of heuristic based approaches
that produce good coloring solutions. In particularly, we
extend some of the well-known graph coloring solutions
toward our problem settings and optimization goals.
3.1. The Analysis of Existing Algorithms
3.1.1. Collaborative-Max-Sum-Bandwidth Rule
This rule aims to maximize the sum of bandwidth weig-
hted color usage, corresponding to MSB optimization
defined in (2). When a node is assigned with a color
, his contribution to the sum bandwidth in a local
neighborhood can be computed as
i
k
,,
/
ik ik
b

since his
neighbors can not use the color. Here ,ik

represents the
number of color constrained neighbour of a node
in the current graph. We propose to label the node ac-
cording to
k i
,
max /
i
iik
ks
label b
,ik


(4)
,
arg max/
i
iik
ks
color b
,ik


(5)
where represents the color list available at node i at
this stage. This rule considers the tradeoff between spec-
trum utilization (in terms of selecting the color with the
largest bandwidth) and interference to neighbours. This
rule enables collaboration by taking into account the im-
pact to neighbours. If two nodes have the same label,
then the node with lower assigned bandwidth weighted
colors will get a higher label.
i
s
3.1.2. Random (RAND) Rule
Each node generates a random label which is between
, where denote the threshold of
the node i. At the beginning of the allocation, all of the
nodes have the same threshold. In an allocation process,
if node i get a color, , else
[0, ]
i
window
i
window wi
i
window
win
2
i
/2
i
dow windowi
ndow

. In each stage, each node labels
itself according to the above labeling rules, and broad-
casts the label to his neighbors. A node with the maxi-
mum label within his neighborhood gets to grab the color
associated with his label and broadcasts the color as-
signment to his neighbors. After collecting assignment
information from surrounding neighbors, each node up-
dates his color list and recalculates the label. This proc-
ess is repeated until the color list at each node is ex-
hausted or all the nodes are satisfied.
Although RAND can optimize fairness performance in
spectrum allocation process, however, it cannot guaran-
tee the network throughput. This will be demonstrated in
next section.
3.2. Fairness Bargaining with Maximum
Throughput (FBMT)
In this section, we describe the Fairness Bargaining with
Maximum Throughput algorithm-a distributed heuristic
spectrum assignment strategy.
The algorithm is based on the following assumptions:
1) Distributed wireless network architectures.
2) All the primary users have the same transmission
range, the same to secondary users.
3) All of the secondary users can detect and utilize all

L. YU ET AL. 415
,
of the spectrum holes.
4) Primary users have the preferential right of spec-
trum bands.
5) Users can communicate with each other by using
some mechanism.
In FBMT algorithm, we aim to maximize the sum of
bandwidth, corresponding to MSB optimization defined
in (2). When a node is assigned with a color , its
contribution to the sum bandwidth in a local neighbour-
hood can be computed as
i k
,,
/
ikik ik
rb


. We also search
for the fairness in spectrum distribution, defined a fair-
ness factor, which can be expressed by

,
1
,
,
1
12
() .
(1)
N
ij rs
j
ik K
ik
k
d
ft
st








(6)
where denotes current allocation times, numerator
denotes the neighbour numbers of node in spectrum
band , denominator means the number of bands which
is assigned to node before the assignment, d
denotes the distance between the node and node .
We define
t
k
i
i-tth ,ij
j
i

,,
1
() 12
N
iki jrs
j
ft d





(7)
if .
,
1
(1)0
K
ik
k
st



In FBMT, We propose to label the node according to
,,
max( )
i
iikik
ks
labelrf t

 (8)
,,
arg max()
i
iik
ks
colorrft


ik
K

(9)
where . This rule not only consid-
ers the tradeoff between spectrum utilization and inter-
ference to neighbours, but also considers the fairness in
spectrum allocation by introduction of the fairness factor.
1,..., ,1,...,iNk
The Pseudo code of HBTM algorithm is shown in Fig-
ure 2.
4. Performance
4.1. Performance Index
We often evaluate an algorithm by the throughput and
fairness it can achieve in spectrum allocation. The throu-
ghput, as defined herein, is the sum of bands each user is
assigned, which can be expressed by
,, ,
11
() ,
NK
Throughputi ki kNK
ik
AabA


 (10)
A

0
,
()
ik
f
t
1i

N
1k

K
,
()1
ik
st


,,
,,1
(, )(()()), max
1,,
ik ik
ijk
RwdWgh ikr tft
jNjic



,
()(, )
ik
rt Rwdik
,
()(, )
ik
rt Rwdik
i
,
1
ik
a

,,SR
,
(1)
ik
ft
Equation (6)
Figure 2. Pseudo code of HBTM algorithm.
In order to analysis the fairness of each spectrum algo-
rithms, we also define the fairness
2
,,
11
2
,,
11
(),
NK
ik ik
ik
f
airnessN K
NK
ik ik
ik
ab
AA
Nab







 










(11)
In (11), we can conclude that , the
more closely the
[0,1]
fairness
f
airness

approach to 1, the more im-
partial the process of spectrum allocation has. We also
define
2
,,
11
(),
NK
f
airnessi kikNK
ik
AabA



 


 (12)
if
2
,
11
,0
NK
ik
ik
ik
ab






 .
4.2. Simulations
4.2.1. Simulation Parameters
In this section we evaluate the performance of FBMT,
We design and implement a prototype system which
consists of some primary users and some secondary users,
these users are deployed at random in our simulation.
Our experiments apply following evaluation metrics:
 The throughput Throughput

;
 The fairness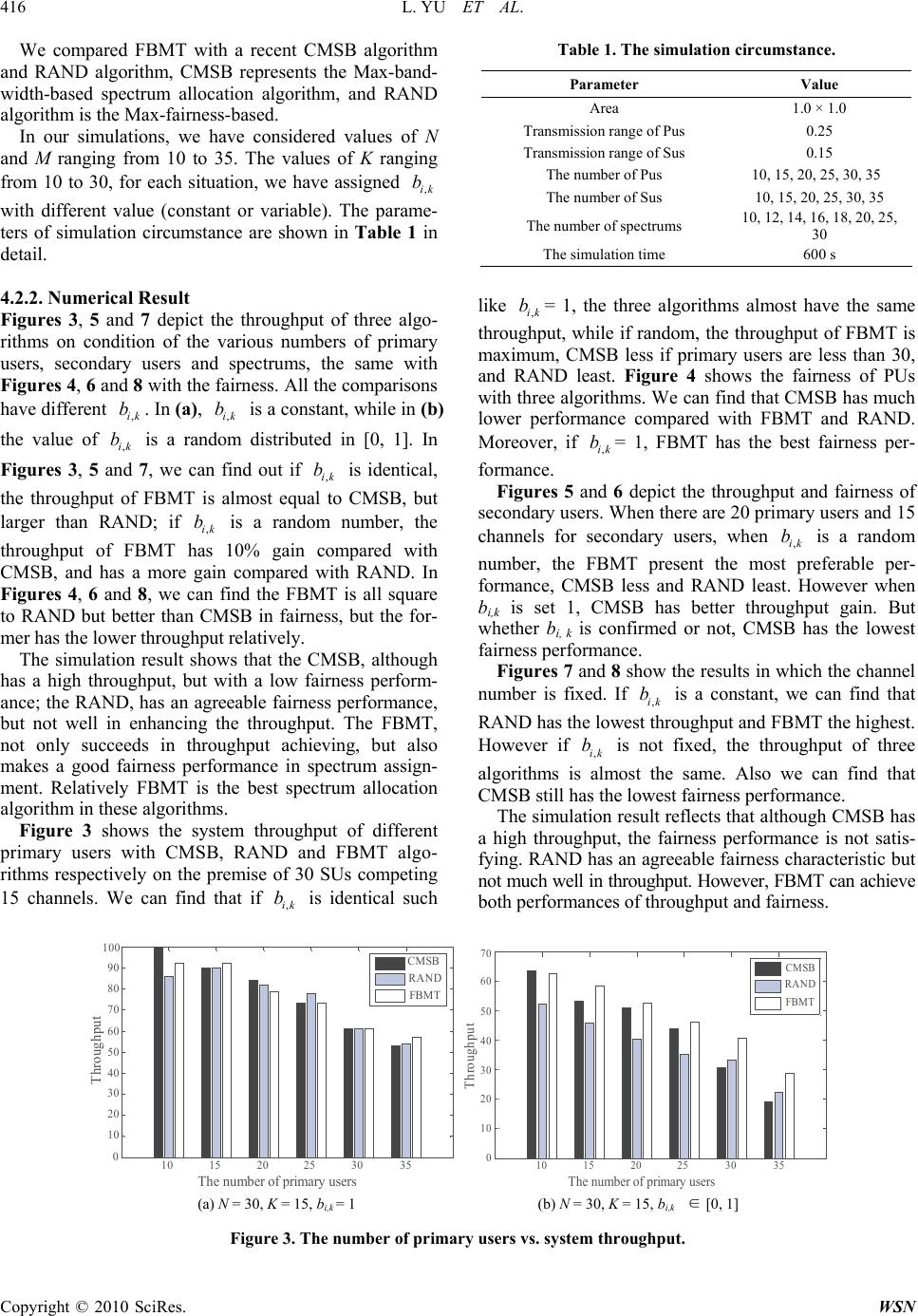
f
airness

;

416 L. YU ET AL.
We compared FBMT with a recent CMSB algorithm
and RAND algorithm, CMSB represents the Max-band-
width-based spectrum allocation algorithm, and RAND
algorithm is the Max-fairness-based.
Table 1. The simulation circumstance.
Parameter Value
Area 1.0 × 1.0
Transmission range of Pus 0.25
Transmission range of Sus 0.15
The number of Pus 10, 15, 20, 25, 30, 35
The number of Sus 10, 15, 20, 25, 30, 35
The number of spectrums 10, 12, 14, 16, 18, 20, 25,
30
The simulation time 600 s
In our simulations, we have considered values of N
and M ranging from 10 to 35. The values of K ranging
from 10 to 30, for each situation, we have assigned
with different value (constant or variable). The parame-
ters of simulation circumstance are shown in Table 1 in
detail.
,ik
b
4.2.2. Numerical Result like = 1, the three algorithms almost have the same
throughput, while if random, the throughput of FBMT is
maximum, CMSB less if primary users are less than 30,
and RAND least. Figure 4 shows the fairness of PUs
with three algorithms. We can find that CMSB has much
lower performance compared with FBMT and RAND.
Moreover, if = 1, FBMT has the best fairness per-
formance.
,ik
b
,ik
b
Figures 3, 5 and 7 depict the throughput of three algo-
rithms on condition of the various numbers of primary
users, secondary users and spectrums, the same with
Figures 4, 6 and 8 with the fairness. All the comparisons
have different . In (a), is a constant, while in (b)
the value of is a random distributed in [0, 1]. In
Figures 3, 5 and 7, we can find out if is identical,
the throughput of FBMT is almost equal to CMSB, but
larger than RAND; if b is a random number, the
throughput of FBMT has 10% gain compared with
CMSB, and has a more gain compared with RAND. In
Figures 4, 6 and 8, we can find the FBMT is all square
to RAND but better than CMSB in fairness, but the for-
mer has the lower throughput relatively.
,ik
b
,ik
b
,ik
b
,ik
,ik
b
Figures 5 and 6 depict the throughput and fairness of
secondary users. When there are 20 primary users and 15
channels for secondary users, when is a random
number, the FBMT present the most preferable per-
formance, CMSB less and RAND least. However when
bi,k is set 1, CMSB has better throughput gain. But
whether bi, k is confirmed or not, CMSB has the lowest
fairness performance.
,ik
b
The simulation result shows that the CMSB, although
has a high throughput, but with a low fairness perform-
ance; the RAND, has an agreeable fairness performance,
but not well in enhancing the throughput. The FBMT,
not only succeeds in throughput achieving, but also
makes a good fairness performance in spectrum assign-
ment. Relatively FBMT is the best spectrum allocation
algorithm in these algorithms.
Figures 7 and 8 show the results in which the channel
number is fixed. If is a constant, we can find that
RAND has the lowest throughput and FBMT the highest.
However if is not fixed, the throughput of three
algorithms is almost the same. Also we can find that
CMSB still has the lowest fairness performance.
,ik
b
,ik
b
The simulation result reflects that although CMSB has
a high throughput, the fairness performance is not satis-
fying. RAND has an agreeable fairness characteristic but
not much well in throughput. However, FBMT can achieve
both performances of throughput and fairness.
Figure 3 shows the system throughput of different
primary users with CMSB, RAND and FBMT algo-
rithms respectively on the premise of 30 SUs competing
15 channels. We can find that if is identical such
,ik
b
Throughput
The number of
p
rimar
y
users
CMSB
RAN D
FBMT
0
70
60
50
40
30
20
10
3025201510 35
90
100
80
Throughput
The number of
p
rimar
y
users
CMSB
RAN D
FBMT
0
70
60
50
40
30
20
10
3025201510 35
(a) N = 30, K = 15, bi,k = 1 (b) N = 30, K = 15, bi,k ∈ [0, 1]
Figure 3. The number of primary users vs. system throughput.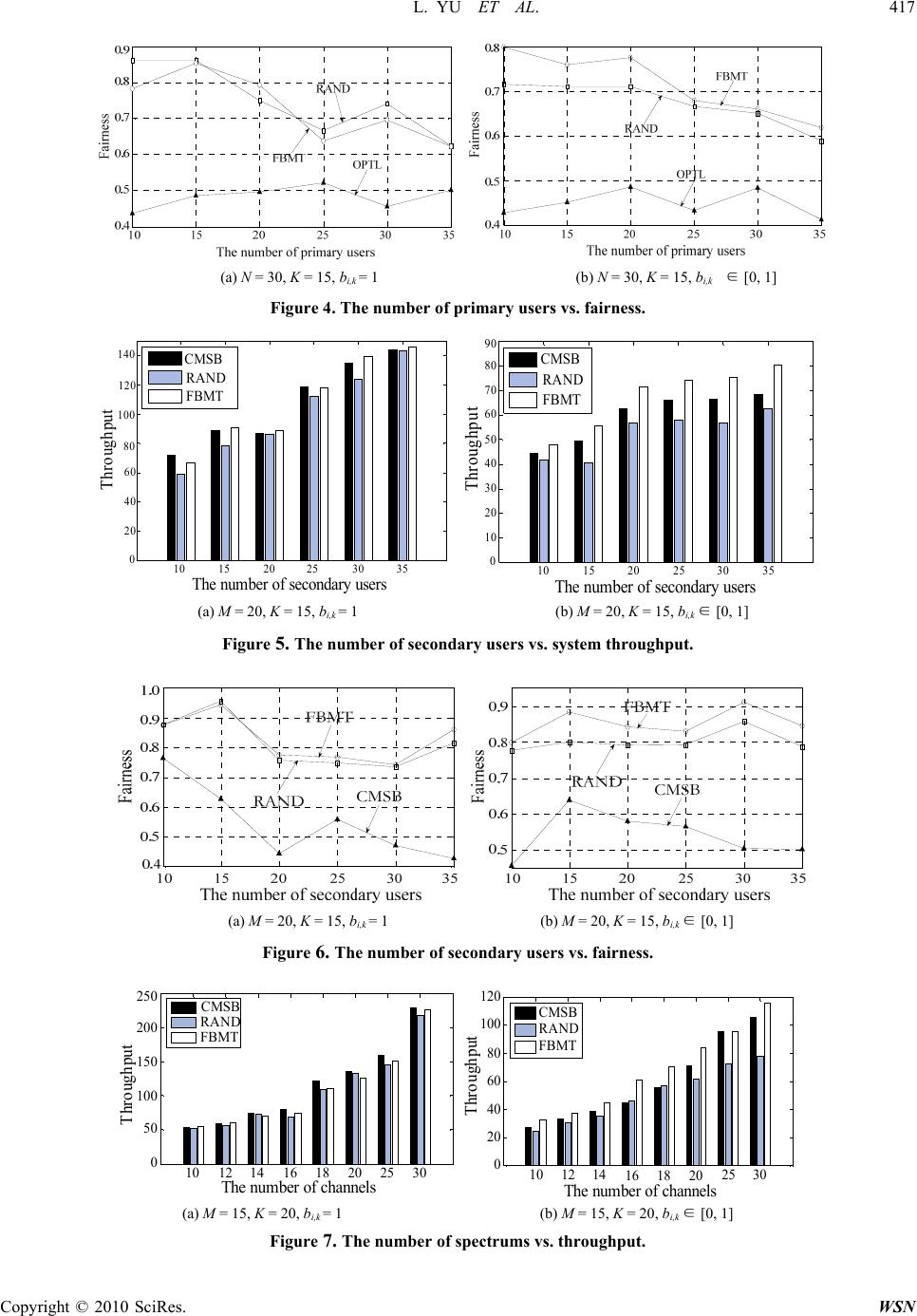

L. YU ET AL. 417
(a) N = 30, K = 15, bi,k = 1 (b) N = 30, K = 15, bi,k ∈ [0, 1]
Figure 4. The number of primary users vs. fairness.
Throughput
The number of secondary users
CMSB
RAND
FBMT
0
120
100
80
60
40
20
3025201510 35
140
Throughpu t
The number of secondar
y
users
CMSB
RAND
FBMT
0
70
60
50
40
30
20
10
3025201510 35
90
80
(a) M = 20, K = 15, bi,k = 1 (b) M = 20, K = 15, bi,k ∈ [0, 1]
Figure 5. The number of secondary users vs. system throughput.
(a) M = 20, K = 15, bi,k = 1 (b) M = 20, K = 15, bi,k ∈ [0, 1]
Figure 6. The number of secondary users vs. fairness.
10
250
200
150
100
50
030252018161412
CMSB
FBMT
RAND
The number of channels
Throughput
10
100
80
60
40
20
03025
201816 1412
CMSB
FBMT
RAND
The number of channels
Throughput
120
(a) M = 15, K = 20, bi,k = 1 (b) M = 15, K = 20, bi,k ∈ [0, 1]
Figure 7. The number of spectrums vs. throughput.

418 L. YU ET AL.
(a) M = 15, K = 20, bi,k = 1 (b) M = 15, K = 20, bi,k ∈ [0, 1]
Figure 8. The number of spectrums vs. fairness.
5. Conclusions [4] J. Mitola and G. Q. Maguire, “Cognitive Radio: Making
Software Radios More Personal,” IEEE Personal Com-
munications, Vol. 8, No. 6, 1999, pp. 13-18.
In this paper, we explore the tradeoff in spectrum utiliza-
tion and interference mitigation in open spectrum system.
We develop a new graph-theoretical model to character-
ize the spectrum access problem under a number of dif-
ferent optimization functions, taking into account het-
erogeneity in both spectrum availability, reward and in-
terference constraint.
[5] H. Zheng and C. Peng, “Collaboration and Fairness in
Opportunistic Spectrum Access,” Proceedings of the
2005 IEEE International Conference on Communications
(ICC’05), Seoul, Korea, 2005, pp. 3132-3136.
[6] C. Peng, H. Zheng and B. Y. Zhao, “Utilization and
Fairness in Spectrum Assignment for Opportunistic Spec-
trum Access,” Mobile Networks and Applications, Vol.
11, No. 4, 2006, pp. 555-576.
We then propose an algorithm where each user can
opportunistically utilize its available spectrum. Experi-
mental results confirm that our algorithm significant
benefits most in system throughput and also have a good
performance in fairness.
[7] J. Zhao, H. Zheng and G. Yang, “Distributed Coordina-
tion in Dynamic Spectrum Allocation Networks,” Pro-
ceedings of the 2005 1st IEEE International Symposium
on New Frontiers in Dynamic Spectrum Access Networks
(DySPAN’05), Baltimore, 2005, pp. 259-268.
6. Acknowledgements [8] L. Cao and H. Zheng, “Distributed Spectrum Allocation
Via Local Bargaining,” Proceedings of the 2nd Annual
IEEE Communications Society Conference on Sensor and
Ad Hoc Communications and Networks, Santa Clara,
2005, pp. 475-486.
This work was supported in part by National 863 Pro-
jects of China (2009AA01Z205), Fund of National Labo-
ratory (P080010) and Program for New Century Excel-
lent Talents in University (NCET070339). [9] X. Liu and W. Wang, “On the Characteristics of Spec-
trum-Agile Communication Networks,” Proceedings of
the 2005 1st IEEE International Symposium on New
Frontiers in Dynamic Spectrum Access Networks (DySP-
AN’05), Baltimore, 2005, pp. 214-223.
7. References
[1] S. W. Ellingson, “Spectrum Occupancy at VHF: Implica-
tions for Frequency-Agile Cognitive Radios,” Proceed-
ings of IEEE Vehicle Technologies Conference, Vol. 9,
No. 2, 2005, pp. 1379-1382.
[10] W. Wang and X. Liu, “List-Coloring Based Spectrum
Allocation for Open-Spectrum Wireless Networks,” Pro-
ceedings of the IEEE International Symposium on Ve-
hicular Technology (VTC’05-Fall), Dallas, 2005, pp.
690-694.
[2] M. A. McHenry, “NSF Spectrum Occupancy Measure-
ments Project Summary,” Shared Spectrum Company
Report, Vienna, 2005. [11] Y. Xing, R. Chandramouli, S. Mangold and S. N. Shan-
kar, “Analysis and Performance Evaluation of a Fair
Spectrum Access Protocol for Open Spectrum Wireless
Networks,” Proceedings of the 2005 IEEE International
Symposium on Communications (ICC’05), Seoul, Korea,
2005, pp. 1179-1183.
[3] M. McHenry, E. Livsics, T. Nguyen and N. Majumdar,
“XG Dynamic Spectrum Access Field Test Results,”
IEEE Communications Magazine, Vol. 6, No. 45, 2007,
pp. 51-57.