Smart Grid and Renewable Energy, 2010, 1, 54-61
doi:10.4236/sgre.2010.11009 Published Online May 2010 (http://www.SciRP.org/journal/sgre)
A MPCC-NLP Approach for an Electric Power
Market Problem
Helena Sofia Rodrigues1, Maria Teresa Torres Monteiro2, António Ismael Freitas Vaz2
1School of Business Studies, Viana do Castelo Polytechnic Institute, Valença, Portugal; 2Department of Production and Systems,
University of Minho, Braga, Portugal
Received November 21st, 2009; revised May 14th, 2010; accepted May 14th, 2010.
ABSTRACT
The electric power market is changing-it has passed from a regulated market, where the government of each country had
the control of prices, to a deregulated market economy. Each company competes in order to get more cli.e.nts and
maximize its profits. This market is represented by a Stackelberg game with two firms, leader and follower, and the leader
anticipates the reaction of the follower. The problem is formulated as a Mathematical Program with Complementarity
Constraints (MPCC). It is shown that the constraint qualifications usually assumed to prove convergence of standard
algorithms fail to hold for MPCC. To circumvent this, a reformulation for a nonlinear problem (NLP) is proposed.
Numerical tests using the NEOS server platform are presented.
Keywords: Electric Power, Stackelberg Game, Nonlinear Programming, Complementarity Constrained Optimization
1. Introduction
The electric power market is in transition. Until recently,
the market was regulated by the government of each
country, and companies could on ly sell to a restrict set of
consumers.
With the deregularization, electricity industry becomes
a liberalized activity where planning and operation sch-
eduling are independent activities which are not constra-
ined by centralized procedures. On the other side, the
generator fi rms take m ore risk as they becom e responsible
for their decisions.
While in a regulated market the industry goal was to
minimize the costs - once the price was fixed-now, it is
also to maximize profit. A competition environment is
created in order to benefit the consumers through price
reduction, but ill effects can occur if the level of concen -
tration in the market grows.
In order to study the interaction of all market partici-
pants and to have a better knowledge of the market con-
ditions, firms and governments need suitable decision-
support models. The deregularization process is under
way in many countries. In 1998, the USA has begun their
transition: California, Massachusetts and Rhode Island
were the first states, but others will follow them over the
next years. Nowadays, America’s electric power industry
is highly fragmented [1].
In Europe, t he pr ocess has sta rted in the decade of 80 in
England and Wales. In the last years, the market has been
faced with fusions and merges between companies. The
directives of European Union for an electric power liber-
ality led up to increasing institutional and physical con-
nections between markets from different countries. Some
papers about studies in course, related with German,
French and The Netherlands power markets-see [2-6] for
more details-have emerged.
According to [7], there are reasons to consider electric
power as a special commodity:
All power travels over the same set of power lines, in-
dependently of the firm that generated it; this difference is
particularl y marked when the networ ks contains lo ops and
there are transmission cap acity limits; also electricity has
unique physical properties, namely Kirchhoff voltage and
current laws.
As the electricity is difficult to store, and the quantity of
power must be instantly adjusted to the demand, the
companies that lead the market could easily manipulate
the price, changing it to higher valu es, especially in peak
consumption periods. The scientific community try to find
models to predict how the prices will react to this new
market structure.
The organization of this paper is as follows: Section 2
introduces the Stackelberg game and the related concepts
and definitions of optimization. In Section 3, it is present
the formulation of the electric power problem as well as
its transformation from MPCC into a MPCC-NLP prob-

A MPCC-NLP Approach for an Electric Power Market Problem 55
lem and also the data specifying the network for the
computational experiments. Finally, the numerical results
obtained by a set of solvers are shown and the main con-
clusions are discussed in the last section.
2. Stackelberg Game and Optimization
To simulate the decision making process for defining
offered prices in a deregulated environment, it was used
the game theory, in particular the Stackelberg game. A
parallelism between this economic theory and optimiza-
tion is also addressed.
2.1 Stackelberg Game
In Stackelberg game there are two kinds of players: the
leader and the followers. The leader firm has the power
to manipulate the prices, production and expansion ca-
pacity in order to maximize its own profit and anticipates
the reaction of the rest of the player firms. The leader
uses the knowledge of the reactions in order to choose its
own optimal strategy. The follower decisions are depen-
dent on the leader strategy. The follower does not have
the perception how its decisions influence the leader
resolution.
Between followers their behaviour act like a noncoop-
erative Nash game, where all players have the same in-
formation and no one can increase their own profit
through unilateral d ecisions [8].
A Stackelberg game can be formulated as a bilevel
programming problem and therefore we introduce the
reader to it in the next subsection.
2.2 Bilevel Optimization
Definition 1 Bilevel Optimization Problem
A bilevel optimization problem is composed by a
first-level problem:
x
,y
min 1()
F
x, y
s.t. ()0gx,y  (1)
Where y, for each value of x, is the solution of the sec-
ond-level problem :
y
min 2()
F
x, y
s.t. ()0hx,y  (2)
with nx
x
IR, ny
y
IR, 12 ,:
nx+ny
F
FIR IR, :
g
nx+ny nu
I
RIR, :nx+ny nl hIR IR.
The variables x[y] are called as first [second] level
variable, g(x,y) [h(x,y)] are the first [second] level con-
straints and F1(x,y) [F2(x,y)] are the first [second] level
objective function.
A typical bilevel problem is an optimization model
whose constraints require that certain of its variables (x)
solve an optimization subproblem that dependents para-
metrically on the remaining variables (y).
Regarding with careful attention the structure of the
bilevel problem, it is possible to observe that the
first/second level of the bilevel problem corresponds to
the leader/followers players on the Stackelberg game.
A bilevel problem is convex if F2 and h are convex
functions in y for all values of x that is to say if the second
level problem is convex [9]. The problem studied in this
paper is a c onvex bile vel pr ob lem . The grea t adva ntage of
this property in bilevel optimization is th at, under certain
conditions, the second level problem can be replaced by
their own Karush-Kuhn-Tucker (KKT) conditions, and
the resulting problem is one level optimization problem
with complementarity constraints.
2.3 Mathematical Program with
Complementarity Constraints
Definition 2 MPCC Problem
Mathematical Program with Complementarity Con-
straint (MPCC) is defined as:
z
min


F
z
..
s
t


i
cz=0,i E


i
cz0,i I
12
0zz 0


(3)
where


012
,,zzzz, with the control variable 0 z

n
I
R and the state 12 ,p zz IR; F is the objective func-
tion, i c,i EI

 are the set of equality and inequality
constraints, respectively. The sets E and I are the finite
sets of indices. The objective function F and the con-
straints i c,i EI

 are assumed twice continuously
differentiable. The constraints related to complementarity
are defined with the operator  and demand that the
product of the two nonnegative quantities m ust be zero, i.e.
12ii
zz 0

,


i1,..., p.
The concept of complementarity distinguishes an MP-
CC from a standar d nonlinear optim ization problem and is
a synonymous of equilibrium, reason why this type of
problem is so popular in optimization (see [8,10,11] for
some applications in the last years).
In engineering, the MPCC problems are being used for
contact and structural mechanic problems, namely in
robotic [3,12,13], obstacle problems [14], elastohydrodi-
namic lubrification [15,16], process engineering models
[17] and traffic network equilibrium [18,19].
Applications in economics include the general equilib-
rium and game theory from which Nash and Stackelberg
game are instances [20-22].
A new field of applications is in ecological problems:
the questions related with reduction of greenhouse gas
emission rights, coalition formation and international
trade in order to negotiate the emission rights between
develop and developing countries can be also formulated

56 A MPCC-NLP Approach for an Electric Power Market Problem
as a MPCC problem [23,24].
The MPCC problem is nonsmooth mostly due to the
complementarity constraints. The optimal conditions are
complex and very difficult to verify. Besides, the feasible
set of MPCC is ill-posed since the constraint qualifica-
tions - namely, Mangasarian Fromovitz (MFCQ) and
Linear Independent (LICQ)-which are commonly as-
sumed to prove convergence of standard nonlinear pro-
gramming do not hold at any feasible point of the com-
plementarity constraints [25,26]. This implies mostly that
the multiplier set is unbounded, the active constraint
normal are linearly dependent and the linearizations of the
MPCC can become inconsistent arbitrarily close to a
solution.
The violation of constraint qualifications has led to a
number of specific algorithms for MPCCs, such as
branch-and-bound [27], implicit nonsmooth approaches
[28], piecewise SQP methods [8] and perturbation and
penalization approaches [29]. But the use of specific
solvers for MPCC is not a real solution at this time, since
these algorithms still need rather strong assumptions to
ensure convergence.
The search of new techniques and algorithms in order to
solve real problems with large dimension is still an area
with intense research. Recently, some authors suggested
solving MPCC problem by an interesting way: reformu-
lated it into an equivalent NLP problem. This formulation
allows taking advantage of certain NLP algorithms fea-
tures in order to obtain rapid local convergence. Besides,
it works like a challenge for the NLP solver, because it
allows testing its reliability and robustness, whereas the
MPCC problem has specific irregularities.
A MPCC defined in (3) can be reformulated as an
equivalent NLP problem :
Definition 3 NLP formulation of the MPCC problem
z
min


F
z
s
.t.

0
i
cz,i E

0
i
cz,i I
10z
20z
T
12 0zz

(4)
Recall that the complementarity constraint was re-
placed by a nonlinear inequality, relaxing the problem.
The transformation from a MPCC problem into a NLP
problem allows using standard NLP solvers taking to
advantage of the convergence properties of these solvers.
One can easily show that the reformulated problem has
the same properties that the previous one, including con-
straint qualifications and second-order conditions, which
means that the violation of MFCQ is still a reality. How-
ever, in the last few years, some studies show that strong
stationarity is equivalent to the KKT conditions of the
MPCC-NLP problem [30,31]. This fact has advantages
because strong stationarity is a useful and practical com-
putation characterization, once it is relatively easy to find
a stationary point in a NLP solver, under reasonable as-
sumptions.
3. The Electric Power Market Problem
The problem describe d in this pa per is based on the model
proposed in [32]. It is a competitive power market, for-
mulated as an oligopolistic equilibrium model.
There are a number of generator firms, each owing a
given number of units. These make an hourly bid to an
Independent System Operator (ISO). The ISO, taking in
consideration the network, solves a social welfare maxi-
mization problem, announces a dispatch for each bidder
and possibly distinct prices at each node. It decides how
much power to buy fr om gener ators an d how much power
to distribute to consumers and what prices to charge. All
these decisions are made with the optimal power flow
(OPF) in mind.
In spite of the fact that the ISO expects the bid to be a
reflex of the true costs, the reality is different: the units,
generally, increase their own bid, without the knowledge
of the outside world, as the Figure 1 shows. This strategy
has as main goal the increase of the units’ profit.
The leader generator first decides and takes as input all
the perceptions and information that it could have about
the market (including predictable bids of the other firms,
demand and supply functions) and it maximizes its profit
inside a set of spatial price equilibrium constraints and
Kirchhof f’s vo ltage and c ur ren t laws. The followers firm s
make their own decisions taking into account the leader
decision.
3.1 Formulation
In [32] the electric power market was formulated as a
bilevel problem. In the first level-the leader level-the
parameter related with the bid curve corresponds to the
first level variable. In the second level-the follower level -
there is a simulation of the conjectures of the market
promoted by ISO and can be described as a commodity
spatial price equilibrium problem. The model tries to find
the optimal bid for each company.
Figure 1. Marginal cost and bid curves.

A MPCC-NLP Approach for an Electric Power Market Problem 57
Next we introduce the notation used in the mathe-
matical formulation:
Indices:
i node in the network
ij arc from node i to node j
m number of Kirchhoff voltage loops in the net-
work
Sets:
N set of all nodes
A set of all arcs
Sf set of generator nodes under control of leader
firm f
P set of all generators nodes
D set of all demand nodes
L set of Kirchhoff’ voltage loops m
Lm set of ordered arcs (clockwise) associated with
loop m
Recall that, a node can be, simultaneously a generator
and a consumer, so P and D are not necessarily disjoint
and their union could be a proper subset of N. The
uniqueness of the net flow on each arc is ensured by the
Kirchhoff’s laws in the linearized DC models and, con-
sequently, the number of (independent) loops is #A – #N +
1 (where #X is the set X cardinality).
Parameters:
ii
a,b intercept and slope of supply function
(marginal cost) for the generator at node
iP
ii
c, d intercept and slope of demand function for
consumer at node iD
i
αi α upper bound of the bid for the unit at node
f
iS
i
S
Q upper bound of production capacity for the
unit at node iP
ij
T maximum transmission capacity on arc
ij A
ij
r reactance on arc ij A
ijm
s
1corresponding to the orientation of the
arc ij A in loop mL
(+1 if ij has the sam e orientation as t he loop
m)
First-Level decision variable
i
α bid for the unit at node iP
In this model, it is assumed that the generate firms can
only manipulate α (t he intercept in the bid function) and
not the slope b, due to market and optimization as-
sumptions.
Let i α be fixed for the competitive firms (i.e. i α
fixed
f
iP\S ) and variables for the leader firms (i.e.
i
α variable
f
iS ).
Primal variables in the second-level:
i
S
Q
vector defined by quantity of power gener-
ated by the unit at node i
(ii
SiiS
Qa+bQ if iP and 0
i
S
Q

if
iP)
i
D
Q
quantity of power demanded at node i
(ii
D
iiD
Q=c dQ

if iD and 0
i
D
Q=if
iD)
ij
T matrix defined by MW transmitted from
node i to node j
Dual variables in the second-level
i
λ
marginal cost at node i
i
μ
marginal v alu e of generation capacity for unit
at node i
ij
θ marginal value of transmission capacity on arc
ij
m
γ shadow price for Kirchhoff voltage law for
loop m
Next, it is defined the second-level convex quadratic
problem. The objective function is related with the
maximization of social welfare:
max 22
11
22
ii ii
iDiDiS iS
iD iP
cQ dQαQbQ


 


 (5)
This function reports a solution where the firms
maximize their profits and the consumers maximize the
utility of the product.
The following constraints report to a spatial price equi-
librium plus a constraint due to Kirchhoff voltage law.
 Nonnegative demand variables:
0,
i
D
Q Di

(6)
 Lower and upper bounds for transmission variables:
0,
ij ij
TTij A

(7)
 Minimum and maximum capacity of production:
0,
ii
SS
QQ iP

(8)
 Conservation constraints:
::
0
ii
DSij ij
jij Ajij A
QQT T




 (9)
 Kirchhoff voltage law:
0
ijm ijij
ij Lm
srT



(10)
If in Equation (8), by economic reasons, the minimum
production level could not be zero , it is possi ble t o change
the lower bound and still us e the same model.
The description of the first level of the electric power is
complete by taking into account that for the follower firms
the bids are already fixed. The determination of the
dominant company profit consists in finding a bid vector


:
f
if
ααiS

, a vector of supplies S
Q, a vector of
demands
D
Q and a vector of transmission capacities T,
by solving the following maximization problem.
Maximize 2
(, )2
f
i ii
i
iS
f SiS iSS
b
QQaQQ
 






(11)

58 A MPCC-NLP Approach for an Electric Power Market Problem
s.t. 0,
ii f
iS

  
where S Q,
D
Q and T for each value of

:
iiP
 , are
the solution of the second-level problem (5-10).
It is provided in [33] that, for each vector

, there
exists a unique globally optimal solution of the quadratic
problem above.
But, solving a bilevel problem is not an easy task. So,
the approach is to replace the ISO’s lower-level optimi-
zation problem by its stationa ry conditions that results in a
system of equilibrium constraints. To write the above
information into a vector-matrix notation, it is necessary
to introduce two additional matrices.
Let  be the matrix which give us the information
about the pair (node, arc) in the electric network:
1,
1, or
0,
il
iflijAforsome jN
iflijAfsome jN
other values
 

 



(12)
Let R be the matrix (arc, cycle) related with the reac-
tance coefficients: ,
0,
ijm ijm
ijm
s
rif ijL
Rotherwise



 (13)
So, the Karush-Kuhn-Tucker (KKT) optimality condi-
tions of the lower problem are:
0SS QQ  0


0S Q 


0
S
λ+μ+α+diagbQ
0
D
Q 


D0λc+α+diag d Q
 
(14)
0θ


0TT
0T


0
Tλ+θ+Rγ
free

0
DS
QQ T
free

0
T
RT
(14)
where μ,θ,
λ
and

are the dual variables. The nota-
tion diag(w) represents the diagonal matrix whose di-
agonal entries are the components of the vector w.
Then, the second-level problem (5-10) can be replaced
by the KKT conditions (14) and the MPCC problem is
obtained by joining (11) and (14 ).
For computational reasons the objective function needs
to be reformulated, since it is neither convex nor concave
due to the term i
iS
λQ. The equivalent objective function
for solve the maximization of the leader firm profit is:


fS
,Q



22
2
iii i
f
i
iD iDiSS
iD iS
b
cQ dQaQQ


 





2
iii
f
ijijiSiSi S
ijAi P\S
θTμQ+aQbQ

 
 (15)
3.2 Data
The electric power network includes a circuit with 30
nodes, which 6 are nodes with generators-3 for the leader
firm A and the 3 rem aining for the follower firm B-and 21
are demand nodes. Con necting t he nodes the re are 41 a rcs
and 12 loops. Figure 2 shows a scheme that provides all
the necessary information.
Figure 1. Electric Network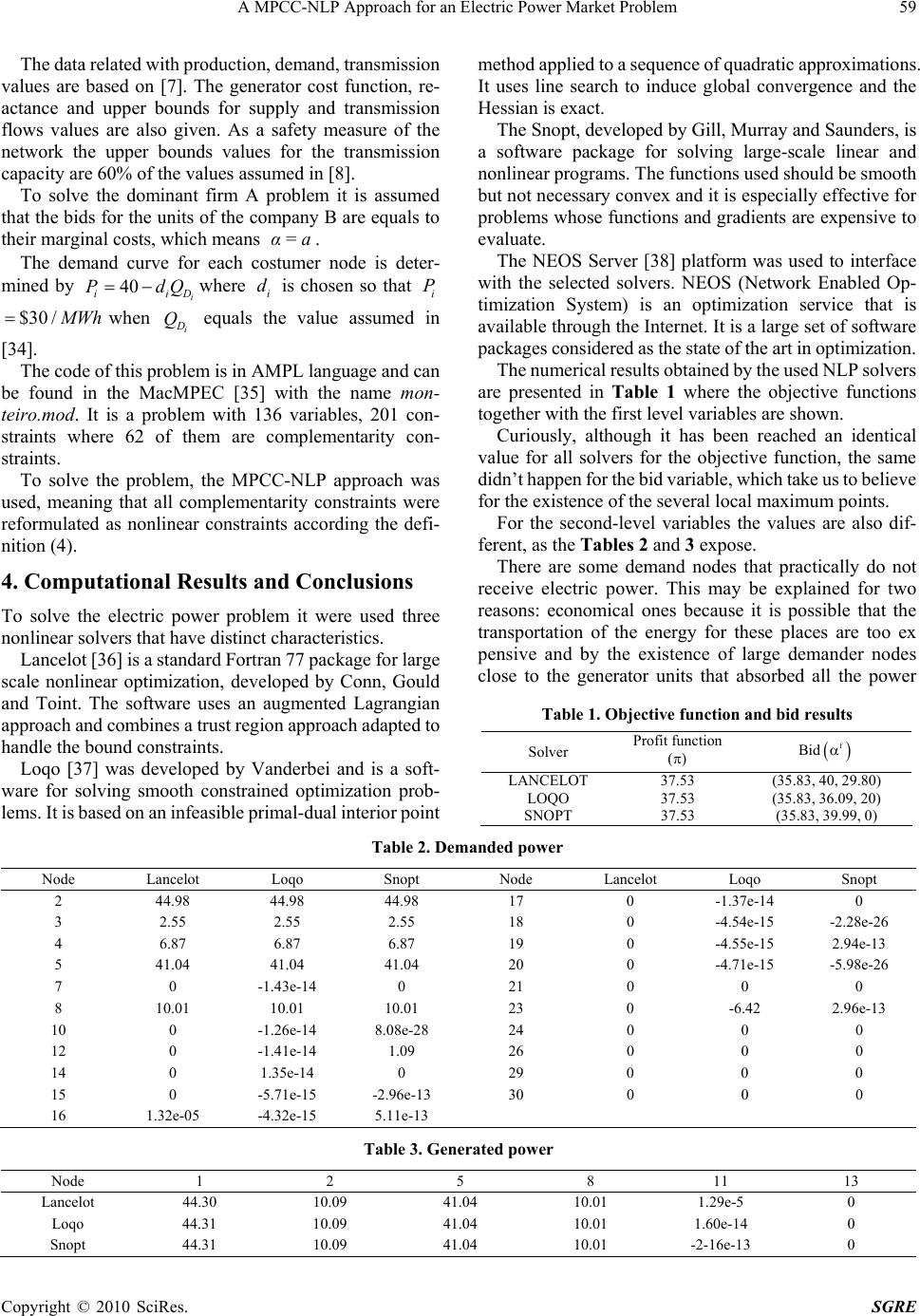

A MPCC-NLP Approach for an Electric Power Market Problem 59
The dat a related with pr oduction, dem and, transmissi on
values are based on [7]. The generator cost function, re-
actance and upper bounds for supply and transmission
flows values are also given. As a safety measure of the
network the upper bounds values for the transmission
capacity are 60% of the values assumed in [8].
To solve the dominant firm A problem it is assumed
that the bids for the units of the company B are equals to
their marginal costs, which means α=a.
The demand curve for each costumer node is deter-
mined by 40 i
iiD
PdQ where i d is chosen so that i P
$30 /
M
Whwhen i
D
Q equals the value assumed in
[34].
The code of this problem is in AMPL language and can
be found in the MacMPEC [35] with the name mon-
teiro.mod. It is a problem with 136 variables, 201 con-
straints where 62 of them are complementarity con-
straints.
To solve the problem, the MPCC-NLP approach was
used, meaning that all complementarity constraints were
reformulated as nonlinear constraints according the defi-
nition ( 4) .
4. Computational Results and Conclusions
To solve the electric power problem it were used three
nonlinear solvers th at have distin ct characteristics.
Lancelot [36] is a standard Fortran 77 package for larg e
scale nonlinear optimization, developed by Conn, Gould
and Toint. The software uses an augmented Lagrangian
approach an d com bines a trust regi on ap proach ada pted to
handle the bound constraints.
Loqo [37] was developed by Vanderbei and is a soft-
ware for solving smooth constrained optimization prob-
lems. It is based o n an infeasibl e primal-dual interior point
method appl ied to a sequence of quadratic ap proximati ons.
It uses line search to induce global convergence and the
Hessia n is exact.
The Snopt, developed by Gill, Murray and Saunders, is
a software package for solving large-scale linear and
nonlinear program s. The fu ncti ons use d shoul d be sm ooth
but not necessary convex and it is especially effective for
problems whose functions and gradients are expensive to
evaluate.
The NEOS Server [38] platform was used to interface
with the selected solvers. NEOS (Network Enabled Op-
timization System) is an optimization service that is
available through the Internet. It is a large set of software
packages considere d as the state of the art in optim ization.
The numerical results obtained by the used NLP solvers
are presented in Table 1 where the objective functions
together with the first level variables are shown.
Curiously, although it has been reached an identical
value for all solvers for the objective function, the same
didn’t ha ppen for the bid variable, whic h take us to bel ieve
for the existence of the several local maximum points.
For the second-level variables the values are also dif-
ferent, as the Tables 2 and 3 expose.
There are some demand nodes that practically do not
receive electric power. This may be explained for two
reasons: economical ones because it is possible that the
transportation of the energy for these places are too ex
pensive and by the existence of large demander nodes
close to the generator units that absorbed all the power
Table 1. Objective function and bid results
Solver Profit function
()

Bid

f

LANCELOT 37.53 (35.83, 40, 29.80)
LOQO 37.53 (35.83, 36.09, 20)
SNOPT 37.53 (35.83, 39.99, 0)
Table 2. Demanded power
Node Lancelot Loqo Snopt Node Lancelot Loqo Snopt
2 44.98 44.98 44.98 17 0 -1.37e-14 0
3 2.55 2.55 2.55 18 0 -4.54e-15 -2.28e-26
4 6.87 6.87 6.87 19 0 -4.55e-15 2.94e-13
5 41.04 41.04 41.04 20 0 -4.71e-15 -5.98e-26
7 0 -1.43e-14 0 21 0 0 0
8 10.01 10.01 10.01 23 0 -6.42 2.96e-13
10 0 -1.26e-14 8.08e-28 24 0 0 0
12 0 -1.41e-14 1.09 26 0 0 0
14 0 1.35e-14 0 29 0 0 0
15 0 -5.71e-15 -2.96e-13 30 0 0 0
16 1.32e-05 -4.32e-15 5.11e-13
Table 3. Generated power
Node 1 2 5 8 11 13
Lancelot 44.30 10.09 41.04 10.01 1.29e-5 0
Loqo 44.31 10.09 41.04 10.01 1.60e-14 0
Snopt 44.31 10.09 41.04 10.01 -2-16e-13 0

60 A MPCC-NLP Approach for an Electric Power Market Problem
produced.
It has been s hown t hat M PCC-NL P appr oach should be
considered to solve real problems.
As future work it is proposed the study of this problem
developed as a nash model, where both firms compete at
the same level and with the same market information.
EFERENCES
[1] M. Willrich, “Electricity Transmission Policy for America:
Enabling a Smart Grid, End to End,” The Electricity
Journal, Vol. 22, No. 10, 2009, pp. 77-82.
[2] “Third Benchmarking Report on the Implementation of
the Internal Electricity and Gas Markets,” Tech Republic
1, Commission Draft Staff Paper, March 2004.
[3] B. F. Hobbs and F. A. M. Rijkers, “Strategic Generation
with Conjectured Transmission Price Responses in a
Mixed Transmission Pricing Sy stem,” IEEE Transmissions
on Power Systems, Vol. 19, No. 2, 2004, pp. 707-879.
[4] Y. Smeers, “How Well Can Measure Market Power in
Restructured Electricity Systems,” Tech Republic, Uni-
versity Catholique De Louvain, November 2004.
[5] S. A. Gabriel and F. U. Leuthold, “Solving Discretely-
Constrained MPEC Problems with Applications in Electric
Power Markets,” Energy Economics, Vol. 32, No, 1,
2010, pp. 3-14.
[6] M. Crappe, “Electric Power Systems,” Wiley-ISTE, 2009.
[7] C. B. Metzler, “Complementarity Models of Competitive
Oligopolistic Electric Power Generation Markets,” Master’s
Thesis, The Johns Hopkins University, 2000.
[8] Z.-Q. Luo, J.-S. Pang and D. Ralph, “Mathematical
Programs with Equilibrium Constraints,” Cambridge
University Press, Cambridge, 1996.
[9] L. N. Vicente and P. H. Calamai, “Bilevel and Multilevel
Programming: a Bibliography Review,” Journal of Global
Optimization, Vol. 5, No. 3, 1994, pp. 291-306.
[10] S. Dempe, “Annotated Bibliography on Bilevel Program-
ming and Mathematical Programs with Equilibrium Con-
straints,” Optimi zation, Vol. 52, No. 3, 2003, pp. 333-359.
[11] M. C. Ferris and J. S. Pang, “Engineering and Economic
applications of Complementarity Problems,” SIAM Re-
view, Vol. 39, No. 4, 1997, pp. 669-713.
[12] M. F. Ferris and F. Tin-Loi, “Limit Analysis of Frictional
Block Assemblies as a Mathematical Program with Com-
plementarity Constraints,” International Journal of Mech-
anical Sciences, Vol. 43, No. 1, 2001, pp. 209-224.
[13] J. S. Pang, “Complementarity Problems,” In: R. Horst and
P. Pardalos, Eds., Handbook in Global Optimization, K.
A. Publishers, Boston, 1994.
[14] J. F. Rodrigues, “Obstacle Problems in Mathematics Phy-
Sics,” Elsevier Publishing Company, Amsterdam, 1987.
[15] M. C. Ferris and F. Tin-Loi, “On the Solution of a
Minimum Weight Elastoplastic Problem Involving Dis-
placement and Complementarity Constraints,” Computer
Methods in Applied Mechanics and Engineering, Vol.
174, No. 1-2, 1999, pp. 107-120.
[16] K. P. Oh and P. K. Goenka, “The Elastohydrodynamic
Solution of Journal Bearings under Dynamic Loading,”
Transactions of American Society of Mechanical En-
gineers, Vol. 107, No. 3, 1985, pp. 389-395.
[17] A. U. Raghunathan and L. T. Biegler, “Mathematical Pro-
grams with Equilibrium Constraints (Mpecs) in Process
Engineering,” Tech Republic, CMU Chemical Engine-
ering, November 2002.
[18] O. Drissi-Kaitouni and J. Lundgren, “Bilivel Origin-Dest-
ination Matrix Estimation Using a Descent Approach,”
Tech Republic, Linköping Institute of Technology, De-
part-ment of Mathematics, Sweden, 1992.
[19] M. Stohr, “Nonsmooth Trust Region Methods and their
Applications to Mathematical Programs with Equilibrium
Constraints,” Shaker Verlag, Aachen, 2000.
[20] C. Ballard, D. Fullerton, J. B. Shoven and J. Whalley, “A
General Equilibrium Modelfor Tax Policy Evaluation,”
National Bureau of Economic Research Monograph, Chi-
cago, 1985.
[21] H. Ehtamo and T. Raivio, “On Aapplied Nonlinear and
Bilevel Programming for Pursuit-Evasion Games,” Journal
of Optimization Theory and Applications, Vol. 108, No.
1, 2001, pp. 65-96.
[22] J. V. Outrata, “On Necessary Optimal Conditions for
Stackelberg Problems,” Journal of Optimization Theory
and Applications, Vol. 76, No. 2, 1993, pp. 305-320.
[23] J. C. Carbone, C. Helm and T. F. Rutherford, “Coalition
formation and International Trade in Greenhouse Gas
Emission Rights,” MIMEO, the Sixth Annual Conference
on Global Economic Analysis, Scheveningen, The Hague,
The Netherlands, June 12-14 2003.
[24] G. Hibino, M. Kainuma and Y. Matsuoka, “Two-Level
Mathematical Programming for Analysing Subsidy Options
to Reduce Greenhouse-Gas Emissions,” Tech Republic,
Laxenburg, 1996.
[25] M. Kocvara and J. V. Outrata, “Optimiz ation Problems w i t h
Equilibrium Constraints and their Numerical Solution,”
Mathematical Programs, Series B, Vol. 101, No. 1, 2004,
pp. 119-149.
[26] H. S. Rodrigues and M. T. Monteiro, “Solving Mathe-
matical Program with Complementarity Constraints
(MPCC) with Nonlinear Solvers,” Recent Advances in
Optimization, Lectures Notes in Economics and Mathe-
matical Systems, Springer, Berlin, Part 4, 2006, pp. 415-
424
[27] J. F. Bard, “Convex Two-Level Optimization,” Mathema-
tical Programming, Vol. 40, No. 1, 1988, pp. 15-27.
[28] J. Outrata, M. Kocvara and J. Zowe, “Nonsmooth App-
roach to Optimization Problems with Equilibrium Cons-
traints,” Kluwer Academic Publishers, Dordrecht, 1998.
[29] M. C. Ferris, S. P. Dirkse and A. Meeraus, “Mathematical
Programs with Equilibrium Constraints: Automatic
Reformulation and Solution via Constrained Optimi-
zation,” Tech Republic, Oxford University Computing
Laboratory, July 2002.
[30] H. Scheel and S. Scholtes, “Mathematical Programs with

A MPCC-NLP Approach for an Electric Power Market Problem 61
Complementarity Constraints: Stationarity, Optimality and
Sensitivity,” Mathematics of Operations Research, Vol.
25, No. 1, 2000, pp. 1-22.
[31] S. Scholtes, “Convergence Properties of a Regularization
Scheme for Mathematical Programs with Complementarity
Constraints,” SIAM Journal Optmization, Vol. 11, No. 4,
2001, pp. 918-936.
[32] B. F. Hobbs, C. B. Metzler and J.-S. Pang, “Strategic
Gaming Analysis for Electric Power Systems: An MPEC
Approach,” IEEE Transactions on Power Systems, Vol.
15, No. 2, 2000, pp. 638-645.
[33] V. Krishna and V. C. Ramesh, “Intelligent agents in Neg-
otIations in Market Games, Part 2: Application,” IEEE
Transactions on Power Systems, Vol. 13, No. 3, 1998, pp.
1109-1114.
[34] O. Alsa and B. Scott, “Optimal Load Flow with Steady-
State Security,” IEEE Transactions on Power Systems,
Vol. 93, No. 3, 1973, pp. 745-751.
[35] S. Leyffer, Macmpec, 2010. http://www.mcs.nl.gov/
leyffer/macmpec
[36] Lancelot, 2010. http://www.numerical.rl.ac.uk/lancelot/blurb.
html
[37] H. Benson, A. Sen, D. Shano and R. Vanderbei, “Interior-
Point Algorithms Penalty Methods and Equilibrium Prob-
lems,” Tech Republic, Operations Research and Financial
Engineering Princeton University, October 2003.
[38] NEOS, 2010. http://www-neos.mcs.ang.gov/neos