Advances in Pure Mathematics, 2012, 2, 190-194
http://dx.doi.org/10.4236/apm.2012.23026 Published Online May 2012 (http://www.SciRP.org/journal/apm)
Tensor Product of Krammer’s Representations of the
Pure Braid Group, P3
Hassan A. Tarraf, Mohammad N. Abdulrahim
Department of Mathematics, Beirut Arab University, Beirut, Lebanon
Received December 27, 2011; revised February 17, 2012; accepted February 25, 2012
ABSTRACT
We consider the complex specializations of Krammer’s representation of the pure braid group on three strings, namely,
where q and t are non-zero complex numbers. We then specialize the indeterminate t by one
and replace

3
,:Kqt P
 
3, ,

GL

,1
K
q by

K
q
 

33
123
:KqKq PGL
for simplicity. Then we present our main theorem that gives us sufficient conditions
that guarantee the irreducibility of the tensor product of two irreducible complex specializations of Krammer’s repre-
sentations .
Keywords: Braid Group; Pure Braid Group; Magnus Representation; Krammer’s Representation
1. Introduction
Let Bn be the braid group on n strings. It has many kinds
of linear representations. The earliest was the Artin rep-
resentation, which is an embedding


BAutF

nn
.
Applying the free differential calculus to elements of
n
A
ut F sometimes gives rise to linear representations
of Bn and its normal subgroup, the pure braid group de-
noted by Pn. The Lawrence-Krammer representation
named after Ruth Lawrence and Daan Krammer arises
this way. Krammer’s representation is a repr esentation of
the braid group Bn in



0
Aut V


 , wher
11
,,t q

GL me

12mnn and V0 is the free module of rank m over
11
,
.
tq


It

is denoted by

,.
K
qt For simplicity, we
tead of

,.
write K ins
K
qt In previs work, we con-
sidered Krammer’s reprens of B3 and P3 and we
specialized the indeterminates to non zero complex
numbers. We then found necessary and sufficient condi-
tions that guarantee the irreducibility of such representa-
tions. For more details, see [1,2]. Note that in a previous
work of Abdulrahim and Al-Tahan [2], a necessary and
sufficient condition for the irreducibility of Krammer’s
representation of degree three was found. However, in
our cu rrent work, w e are dealing with a representation of
higher degree (degree nine) and which also has two in-
determinates. This made our work seem more difficult.
For this reason, we had to be satisfied in this current
work with only a sufficient condition for irreducibility,
so we fell short of finding a necessary and sufficient
condition for irreducibility. To make computations easier,
we had to specialize the indeterminate t by one in order
to have a one parameter complex specialization.
In Section 2, we introduce the pure braid gr
ou
sentatio
oup and
K
2. Definitions
aid group on n strings, Bn, is the
rammer’s representation. In Section 3, we present our
main theorem, Theorem 1, which gives sufficient condi-
tions that guarantee the irreducibility of the tensor prod-
uct of two irreducible complex specializations of Kram-
mer’s representations of P3. In this way, we will have
succeeded in constructing a representation of the pure
braid group, P3, of degree nine and which is also irre-
ducible.
Definition 1. [3] The br
abstract group with presentation
111
,,
n iii
 
 11
for 1,2, ,2,.
if 1
iii
n
ij ji
in B
ij
 
















The generators 11
,,
n




 are called the standard
ge Pure braid group on n strands, de-
no
ith item o
i. It is generated by the generators ij
nerat ors o f B n.
Definition 2. The
ted by Pn, is the kernel of the group homomorphism
.
nn
BS It consists of those braids which connect the
f the left set to the ith item of the right set for all
, 1<ijn
A
C
opyright © 2012 SciRes. APM

H. A. TARRAF, M. N. ABDULRAHIM 191
where 211 1
121121
.
ijjjiiijj
A  

 

Definition 3. [4] The image of ator each Artin generunder Krammer’s representation with respect to


1,
ij ijn
x  the free basis of V0, is written as follows:

2,1
,,1
,,1;
1,,;
,;
,1;
1,1;
r 1;
1.
kk
ik ik
tq xikjk
qxqxj ki k
ik
j
kj
 




1
,, 1
,1 1,
,
,1,
,
2
,,1
1, 1
1,
1,
, o
1,
ki
ik kk
kkk j
kij
kjk j
ij
ki
ij kk
xt q qxjk
tqqxqxik k
Kx
xqx ik
x
ijk
xtqq xikk







 
 

 
k ij
j



 







Now, we
 







determine Krammer’s representation



11
,:3,,Kqt PGLtq



3
using the Magnus representation of subgroups of the

automorphisms group of free group with

12nn gen-
erators, where 11 ,tq



 is the ring o poly- f Laurent
variables.
 

24
23
2
00
11,
11 1
tq
tq qqqq
tq qqqq


 





 

23
24
2,3 24
11 1
11
00
qq qqtqq
KAqqtq q
tq

 

 



and

 
nomials on twoThe images of the generators
under Krammer’s representation are as follows

1,2
KA



 

2
23
22
2
11
1
111 ,
111
qtqq
qqq t
KAtqqtqtq qqqm
tqqtq qqtqn















  
4
22 2
12211 11mqqqtqqqqqt

 

 

2
11111 .nqqtqqtq



Specializing the indeterminates q and t to nonzero
co
if
q
For mo
th
1,3
where
 
nd a
mplex numbers gives a representation
 
3
,: 3,Kqt PGL which is irreduci
23
t
ble if and only
3 2
1 ,1,1,1,1 and1.tqtq tqtq
re details, see [2]. indeterminate t by one. We We now specialize the
en write

K
q for

,1 .Kq So,


K
q is irreduci-
ble if and only
32
1and 1.qq


By replacing t by one, the matrices of the generators
be
 

4
3
2
00
11,
11 1
q
qqq qq
qqqq q


 






23
4
4
11 1
11
00
qqqqqq
qq qq
q

 

 





 



 

2
23
22
2
111
111 ,
111
qqq qqq
qAqqqqq qqm
qqqq qqn






 




K
if
come as follows:

 
1,2
qA K
 
2,3
qAK
and
1,3

H. A. TARRAF, M. N. ABDULRAHIM
192
where
 

1 1qqq

 

and

2
11 .qq



In our work, we consider the tensor product of two ir-
ducible complex specializations of Krammer’s repre-
tions of the pure braid group, namely,
 
12
.

4
22
1221 1mqqqqq 

111nqqq 
re
senta
K
qKq
3.
the iduciiof two ire-
ducible complexspecializations of Krammer’s represen-
tations of the pure braid group on three strings, P3.
Theorem 1. For

2
1, 2
()qq  , the tensor product of
two irreducible complex specializations of Krammer’s
representations
Sufficient Conditions for Irreducibility
In this section, we find sufficient conditions that guaran-
teerreblity of the tensor product



33
123
:KqKq PGL is
2 121
4 3
,1,qqqq
irreducible if
44 4424 42 24
12121 2
424 3
1212 12
1, 1,,
,1,1,1,1.
qqqqq q
qqqqq q
 

Proof. For simplicity, we write ij
A
to mean




12ijij.
A
qAq23 A
by an invertib Let us diagonalize the matrix le matrix T, and conjugate the matrix 12 A
by T. The invertible matrix T is given by


1212
1qa qqq





2 1
2
22 2
1112 1112
22 222
112
2
0 0
11
111
1111
000001 1
001000
00100100
000000001
aqc cqac
d dq
qqqqqqqq
qc c
qqq
bbdde
b
qc
d
 

 
 




,











2
12 2 2
1
22
12
1
1
11
1
qqq q
qq
qa

 






11
11qa q a





0000

11bq




T
0
0





where
 



22
12
1
22
11
22
1112 2
222
212
1
,1, ,
111
11
1
1and
(1 )11
qq
abqc
qq
qqqqq
dq e
qqq


 
 

Diagonalizing 23 A by T, we get that
2
14
12
222
2
2
2
2
.
q
q
1 242
24
44
12
1000 00 0 00
0000 000 0
0000 000 0
0000 000 0
.0000 0 00
0000 00 00
0 0
0
0
q
q
q
qq
qq
qq














23 0

A
12 4
2
12
0
000 00
0000 00 0
0000 00 0
q
qq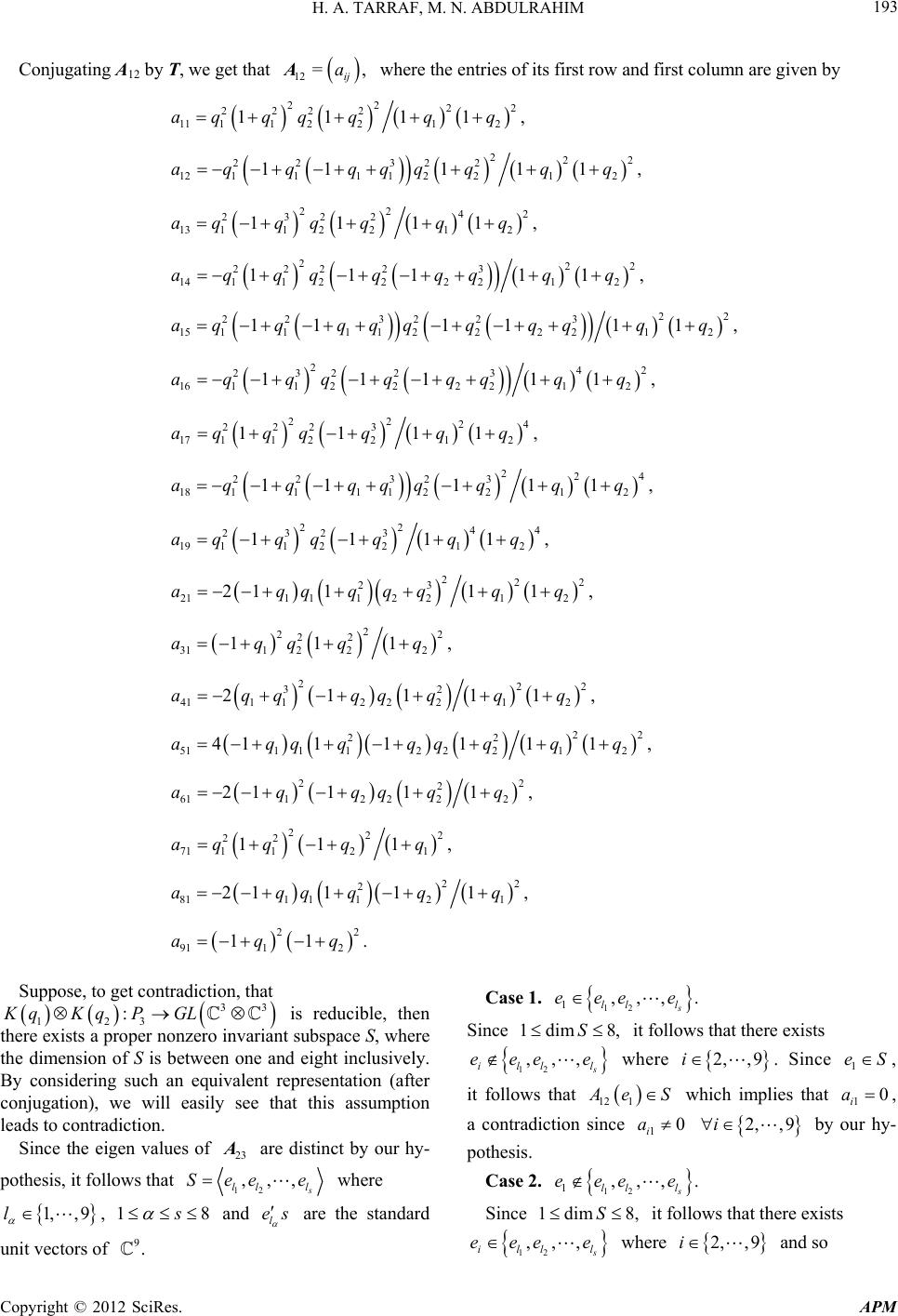

H. A. TARRAF, M. N. ABDULRAHIM 193
Conjugating A12 by

12 =, ij
aA where the entries of its first row and first column are given by

T, we get that

22
2222
111122
11aq qq q 22
1 2
11,q q

  
2
22 322
12111122
11 1aq q qqqq  22
12
11,q q


22
2322
13 1122
11aqqq q 42
1 2
11,q q

 

222
12
11,q q
22 2 23
14112222
111aqqq q qq  








22
2322 3
15112222 12
1111 11,aqqqqqqq qq
2
11
q
 


242
2322 3
16112222 12
111 1,aq qq q qqq q 
 

1
22
24
2223
17 112212
1111,aq qqqqq




224
23
22 12
1 11,qq q 
22 3
181111
11aq qqqq  


22
44
2323
191122 12
1111aq qq qqq ,



2
23
211 1122
21 1aqqqq 22
1 2
11,qqq



2
22
22

31 1 222
111,aqqqq



2
32
22
2 2212
21111,aqq qqqqq 


41 1 1





22
22
2 2212
1111,qqqqqq 
51 1 11
41 1aqq 




22
2,q
2
61 12 22
2111 1aqqqq  


222
22
71 1121
111,aq qqq



22
1
1 ,qq

.q
Supp

Kq
there ex
the dimd eight inclusively.
By convalent representation (after
conjugation), we will easily see that this assumption
leads to contradiction.
Since the eigen values of 23
A are distinct by our hy-
2
81 1 112
211 1aqqq 

22
91 1 2
11aq

ose, to get contradiction, that


33
123
:Kq PGL
is reducible, then
ists a proper nonzero invariant subspace S, where
ension of S is between one an
sidering such an equi
pothesis, it follows that 12 ,,,
s
ll l
See e where

1,, 9

, 18sl

 and l es

 are the standard
un
Case 1.

12
1,, .
s
ll l
eeee
Since 1dim8,S
it vectors of 9.
,
 it follows that there exists



12
,,,
s
ill l
ee e where

2, ,9i. Since 1 eSe

,
it follows that


12 1
A
eS which implies that 10
i
a


,
a contradiction since 10
i
a



2, ,9i  by our hy-
pothesis.
Case 2.


12
1,,,.
s
ll l
eeee
Since 1dim8,S it follows that there exists



12
,,,
s
ill l
eee e where

2,i

,9 and so

H. A. TARRAF, M. N. ABDULRAHIM
194

12 1
A
eS which implies that 10
i
a, a contradiction
since 10
i
a

2, ,9i .
REFERENCES
[2] M. N. Abdulra. Al-Tahan, “Krammer’s Rep-
resentation of the Pure Braid Group, tional
Journa
010, 20, Article ID 806502. doi:10.1155/2010/806502
[1] . A
Repres
f Mathematics and S
No. 4, 2008, pp. 213-216.
doi:10.3844/jmssp.2008.2
M. N. Abdulrahim and Ml-Tahan, “Complex Spe-
cializations of Krammer’s entation of the Braid
Group, B3,” Journal otatistics, Vo
13.216
l. 4,
him and MP,” Interna
3
l of Mathematics and Mathematical Sciences, Vol.
2 10
[3] J. S. Birman, “Braids, Links and Mapping Class Groups,”
Annals of Mat, Princeton Univer-
sity Press, Prin
hematical Studies, No. 8
ceton, 1974.
[4] D. Krammer, “Braid Groups Are Linear,” Annals of M ath e-
matics, Vol. 155, No. 1, 2002, pp. 131-156.
doi:10.2307/3062152