International Journal of Geosciences, 2012, 3, 321-328
http://dx.doi.org/10.4236/ijg.2012.32034 Published Online May 2012 (http://www.SciRP.org/journal/ijg)
Correlation between Solar Semi-Diameter and
Geomagnetic Time Series
Eugênio Reis Neto1,2, Vitor Hugo Alves Dias1, Andrés Reinaldo Rodriguez Papa1,3*,
Alexandre Humberto Andrei1,4, Jucira Lousada Penna1, Irineu Figueiredo1,3,
Sérgio Calderari Boscardin1, Victor de Amorin d’Ávila1,3
1Observatório Nacional, Rio de Janeiro, Brazil
2Museu de Astronomia e Ciências Afins, Rio de Janeiro, Brazil
3Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brazil
4Observatório do Valongo/UFRJ, Rio de Janeiro, Brazil
Received December 19, 2011; revised February 16, 2012; accepted March 17, 2012
ABSTRACT
We study the correlation between geomagnetic and solar semi-diameter measurements made at two of our ground sta-
tions (Vassouras and Rio de Janeiro, Brazil). The study comprises the period from March 1998 to November 2003, for
which daily means were compared. Both series describe correlated, but different, phenomena and, consequently, before
a correlation study, an individual analysis of each data set was necessary. One of the motivations of the present work
was to further explore the correlation with lags found between the solar semi-diameter and some solar activity estima-
tors, which supports the probabilistic forecasting of the solar activity and hence, of the solar driven geomagnetic varia-
tions.
Keywords: Solar Diameter; Geomagnetic Series; Correlation; Time Series
1. Introduction
The study and forecasting of catastrophic natural pheno-
mena has always been an attractive and challenging area
which has called the attention of many scientists along
the years (see, for example, the works by Sornette [1],
Papa and collaborators [2], Papa and Sosman [3], Merrill
and collaborators [4], Dias and collaborators [5] and re-
ferences there in). Examples of those phenomena are the
magnetic storms which are periods, lasting between one
and three days, during which the geomagnetic field su-
ffers violent variations. While the total magnetic field
that can be measured at the Earth’s surface is around
40,000 nT, magnetic storms perturbations range from
400 to 700 nT in the severest cases. This amount is only
1% to 2% of the total amplitude. Nevertheless, they can
relevantly affect telecommunications, energy transmission
lines and, supposedly, the human physiology [6,7] while,
at the same time, are useful for some scientific, techno-
logical and, maybe, forecasting methods (see the works
by Gleisner and collaborators [8], Pulinets & Boyarchuk
[9] and their references).
The bulk of solar light and heat received by the Earth
is released from the solar photosphere. Though virtually
all the energy is produced in the solar core through the
proton-proton fusion chain, it undergoes a lengthy path-
way, across the radiation zone and up to the convective
zone, during a million years process, to finally reach
what is purposely called the solar photosphere.
The solar energy is one of the major driving inputs for
terrestrial climate. Some evidences of correlation exist
between surface temperature changes and solar activity.
It is then important to know on what time scales the solar
irradiance and other fundamental solar parameters, like
the diameter, vary in order to better understand and access
the origin and mechanisms of the terrestrial climate
changes.
Global effects, such as diameter changes, large conve-
ctive cells, the differential rotation of the Sun’s interior
and the solar dynamo at the base of the convective zone
can probably produce variations in the total irradiance or,
at least, correlate with these variations associated, during
maximum, with the changing emission of bright faculae
and with the magnetic network [10].
In recent years evidence has accumulated showing that
flares and CMEs are different observational manifesta-
tions of a single process—the destabilization and reor-
ganization of magnetic fields at active region spatial
scales. Neupert and collaborators [11] and Zhang &
Wang [12] have clearly shown the connection between
*Corresponding author.
C
opyright © 2012 SciRes. IJG

E. R. NETO ET AL. 322
the two in a couple of events. We will present a further
1000 1500 2000 2500 3000
956.0
956.5
957.0
957.5
958.0
958.5
959.0
959.5
960.0
960.5
961.0
961.5
962.0
well-observed example showing the same connection.
For this we trace the correlation between peaks of vari-
ation of the flare counts against the peaks of variation of
the solar diameter and of the intensity of the geomagnetic
field measured by two of our stations. Although the ob-
servations are very detailed, they still do not seem to per-
mit a firm conclusion, but they point to the possibility of
addressing the phenomena from the standpoint of the
solar weather context. In this way forecasting the com-
plex interplay that often leads to intense disruption on the
Earth could be ultimately possible.
Solar Semi-diameter (arcsec)
Modified Julian Date
Magnetic storms are mainly caused by phenomena in
the Sun that affect the Earth’s atmosphere. In this work
we address a study on the correlation between the solar
semi-diameter and geomagnetic time series. The rest of
the paper is organized as follows, in the next section
(Data series) we expose the experimental details of data
obtaining, and in the subsequent (Data analysis) their
relation to well-established solar and geomagnetic in-
dices. We follow by presenting the results of our analysis
on the relations between the semi-diameter and geomag-
netic series (Solar semi-diameter versus geomagnetic
measurements: Results and Discussion). Finally, in the
Conclusions section we present some final discussion
and possible future approaches.
2. Data Series
Since 1981 our group makes daily solar observations, in
particular, since 1997, aiming to record and study dia-
meter variations [13]. The solar semi-diameter series
treated here was observed with the CCD Astrolabe at our
Rio de Janeiro observatory (Φ = −22˚53.42', Λ = +2 h 52
m 53.5 s, h = 33 m), from March 2nd 1998 to November
27th 2003 (Figure 1). It comprises more than 18,000
observations, with mean internal error of 0.20" and stan-
dard deviation of 0.569" [14].
The observations are made daily, to an average of 20
observations (actually observing days considered), well
distributed throughout the whole year. The gap verified
in the series between September 21st and December 19th
2001 was due to maintenance of the apparatus. The ob-
servations are taken on sessions before and after meri-
dian. As a rule, there is no significant difference between
the measurements from the two sessions, but after April
2000, a bias was verified which was accounted for by a
linear model of the relaxation time of the variable prism.
The heliolatitudes observed cover the whole solar figure
in a semi-annual cycle. The principle of the measure-
ments uses two images of the Sun: one is said direct
while the other follows a path that reflects on a horizon-
tal basin of mercury. To each image, parables are ad-
justed to define the solar limb [15].
The raw data were corrected from effects related to the
Figure 1. Observed solar semi-diameter—1998/2003, at the
Rio de Janeiro station.
observation conditions: the air temperature, its first de-
rivative, the Fried factor and the standard deviation of the
adjusted parable to the directly observed solar edge [16].
The Fried factor was obtained from the observation data
[17].
Further, the instrumental conditions were inspected in
order to detect effects caused by any instability of the
objective prism [18] and from the lacking of leveling of
the astrolabe that could cause errors as function of the
observed azimuth [19]. The standard deviation of the
data fell to 0.567", which showed that all corrections
applied were small and did not introduce any spurious
long-term modulation upon the series. The 2 milli-arcsec
gain on the standard deviation shows that seasonal or
annual effects on the raw measurements are very small,
coherent with the standard refraction theory. The final
series of solar semi-diameter values correlates well to the
series of solar activity parameters in the common period
[20].
The geomagnetic observations consisted in measuring
the H (magnetic northward) component of magnetic field
at our low latitude Vassouras Magnetic Observatory (Φ=
−22˚24.36', Λ= +2h54m45.6s). The H component is es-
sentially the same that the total field component, F, at
that location. Data is recorded at 1 sample/min, providing
more than 44,000 values for each month. The accuracy of
the data is 1 nT and the relative error less than 10−4.
Geomagnetic measurements were performed using an
Intermagnet system (3 component fluxgate and proton
magnetometer) during the whole day.
While the H component geomagnetic measurements
from the Vassouras station are processed at a daily rate,
the Dst index is distributed with a delay of at least two
years. Such delay precludes the verification of much
quicker response searched for the interplay between the
solar diameter variations and the geomagnetic deeps.
Thus, the daily access to both data outcomes from our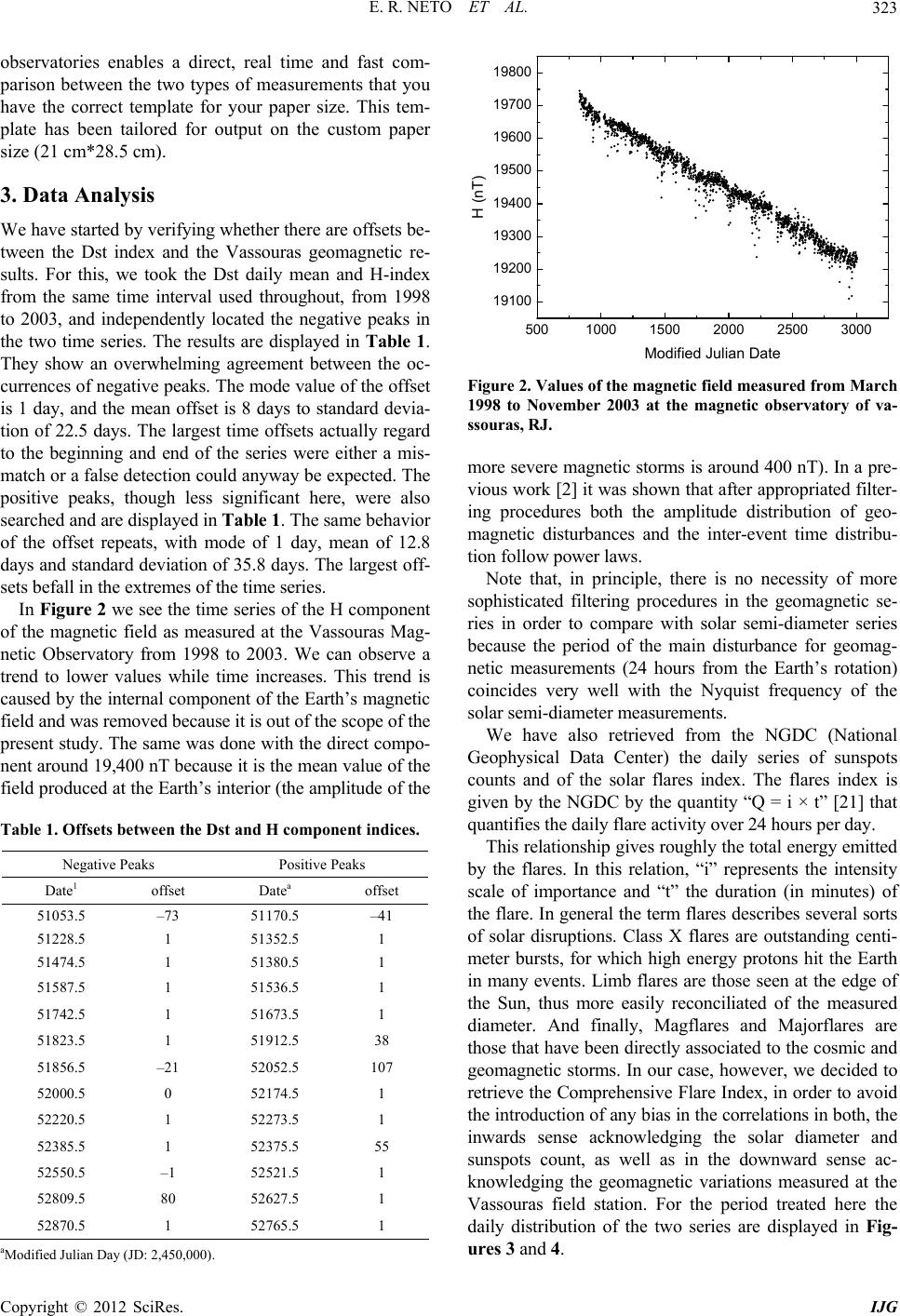

E. R. NETO ET AL. 323
observatories enables a direct, real time and fast com-
parison between the two types of measurements that you
have the correct template for your paper size. This tem-
plate has been tailored for output on the custom paper
size (21 cm*28.5 cm).
5001000 1500 2000 2500 3000
19100
19200
19300
19400
19500
19600
19700
19800
H (nT)
Modified Julian Date
3. Data Analysis
We have started by verifying whether there are offsets be-
tween the Dst index and the Vassouras geomagnetic re-
sults. For this, we took the Dst daily mean and H-index
from the same time interval used throughout, from 1998
to 2003, and independently located the negative peaks in
the two time series. The results are displayed in Table 1.
They show an overwhelming agreement between the oc-
currences of negative peaks. The mode value of the offset
is 1 day, and the mean offset is 8 days to standard devia-
tion of 22.5 days. The largest time offsets actually regard
to the beginning and end of the series were either a mis-
match or a false detection could anyway be expected. The
positive peaks, though less significant here, were also
searched and are displayed in Table 1. The same behavior
of the offset repeats, with mode of 1 day, mean of 12.8
days and standard deviation of 35.8 days. The largest off-
sets befall in the extremes of the time series.
In Figure 2 we see the time series of the H component
of the magnetic field as measured at the Vassouras Mag-
netic Observatory from 1998 to 2003. We can observe a
trend to lower values while time increases. This trend is
caused by the internal component of the Earth’s magnetic
field and was removed because it is out of the scope of the
present study. The same was done with the direct compo-
nent around 19,400 nT because it is the mean value of the
field produced at the Earth’s interior (the amplitude of the
Table 1. Offsets between the Dst and H component indices.
Negative Peaks Positive Peaks
Date1 offset Datea offset
51053.5 –73 51170.5 –41
51228.5 1 51352.5 1
51474.5 1 51380.5 1
51587.5 1 51536.5 1
51742.5 1 51673.5 1
51823.5 1 51912.5 38
51856.5 –21 52052.5 107
52000.5 0 52174.5 1
52220.5 1 52273.5 1
52385.5 1 52375.5 55
52550.5 –1 52521.5 1
52809.5 80 52627.5 1
52870.5 1 52765.5 1
aModified Julian Day (JD: 2,450,000).
Figure 2. Values of the magnetic field measured from March
1998 to November 2003 at the magnetic observatory of va-
ssouras, RJ.
more severe magnetic storms is around 400 nT). In a pre-
vious work [2] it was shown that after appropriated filter-
ing procedures both the amplitude distribution of geo-
magnetic disturbances and the inter-event time distribu-
tion follow power laws.
Note that, in principle, there is no necessity of more
sophisticated filtering procedures in the geomagnetic se-
ries in order to compare with solar semi-diameter series
because the period of the main disturbance for geomag-
netic measurements (24 hours from the Earth’s rotation)
coincides very well with the Nyquist frequency of the
solar semi-diameter measurements.
We have also retrieved from the NGDC (National
Geophysical Data Center) the daily series of sunspots
counts and of the solar flares index. The flares index is
given by the NGDC by the quantity “Q = i × t” [21] that
quantifies the daily flare activity over 24 hours per day.
This relationship gives roughly the total energy emitted
by the flares. In this relation, “i” represents the intensity
scale of importance and “t” the duration (in minutes) of
the flare. In general the term flares describes several sorts
of solar disruptions. Class X flares are outstanding centi-
meter bursts, for which high energy protons hit the Earth
in many events. Limb flares are those seen at the edge of
the Sun, thus more easily reconciliated of the measured
diameter. And finally, Magflares and Majorflares are
those that have been directly associated to the cosmic and
geomagnetic storms. In our case, however, we decided to
retrieve the Comprehensive Flare Index, in order to avoid
the introduction of any bias in the correlations in both, the
inwards sense acknowledging the solar diameter and
sunspots count, as well as in the downward sense ac-
knowledging the geomagnetic variations measured at the
Vassouras field station. For the period treated here the
daily distribution of the two series are displayed in Fig-
ures 3 and 4.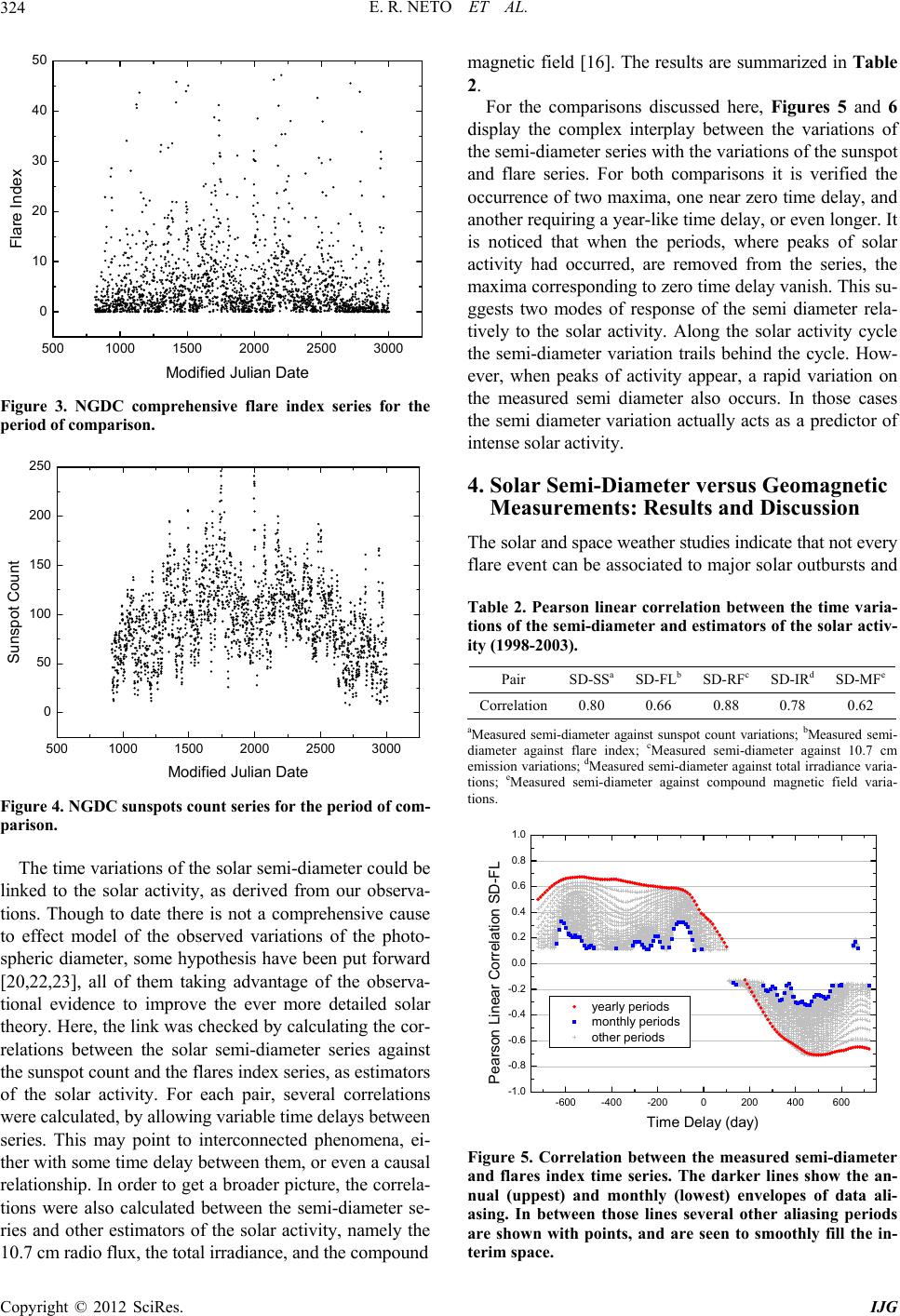

E. R. NETO ET AL. 324
5001000 1500 2000 2500
0
10
20
30
40
50
3000
Flare Index
Modified Julian Date
Figure 3. NGDC comprehensive flare index series for the
period of comparison.
5001000 1500 2000 250
0
50
100
150
200
250
0 3000
Sunspot Count
Modified Julian Date
Figure 4. NGDC sunspots count series for the period of com-
parison.
The time variations of the solar semi-diameter could be
linked to the solar activity, as derived from our observa-
tions. Though to date there is not a comprehensive cause
to effect model of the observed variations of the photo-
spheric diameter, some hypothesis have been put forward
[20,22,23], all of them taking advantage of the observa-
tional evidence to improve the ever more detailed solar
theory. Here, the link was checked by calculating the cor-
relations between the solar semi-diameter series against
the sunspot count and the flares index series, as estimators
of the solar activity. For each pair, several correlations
were calculated, by allowing variable time delays between
series. This may point to interconnected phenomena, ei-
ther with some time delay between them, or even a causal
relationship. In order to get a broader picture, the correla-
tions were also calculated between the semi-diameter se-
ries and other estimators of the solar activity, namely the
10.7 cm radio flux, the total irradiance, and the compound
magnetic field [16]. The results are summarized in Table
2.
For the comparisons discussed here, Figures 5 and 6
display the complex interplay between the variations of
the semi-diameter series with the variations of the sunspot
and flare series. For both comparisons it is verified the
occurrence of two maxima, one near zero time delay, and
another requiring a year-like time delay, or even longer. It
is noticed that when the periods, where peaks of solar
activity had occurred, are removed from the series, the
maxima corresponding to zero time delay vanish. This su-
ggests two modes of response of the semi diameter rela-
tively to the solar activity. Along the solar activity cycle
the semi-diameter variation trails behind the cycle. How-
ever, when peaks of activity appear, a rapid variation on
the measured semi diameter also occurs. In those cases
the semi diameter variation actually acts as a predictor of
intense solar activity.
4. Solar Semi-Diameter versus Geomagnetic
Measurements: Results and Discussion
The solar and space weather studies indicate that not every
flare event can be associated to major solar outbursts and
Table 2. Pearson linear correlation between the time varia-
tions of the semi-diameter and estimators of the solar activ-
ity (1998-2003).
Pair SD-SSaSD-FLb SD-RFc SD-IRdSD-MFe
Correlation0.80 0.66 0.88 0.78 0.62
aMeasured semi-diameter against sunspot count variations; bMeasured semi-
diameter against flare index; cMeasured semi-diameter against 10.7 cm
emission variations; dMeasured semi-diameter against total irradiance varia-
tions; eMeasured semi-diameter against compound magnetic field varia-
tions.
-600-400-2000200 400 600
-1.0
-0.8
-0.6
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
yearly peri od s
monthly per iod s
oth e r per iods
Pearson Linear Correlation SD-F L
Time Delay (day)
Figure 5. Correlation between the measured semi-diameter
and flares index time series. The darker lines show the an-
nual (uppest) and monthly (lowest) envelopes of data ali-
asing. In between those lines several other aliasing periods
are shown with points, and are seen to smoothly fill the in-
terim space.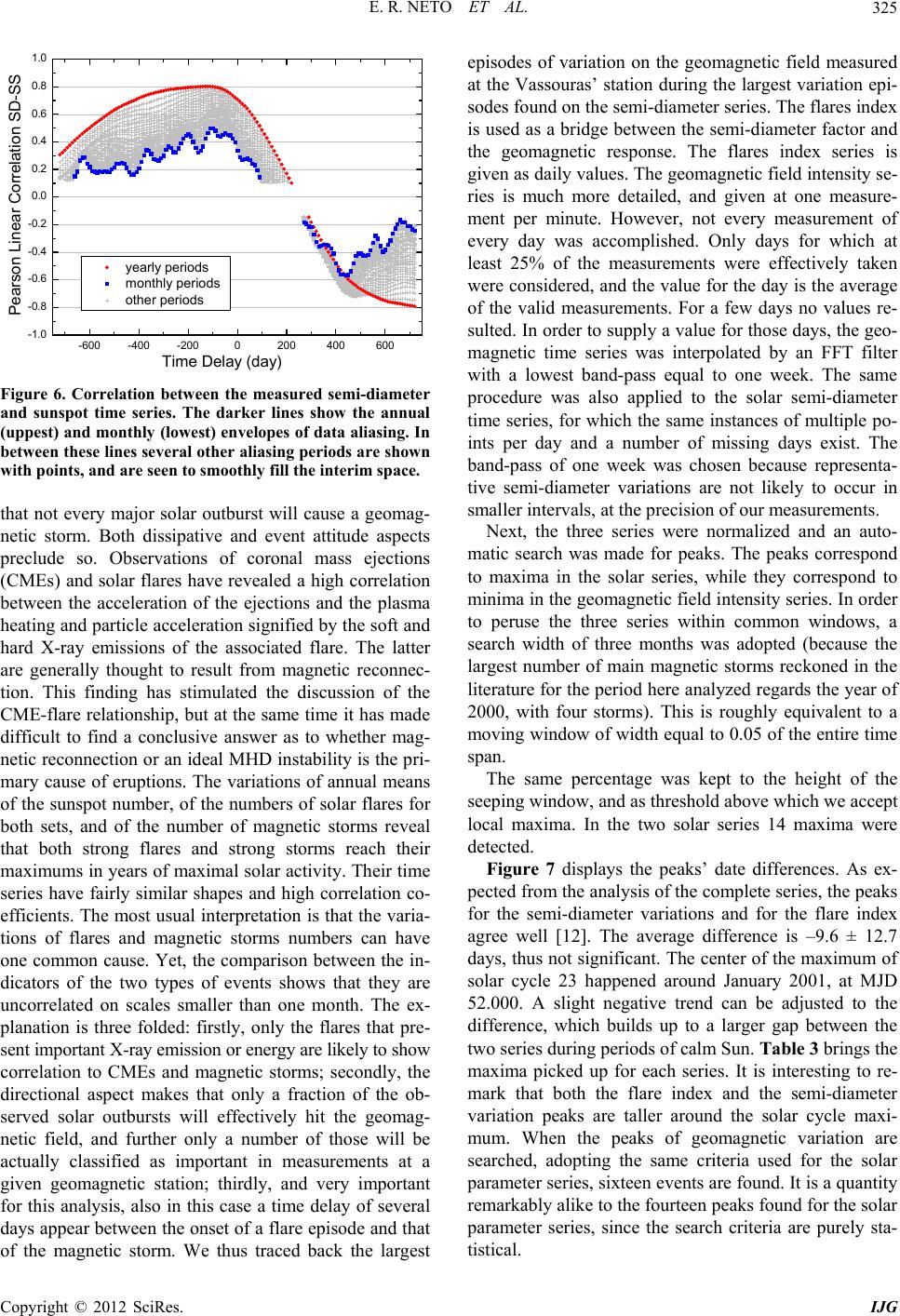

E. R. NETO ET AL. 325
-600 -400 -2000200
-1.0
-0.8
-0.6
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
400 600
Pearson Linear Correlat ion SD-SS
Time Delay (day)
yearly p er io ds
monthly periods
other periods
Figure 6. Correlation between the measured semi-diameter
and sunspot time series. The darker lines show the annual
(uppest) and monthly (lowest) envelopes of data aliasing. In
between these lines several other aliasing periods are shown
with points, and are seen to smoothly fill the interim space.
that not every major solar outburst will cause a geomag-
netic storm. Both dissipative and event attitude aspects
preclude so. Observations of coronal mass ejections
(CMEs) and solar flares have revealed a high correlation
between the acceleration of the ejections and the plasma
heating and particle acceleration signified by the soft and
hard X-ray emissions of the associated flare. The latter
are generally thought to result from magnetic reconnec-
tion. This finding has stimulated the discussion of the
CME-flare relationship, but at the same time it has made
difficult to find a conclusive answer as to whether mag-
netic reconnection or an ideal MHD instability is the pri-
mary cause of eruptions. The variations of annual means
of the sunspot number, of the numbers of solar flares for
both sets, and of the number of magnetic storms reveal
that both strong flares and strong storms reach their
maximums in years of maximal solar activity. Their time
series have fairly similar shapes and high correlation co-
efficients. The most usual interpretation is that the varia-
tions of flares and magnetic storms numbers can have
one common cause. Yet, the comparison between the in-
dicators of the two types of events shows that they are
uncorrelated on scales smaller than one month. The ex-
planation is three folded: firstly, only the flares that pre-
sent important X-ray emission or energy are likely to show
correlation to CMEs and magnetic storms; secondly, the
directional aspect makes that only a fraction of the ob-
served solar outbursts will effectively hit the geomag-
netic field, and further only a number of those will be
actually classified as important in measurements at a
given geomagnetic station; thirdly, and very important
for this analysis, also in this case a time delay of several
days appear between the onset of a flare episode and that
of the magnetic storm. We thus traced back the largest
episodes of variation on the geomagnetic field measured
at the Vassouras’ station during the largest variation epi-
sodes found on the semi-diameter series. The flares index
is used as a bridge between the semi-diameter factor and
the geomagnetic response. The flares index series is
given as daily values. The geomagnetic field intensity se-
ries is much more detailed, and given at one measure-
ment per minute. However, not every measurement of
every day was accomplished. Only days for which at
least 25% of the measurements were effectively taken
were considered, and the value for the day is the average
of the valid measurements. For a few days no values re-
sulted. In order to supply a value for those days, the geo-
magnetic time series was interpolated by an FFT filter
with a lowest band-pass equal to one week. The same
procedure was also applied to the solar semi-diameter
time series, for which the same instances of multiple po-
ints per day and a number of missing days exist. The
band-pass of one week was chosen because representa-
tive semi-diameter variations are not likely to occur in
smaller intervals, at the precision of our measurements.
Next, the three series were normalized and an auto-
matic search was made for peaks. The peaks correspond
to maxima in the solar series, while they correspond to
minima in the geomagnetic field intensity series. In order
to peruse the three series within common windows, a
search width of three months was adopted (because the
largest number of main magnetic storms reckoned in the
literature for the period here analyzed regards the year of
2000, with four storms). This is roughly equivalent to a
moving window of width equal to 0.05 of the entire time
span.
The same percentage was kept to the height of the
seeping window, and as threshold above which we accept
local maxima. In the two solar series 14 maxima were
detected.
Figure 7 displays the peaks’ date differences. As ex-
pected from the analysis of the complete series, the peaks
for the semi-diameter variations and for the flare index
agree well [12]. The average difference is –9.6 ± 12.7
days, thus not significant. The center of the maximum of
solar cycle 23 happened around January 2001, at MJD
52.000. A slight negative trend can be adjusted to the
difference, which builds up to a larger gap between the
two series during periods of calm Sun. Table 3 brings the
maxima picked up for each series. It is interesting to re-
mark that both the flare index and the semi-diameter
variation peaks are taller around the solar cycle maxi-
mum. When the peaks of geomagnetic variation are
searched, adopting the same criteria used for the solar
parameter series, sixteen events are found. It is a quantity
remarkably alike to the fourteen peaks found for the solar
parameter series, since the search criteria are purely sta-
tistical.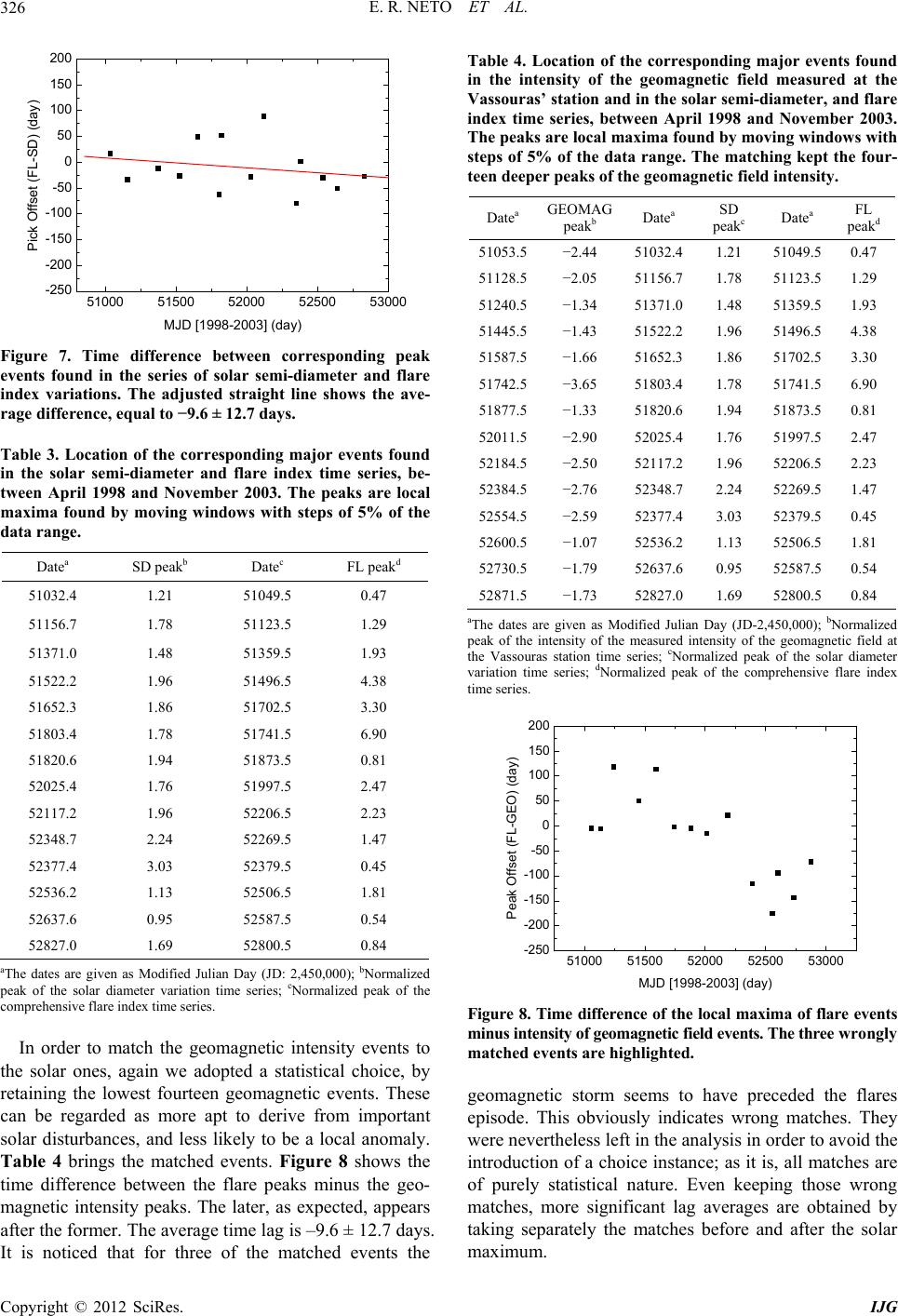

E. R. NETO ET AL. 326
51000 51500 52000 5
-250
-200
-150
-100
-50
0
50
100
150
200
2500 53000
Pick Offset (FL-SD) (day)
MJD [1998-2003] (day)
Figure 7. Time difference between corresponding peak
events found in the series of solar semi-diameter and flare
index variations. The adjusted straight line shows the ave-
rage difference, equal to −9.6 ± 12.7 days.
Table 3. Location of the corresponding major events found
in the solar semi-diameter and flare index time series, be-
tween April 1998 and November 2003. The peaks are local
maxima found by moving windows with steps of 5% of the
data range.
Datea SD peakb Datec FL peakd
51032.4 1.21 51049.5 0.47
51156.7 1.78 51123.5 1.29
51371.0 1.48 51359.5 1.93
51522.2 1.96 51496.5 4.38
51652.3 1.86 51702.5 3.30
51803.4 1.78 51741.5 6.90
51820.6 1.94 51873.5 0.81
52025.4 1.76 51997.5 2.47
52117.2 1.96 52206.5 2.23
52348.7 2.24 52269.5 1.47
52377.4 3.03 52379.5 0.45
52536.2 1.13 52506.5 1.81
52637.6 0.95 52587.5 0.54
52827.0 1.69 52800.5 0.84
aThe dates are given as Modified Julian Day (JD: 2,450,000); bNormalized
peak of the solar diameter variation time series; cNormalized peak of the
comprehensive flare index time series.
In order to match the geomagnetic intensity events to
the solar ones, again we adopted a statistical choice, by
retaining the lowest fourteen geomagnetic events. These
can be regarded as more apt to derive from important
solar disturbances, and less likely to be a local anomaly.
Table 4 brings the matched events. Figure 8 shows the
time difference between the flare peaks minus the geo-
magnetic intensity peaks. The later, as expected, appears
after the former. The average time lag is –9.6 ± 12.7 days.
It is noticed that for three of the matched events the
Table 4. Location of the corresponding major events found
in the intensity of the geomagnetic field measured at the
Vassouras’ station and in the solar semi-diameter, and flare
index time series, between April 1998 and November 2003.
The peaks are local maxima found by moving windows with
steps of 5% of the data range. The matching kept the four-
teen deeper peaks of the geomagnetic field intensity.
Datea GEOMAG
peakb Datea SD peakc Datea FL peakd
51053.5 −2.44 51032.4 1.21 51049.50.47
51128.5 −2.05 51156.7 1.78 51123.51.29
51240.5 −1.34 51371.0 1.48 51359.51.93
51445.5 −1.43 51522.2 1.96 51496.54.38
51587.5 −1.66 51652.3 1.86 51702.53.30
51742.5 −3.65 51803.4 1.78 51741.56.90
51877.5 −1.33 51820.6 1.94 51873.50.81
52011.5 −2.90 52025.4 1.76 51997.52.47
52184.5 −2.50 52117.2 1.96 52206.52.23
52384.5 −2.76 52348.7 2.24 52269.51.47
52554.5 −2.59 52377.4 3.03 52379.50.45
52600.5 −1.07 52536.2 1.13 52506.51.81
52730.5 −1.79 52637.6 0.95 52587.50.54
52871.5 −1.73 52827.0 1.69 52800.50.84
aThe dates are given as Modified Julian Day (JD-2,450,000); bNormalized
peak of the intensity of the measured intensity of the geomagnetic field at
the Vassouras station time series; cNormalized peak of the solar diameter
variation time series; dNormalized peak of the comprehensive flare index
time series.
51000 51500 52000 52500 53000
-250
-200
-150
-100
-50
0
50
100
150
200
Peak Offset (FL-GEO) (day)
MJD [1998-2003] (day)
Figure 8. Time difference of the local maxima of flare events
minus intensity of geomagnetic field events. The three wrongly
matched events are highlighted.
geomagnetic storm seems to have preceded the flares
episode. This obviously indicates wrong matches. They
were nevertheless left in the analysis in order to avoid the
introduction of a choice instance; as it is, all matches are
of purely statistical nature. Even keeping those wrong
matches, more significant lag averages are obtained by
taking separately the matches before and after the solar
maximum.

E. R. NETO ET AL. 327
Before the maximum the average is 23.8 ± 18.6 days
(the wrong matches making the average statistically null),
while after the solar maximum the average is –61.0 ± 9.9
days. This can be interpreted as if as long the solar cycle
subdues, more and more solar flares become required to
build up a magnetic storm. On the other hand, the depen-
dence verified between the peaks of the semi-diameter
and flares variations, leads to a somehow relevant inter-
play between the peaks of the solar diameter variations
and the peaks of the geomagnetic field intensity, as
shown in Figure 9. During periods of calm Sun the semi-
diameter variations precede the matched geomagnetic
storms by 60 days, while (the above discussed wrong
matches, put aside) there is a little time lag when the Sun
is most active. If further data confirm such behavior, the
measurements of the semi-diameter can provide an easy
access technique to forecast potentially hazardous events
later translated as peaks of variation on the intensity of
the geomagnetic field.
5. Conclusions
The combination of associated measurements of the
geomagnetic field and the solar diameter, by two of our
ground stations, makes evident a match between peaks
found in both time series during the interval from March
1998 to November 2003. The solar diameter series was
confronted with five estimators of the solar activity, and
found in good correlation to them, when time delays are
allowed. The geomagnetic time series was compared to
the Dst index time series, and a very good agreement was
found too. For the intercomparison between the series, in
order to remediate missing points, a FFT routine was em-
ployed, with lowest band-pass equal to one week. Peaks
in the series were located by moving windows of dimen-
sion equal to 5% of the respective breadths. In particular,
regarding the length of those series, this is commensura-
51000 51500 52000 52
-250
-200
-150
-100
-50
0
50
100
150
200
500 53000
Peak Offset (SD-GS) (day)
DJM [1998-2003] (day)
Figure 9. Time difference of the local maxima of semi-dia-
meter variations minus intensity of geomagnetic field events.
The points at which those events occur, on average, with a
difference of about 60 days are highlighted.
ble to the sampling of geomagnetic storms actually veri-
fied in the interval. During the period corresponding to
the maximum of the solar activity cycle, there is no sta-
tistical significant offset between peaks in the solar di-
ameter series and negative peaks in the series of the H
component of the geomagnetic field. On the other hand,
as the Sun becomes calm, the solar diameter peaks start
to precede the geomagnetic dips. For the calm Sun peri-
ods, the average is found as –61.0 ± 9.9 days. The solar
flares index time series intermediates the relationship. On
the long run, a year-like time offset is demanded to reach
a large correlation coefficient between the flares index
and solar diameter time series. On the other hand, the
largest peaks of both series coincide. This is suggestive
of a scenario in which off the maximum of the solar cy-
cle a larger number, or lengthier events, are required to
supply the energy that will ultimately build up to a mas-
sive coronal event. Therefore the middle point of the en-
ergy supplier and of the coronal events will be progre-
ssively displaced. If new data confirm this behavior,
measurements of the semi-diameter can provide a practi-
cal, easy access, way to predict potentially dangerous
events associated to important variations in the intensity
of the geomagnetic field.
6. Acknowledgements
The authors acknowledge partial financial support from
the Brazilian Science Funding Agencies FAPERJ, CNPq,
CAPES and FINEP.
REFERENCES
[1] D. Sornette, “Critical Phenomena in Natural Sciences,”
Springer, Berlin, 2004.
[2] A. R. R. Papa, L. M. Barreto and N. A. B. Seixas, “Statis-
tical Study of Magnetic Disturbances at the Earth’s Sur-
face,” Journal of Atmospheric and Solar-Terrestrial Phy-
sics, Vol. 68, No. 8, 2006, pp. 930-936.
doi:10.1016/j.jastp.2006.01.004
[3] A. R. R. Papa and L. P. Sosman, “Statistical Properties of
Geomagnetic Measurements as a Potential Forecast Tool
for Strong Perturbations,” Journal of Atmospheric and
Solar-Terrestrial Physics, Vol. 70, No. 7, 2008, pp. 1102-
1109. doi:10.1016/j.jastp.2008.01.010
[4] R. T. Merrill, M. W. McElhinny and P. L. McFadden,
“The Magnetic Field of the Earth: Paleomagnetism, the
Core, and the Deep Mantle,” Academic Press, San Diego,
1998.
[5] V. H. A. Dias, A. R. R. Papa and J. O. Franco, “Simu-
lation of Geomagnetic Reversals through Magnetic Criti-
cal Models,” Brazilian Journal of Physics, Vol. 38, No. 1,
2008, pp. 12-19. doi:10.1590/S0103-97332008000100004
[6] S. Dimitrova, “Different Geomagnetic Indices as an Indi-
cator for Geo-Effective Solar Storms and Human Physio-
logical State,” Journal of Atmospheric and Solar Terres-
trial Physics, Vol. 70, No. 2-4, 2008, pp. 420-427.

E. R. NETO ET AL. 328
doi:10.1016/j.jastp.2007.08.050
[7] I. Stoilova and S. Dimitrova, “Geophysical Variables and
Human Health and Behavior,” Journal of Atmospheric
and Solar Terrestrial Physics, Vol. 70, No. 2-4, 2008, pp.
428-435. doi:10.1016/j.jastp.2007.08.053
[8] H. Gleisner, O. Rasmussen and J. Watermann, “Large-
Magnitude Geomagnetic Disturbances in the North Sea
Region: Statistics, Causes and Forecasting,” Advances in
Space Research, Vol. 37, No. 6, 2006, pp. 1169-1174.
doi:10.1016/j.asr.2005.04.082
[9] S. A. Pulinets and K. A. Boyarchuk, “COMPASS-2 and
VULKAN Satellite System for the Short-Term Earth-
quake Warning,” American Geophysical Union, Fall Mee-
ting, Abstract T51B-0452, 2004.
[10] L. Damé, D. Cugnet, M. Herse, D. Crommelynck, S.
Dewitte, A. Joukoff, I. Ruedi, W. Schmutz, C. Wehrli, C.
Delmas, F. Laclare and J. P. Rozelot, “PICARD: Solar
Diameter, Irradiance and Climate,” Proceedings of the 1st
Solar and Space Weather Euroconference, Tenerife, 25-
29 September 2000, pp. 223-223.
[11] W. M. Neupert, B. J. Thompson, J. B. Gurman and S. P.
Plunkett, “Eruption and Acceleration of Flare-Associated
Coronal Mass Ejection Loops in the Low Corona,” Jour-
nal of Geophysical Research, Vol. 106, No. A11, 2001,
pp. 25215-25226. doi:10.1029/2000JA004012
[12] J. Zhang and J. Wang, “Are Homologous Flare-Coronal
Mass Ejection Events Triggered by Moving Magnetic
Features?” Astronomical Journal, Vol. 566, No. 2, 2002,
pp. 117-120.
[13] E. G. Jilinski, S. P. Puliaev, J. L. Penna, A. H. Andrei, V.
Sinceac, F. Chollet and C. Delmas, “Solar Diameter Ob-
servations with the Astrolabe at Observatório Nacional-
Rio de Janeiro,” Astronomy & Astrophysics, Vol. 130,
1998, pp. 317-321.
[14] A. H. Andrei, J. L. Penna, E. Reis Neto, E. G. Jilinki, S. C.
Boscardin, C. Delmas, F. Morand and F. Laclare, “Solar
Diameter Observations on the Maximum of Cycle 23,”
Journées 2002—Systèmes de Référence Spatio-Temporels,
Astrometry from Ground and from Space, 2003, pp.
185-188.
[15] V. Sinceac, “Analyse et Exploitation des Observations du
Passage du Soleil Partir de l’Astrolabe Danjon quip d’une
camra CCD,” Ph.D. Thesis, Paris Observatory, Paris,
1998.
[16] S. C. Boscardin, A. H. Andrei, J. L. Penna, E. Reis Neto
and V. A. d’Ávila, “Solar Semi-Diameter Results from
the Rio de Janeiro State—1998/2003,” 2011.
[17] L. Lakhal, A. Irbah, M. Bouzaria, J. Borgnino, F. Laclare
and C. Delmas, “Error Due to Atmospheric Turbulence
Effects on Solar Diameter Measurements Performed with
an Astrolabe,” Astronomy & Astrophysics, Vol. 138, 1999,
pp. 155-162.
[18] E. Reis Neto, “Observações Solares: Estudo das Varia-
ções do Diâmetro e Suas Correlações,” M.Sc. Dissertation,
Observatório Nacional, Rio de Janeiro, 2002.
[19] S. C. Boscardin, “Análise de Observações do Diâmetro
no Contexto da Atividade Solar,” M.Sc. Dissertation,
Observatório do Valongo/UFRJ, Rio de Janeiro, 2006.
[20] A. H. Andrei, S. C. Boscardin, E. Reis Neto, J. L. Penna
and V. A. d’Ávila, “Solar and Stellar Activity Cycles,”
26th Meeting of the IAU, JD08, 2006, pp. 36-36.
[21] J. Kleczek, “Ionospheric Disturbances and Flares in the
11 Years Cycle,” Bulletin of the Central Astronomical In-
stitute of Czechoslovaquia, Vol. 3, 1952, pp. 52-63.
[22] S. Sofia, S. Basu, P. Demarque, L. Li and G. Thuillier,
“The Nonhomologous Nature of Solar Diameter Varia-
tions,” Astrophysical Journal, Vol. 632, No. 2, 2005, pp.
L147-L150. doi:10.1086/498068
[23] C. Damiani-Badache, J. P. Rozelot, K. Coughlin and N.
Kilifarska, “Influence of the UTLS Region on the Astro-
labes Solar Signal Measurements,” Monthly Notice Royal
Astronomical Society, Vol. 380, No. 2, 2007, pp. 609-614.
doi:10.1111/j.1365-2966.2007.12079.x