Journal of Modern Physics
Vol.07 No.15(2016), Article ID:72434,12 pages
10.4236/jmp.2016.715192
Spring Theory as an Approach to the Unification of Fields
Ling Man Tsang
Fisica Laboratorio, TIS, Macau University of Science and Technology, Macau, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 16, 2016; Accepted: November 27, 2016; Published: November 30, 2016
ABSTRACT
The cosmological constant is necessary to be retained in Einstein’s field equations with value depending on the mass of the source. An overview of the spring theory in astrophysics and cosmology is included in this paper. In short range force, the two interacting particles are point-like vertices connected by a bosonic spring. We also suspect that electron may contain negative sterile neutrino. The self energy of a point charge is not infinite so that renormalisation is not necessary.
Keywords:
Cosmological Constant, Dark Matter, Classical Electrostatics, Short Range Interaction

1. Introduction
Astrophysical standard model has confirmed to accept the cosmological constant in relating to dark energy―undetectable particles same as dark matter. The matter distribution inside the universe is roughly dark fluid 95 percent and normal matter 5 percent. Different notions such as dark energy, dark matter, aether, pure space and others are of the same entity. They are different manifestations of the same dark fluid aether, just like the extension and compression of a spring [1] [2] . The famous Michelson-Morley experiments provide no proofs to decline the existence of aether; moreover, the basic assumptions of these experiments are wrong [3] [4] . The theory in this paper is in fact a three dimensional treatment of the de-Sitter Schwarzschild solution. Simply speaking, a spring term is added into Newton’s gravitation. With such a model, we can derive easily the Hubble’s law, explain the missing mass in the rotation curve of galaxies, and depict the short range interaction in which the two point-like vertices are connected by a bosonic spring. Spring theory is based on two resources; the theoretical Yang’s pure space and the results of the Pound-Rebka experiments on the photonic frequency changes along a vertical path.
1.1. Yang’s Pure Space [5]
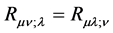 (1)
(1)
Or, after contraction of  and
and 
 (2)
(2)
Properties of these equations had been studied by various authors [6] [7] [8] . Pavelle [6] pointed out that Yang’s pure space is non-physical unless the cosmological constant remains in Einstein’s field equations which was later verified by Mielke [8] . We begin from the second Bianchi Identity
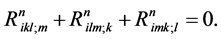 (3)
(3)
For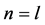 , we have
, we have
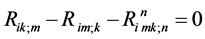 (4)
(4)
Operating 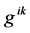 on above, we have
on above, we have
 (5)
(5)
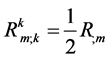 (6)
(6)
Comparing with Equation (2), R is a constant. Now the Einstein’s field equations with the cosmological constant can be written as
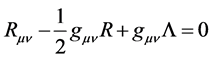 (7)
(7)
We obtain in the 4-dimensional case
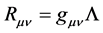 (8)
(8)
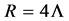 (9)
(9)
indicating that Einstein’s case is a special solution of Yang’s pure space where the covariant derivative of the Ricci tensor in Einstein’s case is zero but not in Yang’s case.
Hence, the cosmological constant needs to be retained but to be re-named as spring constant since it behaves like a harmonic oscillator as we can see later. In a 3-dimensional space, a spring term is added into Newton’s law of gravity:
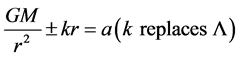 (10)
(10)
where k is the spring constant of the source while 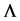 is assigned as the spring constant of the universe which also known as the cosmological constant. Throughout this paper, only 3-dimensional springs are to be considered.
is assigned as the spring constant of the universe which also known as the cosmological constant. Throughout this paper, only 3-dimensional springs are to be considered.
1.2. The Pound-Rebka Experiments
These famous experiments can be found in many textbooks (see Gravitation by Misner/Thorne/Wheeler). The main purpose was to measure the frequency changes of photons under the earth’s gravity. The Jefferson Physical Laboratory at Harvard used a 57Fe source placed at a height of 22.6 m above the detector.
Data were obtained when the gamma ray dropped onto the detector:
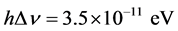 (11)
(11)
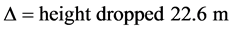 (12)
(12)
 (13)
(13)

which is only true at Harvard, or likewise, the state of Massachusetts. In 1965 Pound and Snider refined the apparatus so that the energy shifts on the upward and downward path gave the measured difference of

Since the first term of Equation (15) is known, the second term will immediately yield the deceleration of
the earth’s rotation
the earth’s radius
the earth’s mass 

being the latitude of Massachusetts where Pound and Rebka performed their experiments at Harvard. Upon substituting the acceleration 



Thus, the spring constant of the earth 
2. An Overview of the Spring Theory in Astronomy and Astrophysics
2.1. Spring of the Earth
From Equation (10), there exists a point or a spherical shell at a distance of 




The last equation shows that the spring breaks at the distance of 32,000 km away from us. Equation (10) gives a clear picture of the fifth force different from the Yukawa type [9] - [15] . However, we have pointed out that the Yukawa type of fifth force is non-logical at 
2.2. The Spring of the Moon
The almost vacuum lunar surface provides a frictionless condition for a free falling test to verify the existence of the fifth force as well as to obtain the spring of the moon. The total time travelled by a free falling object through a height H can simply be found as

where 
If fifth force does exist, the total time T must take longer than the classical one without the spring term [16] .
2.3. The Spring of the Sun
The Binet Equation (53) yields the solution [17]

where D is a constant. Setting the cosine part to zero, the spring of the sun is
Table 1. Orbital details of the inner planets.
Table 2. Comparison of different k (/sec2) values.

Table 1 can be found in many astronomy textbooks. From Table 2, we can see that the average value of k is higher than those from various authors.
There are two main reasons of difficulty in determining the value of the sun’s k:
・ the value of the two terms inside the bracket of Equation (27) is so close to each other.
・ planetary interaction has not been taking into account.
However, the spring term of Equation (26) contributes insignificantly in the perihelion shift of planetary motion as well as the bending of light while grazing the sun.
2.4. The Cosmological Constant of the Universe
There are 3 main parameters in any cosmological model, namely the cosmological constant, the Hubble constant and the matter density [22] . In such a large scale structure, 3 dimensional space is sufficient to depict the universe instead of general relativity [23] , Milne [24] and McCrea [25] used Newtonian mechanics to derive the cosmological equations while Harrison used the first law of thermodynamics and equations of hydrodynamics [26] .
In the beginning, all matters were compressed into a high density lump of universe followed by a release in such a way that all matters were sprung out by the spring(s) as governed by the equation

which is the same approach as Konuschko [27] except the cosmological term was not considered in his paper. Now,




Equation (28) can be reduced to, upon integration:

which is just the Hubble’s law having the Hubble constant 



or 
2.5. The Missing Mass in the Rotation Curve of Galaxies
It is already known that the cosmological constant is the answer of dark matter [31] , or more precisely, variable cosmological constant [32] . This is explicitly referring to the spring constant of the galaxy, but awaiting to be spelt out. Again, in such a large scale of structure, only approximate estimation can be achieved with the following assumptions:
・ aberrations in the observed velocity and distance are unavoidable [33] [34] .
・ the radius R of the cluster and the velocity can be estimated from the rotation curve.
・ •
In the quantum version of the virial theorem, the average value of the operator T in energy eigenstates in one dimension is given by

where T is kinetic energy and V is potential energy. Since the angular velocity of the galaxies is very small:
We have studied the rotation curves of galaxies in Figure 1 and Figure 2 with the help of the virial theorem.

Nearly all these rotation curves yield the same (for detail see [17] )


It is clear that each mass has only one unique spring constant assigned to it. Strictly speaking. a flat curve means that the mass is still decreasing depending on 









3. The Electric Field
The electric field energy density W surrounding a charge q is proportional to the square of the field intensity E
Figure 1. NGC 4594, 2590, 1620 and 7664 [35] .
Figure 2. Circular speed versus radius of our galaxy: curve D for le vancouleurs and Pence. B for Bathcall and Soneira [36] .

Since a charge is always accompanied by its electromagnetic mass


which seems to be reasonable to say the energy density of the source is proportional to the energy density of its surrounding field. Upon integration

A and B are constants. Integrating over the whole space, and set A = charge q, the total energy

which is just the Gauss Law except the right hand side of of Equation (42) is not 


The potential can be written as


where A and B need to be determined in short range since coupling is involved. Obviously, for




and

Among the 4 pairs solution after solving the above, the most logical pair is



Instead, through the electron-positron scattering, the upper limit of 

resulting to a value less than 1 eV: too small to affect the fine structure of hydrogen spectrum.
4. The Gravitational Field
As both the Coulomb and Newton’s inverse square law are analogous to one another, the gravitational field from Equation (42) becomes

where

Including the spring term, the new Binet equation can be written as

To solve for the above Equation (53), we followed the same procedures as in [42] and [43] to get Equation (26). Comparing the tests with general relativity, the spring term contributes insignificantly in the bending of light while grazing the sun whereas the perihelion shift of a planet gives

5. Spring in the Short Range Interaction
Figure 3 shows the quarkonium potential energy which can be governed by the following 3 equations:
a) Cornell potential

where

Figure 3. Quarkonium potential from fitting the energy levels [44] .
b) Natural log potential

where

c) Spring theory (Equation (45) + spring term)

where a and b can be estimated roughly from the graph. However, the constant C is in fact the energy of the spring or rather say, the energy of the confined quarkonia. It follows that

There are many combinations of a and b in Equation (57). For instance, for charmonium, 






6. Discussions
Revisiting the equations from (40) to (45), we come to something interesting:
・ total field energy of a charge particle with radius R

・ total self energy of a charge with radius R

For R = 0, none of the above tends to infinity. In a book written by Sapogin [47] , it was mentioned that the classical theory of electromagnetism was fundamentally wrong. The electric field at the centre is zero because E is a vector. Feyman pointed out that Coulomb’s inverse square law fails at very short distance (see Feyman Lectures on Physics volume 2 chapter 5.8). Hence, renormalisation is not necessary. Perhaps short range Maxwell’s equations can be furtherly elaborated towards a new branch of electromagnetism [48] .
Cite this paper
Tsang, L.M. (2016) Spring Theory as an Approach to the Unification of Fields. Journal of Modern Physics, 7, 2219-2230. http://dx.doi.org/10.4236/jmp.2016.715192
References
- 1. Zhao, H. (2007) The Astrophysical Journal Letters, 67, L1-L4.
https://doi.org/10.1086/524731 - 2. Tsang, L.M. (2012) Applied Physics Research, 4, 229-232.
- 3. Sandhu, G.S. (2016) Applied Physics Research, 8, 45-57.
https://doi.org/10.5539/apr.v8n3p45 - 4. Apsden, H. (1969) Physics without Einstein. Sabberton Publication, University of Southampton, Southampton, 36, 59.
- 5. Yang, C.N. (1974) Physical Review Letters, 33, 445-447.
https://doi.org/10.1103/PhysRevLett.33.445 - 6. Pavelle, R. (1974) Physical Review Letters, 33, 1461-1463.
https://doi.org/10.1103/PhysRevLett.33.1461 - 7. Guilfoyle, B.S. and Nohan, B.C. (1998) General Relativity and Gravitation, 30, 473-495.
https://doi.org/10.1023/A:1018815027071 - 8. Mielke, E.W. and Maggiolo, A.A.R. (2005) General Relativity and Gravitation, 37, 997-1007.
https://doi.org/10.1007/s10714-005-0083-2 - 9. Burgess, C.P. and Cloutier, J. (1988) Physical Review D, 3, 2944-2964.
https://doi.org/10.1103/PhysRevD.38.2944 - 10. Fischbach, E. and Talnadge, C. (1992) Nature, 356, 207-215.
- 11. Sereno, M. and Jetzer, P. (2006) MNRAS, 371, 626-632.
https://doi.org/10.1111/j.1365-2966.2006.10670.x - 12. Iorio, L. (2007) Planetary and Space Science, 55, 1290-1298.
https://doi.org/10.1016/j.pss.2007.04.001 - 13. Haranus, I. and Ragos, O. (2011) Astrophysics and Space Science, 331, 115-119.
https://doi.org/10.1007/s10509-010-0440-9 - 14. Kolosnisyn, N.I. and Melnikov, V.N. (2004) General Relativity and Gravitation, 36, 1619-1624.
https://doi.org/10.1023/B:GERG.0000032154.73097.5b - 15. Lucchesi, D.M. (2003) Physics Letters A, 318, 234-240.
https://doi.org/10.1016/j.physleta.2003.07.015 - 16. Tsang, L.M. (2012) New Astronomy, 17, 18-21.
https://doi.org/10.1016/j.newast.2011.05.004 - 17. Tsang, L.M. (2013) Journal of Modern Physics, 9, 1205-1212.
https://doi.org/10.4236/jmp.2013.49164 - 18. Jetzer, P. and Sereno, M. (2006) Physical Review D, 73, Article ID: 044015.
https://doi.org/10.1103/PhysRevD.73.044015 - 19. Cardona, J.F. and Tejeiro, J.M. (1998) The Astronomical Journal, 493, 52-53.
https://doi.org/10.1086/305125 - 20. Iorio, L. (2006) International Journal of Modern Physics D, 15, 473-476.
https://doi.org/10.1142/S021827180600819X - 21. Adkins, G.S. and Mc Donnell, J. (2007) Physical Review D, 75, Article ID: 082001.
https://doi.org/10.1103/PhysRevD.75.082001 - 22. Bertin, G. (2014) Dynamics of Galaxies. 2nd Edition, Chapter 4, Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9780511731990 - 23. Perlmutter, S. and Schmidt, B.R. (2003) Measuring Cosmology with Supernovae. In: Weiler, K., Ed., Supernovae & Gamma Ray Bursts, Springer, Berlin, 195-217.
https://doi.org/10.1007/3-540-45863-8_11 - 24. Milne, E.A. (1934) Quarterly Journal of Mathematics, 5, 64-72.
https://doi.org/10.1093/qmath/os-5.1.64 - 25. McCrea, W.H. and Milne, E.A. (1934) Quarterly Journal of Mathematics, 5, 73-80.
https://doi.org/10.1093/qmath/os-5.1.73 - 26. Harrison, E.R. (1965) Annals of Physics, 37, 437-446.
https://doi.org/10.1016/0003-4916(65)90249-6 - 27. Konuschko, V. (2012) Journal of Modern Physics, 3, 1819-1829.
https://doi.org/10.4236/jmp.2012.311227 - 28. Freedman, W.L. and Madore, B.E. (2010) Annual Review of Astronomy and Astrophysics, 48, 673-710.
https://doi.org/10.1146/annurev-astro-082708-101829 - 29. Davis, T.M. and Lineweaver, C.H. (2004) Astronomical Society of Australia, 21, 97-109.
https://doi.org/10.1071/AS03040 - 30. Kiang, T. (2003) Chinese Journal of Astronomy and Astrophysics, 27, 247-251.
- 31. Peebles, P.J.E. and Ratra, B. (2003) Reviews of Modern Physics, 75, 559-606.
https://doi.org/10.1103/RevModPhys.75.559 - 32. Mishra, R.K. and Singh, A. (2011) International Journal of Research and Review in Applied Sciences, 8, 1-7.
- 33. Kraft, R.P. (1965) Astrophysical Journal, 142, 681-702.
https://doi.org/10.1086/148330 - 34. Van Leeuwen, F. and Le Poole, R.S. (2002) Astrophysics ASP Conference Series, 265, 41-50.
- 35. Bless, R.C. (1996) Discovering the Cosmos. University Science Book, 461.
- 36. Bnney, J. and Tremaine, S. (1987) Galactic Dynamics. Princeton University Press, Princeton, 87.
- 37. Gessner, E. (1992) Astrophysics and Space Science, 194, 197-205.
https://doi.org/10.1007/BF00643990 - 38. Aryal, B., et al. (2012) Bulletin of the Astronomical Society of India.
- 39. Weisskopf, V.F. (1949) Reviews of Modern Physics, 21, 305-315.
https://doi.org/10.1103/RevModPhys.21.305 - 40. Bonnor, W.B. and Cooperstock, F.I. (1989) Physics Letters A, 139, 442-447.
https://doi.org/10.1016/0375-9601(89)90941-9 - 41. Blinder, S.M. (2002) International Journal of Quantum Chemistry, 90, 144-147.
https://doi.org/10.1002/qua.1806 - 42. Adler, R., Bazin, N. and Schiffer, M. (1975) Introduction to General Relativity. 2nd Edition, Mcgraw Hill, New York, 485.
- 43. Tsang, L.M. (2010) Canadian Journal of Pure and Applied Sciences, 4, 1073-1079.
- 44. Martin, B.R. and Shaw, G. (2008) Particle Physics. 3rd Edition, John Wiley and Sons, Hoboken, 172-176.
- 45. Chung, H.S., et al. (2008) Journal of the Korean Physical Society, 52, 1151-1154.
- 46. Bhaduri, R.K., Cohler, L.E. and Nogami, Y. (1981) Il Nuovo Cimento A, 65, 376-390.
https://doi.org/10.1007/BF02827441 - 47. Sapoqin, L., Ryabov, Y. and Boichenko, V. (2005), Unitary Quantum Theory. Archer Enterprises, New York, 9.
- 48. Ivanov, D. and Kolikov, K. (2013) Natural Science, 5, 508-513.
https://doi.org/10.4236/ns.2013.54064






