Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60707,12 pages
10.4236/jmp.2015.613196
Role of Entanglement in Quantum Neural Networks (QNN)
Manu P. Singh1, B. S. Rajput2*
1Department of Computer Science, Institute of Engineering & Technology, Khandari Campus, DR. BR Ambedkar University, Agra (U. P.), India
2 I-11, Gamma-II, Greater Noida (U.P.), India
Email: manu_p_singh@hotmail.com, *bsrajp@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 July 2015; accepted 25 October 2015; published 29 October 2015
ABSTRACT
Starting with the theoretical basis of quantum computing, entanglement has been explored as one of the key resources required for quantum computation, the functional dependence of the entangle- ment measures on spin correlation functions has been established and the role of entanglement in implementation of QNN has been emphasized. Necessary and sufficient conditions for the general two-qubit state to be maximally entangled state (MES) have been obtained and a new set of MES constituting a very powerful and reliable eigen basis (different from magic bases) of two-qubit systems has been constructed. In terms of the MES constituting this basis, Bell’s States have been generated and all the qubits of two-qubit system have been obtained. Carrying out the correct computation of XOR function in neural network, it has been shown that QNN requires the proper correlation between the input and output qubits and the presence of appropriate entanglement in the system guarantees this correlation.
Keywords:
Entanglement, Maximally Entangled State (MES); Quantum Neural Network (QNN), Eigen Basis, Quantum Associated Memory (Qu AM)

1. Introduction
Richard Feynman examined the role quantum mechanics can play in the development of future computer hardware and demonstrated [1] that time evolution of an arbitrary quantum state was intrinsically more powerful computationally than the evolution of logical classical state. Since then, quantum computing has attracted wide attention and soon become the hot topic of research, especially after Shor’s quantum prime factoring algorithm [2] and Grover’s random data base search algorithm [3] were proposed. Quantum Computer (QC) is quantum information processing. It is a relatively new discipline and not yet completely understood, however, it provides an excellent introduction to many key ideas. Simon [4] demonstrated the power of quantum computation and proved quadratic reduction of the amount of quantum data required if quantum states rather than classical states were transmitted and Vetura and Martinez [5] demonstrated potential of quantum system to exhibit correlations that cannot be accounted classically. There are two main motivations for applying capabilities of quantum computation to neural networks: to compensate the ever decreasing scale in hardware development and to produce computational capability not available in classical neural computation. Zak [6] combined classical and quantum neural networks and developed quantum decision maker and Bshouty and Jackson [7] demonstrated superiority of quantum learning algorithm over classical one in certain situations like Quantum Hopfield Networks and Quantum Associative Memories (Qu. AM). Quantum entanglement [8] is one of the most interesting features of quantum mechanics and it provides promising and wide applications in quantum information processing such as teleportation [9] , dense coding [10] [11] , geometric quantum computation [12] [13] , quantum neural computing [14] -[16] , universal quantum computing network [17] -[19] and quantum cryptography [20] -[22] . Measurement and manipulation of entangled state of many particles system becomes a far reaching consequence of quantum information processing.
The physically allowed degree of entanglement and mixture is a timely issue given that the entangled mixed states could be advantageous for certain quantum information situation [23] . The simplest non-trivial multi-par- ticle system that can be investigated theoretically, as well as experimentally, consists of two qubits which display many of the paradoxical features of quantum mechanics such as superposition and entanglement. Basis of entanglement is the correlation that can exist between qubits. From physical point of view, entanglement is still little understood. What makes it too powerful is the fact that since quantum states exist as superposition, these correlations exist in superposition as well and when superposition is destroyed, the proper correlation is somehow communicated between the qubits. It is this communication that is the crux of entanglement. Entanglement is one of the key resources required for quantum computation and hence the experimental creation and measurement of entangled states is of crucial importance for various physical implementations of quantum computers. The generation of quantum entanglement among spatially separated particles requires non-local interactions through which the quantum correlations are dynamically created [24] , but our present knowledge of quantum entanglement is not at all satisfactory [25] .
Starting with the theoretical basis of quantum computing in the present paper, entanglement has been explored as one of the key resources required for quantum computation, the functional dependence of the entanglement measures on spin correlation functions has been established and the role of entanglement in implementation of QNN has been emphasized. It has been shown that the degree of entanglement for a two-qubit state depends on the extent of fractionalization of its density matrix and that the entanglement is completely a quantum phenomenon without any classical analogue. A reliable measure of entanglement of two-qubit states has also been expressed in terms of concurrence [26] [27] and it has been shown that in a free two-qubit system the states with both combinations of parallel spins (i.e. states with maximum Hamming spread) are definitely maximally entangled states (MES) while among the states with minimum Hamming spread, those with both anti- parallel combinations are MES and those with one combination of parallel spins and other with anti-parallel spins are not entangled at all. Necessary and sufficient conditions for the general two-qubit state to be maximally entangled state have been obtained and the conditions for this state to be non-entangled (i.e. separable) and to be partially entangled respectively, have been derived. Two different sets of maximally entangled two-qubit states have been obtained and it has been shown that the set of Bell states [26] is not the only eigen basis (magic eigen basis) of the space of two-qubit system, another set of MES also constitutes a very powerful and reliable eigen basis of two-qubit systems. This is the new eigen basis, being introduced for the first time, and to differentiate it from the already known Bell’s basis, it has been named as Singh-Rajput basis for its possible use in future in the literature. In terms of the MES constituting this basis, Bell’s States have been generated and all the qubits of two-qubit system have been obtained.
Carrying out the correct computation of XOR function in neural network, it has been shown that QNN requires the proper correlation between the input and output qubits and the presence of appropriate entanglement in the system guarantees this correlation. It has been emphasized that the newly constructed maximally entangled two-qubit states, constituting new eigen basis, may be the most appropriate choice for utilizing entanglement in quantum neural computation. It has been shown that in quantum approach to neural networks all patterns can be stored as a superposition, where each of the patterns can be considered as existing in a separate quantum universe. It has also been shown that in neural networks the integrity of a stored pattern (bases states) is due to entanglement and the quantum associate memory (Qu AM) is the realization of the extreme condition of many Hopfield networks each storing a single pattern in parallel quantum universes.
2. Theoretical Basis of Quantum Computing
At quantum level an electron can be in a superposition of many different energy states, which is not possible classically. Similarly, any Physical system is described by quantum state
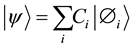 (2.1)
(2.1)
which is a linear superposition of basis states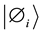 . Such a state is a Coherent State. This superposition is destroyed on interaction of system with its environment, i.e. it becomes decoherent.
. Such a state is a Coherent State. This superposition is destroyed on interaction of system with its environment, i.e. it becomes decoherent.  gives the probability of
gives the probability of 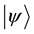 collapsing in to state
collapsing in to state 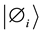 as it decoheres.
as it decoheres.
Electron-spin is a two state system with elements  corresponding to spin-up and
corresponding to spin-up and 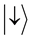 corresponding to spin-down. A state of this system may be written as
corresponding to spin-down. A state of this system may be written as
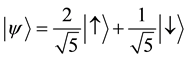 (2.2)
(2.2)
As long as system maintains coherence, it cannot be said to be in either spin-up or spin-down. When it decoheres, it can be in either of these states. Such a simple two- state quantum system is the basic unit of quantum computation: quantum-bit (qu-bit) where we rename two states as 0-state, and 1-state. Smallest unit of information stored in a two-state quantum computer is called a qu-bit. If there is a system of m qu-bits, it can represent 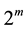 states at the same time.
states at the same time.
Qubit is simply a two-level system with generic state as
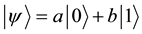 , (2.3)
, (2.3)
a two-dimensional complex vector, where a and b are complex coefficients specifying the probability amplitudes of corresponding states such that
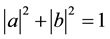
Qubit individual is defined by a string of qubits. An operator on a Hilbert space describes how one eigen state is changed into other. Thus a quantum operator is a q-gate and represented by a square matrix.
State of a qubit can be changed by the operation with a quantum gate which derives the individuals towards better solution (eventually towards a single state). A quantum gate is a reversible gate and can be represented as a unitary matrix U acting on a qubit basis state. Q-gates operating on just two bits at a time are sufficient to construct ageneral quantum circuit (based on Lie-Grouptheory). Thus quantum operator may be made [28] to work as NOT gate; controlled NOT gate (C-NOT); Rotation-gate; Hadmard-gate, etc.
Wave-peaks in phase interfere constructively and those out of phase destructively
Let 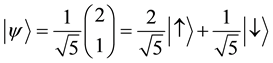
and an operator represented by matrix
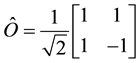
Then we have
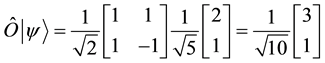

ÞAmplitude of  has increased while that of
has increased while that of 
Quantum Computation (QC) can be defined as representing the problem to be solved in the language of quantum states and producing operators that derive the system to a final state such that when system is observed there is high probability of finding a solution. QC consists of state preparation; useful time evolution of quantum system; and measurement of the system to obtain information. Upon measurement system will collapse to a single basis state. Object of QC is to ensure that measured basis state is with high probability. There are three different approaches to state preparation, based on information in set T of (n + 1) two states quantum systems (

1) Inclusion, 2) Exclusion, 3) Phase Inversion.
Inclusion is most intuitive where basis states not in T have zero coefficients and those in T have non-zero coefficients in the superposition:

Exclusion is an opposite approach, where basis state in T has zero coefficients and those not in T have non-zero coefficients in the superposition:

In Phase Inversion all basis states are included with coefficients of equal amplitudes but with different phases based on membership in T:

After state preparation, the pattern classification may be performed in straight forward approach employing the method of Grover’s [3] iterate which is described as a product of unitary operators GR applied to quantum state iteratively and probability of desired result maximized by measuring the system after appropriate number of iterations. Here the operator R is phase inversion of the state (s) that we wish to observe upon measuring the system. It is represented by identity matrix I with diagonal elements corresponding to desired state (s) equal to −1 and the operator G described as an inversion about average:
If 

Let us consider the case of n = 2 and T = {(001), (111)}. Then we have

and
where
Here probability 
highest conditional probability 

Requirements for Implementation of Quantum Computation
For implementing quantum computation there are following five requirements:
1) A scalable system with well characterized qubits;
2) Ability to initialize the state of qubits to a simple feudal state
3) Long relevant decoherence time (longer than gate operation time);
4) A universal set of quantum gates;
5) A qubit-specific measurement capability;
For quantum communication there are two more requirements;
1) Ability to interconvert stationary and flying qubits;
2) Ability to faithful transmit flying qubits between specific locations.
3. Entanglement
It is the correlation that can exist between different qu-bits (very little understood). When superposition is destroyed, the proper correlation is communicated between the qu-bits. It is this correlation that is the crux of entanglement.
Mathematically, it is described using density matrix formulation.
Density matrix of state 

The state for which density matrix cannot be factorized is said to be entangled while those with fully factorized density matrix are not entangled at all. For instance, let us consider a two-qubit state
which appears in matrix form as

where “1” denotes the presence of the corresponding eigen state in the superposition and ‘0’ denotes its absence, i.e. “1” for 






which cannot be factorized at all and the state 
Let us now consider the following quantum state as superposition of qubits 

or 
Its density matrix is

which is completely factorized. This state is not entangled at all.
Another quantum state with as superposition of qubits with least Hamming spread may be written as

with density matrix

which is fully factorized.
On the other hand the quantum state as superposition of qubits



Its density matrix is
which can be only partially factorized as

and hence the state is partially entangled. Thus the degree of entanglement for a two-qubit state depends on the extent of fractionalization of its density matrix and the entanglement is completely quantum phenomena without classical analogue.
It may readily be shown that the density matrix for the following two-qubit states (Bell States) cannot be factorized at all;




And hence all these states are maximally entangled states (MES). The matrices of these states satisfy the condition
or 
The states given by Equation (3.8) also satisfy the condition

These Equations (3.9) and (3.10) show that the states, given by Equation (3.8), constitute the orthonormal complete set and hence form the eigen-basis (magic basis) of the space of two level qubits. These states are maximally entangled states (MES) and also the eigen states of the unitary operator

where 



where


and 
For pure state 
with its concurrence defined as [19]

If the concurrence


For
the state 
The concurrence of a state is as reliable measure of degree of entanglement as the extent of factorization of its density matrix while Hamming spread of a two-qubit state is not that reliable measure of the entanglement since the states 



In terms of Z-components of spins of two electrons, the states 

and 
which consists of qubits with anti-parallel spins. On the other hand, the states 

and 
with one combination of parallel spins and other of anti-parallel spins. In states 

Various qubits of two-qubit states may be written as follows in magic basis;

4. Necessary and Sufficient Conditions for a Two-Qubit State to Be MES
A general two-qubit state may be written as

where 
Using the relations (3.19), this state may be written as

and using relation (3.15), its concurrence becomes

Thus for non-entangled state (i.e. separable state), we have

and for partially entangled states,

For MES, we have
or 
which can be true either for

or for 
These are the necessary conditions for the state 

and 
Bell states (i.e. magic bases) given by Equation (3.8) may readily be obtained from the state 

For these sets of values of a and b, the state 


tated by 



Other maximally entangled two-qubit states which form the orthonormal complete set (i.e. eigen bases) may be obtained as follows by putting 








with their density matrices respectively given by

None of which can be factorized at all. The concurrence for each of these states is unity and these states constitute the orthonormal set since
And
Other six MES obtained from 



States given by Equation (4.11) also constitute the eigen basis (different from magic basis given by Equation (3.8)) of the space of two-qubit system. In this basis, various qubits of two-qubit states may be written as

Substituting these relations in Equation (3.8), Bell states may be constructed as follows in this basis;

Concurrence of each of Bell states in this basis also is unity showing the invariance of concurrence in different bases.
Condition (4.6) for partial entanglement shows that if any coefficient of qubits in the state 
uation (4.1) is vanishing, then the state is necessarily partially entangled and its concurrence is 
squares of moduli of non-zero coefficients is 3. For instance, let

currence given by Equation (4.4) becomes 


are partially entangled with concurrence
5. Quantum Artificial Neural Network (QNN)
We have following motivations for applying capabilities of quantum computation to neural networks.
1) To compensate for ever decreasing scale in hardware development;
2) To produce computational capability not available using classical neural computation;
3) Recent Demonstration of superiority of Quantum Neural Network (QNN) over Classical ones [14] -[19] where the entanglement as learning rule plays as major role.
In Quantum neural computing, the phenomenon of entanglement can be viewed as playing arole similar to that of weighted connections in the classical neural network, producing correlations between different parts of the system. The quantum computational systems that make use of entangled states have the potential functionality of quantum neural networks (QNN). For instance, let us consider the entangled three-qubit state

which can be interpreted as computing the XOR function [19] , where the first two qubits encode the input and the third encode the output. The requisite correlations for computing the function are encoded in the entanglement of the state. Computing the value for the input x requires forcing the first two qubits to have unit probability of being found in the basis state 


The probability of finding the input in the state 


followed by the operator

is operated upon the state 


Thus the correct computation of XOR function requires the proper correlation between the input and output qubits. The presence of appropriate entanglement in the system guarantees this correlation. For entangled quantum states local operations on some qubits affect the states of all qubits in the system. Maximally entangled two-qubit states, constructed in Section 4, are the most appropriate choice for utilizing entanglement in quantum neural computation.
Two main difficulties faced in the implementation of QNN are related with linearity of quantum theory (while neural-computing depends upon non-linear data processing) and unitarity of evolutionary operators in quantum mechanics (while the pattern recall problem in QNN is equivalent to a search of a random data base). In the case of storage algorithm, evolution processes are a necessity (since the system must maintain a coherent superposition that represents the stored pattern) but requiring the recall mechanism to be evolutionary will limit the efficiency with which the recall may be accomplished and hence the recall is needed through non-evolutionary (i.e. non- unitary) process. These difficulties may be removed in the many universe interpretation of quantum mechanics, where decoherence or collapse of wave-function is only an illusion and the effect of measurement is split in to a number of copies each observing just one of the possible results of the measurement, unaware of the other possible outcomes. In this approach, there exist many mutually unobservable but equally real universes, each corresponding to a single possible outcome of the measurement and correlating through maximally entangled states. This combines the field of ANN with quantum computation in a natural way.
Hopfield neural network is best suited for the extraction of the locally most plausible version of a single prototype. If we generate multiple classical Hopfield networks which store only one pattern each, we lose any parallelism in processing the information. But in quantum approach, we can store all patterns as the quantum superposition

where each of the patterns p can be considered as existing in a separate universe. Interaction of a superposition with the environment is performed in parallel. Each of the basis states in superposition will play the role of a single memory state independent of the number of them that exist in superposition.
6. Discussion
Entanglement has been explored as one of the key resources required for quantum computation, the functional dependence of the entanglement measures on spin correlation functions has been established and the role of entanglement in implementation of QNN has been emphasized. Equations (3.3), (3.5), (3.6a) and (3.7a) show that the degree of entanglement for a two-qubit state depends on the extent of fractionalization of its density matrix and that the entanglement is completely a quantum phenomenon without any classical analogue. Equations (3.9) and (3.10) show that the maximally entangled Bell states, given by Equation (3.8), constitute the orthonormal complete set and hence form the eigen basis of the space of two-qubit states. These states have also been shown to be the eigen states of the unitary operator, defined by Equation (3.11), with the corresponding eigen values given by Equation (3.13). A reliable measure of entanglement of two-qubit states has also been expressed in terms of concurrence defined by Equation (3.15) and it has been shown by Equations (3.17) and (3.18) that in a free two-qubit system the states with both combinations of parallel spins (i.e. states with maximum Hamming spread) are definitely maximally entangled states (MES) while among the states with minimum Hamming spread, those with both anti-parallel combinations are MES and those with one combination of parallel spins and other with anti-parallel spins are not entangled at all. Equation (3.19) represents various qubits of two-qubit states in magic bases. Equation (4.7) gives the necessary and sufficient conditions for the general state, given by Equation (4.1), to be maximally entangled state. Equation (4.5) gives the condition for this state to be non-entangle (i.e. separable) while (4.6) gives the condition for this state to be partially entangled. Equations (4.8) and (4.9) give two different sets of maximally entangled two-qubit states, where it has been demonstrated that Bell states may be obtained from the state of Equation (4.8) by substituting



been shown to produce Bell states 




rotated by
Equation (4.10) gives other MES, different from Bell states, forming the orthonormal complete set (i.e. eigen basis) and it has been shown that, besides these two sets, there is no other orthonormal complete set of MES in two-qubit systems. Thus the set of Bell states is not the only eigen basis (magic eigen basis) of the space of two- qubit system, the set of MES given by Equation (3.10) also constitutes a very powerful and reliable eigen basis of two-qubit systems. This is the new eigen basis, being introduced for the first time, and to differentiate it from the already known Bell’s bases, let us call it Singh-Rajput basis for its possible use in future in the literature. The MES constructed in form given by Equation (4.10) may be correspondingly called Singh-Rajput states which generate Bell’s States in the form given by Equation (4.12). In terms of these states, all the qubits of two-qubit system may be obtained in terms of Equation (4.11). For symmetry purpose, for establishing functional dependence of entanglement on spin operators of qubits constituting MES and for the representations of SU(2) group and three dimensional rotation group, the use of these states may be more convenient. These possibilities will be demonstrated in our forthcoming papers.
Equations (5.1) and (5.4) demonstrate that the correct computation of XOR function in QNN requires the proper correlation between the input and output qubits. The presence of appropriate entanglement in the system guarantees this correlation. For entangled quantum states, local operations on some qubits affect the states of all qubits in the system. Maximally entangled two-qubit states (Singh-Rajput States), constructed in Section 4, may be the most appropriate choice for utilizing entanglement in quantum neural computation. In quantum approach to neural networks, all patterns can be stored as superposition given by Equation (5.5), where each of the patterns p can be considered as existing in a separate quantum universe. In this quantum analogue of Hopfield neural network, the integrity of a stored pattern (basis states) is due to entanglement. It leads to all known quantum algorithms. Quantum associate memory (Qu AM) is the realization of the extreme condition of many Hopfield networks, each storing a single pattern in parallel quantum universes.
Cite this paper
Manu P.Singh,B. S.Rajput, (2015) Role of Entanglement in Quantum Neural Networks (QNN). Journal of Modern Physics,06,1908-1920. doi: 10.4236/jmp.2015.613196
References
- 1. Feynman, R.P. (1982) Simulating Physics with Computers. International Journal of Theoretical Physics, 21, 467-488.
http://dx.doi.org/10.1007/BF02650179 - 2. Shor, P.W. (1994) Algorithms for Quantum Computation: Discrete Logarithm and Factoring. Proceedings of 35th Annual Symposium on Foundations of Computer Science, Santa Fe, 20-22 November 1994, 124-134.
http://dx.doi.org/10.1109/sfcs.1994.365700 - 3. Grover, L.K. (1996) A Fast Quantum Mechanical Algorithm for Data Base Search. Proceedings of 28th Annual ACM Symposium on Theory of Computing, Philadelphia, 22-24 May 1996, 212-219.
- 4. Simon, D. (1997) On the power of Quantum Computation. SIAM Journal on Computing, 26, 1474-1483.
- 5. Ventura, D. and Martinez, T. (1999) Initializing Amplitude Distribution of a Quantum State. Foundations of Physics Letters, 12, 547-559.
http://dx.doi.org/10.1023/A:1021695125245 - 6. Zak, M. (2000) Quantum Decision-Maker. Information Sciences, 128, 199-215.
http://dx.doi.org/10.1016/s0020-0255(00)00053-0 - 7. Bshouty, N.H. and Jackson, J. (1995) Learning DNF over the Uniform Distribution Using a Quantum Example Oracle. Proceedings of the 8th Annual Conference on Computational Learning Theory, Santa Cruz, 5-8 July 1995, 118-127.
- 8. Li, S.S. and Huang, Y.B. (2008) Entanglement of Superposition of Multistates. International Journal of Quantum Information, 6, 561-565
- 9. Li, S.S., Nie, Y.Y., Hong, Z.H., Yi, X.J. and Huang, Y.B. (2008) Controlled Teleportation Using Four-Particle Cluster State. Communications in Theoretical Physics, 50, 633-640
- 10. Huang, Y.B., Li, S.S. and Nie, Y.Y. (2009) Controlled Dense Coding between Multi Particles. International Journal of Theoretical Physics, 48, 95-100.
http://dx.doi.org/10.1007/s10773-008-9785-z - 11. Li, S.S. (2012) Dense Coding with Cluster State Via Local Measurements. International Journal of Theoretical Physics, 51, 724-730.
http://dx.doi.org/10.1007/s10773-011-0951-3 - 12. Wang, Z.S., Wu, C., Feng, X.L., Kwek, L.C., Lai, C.H., Oh, C.H. and Vedral, V. (2007) Nonadiabatic Geometric Quantum Computation. Physical Review A, 76, Article ID: 044303. http://dx.doi.org/10.1103/PhysRevA.76.044303
- 13. Wang, Z.S. (2009) Geometric Quantum Computation and Dynamical Invariant Operators. Physical Review A, 79, Article ID: 024304.
http://dx.doi.org/10.1103/PhysRevA.79.024304 - 14. Narayanan, A. and Meneer, T. (2000) Quantum Artificial Neural Network Architectures and Components. Information Sciences, 128, 231-255.
http://dx.doi.org/10.1016/S0020-0255(00)00055-4 - 15. Behrman, E.C., Nash, L.R., Sleck, J.E., Chandrashekhar, V.G. and Skinner, S.R. (2000) Simulations of Quantum Neural Networks. Information Sciences, 128, 257-269.
http://dx.doi.org/10.1016/s0020-0255(00)00056-6 - 16. Ventura, D. and Martinez, T. (2000) Quantum Associative Memory. Information Sciences, 124, 273-296.
http://dx.doi.org/10.1016/S0020-0255(99)00101-2 - 17. Ezkov, A., Nifanava, A. and Ventura, D. (2000) Quantum Associative Memory with Distributed Queries. Information Sciences, 128, 271-293.
http://dx.doi.org/10.1016/S0020-0255(00)00057-8 - 18. Howell, J., Yeazell, J. and Ventura, D. (2000) Optically Simulating A Quantum Associative Memory. Physical Review A, 62, Article ID: 042303.
http://dx.doi.org/10.1103/PhysRevA.62.042303 - 19. Ventura, D. and Martinez, T. (1999) Initializing the Amplitude Distribution of a Quantum State. Foundations of Physics Letters, 12, 547-559.
http://dx.doi.org/10.1023/A:1021695125245 - 20. Jennewein, T., Simon, C., Weihs, G., Weinfurter, H. and Zeilinger, A. (2000) Quantum Cryptography with Entangled Photons. Physical Review Letters, 84, 4729-4732.
http://dx.doi.org/10.1103/PhysRevLett.84.4729 - 21. Naik, D.S., Peterson, C.G., White, A.G., Burglund, A.J. and Kwiat, P.G. (2000) Entangled State Quantum Cryptography: Eavesdropping on the Ekert Protocol. Physical Review Letters, 84, 4733-4736.
http://dx.doi.org/10.1103/PhysRevLett.84.4733 - 22. Tittel, W., Bendel, J., Zbinden, H. and Gisin, N. (2000) Quantum Cryptography Using Entangled Photons in Energy-Time Bell States. Physical Review Letters, 84, 4737-4740.
http://dx.doi.org/10.1103/PhysRevLett.84.4737 - 23. Tan, H.T., Zhang, W.M. and Li, G. (2011) Non-Markovian Dynamics of an Open Quantum System with Initial System-Reservoir Correlations: A Nanocavity Coupled to a Coupled-Resonator Optical Waveguide. Physical Review A, 83, Article ID: 032102.
http://dx.doi.org/10.1103/PhysRevA.83.032102 - 24. Smirne, A., Breuer, H.P., Piilo, J. and Vacchini, B. (2010) Initial Correlations in Open-Systems Dynamics: The Jaynes-Cummings Model. Physical Review A, 84, Article ID: 062114.
http://dx.doi.org/10.1103/PhysRevA.82.062114 - 25. Benenti, G. and Casati, G. (2009) How Complex Is Quantum Motion? Physical Review E, 79, Article ID: 025201.
http://dx.doi.org/10.1103/PhysRevE.79.025201 - 26. Hill, S. and Wooters, W.K. (1997) Entanglement of a Pair of Quantum Bits. Physical Review Letters, 78, 5022-5025.
http://dx.doi.org/10.1103/PhysRevLett.78.5022 - 27. Wooters, W.K. (1998) Entanglement of Formation of an Arbitrary State of Two Qubits. Physical Review Letters, 80, 2245-2248.
http://dx.doi.org/10.1103/PhysRevLett.80.2245 - 28. Monvol, C., Meekhof, D.M., King, B.E., Itano, W.M. and Wineland, D.J. (1995) Demonstration of a Fundamental Quantum Logic Gat. Physical Review Letters, 75, 4714-4718.
http://dx.doi.org/10.1103/PhysRevLett.75.4714
NOTES
*Corresponding author.















