Received 22 January 2015; accepted 26 April 2015; published 29 April 2015

ABSTRACT

Reflection symmetry properties play important roles for the stability of crystal lattices in which electrons and phonons move. Based on the reflection symmetry properties, cubic, tetragonal, orthorhombic, rhombohedral (trigonal) and hexagonal crystal systems are shown to have three- dimensional (3D) k-spaces for the conduction electrons (“electrons”, “holes”). The basic stability condition for a general crystal is the availability of parallel material planes. The monoclinic crystal has a 1D k-space. The triclinic has no k-vectors for electrons, whence it is a true insulator. The monoclinic (triclinic) crystal has one (three) disjoint sets of 1D phonons, which stabilizes the lattice. Phonons’ motion is highly directional; no spherical phonon distributions are generated for monoclinic and triclinic crystal systems.

Keywords:

k-Vectors, Conduction Electron, Reflection Symmetry, Crystal Structure, Lattice Stability

1. Introduction

In 1956 Lee and Yang published a historic paper [1] on the parity non-conservation for neutrinos after examining the space inversion 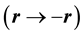property of massless Dirac’s relativistic wave equation. Inversion and reflection symmetry properties are also important in solid state physics. They play important roles for the stability of crystal lattices in which electrons and phonons move. Based on the reflection symmetry properties, we show that the monoclinic (MCL) has a one-dimensional (1D) k-space, and the triclinic (TCL) has no k-vectors for electrons. If parallel material planes exist for a crystal lattice, then phonons can be generated, and they can stabilize the lattice. A TCL crystal has three disjoint sets of 1D nonorthogonal k-vectors. Phonons’ motion is highly directional, and there are no spherical waves formed.

2. Electrons

Following Ashcroft and Mermin (AM) [2] , we assume that electrons and holes in solids run as wave packets (not point-particles). We adopt the semiclassical model of electron dynamics in solids [2] . It is necessary to introduce a k-vector:

(1)

where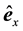, , 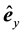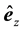are the orthonormal vectors, since the k-vectors are involved in the semiclassical equation of motion:

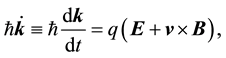(2)

where 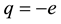is the electron charge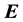, and and 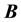are the electric and magnetic fields, respectively. The vector

(3)

is the electron velocity, where 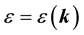is the energy.

If the electron is in a continuous energy range (energy band), then it will be accelerated by the electric force, and the material is a conductor. If the electron’s energy is in a forbidden band (energy gap), it does not move under a small electric force, and the material is insulator. If the acceleration occurs only for a mean free time (inverse of scattering frequency)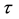, the conductivity 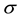for a simple metal is given by Drude’s formula [2] :

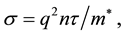(4)

where n is the electron density and 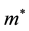the effective mass.

For some crystals such as simple cubic (SC), face-centered cubic (FCC), body-centered-cubic (BCC), tetragonal (TET) and orthorhombic (ORC) crystals, the choice of the orthogonal -axes and the unit cells is obvious. The 2D crystals can also be treated similarly, only the z-component being dropped.

Let us consider an ORC crystal with sides. This crystal is reflection-symmetric about yz-, zx- and xy-plane which intersect at the origin. The lattice potential is triply reflection-symmetric:

(5)

The Brillouin zone boundary forms an orthogonal hexahedron with sides. The electron- energy is quadratic in near the origin:

(6)

where are effective masses. To deal with the reflection symmetry, it is necessary and essential to introduce the Cartesian coordinates. The TET and SC crystals can be treated similarly.

There are seven (7) crystal systems, see e.g. AM’s book [2] . They are: cubic (CUB), TET, ORC, rhombohedral (RHL), hexagonal (HEX), MCL, and TCL systems. Arsenic (As) and Bismuth (Bi) form RHL crystals. A RHL crystal can be obtained by stretching (or contracting) the three body-diagonals from a SC crystal. But the body-diagonal directions remain orthogonal to each other for any stretching. Hence, if an orthogonal unit cell with the Cartesian axes along the body diagonals is chosen, then the system is periodic along the x- and y-, and z-axes passing the center. Thus, the RHL system can be treated as an ORC crystal, and hence it has a 3D k-space spanned by 3D k-vectors. Diamond (C) and silicon (Si) form diamond (DIA) crystals. A DIA lattice can be decomposed into two FCC sublattices, and can therefore be treated similarly as a CUB crystal. A number of elements including graphite form HEX crystals. HEX crystals can be treated similar to ORC crystals by choosing orthogonal unit cells. See below for the case of graphite.

We consider a graphene which forms a 2D honeycomb lattice. The Wigner-Seitz (WS) unit cell, a rhombus (darkened area) shown in Figure 1(a), contains two C’s. We showed in our earlier work [3] that graphene has “electrons” and “holes” based on the rectangular unit cell (dotted lines) shown in Figure 1(b). We briefly review our calculations below. More details can be found in Refs. [3] [4] .

We assume that the “electron” (“hole”) wave packet has the charge and a size of the rectangular unit cell, generated above (below) the Fermi energy. We showed [3] that (a) the “electron” and “hole” have different charge distributions and different effective masses, (b) that the “electrons” and “holes” move in different easy channels, (c) that the “electrons” and “holes” are thermally excited with different activation energies, and (d) that the “electron” activation energy is smaller than the “hole” activation energy:

(7)

Hence, “electrons” are the majority carriers in graphene. The thermally activated electron densities are given by

(8)

where and 2 represent the “electron” and “hole”, respectively. Magnetotransport experiments by Zhang et al. [5] indicate that the “electrons” are majority carriers in graphene in agreement with our theory.

Graphite is composed of graphene layers stacked in the manner ABAB ××× along the -axis. We may choose an orthogonal unit cell shown in Figure 2. The unit cell contains 16 C’s. The two rectangles (white solid lines) are stacked vertically with the interlayer separation, c₀ = 3.35 Å, much greater than the nearest neighbor distance between two C’s, a₀ = 1.42 Å:

(9)

The unit cell has three side-lengths:

(10)

Clearly, the system is periodic along the orthogonal directions with the three periods given in Equation (10). In summary, the system is orthorhombic with the sides, , ,.

The negatively charged “electron” (with the charge) in graphite are welcomed by the positively charged C⁺ when moving vertically up or downwards in the plane. That is, the easy directions for the “electrons” are vertical. The easy directions for the “holes” are horizontal. There are no hindering hills for “holes” moving horizontally. Hence, the “electron” in graphite has the lower activation energy than the “hole”:. Then, “electrons” are the majority carriers in graphite. The thermoelectric power (Seebeck coefficient) measurements by Kang et al. [6] show that the majority carriers in graphite are “electrons”, which is in agreement with our theory.

The construction of the orthogonal unit cell developed here can be followed for other HEX crystals. Zinc (Zn) and Beryllium (Be) form HEX crystals.

A MCL crystal has a c-axis. It is reflection-symmetric with respect to the x-y plane perpendicular to the c-(z-)axis. It has only one-dimensional (1D) k-vectors along the c-axis. A TCL crystal has no reflection symmetry and then it has no k-vectors. Hence it is a true (intrinsic) insulator.

In summary, CUB, TET, ORC, RHL and HEX crystals have 3D k-space spanned by 3D k-vectors. MCL crystals have 1D k-space. TCL crystals have no k-vectors.

We take MCL vanadium dioxide VO₂. The z-axis is taken as the c-axis. In the x-y plane there is an oblique net whose corners are occupied by V’s. The position vector of every V can be represented by integers, if we choose the Bravais vector

(11)

where and are non-orthogonal base vectors. In the field theoretical formulation the field point is given by

(12)

where is the point defined within the standard unit cell. Equation (12) describes the 2D lattice periodicity but does not establish k-space as explained below.

To see this clearly, we first consider an electron in a simple square (sq) lattice. The Schrödinger wave equation is

(13)

The potential energy V is lattice-periodic:

(14)

(15)

If we choose a set of Cartesian coordinates for the sq lattice, then the Laplacian term in Equation (13) is given by

(16)

which is a key step for the separation-of-variables method of solution. If we choose a periodic square boundary with the side length, , then there are 2D Fourier transforms and 2D k-vectors.

We now go back to the original rhombic system. If we choose the x-axis along either or, then the potential energy field is periodic in the x-direction but it is aperiodic in the y-direction. For an infinite system the only acceptable boundary for the Fourier transformation is a periodic boundary condition. Hence, there is no 2D k-space for the rhombic system.

In summary, the five systems, CUB, TET, ORC, HEX, RHL, have inversion symmetry. The MCL has a mirror symmetry only with respect to the x-y plane. No reflection symmetry is found for a TRC crystal. The 2D honeycomb lattice has a reflection symmetry relative to the x- and y-axes as shown in Figure 1(b).

3. Phonons

Let us consider small oscillations for a system of atoms forming a SC lattice. Assume a longitudinal traveling wave along a cubic axis (x-axis). Imagine hypothetical planes perpendicular to the x-axis containing atoms forming a square lattice. This plane has a mass per unit square of side-length a (the lattice constant), equal to the atomic mass m. The plane is subjected to a restoring force per cm² equal to Young modulus Y. The dynamics of a set of the parallel planes are similar to that of the coupled harmonic oscillators.

Assume next a transverse wave traveling along the x-axis. The hypothetical planes containing many atoms are subjected to a restoring stress equal to the shear modulus S. The dynamics is also similar to the coupled harmonic oscillators in 1D.

Low-frequency phonons are those to which Debye’s continuum solid model [7] applies. The wave equations are

(17)

where (longitudinal) or t (transverse). The longitudinal-wave phase velocity is

(18)

where is the mass density. The transverse-wave phase velocity is

(19)

The waves are superposable. Hence, phonons’ travel are not restricted to the crystal’s cubic directions. In short, there is a 3D k-vector,. The wave propagation is isotropic.

Consider now the case of an ORC crystal. We may choose a Cartesian coordinate passing through the center of the unit cell. The small oscillations are similar to the case of a SC lattice. The dynamics of the parallel plates are similar but the restoring forces are different in x-, y-, z-directions. The plane waves have different phase velocities depending on the directions. They are superposable since these waves are still solutions of the wave Equations (17).

Phonons are quanta corresponding to the running plane-wave modes of the lattice vibrations. Phonons are bosons, and the energies are distributed, following the Planck distribution function:

(20)

There is no activation energy unlike the case of the “electrons”. This arises from the boson nature of phonons. The temperature T alone determines the average number and energy.

Phonons and conduction electrons are generated based on the same lattice- and k-spaces. This is important when describing the electron-phonon interaction.

The “electrons” and “holes” by postulate have the same orthogonal unit cell size. The phonon size is much greater than the electron size. The low-energy phonons have small k and great wavelengths. The average energy of a fermionic electron is greater than a bosonic phonon by two or more orders of magnitude. This establishes a usual picture that a point-like electron runs and is occasionally scattered by a cloud-like phonon in the crystal.

Earlier we saw that a MCL crystal has 1D k-vectors pointing along the c-axis for the electrons. There are similar 1D k-vectors for phonons. Besides, there are two other sets of 1D k-vectors. Plane waves running in the z-directions can be visualized by imagining the parallel plates, each containing a great number of atoms executing longitudinal and transverse small oscillations. Plane-waves proceeding upward or downward exist. Consider an oblique net of points (atoms) viewed from the top shown in Figure 3. Planes defined by the vector and the z-axis are parallel and each plane contains a great number of atoms. Planes defined by the vector and the c-axis are parallel, and each contains a number of atoms also executing small oscillations. These three sets of 1D phonons stabilize the lattice.

We next consider a TCL crystal, which has no k-vectors for electrons. Turquoise (bluish green gem) forms a TCL crystal. There are, however, three sets of 1D k-vectors for phonons. Take a primitive TCL unit cell. The opposing faces are parallel to each other. There are restoring forces characterized by Young modulus Y and

shear modulus S. Then, there are 1D k-vectors perpendicular to the faces. These sets of 1D phonons can stabilize the lattice. These phonons in TCL are highly directional. There are no spherical waves formed.

We used the lattice property that the facing planes are parallel. This parallel-plane-translation-invariant property is common to all seven crystal systems. A typical HEX system, graphite, shown in Figure 2, clearly has three sets of parallel material planes containing many atoms. The RHL system has similar parallel planes, too. The parallel material planes configuration is the basic condition for the phonon generation. These phonons stabilize the crystal.

4. Conclusions

In summary, we established based on the reflection symmetry properties of crystals that

Ÿ The parallel material-plane configuration is the basic condition for phonon generation and lattice stability.

Ÿ CUB, TET, ORC, RHL, HEX crystal systems have 3D k-spaces for electrons. The MCL system has a 1D k-space. The TCL has no k-vectors.

Ÿ The MCL and TCL have 1D phonons which are highly directional. No spherical phonon distributions are generated.

Ÿ For RHL and HEX crystals the orthogonal unit cells different from the WS primitive cells must be chosen for electron dynamics.

Ÿ “Electrons” and “holes” have the same unit cell size, and they move with different effective masses in general. “Electrons” and “holes” in semiconductors are excited with different activation energies. Phonons are generated without activation energies.

Ÿ Both phonons and electrons are generated based on the same orthogonal unit cells. This fact is important when dealing with the electron-phonon interaction.

Ÿ Both electrons and phonons move as wave packets. The electron size is the primitive orthogonal unit cell size. The average phonon size is greater by two or more orders of magnitude at the room temperature.

References