ABSTRACT

We consider the AdS₅ × S⁵ integrable model. As it turns out, relying on well known arguments, we claim that the conformally invariant fermionic model is solvable, the resulting solution given in terms of two current algebras realizations.

Keywords:Component, Formatting, Style, Styling, Insert

1. Introduction

Integrable models have a long and successful history [1] . In particular, models defined on a symmetric space are generally integrable [2] -[4] . This means that an infinite number of local conservation laws exist [2] , or at least one nonlocal conservation law [1] [5] . In general, such integrable models display a non vanishing mass gap, useful for describing the exact S-matrix in terms of rapidities [3] [6] . In such a line, a large number of models have been solved and their exactness on shell solution was obtained [7] -[10] .

There is also at least one model where no mass gap exists, but comprising non trivial conservation laws. It is the case of the chiral Gross-Neveu model [11] . Supposing the existence of a mass gap, the model has been solved on shell [12] [13] . However, it is known that there is a non trivial fix point such that the theory allows for a conformally invariant solution as well, for a given value of the coupling constant [14] .

This means that an integrable model can also contain a conformally invariant solution. This is a quite non trivial fact that we wish to explore in case of integrable models relevant for string theory, where conformal invariance is a very desirable property.

In the framework of string theory, it is possible to gather information about the Yang-Mills theory at intermediate coupling. Obtaining a strongly coupled field theory underlying the QCD string actually provides an integrable model in the world sheet, and the low dimensionality of the problem may imply exact solvability [15] .

In that case, the symmetry of the integrable model is.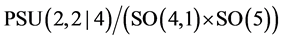

The bosonic part of such a coset is AdS₅ × S⁵, which will be our main concern. Most of the literature is related, in this case, to integrable models and their nonlocal conservation laws [16] [17] . Currents for the pure spinor superstring in AdS₅ × S⁵ have subsequently been constructed [18] . While the role of AdS₅ is largely discussed in relation to string solutions [19] [20] , integrable structures are related to the underlying string spectrum [21] .

Later, the non local charges have also been related to a BRST cohomology [22] ensuring κ-symmetry. One thus conjectured that conformal invariance should be related to the integrable models relevant to string theory.

On the other hand, in string theory, a lot has been done concerning integrability of the underlying symmetry of strings in certain backgrounds. In Maldacena’s conjecture, four-dimensional N = 4 super Yang-Mills theory is dual to super strings in AdS₅ × S⁵ background [23] . But

(1)

This means that the model is defined on a symmetric space, thus implying a non trivial (and non local) conservation law [2] . Moreover, since the symmetric space is a direct product of symmetric spaces with simple gauge groups, the sigma model defined on that space is also integrable at the quantum level [4] . On the other hand, conformal invariance is very useful in string theory and the question is whether these models display conformal invariance, at least in some form. The answer is positive, as we show.

We shall consider a fermionic model defined upon the space (1). Following old and well established arguments we see that at a well defined value of the coupling constant the theory is conformally invariant.

2. Conserved Currents

The above mentioned fermionic model is defined by the lagrangian density

(2)

where we define the currents are given by 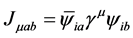and. They are related to the first or second factors defining the underlying symmetry group, that is, we identify the labels 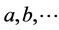as being in SO(5,1) and 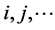in SO(6). Here, g₁ and g₂ are, up to now, arbitrary coupling constants.

The field equation for is

(3)

while

(4)

is the field equation for.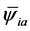

The Noether currents related to the symmetries SO(5,1) and SO(6), respectively, obey the conservation equations and.

Let us now consider the axial currents (non) conservation laws. Using the relations for the γ_{μ} matrices we have

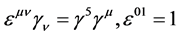
(5)

(6)

We can compute the divergence of the axial current,

,

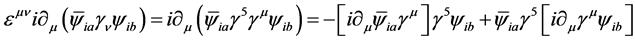(7)

Taking into account the field equations we get

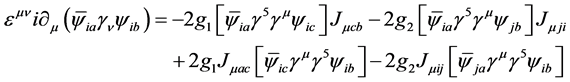(8)

Here we note that the terms with the g₁ coefficient are products of two currents while the terms with g₂ coefficient are cancelled, that is,

(9)

Using the identity

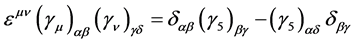(10)

the final result is

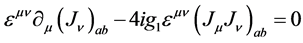(11)

Therefore, the axial current fails to be conserved classically.

A similar result follows for the axial current,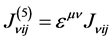

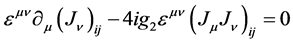(12)

We consider now the axial anomaly contribution to the field equations. We introduce the gauge field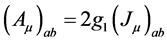 in order to identify the anomaly term

(13)

to be added to the divergence equation for,

(14)

where N is the number of species, in this case equal to 6. We are thus led to

(15)

Therefore, the choice implies that the axial current is also conserved,

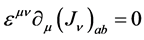(16)

This means conformal invariance in the coset SO(5,1)/O(4,1). Notice that, mutatis mutandis we get similar a result for the SO(6)/O(5) factor, as well as conformal invariance for all spaces of the kind in case we carefully choose the coupling. Thus, at the point the second axial current is conserved

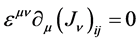(17)

and the fermionic theory in the coset SO(6)/(O(5) is conformally invariant.

An alternative and equivalent proof of conformal invariance at a given coupling can be obtained by arguments already known in [14] . Thus, for these values of g₁ and g₂ we get the conformal field 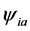with SO(5,1)/ SO(4,1) × SO(6))/SO(5) conformal invariance.

3. Currente Algebra

We can write the equal-time commutation rules

(18)

where C₁ and C₂ (= 0 or − C₁) are c-number Schwinger terms. In addition, we also have

(19)

where D₁ and D₂ (= 0 or − D₁) are also c-number Schwinger terms.

Here we note the structure constants of the factor group SO(5,1)/O(4,1) and of SO(6)/O(5).

Using

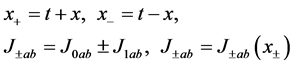(20)

we can deduce from the equal-time commutation relations the commutation rules for any space-time point,

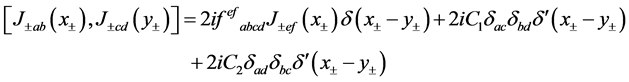(21)

We can now decompose also the currents into creation and annihilation parts, each one of massless excitations. We have

(22)

where (+) is the creation part and (‒) the annihilation part. Note that here two creation or two annihilation operators of different SO(5,1)/O(4,1) indices do not commute.

One finds also

(23)

where, due to Jacobi identity and. A similar construction with the current can be trivially obtained.

Correlation functions are now immediately obtained from the methods of two-dimensional conformally invariant Quantum Field Theory [1] .

The by now rather expected results displayed above mean that integrable models can have a conformally invariant counterpart. The fact that in string theory one needs conformal invariance as a building block forces us into the above solution at least for the fermionic models in question.

The rather important unanswered question is about what happens in case of a purely bosonic theory, or also, maybe even more important, to the model defined on a graded manifold. In the last case, in view of the unbroken supersymmetry, we are led to a conjecture concerning such sigma models, namely we conjecture that such models have a conformal fix point where the correlators are exactly solvable and present the previous symmetry.

Acknowledgements

This work has been supported by FAPESP and CNPq, Brazil.

References