Journal of Modern Physics
Vol.04 No.02(2013), Article ID:28348,13 pages
10.4236/jmp.2013.42039
Quantum Gravity in Heisenberg Representation and Self-Consistent Theory of Gravitons in Macroscopic Spacetime
Grigory Vereshkov1,2, Leonid Marochnik3
1Research Institute of Physics, Southern Federal University, Rostov-on-Don, Russia
2Institute for Nuclear Research of the Russia Academy of Sciences, Moscow, Russia
3Physics Department, University of Maryland, East West Space Science Center, College Park, USA
Email: gveresh@gmail.com, lmarochnik@gmail.com
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received November 22, 2012; revised December 23, 2012; accepted December 31, 2012
ABSTRACT
The first mathematically consistent exact equations of quantum gravity in the Heisenberg representation and Hamilton gauge are obtained. It is shown that the path integral over the canonical variables in the Hamilton gauge is mathemati- cally equivalent to the operator equations of quantum theory of gravity with canonical rules of quantization of the gravitational and ghost fields. In its operator formulation, the theory can be used to calculate the graviton S-matrix as well as to describe the quantum evolution of macroscopic system of gravitons in the non-stationary Universe or in the vicinity of relativistic objects. In the S-matrix case, the standard results are obtained. For problems of the second type, the original Heisenberg equations of quantum gravity are converted to a self-consistent system of equations for the me- tric of the macroscopic space time and Heisenberg operators of quantum fields. It is shown that conditions of the com- patibility and internal consistency of this system of equations are performed without restrictions on the amplitude and wavelength of gravitons and ghosts. The status of ghost fields in the various formulations of quantum theory of gravity is discussed.
Keywords:
Quantum Gravity

1. Introduction
In the works [1,2] it is shown that the observed acceler- ated expansion of the Universe (the Dark Energy effect) [3,4] may be a consequence of macroscopic effect of the quantum theory of gravity which is the condensation of gravitons on the horizon scale of the non-stationary Uni- verse. The theory of this macroscopic quantum effect is based only on the most general properties of quantum gravitational field in the non-stationary Universe, which are Bose-Einstein statistics, zero rest mass of gravitons, their conformal non-invariance and one-loop finiteness of quantum gravity off the graviton mass shell. (One- loop finiteness on the graviton mass shell was proved by T’Hooft and Veltman in 1974 [5].) In [1], three exact solutions of equations one-loop quantum gravity are pre- sented. They are presented in terms of moments of spec- tral function of gravitons which is renormalized by ghosts. These solutions describe three different phase states of the condensate. One of these solutions describ- ing the self-polarized condensate in the de Sitter space is represented in terms of field operators and state vectors. The effect of condensation is clearly demonstrated by the fact that the state vectors have the form of quantum co-
herent superposition of vectors corresponding to different occupation numbers of gravitons and ghosts having the same wavelength of the order of the radius of 4-curvature. Detailed analysis of all solutions is given in [2].
This work aims to show that the equations of one-loop quantum gravity obtained in [1] are the only mathemati- cally consistent of all in the available literature. As is known, the quantum gravity is non-renormalizable theory [6]. At the same time, once again we emphasize that the pure one-loop quantum gravity (without matter fields) is finite. The macroscopic quantum effects of interest are already occurring in the one-loop approximation. Our program is to obtain the equations of the one-loop theory of the formally (in mathematical sense) exact equations of quantum gravity. We believe that only such a way to obtain the one-loop equations allows conducting the cor- rect one-loop calculations that predict the condensation of gravitons on the horizon scale of the Universe.
For curvatures that are less than Planck curvature, quantum cosmology is represented as a theory of gravi- tons in the macroscopic space time with the self-consis- tent geometry. The quantum state of gravitons is deter- mined by their interaction with a macroscopic field, and
the macroscopic (background) geometry, in turn, de- pends on the state of gravitons. The background metric and graviton operator appearing in the self-consistent theory are extracted from the unified gravitational field, which initially satisfies exact equations of quantum grav- ity. The classical component of the unified field is a function of coordinates and time by definition. The quantum component of the same unified field is descri- bed by a tensor operator function, which also depends on coordinates and time. Under such a formulation of the problem, the original exact equations should be the ope- rator’s equations of quantum theory of gravity in the Heisenberg representation. The present work is devoted to obtaining such equations and their identity transforma- tion to the self-consistent system of classical and quan- tum equations with no restrictions on the wavelength and amplitude of the graviton field.
The Heisenberg representation of quantum theory can be introduced only by its Hamilton formulation. For the theory with constraints, we deal with a generalized Ham- ilton formalism. The generalized Hamilton formalism of the theory of gravity was constructed by Dirac [7,8] and Arnowitt, Deser and Misner [9]. There are also other formulations of theory that differ from [7-9] by parame- terization of gravitational variables. We use the formal- ism proposed by Faddeev [10] (see Section 5 in the re- view [11] or a book [12], §24). In the non-degenerate field theories and in the theories that allow to remove the degeneracy completely, the transition from the classical Hamilton theory to the quantum theory in the Heisenberg representation is reduced to a simple replacement of the classical Poisson brackets with the quantum commutators. Conducting of the same operations in the theory of grav- ity would be possible if the four local gauge conditions together with four equations of constraints in the theory, would completely determine physical degrees of freedom that are to be quantized. In the theory of gravity local gauges completely removing the degeneracy are un- known. Therefore, the question arises, whether there is a Heisenberg representation of quantum gravity in local gauges, if these gauges are unable to separate the true gravitational field from the fields of inertia? This paper gives a positive answer to this question. The important fact is that the transition from classical to quantum theory is not limited to the replacement of C-numeric functions with the operator functions satisfying the canonical com- mutation relations. Such a replacement must be accom- panied by the appearance of the operator functions of Faddeev-Popov ghosts (see Section 3).
At the present time, an operator version of equations proposed in [7-9] is usually considered as the equations of quantum gravity in the Heisenberg representation. One should, however, bear in mind that local gauge condi- tions used in [7-9] do not remove the degeneracy com- pletely, i.e. quantum fields of inertia are present in the equations of theory. Therefore, perturbative S-matrixes calculated in these theories do not satisfy the unitarity con- dition. As is known, the existence of this problem drew the attention of Feynman [13] in the analysis of the the- ory in the local covariant gauge which is convenient for perturbative calculations. Faddeev and Popov [14] sug- gested a regular method of unitary S-matrix calculation, based on introduction of the auxiliary ghost fields in the path integral. Any correct formulation of quantum theory of gravity should allow to calculate the graviton S-matrix as one of its objectives, and the result of this calculation should coincide with the Faddeev-Popov S-matrix.
Despite this fact, the operator Einstein equations in the Heisenberg representation with the local gauges (without ghosts) that do not remove the degeneracy completely and do not satisfy the test for unitarity S-matrix, were used in discussing of cosmological applications of quantum gravity, i.e. in the quantum theory of gravitons in the non-stationary Universe (see, e.g., [15,16]).
In connection with the situation that exists in the scientific literature, we emphasize the following circum- stance. Except the test on a unitarity of S-matrix, there is no other criterion of correctness of the equations of quan- tum gravity, and, as a consequence, the correctness of the results obtained from these equations. Therefore, the Ha- milton equations in the Heisenberg representation with the canonical quantization rules must be strictly deduced from the exact equations of quantum gravity satisfying the above test. In this paper, we show that these equa- tions do exist under condition that the Faddeev-Popov ghosts are among the elements of the Hamilton formal- ism of quantum gravity.
We obtain the Hamilton equations in the Heisenberg re- presentation by identity transformation of the path integral over the canonical variables. Such an integral was propo- sed by Faddeev [10] on the basis of the general theory of Hamilton systems with explicitly unsolvable constraints [17]. The ghost sector is originally contained in this inte- gral, and for this reason it will inevitably be present in the mathematically equivalent operator Hamilton equations.
The procedure for obtaining of these equations is as follows. In the first step, the gauge of Faddeev’s path in- tegral [10] is specified such that the ghost sector corre- sponding to it permits the introduction of canonical vari- ables of the ghost fields and the representation of ghost Lagrangian in the Hamilton form. In the second step, the standard definition of the operator of evolution is used, and a transition is made from the gauged path integral to the canonical Hamilton formalism in the Heisenberg representation. The canonical operator quantization ac- quires the status of a method which is a mathematical equivalent to the functional integration over the extended phase space of gravitons and ghosts.
The Heisenberg representation in the quantum theory of gravity (outside of perturbation theory) exists in the synchronous gauge in the normal coordinates. This gauge is an analogue of Hamilton gauge in the Yang-Mills the- ory. Basically, the operator Hamilton formalism with the canonical quantization of gravitational and ghost fields is to solve problems in quantum cosmology but can be also used for the calculation of S-matrix where it leads to standard results.
2. Classical Einstein Equations in Hamilton Gauge
2.1. Einstein Equations in Normal Coordinates
Upon obtaining of the exact equations of the theory of gravity in the Hamilton form, the gravitational field can be regarded as the deviation of the metric from the metric of Minkowski space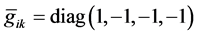 . Normal coordinates of gravitational field of
. Normal coordinates of gravitational field of 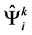 are given by exponential parameterization of the density of the con- travariant metric [18]
are given by exponential parameterization of the density of the con- travariant metric [18]
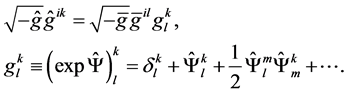 (1)
(1)
The density of the gravitational Lagrangian as a func- tion of normal coordinates reads
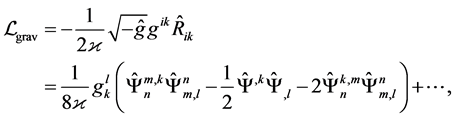 (2)
(2)
where dots denote a full derivative which does not con- tribute to the equations of motion. A variation of the ac- tion of the gravity theory over the normal coordinates leads to the Einstein equation
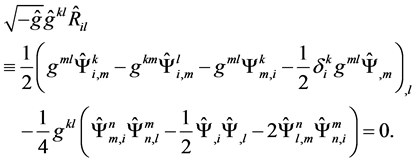 (3)
(3)
The same equations can be rewritten in the form
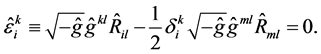 (4)
(4)
In accordance with the general properties of Einstein equations, 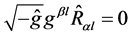 are equations of motion
are equations of motion 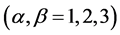 , and
, and 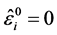 are equations of constraints. Note also the following form in which the Bianci identity can be presented:
are equations of constraints. Note also the following form in which the Bianci identity can be presented:
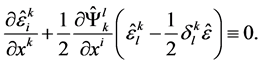 (5)
(5)
2.2. Hamilton Gauge, Conservation Laws and Hamiltonian Formalism
The Hamilton gauge is given by additional conditions
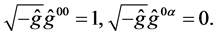 (6)
(6)
In normal coordinates, the conditions (6) are reduced to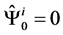 . The specific of the Hamilton gauge is that the Bianchi identity (5) takes the differential form of con- servation laws over the solutions of the equations of mo- tions
. The specific of the Hamilton gauge is that the Bianchi identity (5) takes the differential form of con- servation laws over the solutions of the equations of mo- tions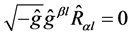 . It reads:
. It reads:
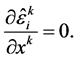 (7)
(7)
After the gauge is applied, the Lagrangian and the equations of motions take the form:
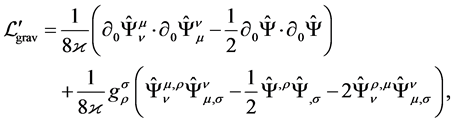 (8)
(8)
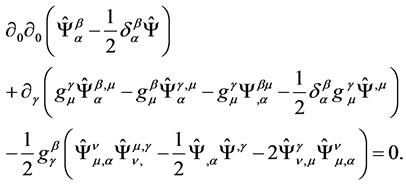
 (9)
(9)
The equations (9) are obtained by variation of the gauged action 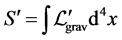 over the variables
over the variables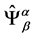 . After the gauge is applied, Lagrangian (8) does not con- tain variables whose variations would produce equations of constraints
. After the gauge is applied, Lagrangian (8) does not con- tain variables whose variations would produce equations of constraints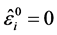 . However, these constraints are re- stored in solutions of the equations of motion (9) by im- position of conditions on the numerical values of inte- grals of motion. As follows from (7), first integrals of the equations of motion (9) are of the form
. However, these constraints are re- stored in solutions of the equations of motion (9) by im- position of conditions on the numerical values of inte- grals of motion. As follows from (7), first integrals of the equations of motion (9) are of the form
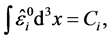 (10)
(10)
where Ci are formally numerical constants whose values are fixed by initial and boundary conditions. The general covariant nature of the equations of constraints imposes the obvious limitations over values of Ci: only those ini- tial and boundary conditions are allowable for the metric in the Hamilton gauge in which constants Ci, appearing in (10), are equal to zero.
Thus, the formalism of the theory, based on a gauged Lagrangian (8), differs from the formalism of non-de- generate field theories only by limitations 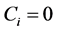 that are related to the initial and boundary conditions but not to the equations. This fact allows to construct the Hamil- ton formalism easily. Generalized momentums are of a standard definition over functional derivatives:
that are related to the initial and boundary conditions but not to the equations. This fact allows to construct the Hamil- ton formalism easily. Generalized momentums are of a standard definition over functional derivatives:
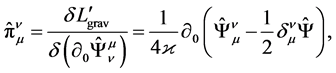 (11)
(11)
where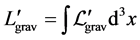 . The gauged action is reduced to the form
. The gauged action is reduced to the form
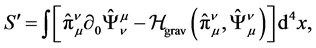 (12)
(12)
where
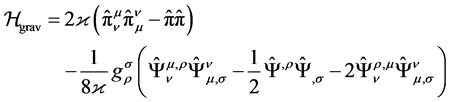 (13)
(13)
is the density of canonical Hamiltonian by which the full Hamiltonian is calculated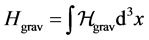 . The varia- tion of action (12) over the generalized coordinates and momentums (as over independent variables) leads to the Hamilton system:
. The varia- tion of action (12) over the generalized coordinates and momentums (as over independent variables) leads to the Hamilton system:
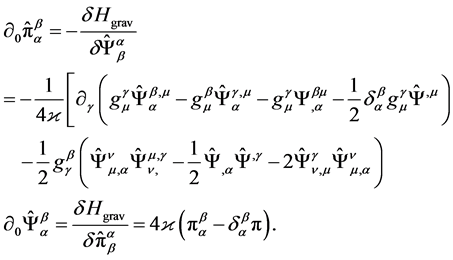 (14)
(14)
As it should be, the Hamilton formalism is mathematically equivalent to the Lagrange formalism, and this can be seen from the fact that the system of Equations (14) is easily reduced to the Lagrange Equations (9). The Hamilton constraint (10) with i = 0, C0 = 0 becomes the formula for calculating of the energy of the gravitational field through surface integral:
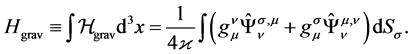 (15)
(15)
2.3. Inertia Fields in Hamilton Gauge
The general formulae for infinitesimal transformations reads
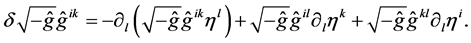 (16)
(16)
For the Hamilton gauge (6), the expression (16) leads to the equations for the parameters of residual transfor- mations:
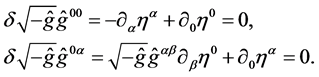 (17)
(17)
The solution of Equations (17) is presented in the form
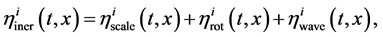 (18)
(18)
where
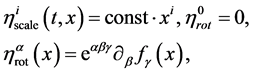 (19)
(19)
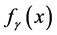 is a function of spatial coordinates defined by ar- bitrarily;
is a function of spatial coordinates defined by ar- bitrarily;
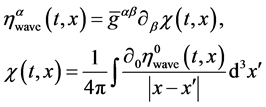 (20)
(20)
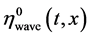 is the solution of the d’Alambert wave equa- tion
is the solution of the d’Alambert wave equa- tion
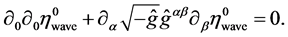 (21)
(21)
Function (18) defines the fields of inertia:
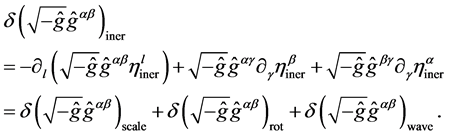 (22)
(22)
According to (19), fields of inertia
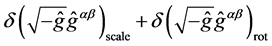
are trivial in the sense that 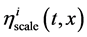 and
and 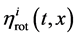 do not interact with gravity. These fields describe the given motions of the reference frame. The motion correspond- ing to a field
do not interact with gravity. These fields describe the given motions of the reference frame. The motion correspond- ing to a field 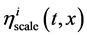 is a given stretch of coordinate grid, and the motion corresponding to a field
is a given stretch of coordinate grid, and the motion corresponding to a field 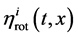 is a given rotation. The lack of connection with the me- tric implies that these fields of inertia do not affect the solution of Einstein’s equations; for this reason they can be excluded from consideration.
is a given rotation. The lack of connection with the me- tric implies that these fields of inertia do not affect the solution of Einstein’s equations; for this reason they can be excluded from consideration.
The function 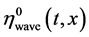 (satisfying the wave Equa- tion (21)) defines a nontrivial field of inertia
(satisfying the wave Equa- tion (21)) defines a nontrivial field of inertia
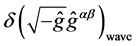 . The nature of this field is following.
. The nature of this field is following.
The condition 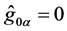 synchronizes the clocks, and component
synchronizes the clocks, and component 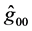 sets the rate of a clock. According to (6), the Hamilton gauge is synchronous, and the rate of a clock is rigidly connected with the dynamics of 3 volumes:
sets the rate of a clock. According to (6), the Hamilton gauge is synchronous, and the rate of a clock is rigidly connected with the dynamics of 3 volumes: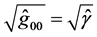 , where
, where 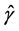 is the determinant of spatial me- tric. Effects of continuous clock adjustment to a new physical situation are reflected in the measured values of 3-dimensional component of the metric in the form of wave field of inertia. It is propagating with the same speed with which a clock located at the point of mea- surement is synchronized with the clocks located at the neighboring points.
is the determinant of spatial me- tric. Effects of continuous clock adjustment to a new physical situation are reflected in the measured values of 3-dimensional component of the metric in the form of wave field of inertia. It is propagating with the same speed with which a clock located at the point of mea- surement is synchronized with the clocks located at the neighboring points.
Note that in the theory of gravity in the Hamilton gauge the non-trivial field of inertia is of one only inde- pendent internal degree of freedom.
3. Path Integral in Canonical Variables and Operator Equations in Heisenberg Representation
The procedure of hamiltonization of classical theory of gravity in the Hamilton gauge is carried out in Section 2.2. Its content and sequence of procedures exactly match to the hamiltonization procedure of Yang-Mills theory [18]. Just as in [18], ch.III, §2, the Hamilton gauge first is introduced in the Lagrangian and the Lagrange equations
of motion, then the theory is presented in the Hamilton form.
Differences between the Yang-Mills theory and the theory of gravity appear during the phase of quantization. According to [19], the fact that in the Yang-Mills theory the Hamilton gauge completely removes the degeneracy, lets go straight to the quantum Yang-Mills theory in the Heisenberg representation by replacing the classical Po- isson brackets with quantum commutators. A transition to a path integral over the canonical variables is of the status of computing the Heisenberg operator of evolution. The completely analogous transition to the quantum the- ory of gravity is not possible because fields of inertia remain in the Hamilton gauge (see Section 2.3). To com- pensate for contributions of interactions of inertia and gravitational fields to the observables, the ghost fields are needed, which occur only in the formalism of path inte- gration. Taking into account this circumstance, the pri- mary postulate (allowing the Heisenberg representation of quantum gravity) is introduced at the path integral level for the canonical variables in the Hamilton gauge:
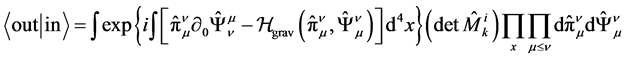 (23)
(23)
where
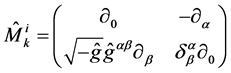 (24)
(24)
is the operator of the system of Equations (17) for the parameters of residual transformations. The expression (23) is obtained from Faddeev’s path integral (see for- mula (5.6) in [11] or formula (24.22) in [12]). It is ob- tained after setting the Hamilton gauge, integration over 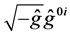 and introduction of normal coordinates and cor- responding momentums. Note that a very simple struc- ture of the gauged action in (23) is due to the fact that in the classical theory in the Hamilton gauge the gauged variables are of the status of Lagrange multipliers to the classical equations of constraints.
and introduction of normal coordinates and cor- responding momentums. Note that a very simple struc- ture of the gauged action in (23) is due to the fact that in the classical theory in the Hamilton gauge the gauged variables are of the status of Lagrange multipliers to the classical equations of constraints.
The computation of the determinant of operator (24) leads to
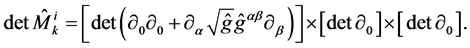 (25)
(25)
The structure (25) completely corresponds to the clas- sification of the fields of inertia in the Hamilton gauge. The localization 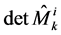 leads to the Lagrangian con- taining only one non-trivial ghost field, which does inter- act with the gravity. The direct localization leads to the path integral over the configuration space of ghost fields:
leads to the Lagrangian con- taining only one non-trivial ghost field, which does inter- act with the gravity. The direct localization leads to the path integral over the configuration space of ghost fields:
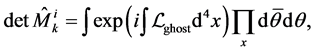 (26)
(26)
where
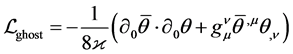 (27)
(27)
is the density of the ghost Lagrangian. A path integral over the phase space is a mathematical equivalent to (26). It reads:
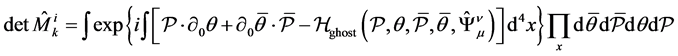 (28)
(28)
where
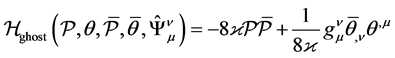 (29)
(29)
is the density of the ghost Hamiltonian. Substitution of (28) to (23) gives a path integral over the extended phase space of gravitational and ghost variables:
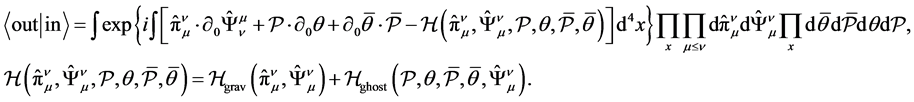 (30)
(30)
Expression (30) is the standard definition of the matrix element of the operator of evolution that defines the dy- namics of state vectors in the Schrödinger representation or, equivalently, the dynamics of operators in the Heisenberg representation. Therefore (30) allows imme- diately writing down the terms of the canonical quantiza-
tion and equations of quantum gravity in the Heisenberg representation.
The graviton sector is:
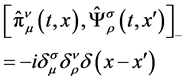 (31)
(31)
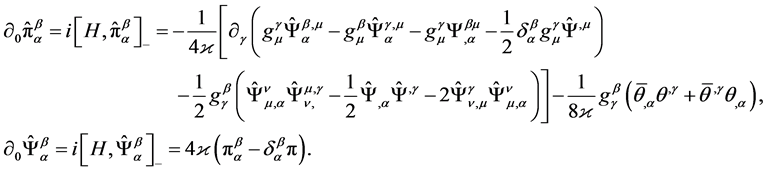 (32)
(32)
The ghost sector is:
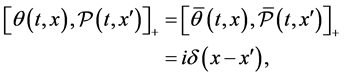 (33)
(33)
 (34)
(34)
In (32), (34)
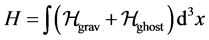 (35)
(35)
is the full canonical Hamiltonian of gravitational and ghost fields. The canonical quantization (31) and (33) and so- lution of operator Equations (32) and (34) are procedures that are of mathematically equivalence to the computa- tion of path integral (30).
It is easy to check that differential conservation laws are satisfied for the solutions of Equations (32) and (34)
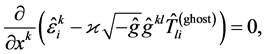 (36)
(36)
where 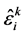 is the density of Einstein tensor,
is the density of Einstein tensor,
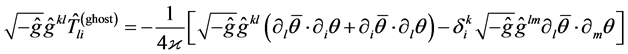 (37)
(37)
is the density of the energy-momentum tensor of the ghosts. Integral conservation laws are presented as con- ditions imposed on the Heisenberg state vector, i.e. on the vector of initial quantum state:
 (38)
(38)
The Hamilton constraint acquires a meaning of the equation for eigenvalues and eigenvectors of the total Hamiltonian of graviton and ghost fields:
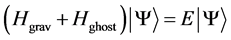 (39)
(39)
A comparison of quantum Einstein’s equations (32) in the Hamilton gauge in the Heisenberg representation with the classical Equations (14) shows that the transition from classical to quantum theory is not limited to the re- placement of C-numeric functions with the operator functions satisfying the canonical commutation relations. In the operator equations of quantum gravity, the opera- tor functions of Faddeev-Popov ghosts automatically ap- pear. They satisfy the canonical anti-commutation rela- tions. The role of ghosts in the Heisenberg equations of motion (32) is exactly the same as in the path integral (30): the ghosts compensate for the effects of interaction of a true gravitational field with a field of inertia. How- ever, in the complete system of Equations (31)-(34) the ghosts formally are of the status of additional dynamic variables, i.e. their status is equal to the status of dyna- mical variable of gravitational field.
At the operator level, the structure of equations of the theory in the Heisenberg representation with canonical quantization of gravitons and ghosts ensures the exis- tence and carrying out routine operations on the transi- tion from (31)-(34) to the representation of interaction, and the construction of S-matrix in the framework of the theory of perturbations. In this theory, gravitons are de- scribed by the deviation of the metric from the metric of Minkowski space. Asymptotic states for gravitons are constructed over the vectors of the Fock space for the quanta of 3D-transverse tensor modes, and asymptotic states for the ghosts are set as vacuum states. Ghosts are present only in the Green function that compensates for
the contribution of the wave field of inertia in the Green function of gravitons. The above S-matrix is identically coincides with S-matrix constructed from the path inte- gral over canonical variables (30) or from the path inte- gral over the Lagrange variables (40). Match of S-ma- trixes constructed in various ways is a direct illustration of the existence of the Heisenberg representation for the quantum theory of gravity in the Hamilton gauge. Appli- cation of this theory to the description of a macroscopic
number of gravitons in the Riemannian space with a self-consistent geometry is discussed in Section 5.
4. Path Integral and Heisenberg Representation in Lagrange Variables
The quantum theory of gravity in the Heisenberg repre- sentation formulated in (31)-(34) is mathematically equi- valent to the calculation of gauged path integral over the Lagrange variables of gravitational and ghost fields:
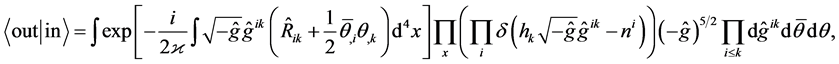 (40)
(40)
where 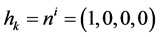 are unit time-like vectors de- fining a Hamilton gauge. Of course, (40) is a specific case of the Faddeev-Popov-DeWitt gauged path integral [14,20,21]. Structurally, (40) is obtained from the gauge in- variant expression
are unit time-like vectors de- fining a Hamilton gauge. Of course, (40) is a specific case of the Faddeev-Popov-DeWitt gauged path integral [14,20,21]. Structurally, (40) is obtained from the gauge in- variant expression
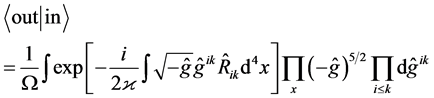 (41)
(41)
through the expansion of unit in the Hamilton gauge and factorization of volume of the gauge group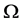 . In the context of existence of the Hamilton formalism, we note that (40) can be regarded as the result of identity trans-
. In the context of existence of the Hamilton formalism, we note that (40) can be regarded as the result of identity trans-
formations of the expression (30). We do not describe these transformations due to their rather obvious.
The expression (40) clearly reflects the unique prop- erty of the Hamilton gauge: the effective Lagrangian of gauged theory is formally defined by the covariant ex- pression
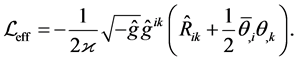 (42)
(42)
Because of this property, the variation of action 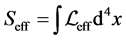 over normal coordinates
over normal coordinates 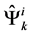 and La- grange variables
and La- grange variables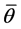 ,
, 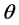 , leads to a system of generally covariant equations for the gravitational and Grassmann scalar fields:
, leads to a system of generally covariant equations for the gravitational and Grassmann scalar fields:
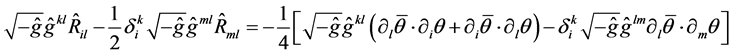 (43)
(43)
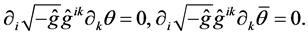 (44)
(44)
The left-hand-side of Einstein’s Equations (43) satis- fies the Bianchi identities, and the energy-momentum tensor of Grassmann fields appearing in the right-hand- side is conservative over the equations of motion (44). The existence of these differential identities allows separating Einstein’s equations to the equations of motion of gravitational field and equations of constraints. It is also clear that after an explicit account of the Hamilton gauge, the gauged equations of motion are reduced to the form (32) and (34). Thus, the Hamilton gauge ensures the ex- istence of Heisenberg representation for the equations of quantum theory of gravity both in Hamilton and in the Lagrange form.
5. Self-Consistent Theory of Gravitons in Macroscopic Riemannian Space
The exact equations in the Heisenberg representation in the Hamilton gauge (32), (34) together with postulates of canonical quantization of (31), (33) claim the status of the theory formulated only on the basis of the first prin- ciples of quantum gravity. We turn to the approximate theory of macroscopic system of gravitons in the macro- scopic space time with the self-consistent geometry. In this theory, the interaction of gravitons with the classical gravitational field is taken into account exactly, and the perturbation theory over the amplitude of quantum fluc- tuations is only used when describing the graviton-gra- viton interaction.
The averaging of normal coordinates over the Heisen- berg state vector in the general case provides non-zero C-numeric function: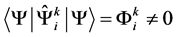 . A quantum fluctuation is defined as the difference between the op- erator and its average value:
. A quantum fluctuation is defined as the difference between the op- erator and its average value: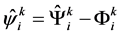 . Substituting
. Substituting 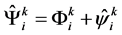 in the formula (1) for the operator of the density of covariant metric gives
in the formula (1) for the operator of the density of covariant metric gives
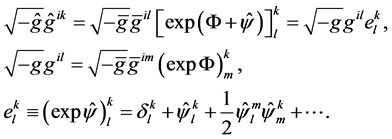 (45)
(45)
A matrix exponential built over C-numeric functions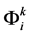 , will be called the density of contravariant metric of the macroscopic space time. In this space, we normally enter the covariant metric
, will be called the density of contravariant metric of the macroscopic space time. In this space, we normally enter the covariant metric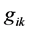 , the connection
, the connection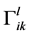 , the curvature
, the curvature 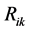 and define covariant derivatives. The quantum fluctuations
and define covariant derivatives. The quantum fluctuations 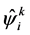 are endowed by the properties of a tensor in the macroscopic space time. The Hamilton gauge
are endowed by the properties of a tensor in the macroscopic space time. The Hamilton gauge 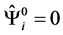 is partitioned into gauge of the macro- scopic metrics and gauge of the quantum field:
is partitioned into gauge of the macro- scopic metrics and gauge of the quantum field:
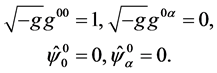 (46)
(46)
Transformations of equations can be made in the Ham- ilton formalism (32), (34) as well as in the Lagrange for- malism (43), (44). To elucidate the general properties of the theory, the Lagrange formalism is more convenient. Substituting (45) in (43) gives:
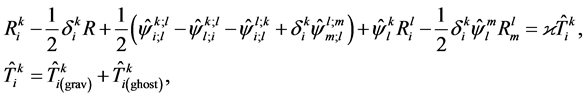 (47)
(47)
where
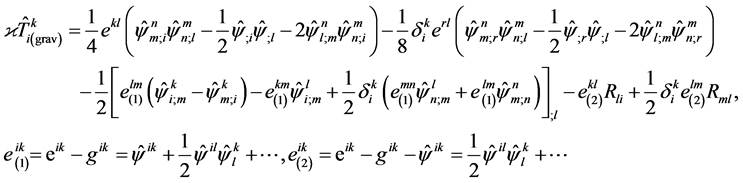 (48)
(48)
is the energy-momentum tensor of gravitons;
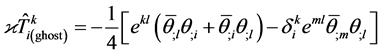 (49)
(49)
is the energy-momentum tensor of ghosts. The Lagrange equations for the ghosts read
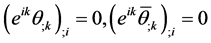 (50)
(50)
Semicolons in (47)-(50) denote covariant derivatives in the macroscopic spacetime.
The transformation of shift 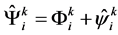 is of physi- cal meaning if the true degree of freedom of the quan- tized gravitational field are contained in the operator function
is of physi- cal meaning if the true degree of freedom of the quan- tized gravitational field are contained in the operator function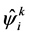 , and the macroscopic gravitational field is self-consistent and serves as a way to describe collective
, and the macroscopic gravitational field is self-consistent and serves as a way to describe collective
interactions in the system consisting of a large (macro- scopic) number of particles. The ability to carry out spe- cific calculations in the approximation of a self-consis- tent field appears when symmetry properties of the ma- croscopic space time allow the introducing of a system of basis state vectors, and on this base to construct a state vector of gravitons and ghosts of a general form. The Einstein equations for the macroscopic geometry are ob- tained from (47) by averaging over the state vector:
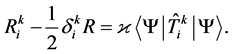 (51)
(51)
The equations for gravitons in the Heisenberg repre- sentation are obtained by subtraction (51) from the exact Equations (47):
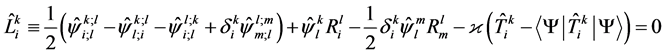 . (52)
. (52)
In terms of the path integral formalism, the existence of Equations (50)-(52), is provided by factorization of the measure of integration and consistent integration, first over the quantum fields of gravitons and ghosts, and then over the classical field. It can be seen from following. After an additive transformation 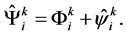 is used, the measure of integration in normal coordinates and Hamilton gauge is represented as:
is used, the measure of integration in normal coordinates and Hamilton gauge is represented as:
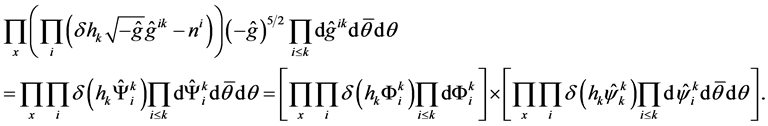 (53)
(53)
Formally, the exact integration of quantum fields ,
,  ,
, 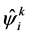 corresponds to the solution of quantum Equa- tions (50) and (52), and the approximate integration of the classical field
corresponds to the solution of quantum Equa- tions (50) and (52), and the approximate integration of the classical field 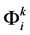 corresponds to the solution of the classical Einstein Equation (51).
corresponds to the solution of the classical Einstein Equation (51).
The system of classical and quantum equations satis- fies three differential identities. The left-hand-side of (51) by definition satisfies the contracted Bianchi identities in the macroscopic space time. In the right-hand-side, the condition for conservation of the expectation value of energy-momentum tensor of ghosts 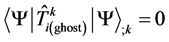 satisfies to the equations of motion for the ghosts (50). The expectation value of energy-momentum tensor of gravitons is of the similar properties. The calculation of a covariant divergence yields:
satisfies to the equations of motion for the ghosts (50). The expectation value of energy-momentum tensor of gravitons is of the similar properties. The calculation of a covariant divergence yields:
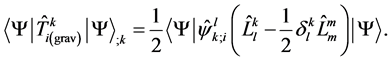 (54)
(54)
As seen from (54), the condition of conservation 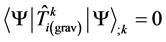 is performed over the quantum equations of motion (52).
is performed over the quantum equations of motion (52).
In the self-consistent theory of gravitons, the non- per- turbative effect of the formation of the geometry of ma- croscopic spacetime is described in semi-classical/semi- quantum level: in the Einstein Equation (51) the source of the classical field is the expectation value of en- ergy-momentum tensor of quantum fields. In the quan- tum sector, the order of a perturbation theory is given by maximum degree “n” in which the operators of quantum fields of gravitons and ghosts are in the quantum equations of motion (52) and (50). In the same order of the perturbation theory, terms of the order of “n + 1” are accounted in the energy-momentum tensor. As seen from (54), the condition of conservativeness of the graviton energy-momentum tensor takes place in each order of perturbation theory separately. This fact is the basis for the application of the perturbation theory.
6. Status of Ghost Fields in the Various Formulations of Quantum Gravity
A specific feature of quantum gravity in the Heisenberg representation is the inevitable presence of ghost fields in the canonical formalism of the theory. Formally (in ma- thematical sense), the ghost sector is a consequence of the lack of gauges fully removing the degeneracy with respect to the residual transformations of the group of diffeomorphisms. Physically, this means that in the the- ory of gravity the fields of inertia are described together with the true gravitational field. In the classical theory of gravity, this does not lead to any problems with interpre- tation because the fields of inertia and gravitational fields are locally separable. Therefore, the deterministic evolu- tion of each of these fields always allows finding invari- ant characteristics of local effects. The specificity of the quantum gravity lies in the fact that because of the lack of gauges completely removing the degeneracy, the ex- isting formalism leads to the quantization of fields of both types (i.e., the uncertainty principle is turned out to be applied not only to the gravitational field but also to the field of inertia).
Of course, in the quantum gravity the question about the status of ghost fields arises as well as the question about the rules of computing the contribution of ghosts to the observables. Answers to these questions are con- tained in the formalism of the theory. The general answer is that in the quantum gravity the ghosts and fields of inertia together form a physical effect. Details of this procedure depend, however, from the specific of a phy- sical problem.
Let’s start with the situation, which is well known and understood. The Faddeev-Popov path integral [10,14] is initially defined as a method of calculating of the transi- tion amplitude between asymptotic states in the frame- work of perturbation theory. Here should be noted that at the very formulation of the problem, the fields of inertia are unobservable in the asymptotic states, which is for- mally provided by appropriate boundary conditions. The impossibility of observing of the inertia fields is auto- matically accompanied by the lack of asymptotic states with the nonzero ghost occupation numbers. Formally, the lack of ghosts is ensured by the stability of the ghost vacuum and by the possibility of conducting of the various “expansions of unit” during the transformations of the gauged path integral. However, the ghosts as well as the fields of inertia are present in the virtual states in the region of interaction, and their quantitative role in the formation of the observable amplitude of the graviton scattering is given by the relevant Feynman diagrams. In various gauges, different inertial and ghost fields are ap- peared but the total contribution of these fields in the graviton sector of S-matrix is gauge invariant.
In quantum gravity in the Heisenberg representation there is a possibility of the task, which physically is fully equivalent to the problem of the S-matrix calculation. Equations (31)-(34) can be used to describe the gravita- tional field whose potentials are only weakly perturb the metric of Minkowski space. In this situation, one can also enter the asymptotic state, and then, specifying the flux of gravitons in the initial asymptotic state to calculate the flux of gravitons in the final asymptotic state. The ghosts together with the inertia fields influence the formation of finite flux of gravitons, and this effect is taken into ac- count in the process of solution of the operator equations of motion.
There are two specifics in the solution of the problem described above. First, the Heisenberg representation in the quantum gravity as well as in the Yang-Mills theory exists only in special gauges, so that the quantum fields of inertia and ghost sector are not arbitrary. Second, in the Equations (31)-(34), there actually are no mathe- matical indications of any special status of ghost fields in contrast to the original path integral where they are. Formally, in these equations, the quantum wave field of ghosts acts as a second dynamic subsystem. Therefore, the exclusion of the ghosts of the asymptotic states is an additional condition. The mathematical consistency of the selection rule of the ghost-free asymptotic states is provided by the stability of the ghost vacuum in the the- ory of perturbations on the background of the Minkowski space.
We now turn to the most non-trivial situation, which is the role of the ghosts in the quantum theory of the gravi- ton macroscopic system. Let us consider the Equations (50)-(52), in the one-loop approximation. In the macro- scopic Einstein equations, the energy-momentum tensors of the gravitons and ghosts are quadratic in quantum fields:
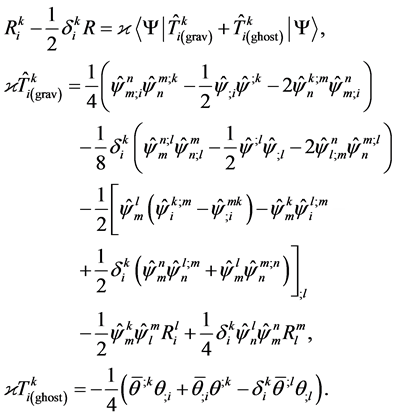 (55)
(55)
The quantum fields of gravitons and ghosts are des- cribed by the following linear equations:
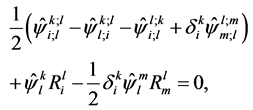 (56)
(56)
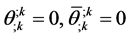 (57)
(57)
As is seen from (55)-(57), the one-loop quantum grav- ity is not confined to the theory of free fields with the spin J = 2 in the curved space time. The objects of the theory are necessarily two fields which are tensor field of spin J = 2 and the scalar Grassmann field with spin J = 0. Moreover, as is seen from the solutions of the equations (55)-(57), the gravitons and ghosts must have an equal status of dynamical subsystems of macroscopic quantum gravity system [1,2]. This somewhat unusual structure of the theory (in comparison with the theory of physical fields with spin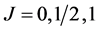 ) needs for additional com- ments.
) needs for additional com- ments.
The first thing that should be stressed is the fact that the inclusion of ghosts in the list of “physical” fields is the result of regular mathematical transformations. These transformations are as follows: the Faddeev path integral over the canonical variables (23) ® equations of quantum gravity in the Heisenberg representation (31)-(34) ® the allocation from the normal coordinates of the gravita- tional field of their mean values and the identity trans- formation of the exact equations in the Heisenberg re- presentation to the self-consistent system of classical and quantum Equations (50)-(52). There is no question about the existence of such transformations because they obvi- ously are in a formal mathematical sense. The question is whether or not these transformations lead to a new physical content of quantum theory of gravity in the last stage of computations (they are initially absent in the gauged path integral)?
The answer to this question is “Yes”. The physical content of the theory is really changed but the reason for this change is absolutely transparent. The source path integral is defined as the mathematical object on the background of Minkowski space with the asymptotic boundary conditions and under the assumption of stabi- lity of graviton (and ghost) vacuum. From a mathemati- cal point of view, the transition from this integral to the theory of the macroscopic quantum gravity system (50)- (52), represents an extrapolation of the theory to a new physical area with the properties that differ from the area in which the theory was formulated initially.
First of all, it should be noted that the formation of the metric of the classical curved spacetime with the self- consistent geometry is a significantly non-perturbative effect of collective interactions in the macroscopic sys- tem. Cosmological applications of quantum gravity make the abandonment of the Minkowski space (appearing in the theory of S-matrix) inevitable in favor of the real ex- isting curved spacetime. Direct consequences of a realis- tic formulation of the problem of describing of a macro- scopic system of massless and conformal noninvariant quantum fields are disappearance of asymptotic states and instability of the graviton-ghost vacuum. Any ob- server located inside such a system (i.e., in fact, inside the real Universe) is in the area of interaction. It is rather obvious that for such an observer the non-perturbative effects of vacuum instability are priority subjects of re- search.
Next, you need to bear in mind that in General Rela- tivity the observer is represented by the fields of inertia which are inevitably quantized (in quantum gravity) in the absence of gauges completely removing the degene- racy. Therefore, in terms of standard quantum gravity, among of locally observable physical quantities, there necessarily are the observables formed by quantum fields of inertia and ghosts jointly. The instability of the va- cuum in the spectral region where the wavelength of quantum fields is comparable to the radius of 4-curvature does not allow to fix the quantum state of these fields by zero occupation numbers. Exactly for this reason, the ghost fields are beginning to perform the role of the se- cond quantum subsystem which is dynamically equal to the graviton subsystem.
Thus, on the one hand, the ghosts perform their stan- dard function in the theory of macroscopic quantum gravity systems, i.e. the ghost contributions together with the contributions of the inertia fields form the observ- ables. But, on the other hand, this function occurs in the non-standard conditions of the absence of asymptotic states and the instability of the vacuum.
This specific of the ghost sector is fully reflected in the equations of one-loop quantum gravity (55)-(57). In these equations, the interaction of gravitons with each other is taken into account through a self-consistent field. According to the most general concepts of the quantum theory of gravity (existing on today), the one-loop effects of the interaction can not be properly described without ghosts. In the Equations (55)-(57), the inertia fields are accumulated in the macroscopic self-consistent field. Therefore, the ghost contribution to the formation of ob- servables is described by the obvious and only a way possible through the influence of ghosts on the self-con- sistent field. This contribution is taken into account through the presence of an averaged energy-momentum tensor of the ghosts in the macroscopic Einstein Equa- tions (55).
The exact solutions of the Equations (55)-(57) de- scribing macroscopic effects of quantum gravity in the homogeneous and isotropic non-stationary Universe are obtained in [1,2]. A possible role of graviton, ghost and instanton condensates in the formation of observable Dark Energy is also discussed in [1,2].
7. Conclusion
In this paper we show that the quantum theory of gravity can be formulated as operator equations in the Hamilton gauge in the Heisenberg representation. The postulate of quantization in this theory is given by canonical commutation and anti-commutation relations for the generalized coordinates and momentums of gravitational and ghost fields. The equations of theory (31)-(34) (or the equa- tions obtained from these Equations (50)-(52)) are used to describe a macroscopic system of gravitons forming a macroscopic spacetime with the self-consistent geome- try.
There is the reason served as one of the main motives in writing this paper. During the last 30 years (since 1977 to 2008) many papers were published on the quantum theory of gravitons taking into account their backreaction on the cosmological background (quantum backreaction theory). To the best of our knowledge, there are no ma- thematically consistent papers correctly taking into ac- count the structure of the existing quantum theory of gravity. In particular, the papers [15,16,22-24] published in Physical Review D are erroneous. The typical errors are following:
1) Use of linear parameterization of the metric fluctua- tions leading to the non-self-consistent system of clas- sical and quantum equations. This is a problem facing the authors of all works on the theory of gravitons, but they tried not to direct attention to the discussion of this mat- ter. Existence of the problem is exhaustively documented in the work [25]. In the same paper it was clearly stated that the use of linear parameterization leads to the need for manual adjustment of the energy-momentum tensor of gravitons. Such a correction, although it restores the conservative nature of the energy-momentum tensor in the background space, is outside of mathematically con- sistent formalism of the theory. In the theory proposed in this paper, the gravitational field undergoes exponential parameterization corresponding to the use of normal co- ordinates in the functional space. With this parameteriza- tion, the energy-momentum tensor of gravitons satisfies the conservative condition automatically (see (54)). The need to use normal coordinates obviously follows from the condition of bringing the path integral to the standard definition of the evolution operator (see (23) and (30)). The same result can be obtained in a purely classical self-consistent theory of gravitational waves. In this case, the consistency of wave and background equations must be ensured by the variational principle. In the frame of this scheme, detailed calculations are given in [2] (Section II.D, formula (II.36), (II.37)).
2) Incorrect gauging (a gauge is imposed not on the full metric but on its fluctuations only). Such a method is a serious and obvious error if it is used in applications in which the macroscopic background has no a global 4- symmetry, permitting the separation of inertia fields. Formally, the mathematical nature of the error is as fol- lows. The group of diffeomorphisms acting in the origi- nal Riemannian space with the metric (1), cannot be fac- torized into the group of diffeomorphisms of the back- ground space and the gauge group of gravitational waves after the separation in this metric of background and wave modes according to (45). However, this error does not affect the erroneous results of [15,16,22-24] because in the quantum theory the main consequence of gauging is the emergence of the ghost sector, which in these works is still ignored.
3) It is an unpardonable error of [15,16,22-24] to com- pletely disregard the most important property of pure quantum gravity (without matter fields) which is its one-loop finiteness. Meanwhile, the one-loop finiteness is a rigorous and well-known T’Hooft and Veltman result [5]. We do not know the reasons why the one-loop fi- niteness is not discussed and simply ignored in [15,16, 22-24]. We can only note that in the self-consistent the- ory of gravitons, incorrect formulations, using the opera- tion of regularization and renormalization of one-loop divergences, have no mathematical meaning. As shown in [2] (Section 12), after introduction of one-loop coun- ter-terms, the initial equation for gravitons is modified, which generates one-loop divergences of the new mathe- matical structure, and so ad infinitum. In other words, the one-loop renormalization of theory of gravitons in those versions of the theory which are used in [15,16,22-24] is simply not possible, and for this reason, these versions do not exist in the mathematical sense. Self-consistent the- ory of gravitons exists only in the form in which it has, according to the T’Hooft and Veltman theorem, the pro- perty of one-loop finiteness.
4) Incorrect use (or ignore) the ghost sector. The lack of a one-loop finiteness in [15,16,22-24] versions of the theory, is mathematically uniquely associated with either ignoring ghost sector [15,16,22-24], or with a mathe- matically incorrect work with this sector [23]. Ignoring ghost sector cannot be justified because in the theory of gravity there are no gauges that completely remove the degeneracy of the metric with respect to non-trivial re- sidual gauge transformations. Apparently, this uncondi- tional and, in general, a trivial fact was just outside the field of attention of the authors of [15,16,22-24]. Some attempt to fix the defect of theory, that is, formally in- troduces the ghosts in a self-consistent theory of gravi- tons, made in [23]. This attempt, however, contains three types of mathematical errors. First, the gauge was ap- plied not to the full metric but just for its graviton part which is mathematically erroneous (see point “2” above). Second, the gauge used in [23] does not provide bringing path integral to the form of the operator of evolution, which makes the transition to the Heisenberg representa- tion impossible. Third, the authors of [23], apparently, to justify ignoring the ghosts in previous works, completely groundless claim that ghosts do not contribute to the ob- servables. For “justification” of this statement, it was drawn the condition BRST invariance of physical states. This third error itself consists of two mistakes. Even in theory of the graviton S-matrix, ghosts participate in the formation of scattering amplitudes, with the status of observables. The condition of BRST invariance refers to the rules of selection of vectors of asymptotic states that are vacuum ones over the occupation numbers of ghosts. In the self-consistent theory of gravitons in the non-sta- tionary universe, there are fundamentally no asymptotic states corresponding to the stable vacuum. Therefore the BRST symmetry provides only a covariance of states but not their invariance. As a consequence, the ghosts are directly involved in the formation of observables. In the self-consistent theory of gravitons, they are geometric characteristics of the background space.
All these works completely lose any meaning after re- normalization of gravitational Lagrangian by quadratic counterterms off the mass shell. This procedure modifies the original definition of the graviton and makes the the- ory mathematically inconsistent. This is an unavoidable and unacceptable internal contradiction of one-loop quantum gravity (see Section 12 of [2].) Because of the finiteness of the theory off the mass shell, the incorrect counterterms simply does not arise with the right algo- rithm of computations. In this paper, we showed that the key to obtaining the correct equations of the one-loop theory (55)-(57) is their correct derivation from the exact equations of quantum gravity. Our point of view is that for the solution of various problems in the quantum grav- ity, the source equations must be the same. Therefore, because of the lack of gauges completely removing de- generacy, the ghosts must be present in any representa- tions of quantum gravity, and they participate in the for- mation of observables starting from the one-loop ap- proximation. In the S-matrix theory, the ghost diagrams participate in the formation of the amplitude of graviton scattering. In the self-consistent theory of gravitons (in the Heisenberg representation) the one-loop interactions are taken into account in the approximation of the self- consistent field. As a result, the ghosts will inevitably take participate in the formation of a self-consistent field via their own energy-momentum tensor on the right- hand-side of the macroscopic Einstein equations self- consistent with the quantum equations of motion. This mathematically inevitable fact was completely ignored in the previously published works.
8. Acknowledgments
We would like to express our deep appreciation to Ludwig D. Faddeev of the Steklov Mathematical Insti- tute for graciously agreeing to read our manuscript and verifying the correctness of our approach before submis- sion to the journal. We are deeply grateful to Mikhail Shifman and Arkady Vainshtein of the University of Minnesota for discussions of the structure and content of the theory. Also, we would like to express our deep ap- preciation to our friend and colleague Walter Sadowski for invaluable advice and help in the preparation of the manuscript.
References
- 1. L. Marochnik, D. Usikov and G. Vereshkov, “Cosmological Acceleration from Virtual Gravitons,” Foundation of Physics, Vol. 38, No. 6, 2008, pp. 546-555. doi:10.1007/s10701-008-9220-6
- 2. L. Marochnik, D. Usikov and G. Vereshkov, “Graviton, Ghost and Instanton Condensation on Horizon Scale of the Universe. Dark Energy as Macroscopic Effect of Quantum Gravity,” arXiv: 0811.4484v2 [gr-qc], 2008, pp. 1-93.
- 3. A. G. Riese, et al., “Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant,” Astronomical Journal, Vol. 116, No. 3, 1998, pp. 1009-1038. doi:10.1086/300499
- 4. S. Perlmutter, et al., “Measurements of Omega and Lambda from 42 High Redshift Supernovae,” Astrophysical Journal, Vol. 517, No. 2, 1999, pp. 565-586. doi:10.1086/307221
- 5. G. T’Hooft and M. Veltman, “One-Loop Divergencies in the Theory of Gravitation,” Annals of Institute Henri Poincare, Vol. 20, No. 1, 1974, pp. 69-94.
- 6. M. H. Goroff and A. Sagnotti, “Quantum Gravity at Two Loops,” Physics Letters B, Vol. 160, No. 1-3, 1985, pp. 81-85.
- 7. P. A. M. Dirac, “The Theory of Gravitation in Hamiltonian Form,” Proceedings Royal Society, Vol. A246, No. 1246, 1958, pp. 333-343.
- 8. P. A. M. Dirac, “Fixation of Coordinates in Hamilton Theory of Gravitation,” Physical Review, Vol. 114, No. 3, 1959, pp. 924-930. doi:10.1103/PhysRev.114.924
- 9. R. Arnowitt, S. Deser and C. W. Misner, “Canonical Variables for General Relativity,” Physical Review, Vol. 117, No. 6, 1960, pp. 1595-1602. doi:10.1103/PhysRev.117.1595
- 10. L. D. Faddeev, “Hamilton Form of the Theory of Gravity,” Proceedings of the V International Conference on Gravitation and Relativity, Tbilisi, 1968, pp. 54-56.
- 11. L. D. Faddeev and V. N. Popov, “Covariant Quantization of the Gravitational Field,” Soviet Physics—Uspekhi, Vol. 16, No. 6, 1974, pp. 777-789. doi:10.1070/PU1974v016n06ABEH004089
- 12. N. P. Konopleva, V. N. Popov and N. M. Queen, “Gauge Fields,” Harwood Academic Publishers, Amsterdam, 1981.
- 13. R. P. Feymann, “Quantum Theory of Gravittation,” Acta Physics Polonica, Vol. 24, No. 6, 1963, pp. 697-722.
- 14. L. D. Faddeev and V. N. Popov, “Feynman Diagrams for the Yang-Mills Field,” Physics Letters B, Vol. 25, No. 1, 1967, pp. 29-30. doi:10.1016/0370-2693(67)90067-6
- 15. L. H. Ford and L. Parker, “Quantized Gravitational Wave Perturbations in Robertson-Walker Universes,” Physical Review D, Vol. 16, No. 6, 1977, pp. 1601-1608. doi:10.1103/PhysRevD.16.1601
- 16. F. Finelli, G. Marozzi, G. P. Vacca and G. Venturi, “Adiabatic Regularization of the Graviton Stress-Energy Tensor in de Sitter Space-Time,” Physical Review D, Vol. 71, No. 2, 2005, 5 p. doi:10.1103/PhysRevD.71.023522
- 17. L. D. Faddeev, “Feynman Integral for Singular Lagrangians,” Theoretical and Mathematical Physics, Vol. 1, No. 1, 1969, pp. 1-13. doi:10.1007/BF01028566
- 18. A. B. Borisov and V. I. Ogievetsky, “Theory of Dynamical Affine and Conformal Symmetries as Gravity Theory,” Theoretical and Mathematical Physics, Vol. 21, No. 3, 1975, pp. 1179-1188. doi:10.1007/BF01038096
- 19. L. D. Faddeev and A. A. Slavnov, “Gauge Fields. Introduction to Quantum Theory,” 2nd Edition, Addison-Wesley Publishing Company, Boston, 1991.
- 20. B. S. DeWitt, “Quantum Theory of Gravity. I. The Canonical Theory,” Physical Review, Vol. 160, No. 5, 1967, pp. 1113-1148.
- 21. B. S. DeWitt, “Quantum Theory of Gravity. II. The Manifestly Covariant Theory,” Physical Review, Vol. 162, No. 5, 1967, pp. 1195-1239. http://dx.doi.org/10.1103/PhysRev.162.1195
- 22. L. H. Ford, “Quantum Instability of De Sitter Space-Time,” Physical Review D, Vol. 31, No. 4, 1985, pp. 710-717. doi:10.1103/PhysRevD.31.710
- 23. J. Garriga and T. Tanaka, “Can Infrared Gravitons Screen Lambda?” Physical Review D, Vol. 77, No. 2, 2008, 9 p. doi:10.1103/PhysRevD.77.024021
- 24. N. C. Tsamis and R. P. Woodard, “Reply to ‘Can Infrared Gravitons Screen Lambda?’” Physical Review D, Vol. 78, No. 2, 2008, 7 p. doi:10.1103/PhysRevD.78.028501
- 25. L. R. W. Abramo, R. H. Brandenberger and V. F. Mukhanov, “Energy-Momentum Tensor for Cosmological Perturbations,” Physical Review D, Vol. 56, No. 6, 1997, pp. 3248-3257. doi:10.1103/PhysRevD.56.3248

