Journal of Modern Physics
Vol.3 No.11(2012), Article ID:24876,11 pages DOI:10.4236/jmp.2012.311227
Universe, Dark Energy and Dark Matter
Protvino, Moscow, Russia
Email: konushko@mail.ru
Received August 13, 2012; revised September 16, 2012; accepted September 23, 2012
Keywords: Expansion of the Universe; Dark Energy; Dark Matter
ABSTRACT
The investigations into the structure of the gravitation field formed by stars, galaxies and their clusters have allowed an alternative explanation for the effect of red shift in stellar spectra; they also have “stopped” the expansion of the Universe and disregarded “dark” energy (DE). The characteristic features of the structure of gravitational field for large galaxies give a clear indication of the mysterious “dark” matter (DM) which enables eliminating it in the Universe. And, finally, the theory of granular space may prove the existence of the Universe as a unique one.
1. Introduction
Far—removed star systems—galaxies and their clusters are the best-known structural units of the Universe. They can be observed at huge distances and the studies into their motion have formed a basis for investigating the kinematics of the Universe. What can we find observing far-removed galaxies? Figure 1 shows the relationship between the red shift of spectral lines and the stellar magnitude of the brightest galaxies in their clusters [1].
Strictly speaking, our instruments show that the farther is the galaxy, the greater is the red shift of its spectral lines. At present red shifts are expressed by equivalent velocities. An object removing from us in normal Euclidean space would have the same red shift. Equivalent velocity means a velocity which such an object must have in order to have a red shift with its magnitude observed.
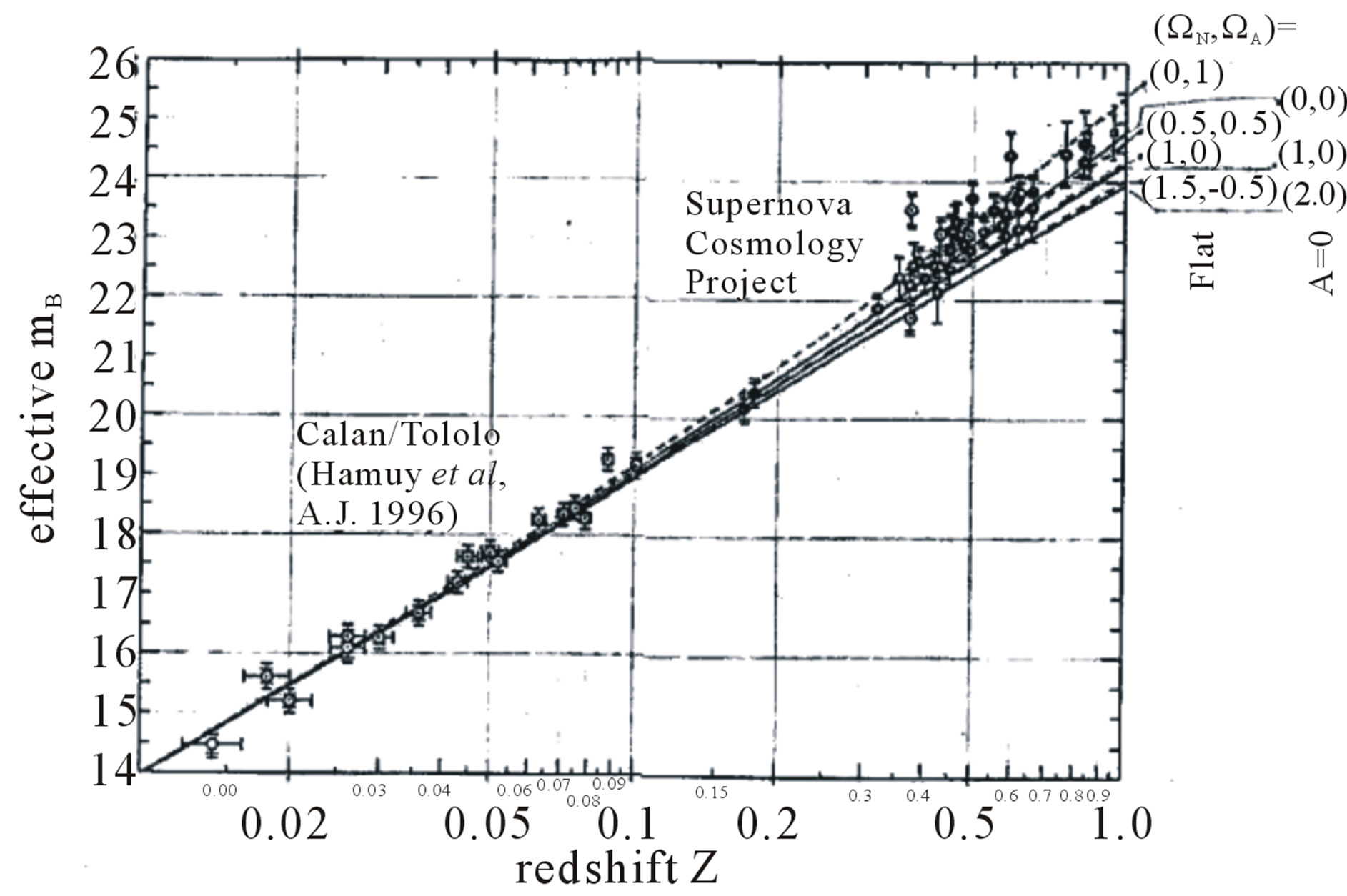
Figure 1. The analysis of data on the supernova 1a explosions.
In 1914 V. Slipher explained this red shift of spectral lines by the removal of galaxies from us. E. Hubble developed criteria for distance measurements based on the characteristics of individual stars inside galaxies. By 1929 he had got reliable results for 18 galaxies. A correlation of these distances with beam velocities showed a distinct linear dependence of velocity on distance which is called by right as the Hubble law.
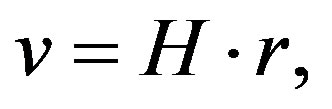
where ν is the velocity, r is the distance and H is the Hubble constant.
In 1922, however, A. Fridman while, solving Einstein equations, arrived at the conclusion on Universe expansion.
A very important feature of distribution of galaxies around us is that it is homogeneous and isotropic. The conclusion is as if galaxies were arranged uniformly around as and this uniformity applies not only to their distribution but also to the law of increase of their velocities as they move away from us. How can it be explained? It may be suggested that man takes the central position in the Universe and all the galaxies are running away from us. Other scientists state that the Universe is uniform by structure and all the points in it are equal. In this case the Universe would be isotropic when observed from any galaxy where man might live. This interpretation correlates with observations.
Galaxies assembled together as groups and clusters of different scales form a cellular-net structure of the Universe. The size of empty regions where there are very few galaxies or no galaxies at all is about 30 to 40 Mpc. the distances between the largest super clusters of galaxies placed in the nodes of the cellular-net structure may range from 100 to 300 Mpc. The most of luminous matter in the form of galaxies and their clusters is distributed almost uniformly.
2. The Nature of Red Shift
As said in Introduction, A. Fridman used Einstein equations to construct a model of the Universe. But many years later it was found out that there was no need to use tensor calculus, the most complicated body of mathematics, to construct the mechanics of mass motion in a uniform Universe. This was proved in 1934 by E. A. Milne and W. H. McCrea. This wonderful possibility is caused by the following thing. A spherically-symmetrical material shell cannot produce any gravitational field in the whole inner cavity and the space-time must be flat.
The Universe does not contain such huge spherical regions but we can imagine them by “scooping” out all the galaxies out of a big (~300 Mpc) spherical volume and then bringing them back, one after another, into the resultant cavity with fiat space-time. When bringing back the galaxies we can express their gravitational interacttions by Newton’s laws of gravitation as attraction between individual galaxies in our spherical cavity. Such an approach to the galaxies inside an imaginary spherical cavity which interact with each other by the law of gravitation but not with the matter beyond this region enables us to describe the dynamics on the boundary of this region.
Imagine a big spherical volume of space and yourself in its centre. The radius of this sphere must be small as compared with the dimension of “visible world” but large enough for a lot of galaxies to be place in it. A galaxy inside this region, close to the surface of the sphere, is acted upon by gravity forces directed towards its centre as if the whole matter was accumulated in it. In this case the gravity potential on the surface of this sphere φ:
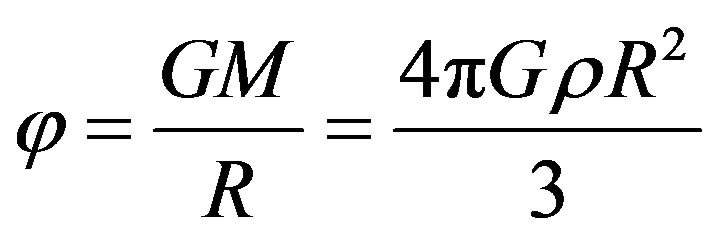 where M is the mass contained in the sphere, R is the radius of the sphere, ρ is the mean density of matter in the Universe, G is the gravity constant. But the potential φ = υ2, where υ denotes the velocity that can be obtained by any body falling on the surface of this sphere from an infinitely large distance. At this instant the same body would have the acceleration a:
where M is the mass contained in the sphere, R is the radius of the sphere, ρ is the mean density of matter in the Universe, G is the gravity constant. But the potential φ = υ2, where υ denotes the velocity that can be obtained by any body falling on the surface of this sphere from an infinitely large distance. At this instant the same body would have the acceleration a:
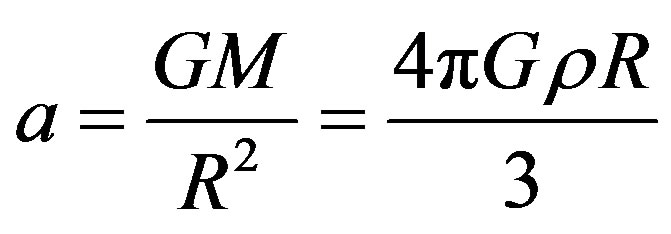 Then
Then
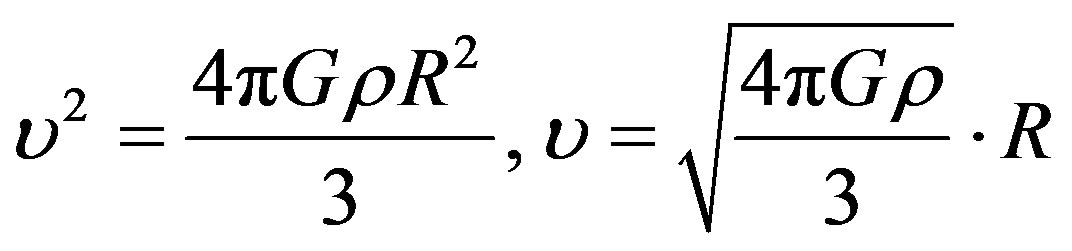
 ,
,
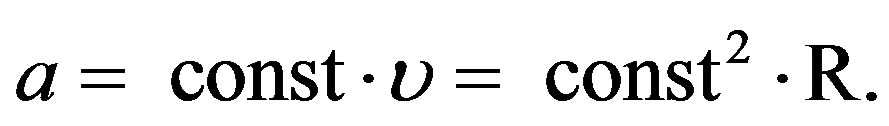
In this traditional interpretation there is not a word about the expansion of the Universe, let alone accelerated expansion. In model cosmology, however, the physical meaning of velocity υ and a characterize the expansion of the Universe with its acceleration determined by the mass M enclosed in a sphere with its radius R.
As said in introduction, the hypothesis adopted in cosmology and astronomy is that the red shift of galaxies is caused by their mutual repulsion. In more detail it means that the scattering of galaxies results in a red shift of their radiation caused by the Doppler Effect. The red shift z is related to the velocity of removal υ as
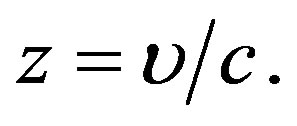
This relation is valid for not very big velocities υ when z < 1.
The magnitude z is defined in a different wary
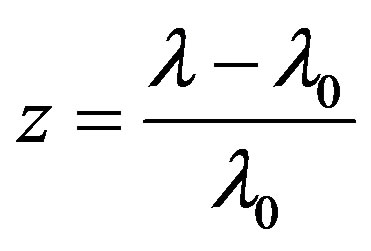 where λ0 is the standard wavelength, λ is the shifted wavelength. This shift is really red when the value of z is positive. When z is negative, this means a shift towards the blue range of spectrum.
where λ0 is the standard wavelength, λ is the shifted wavelength. This shift is really red when the value of z is positive. When z is negative, this means a shift towards the blue range of spectrum.
As a photon moves in a uniform gravitational field characterized by acceleration of gravity force g over the distance l in a direction opposite to that of mg, its energy must decrease by mgl = ћωgl/c2 since, according to the so-called principle of equivalence, the photon has a gravitating mass equal to its inertial mass m = ћω/c2.
Consequently, the photon energy will be
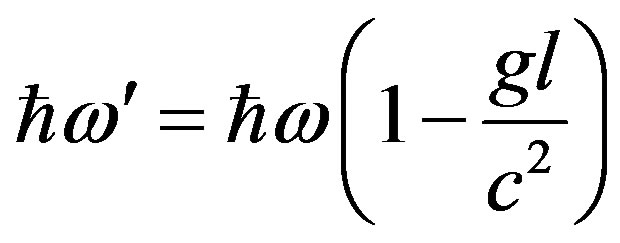 whence it follows that the photon frequency has the value
whence it follows that the photon frequency has the value
 .
.
By the last formula, the relative change in photon frequency

is in proportion with the change in gravity potential
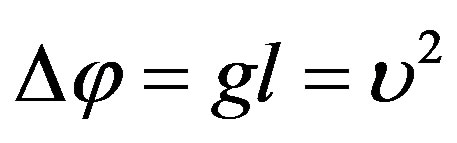 where v is the characteristic of a gravity field on the surface of a star. If z < 1, the change of frequency Δω/ω differs greatly from the value given by Doppler effect.
where v is the characteristic of a gravity field on the surface of a star. If z < 1, the change of frequency Δω/ω differs greatly from the value given by Doppler effect.
Hence, a gravitational red shift cannot be used to explain the Hubble effect and the cosmological red shift has been closely related to the scattering of galaxies (the expansion of the Universe).
So far nobody has paid attention to the colossal difference between the gravity potential of an individual massive body φstar and the gravitate potential of our imaginary ball φball. For clarity, let us compare them:
 ,
,
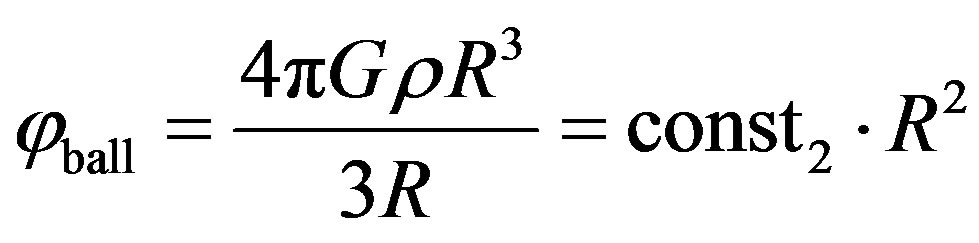 .
.
For one and the same R a change in φstar by 10 times will cause φball to be changed by 100 times! So, the relationship between these potentials is square-law.
Since, for illustration, υ/c < 1, us a photon runs away from a star at the distance R, the red shift zstar = υ2/c2, whereas a photon emitted from the surface of a ball towards the observer is subjected to a red shift due to square-low dependence
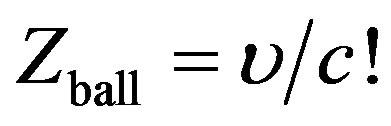
Let us prove this evidence by treating the Doppler’s effect in the context of granular space theory. When a particle moves in space, a definite amount of excess matter carried by kinetic energy deforms space cells. This deformation affects cells at a depth equal to the particle wavelength.
If a partied emits a photon in the direction of its motion, the latter moves for a while over space cells overloaded with kinetic energy matter thus increasing its energy, that is, the frequency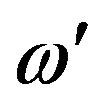 .
.
In its turn, in a gravitational field, too, the space cells are filled with the matter formed when elementary particles are born. The structure of various physical fields and their formation are comprehensively studied in our articles [2-7].
It is the excessive matter of space cells that is responsible for the change of frequency as the photon moves in a gravitational field. This is our answer to L. Brillouin’s puzzling question “How can it occur? We want frankly to say that we do not know how to explain it. We have to accept it as quite an incomprehensible experimental fact.”
Assume that a is the particle size and b is the distance at which the photon breaks away from the particle. What is b equal to in this case? This is the distance covered by the particle within the time
 .
.
With the velocity of the particle υ, the covered distance will be
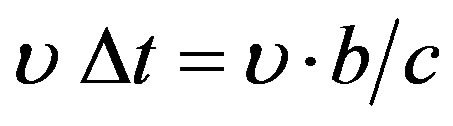 .
.
But b means the distance plus a
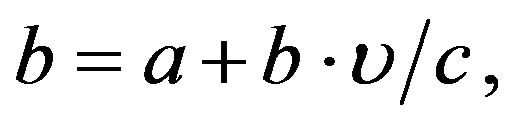
hence,
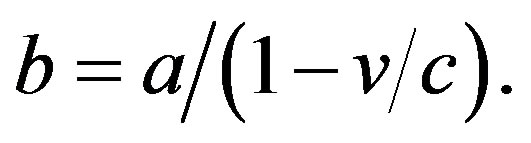
The ratio b/a shows by how many times the photon can increase its energy
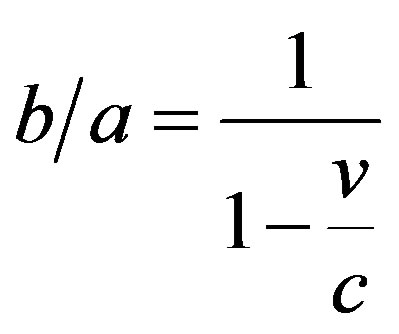 or
or
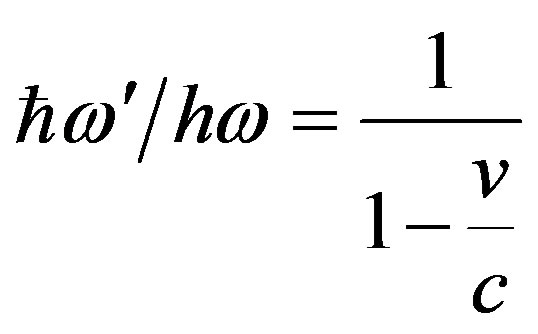 .
.
Allowances must be made for the retardation of all the natural processes in a moving reference system—the well-known radical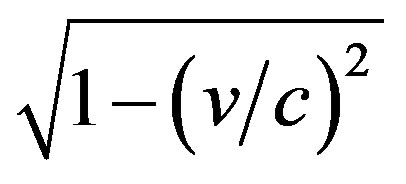 . The formula for red shift can be obtained by changing the sign of velocity
. The formula for red shift can be obtained by changing the sign of velocity
 or taking into account that
or taking into account that , we have
, we have
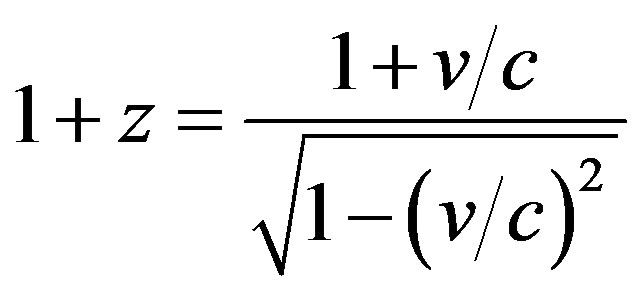 .
.
If a particle emits a photon in the opposite direction of its motion, the photon moves for a while over space cells whose deformation gradient is opposite to the photon motion and the photon has to give part of its energy (mass) to the moving particle. In this case the red shift effect can be observed.
For further consideration of the Doppler’s effect the governing factor is the statement of granular space theory that velocity is a degree of elementary cell deformation and is, to a greater extent, typical of rest rather then motion.
For our case the following factor is important. While the photon is moving with the particle, the deformation of space cells is characterized by the velocity υ; when it breaks away from the particle the photon enters cells with zero deformation υ → 0.
Let us turn again to the sphere under consideration with its radius R. The potential φ of the gravitational field set up by the whole matter inside the sphere will be φ = υ2 on its surface. The photon emitted by an electron on the boundary of the sphere and belonging to a galaxy will move for a while towards the observer at the point O in space where the cells are deformed in the same way as they are deformed by the kinetic energy of a particle moving with the velocity υ. The potential of the observer at the point O is equal to zero. Hence, the photon will lose its energy just as it lost it while breaking away from the moving particle. Here we have the full analogy of the Doppler effect.
Thus, space itself played an angry trick on scientists which later resulted in a fatal error in studying the expansion of the Universe: the space potential simulates the Doppler Effect.
Dozens of physical phenomena considered in [2-7] are decisive evidence that the velocity υ characterizes the deformation of space cells and the acceleration a defines the gradient of this deformation. It is just this gradient that terminated in false representation of the expansion of the Universe. The dark energy hypothesis has been put forward just to correlate somehow theory and the paradoxes results of supernova outburst observations.
Two hundred years ago W. Leibniz came up with a very simple and profound idea that “theory mast be simpler than the data which it explains, otherwise it does not explain anything. The conception of a scientific law makes no sense if it allows an unlimited level of mathematical complexity…”
The granular space theory releases experimentalists from searching for dark energy (quintessence) because it does not exist in the Universe.
3. Hubble-Sandage Paradox
According to the granular space theory, the only building element of the Universe is an elementary cell with its size [2-7].
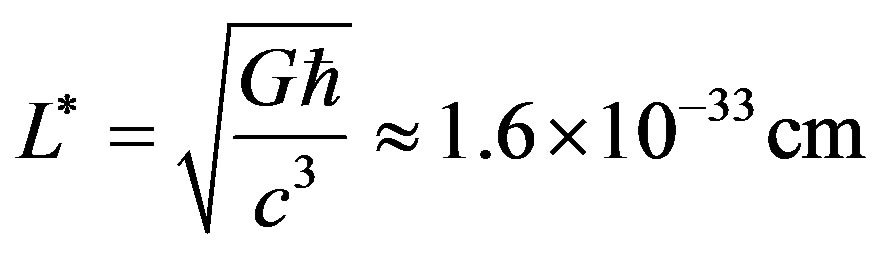 .
.
From this it follows that space is uniform and isotropic. If we mentally separate some regions of size 300 Mpc in a certain volume of the Universe and count the number of galaxies in each of them, it will be almost the same for all the regions. The same result will be obtained in case of clusters and super clusters. A volume with its cross size of 300 Mpc, starting from which the space distribution of galaxies is approximately uniform, is called a uniformity cell in the Universe. In the nearest region, however, in the volume observed by Hubble the distribution of matter is not uniform at all. On the contrary, the galaxies are distributed here unevenly forming with their size of about 1 Mpc.
Using the orthodox theory of Universe expansion we can ask the question: how a regular velocity of expansion can correspond to the law of velocity-distance proportionality υ = H·R under such conditions. According to Fridman theory, this law is only valid in case of homogeneous distribution of matter in space.
The scattering of galaxies looks as though a global cosmological flow began directly near us and running on almost up to the Universe horizon retained its kinematic identity. But how can it be?
This is the paradox existing since Hubble. In 1999, 70 years after his discovery, Allan Sandage wrote that “we still remain with this mystery”.
The latest information on galaxies moving in a region of extremely small galaxy scales has been obtained by I. D. Karachenzev et al. [8]: Hubble constant H ≈ 72 km/s per Mpc. According to Sandage’s group, H ≈ 64 km/s per Mpc.
A fundamental conclusion of the granular space theory, however, is that v2/c2 means the relative deformation of space cells and the acceleration a is the gradient of this deformation.
It is shown above how the behavior of the gravity potential on the boundary of a ball with its radius R φball = const2·R2, rather than φstar = const1/R, fully simulates the Doppler effect and the radiation of a star on the boundary of a ball results in a red shift in the centre of observation:
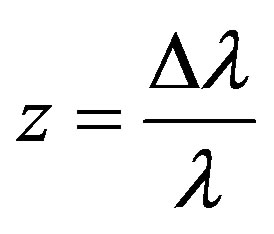 .
.
With velocities over 50,000 km/s, the following formula should be used:
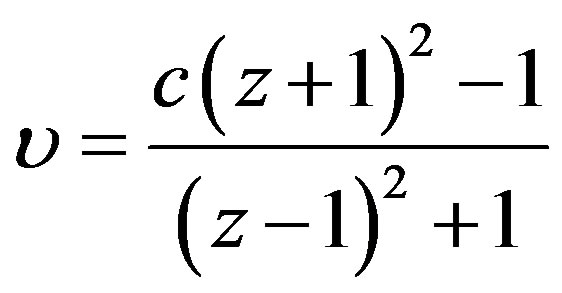 .
.
This correction does not change our fundamental conclusion on the physical meaning of the imaginary Doppler Effect since υ/c < 1 as before.
Consequently, it should be said again that there is neither expansion, nor accelerated expansion and no dark energy in the Universe.
For good reason, of most interest is the fact that the regular Hubble law of galaxy scattering holds true in our nearest galaxy environment at distance just of several Mpc.
About 40 years ago the autor found out that deformation of elementary cells predominates in the Universe: radial and spiral. It is due to deformation that we can establish whether the distribution of matter homogeneous and isotropic.
This fact reveals Sandage’s mystery: even though we consider distances not 1.5 Mpc but one thousand times less or even much less, peculiar star velocities disregarded, Hubble’s law would be fulfilled strictly because it is determined by the gravity potential (escape velocity) on the surface of our imaginary ball R.
Let us consider the following example.
It is known that the mass of a local group of galaxies is 1.5 × 1012 solar masses and the distance to the observer R ≈ 1.5 Mpc. It this case the escape velocity of this group
 According to Hubble’s law
According to Hubble’s law
 .
.
As it can be seen, the Hubble constant only characterizes the structure of space rather than the Universe, expansion. This value of H is in complete agreement with experiment.
This constant shows that its mean value does not depend either on the direction towards the galaxy or on the distances in the galaxy world. The cause of this constancy is evident: it characterizes uniform and isotropic deformation of space cells of the Universe.
4. “Latent” Masses
Our Universe is full of mysteries. One of them is related to “latent” masses. A lot of big galaxies have several small galaxies, that is, their satellites. They turn round the central galaxy, and analysis of their motions enables estimating the masses of big galaxies. If the central galaxy is entirety inside the orbits of its satellites, the gravity forces acting upon all these satellites are conditioned by one and the same gravitating mass. The rotation velocity is determined by Newton’s law and decreases with radius.
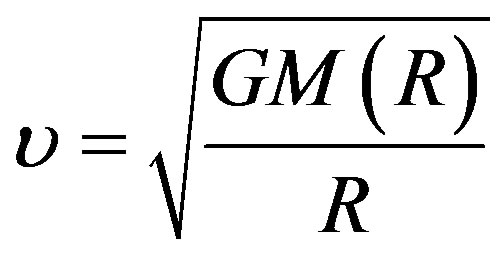 . (1)
. (1)
It has been found recently that the law (1) is not fulfilled for groups of satellites of our Galaxy, Andromeda nebula and some other galaxies. Every time the velocities of the satellites at distances of up to ten radii of the galxy were measured, the result was that they do not decrease with radius but remain (with a know accuracy) constant. This fact is proved by a dashed line on the rotation curve (Figure 2). The violation of this law (1) in the motions of galaxies-satellites gave birth to the hypothesis that the mass of the central galaxy is actually not limited by the
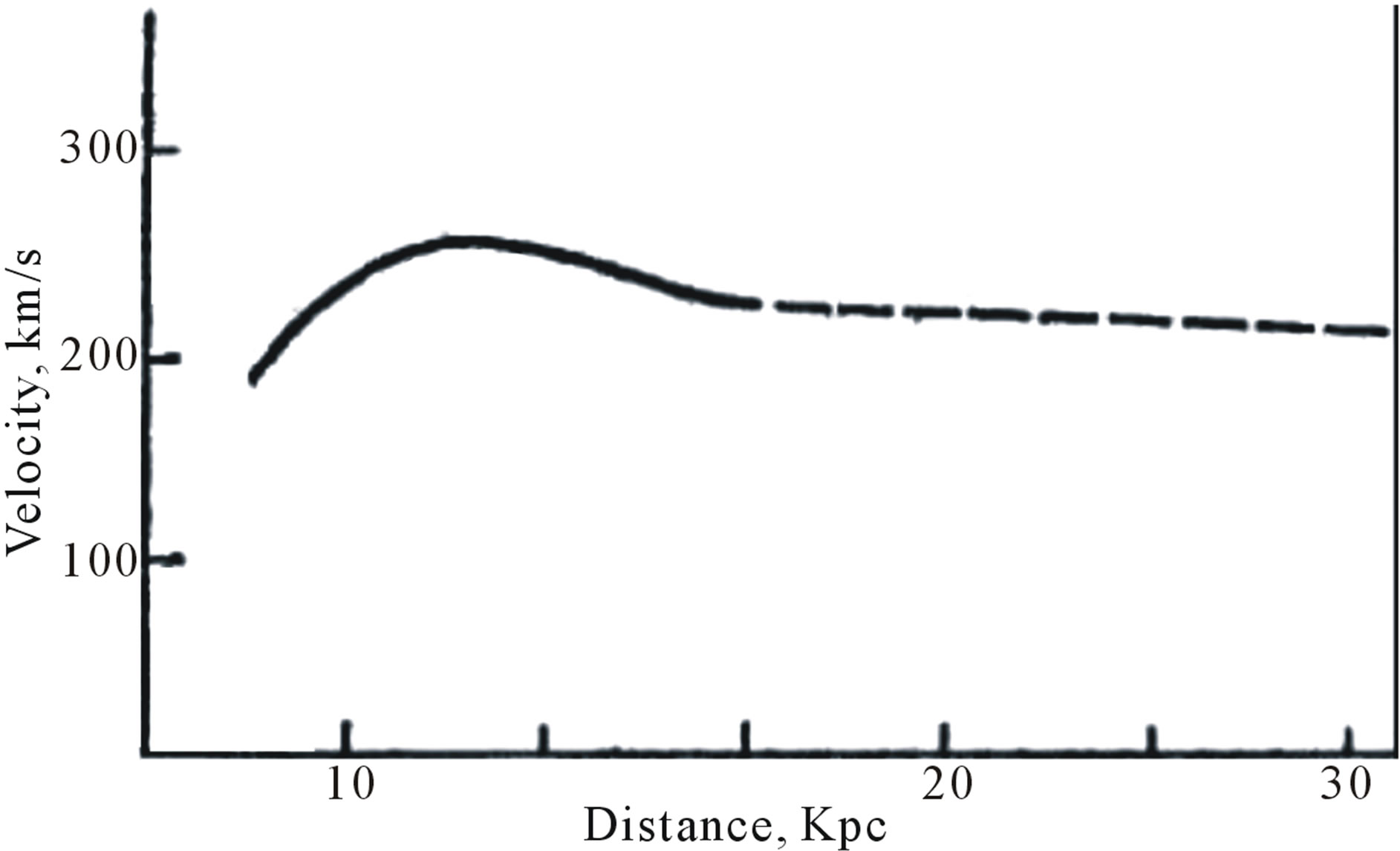
Figure 2. The dependence of the linear rotation velocity of galaxies on the distance to the centre (rotation curve). The dash line is the coronal region.
one lying within the volume seen in the photo but is distributed throughout a much bigger volume.
Contrary to stars, this additional mass does not emit light, it is invisible but sets up a considerable gravity force, in addition to the stellar gravity force.
Thus the term of “latent” masses (dark energy) around galaxies was introduced.
Latent masses are selective by nature: they form an extent galaxy corona, that is, exist beyond the galaxy, so galaxy-satellites move not in a vacuum but among invisible gravitating masses.
The gravity force acting on satellites and being responsible for their dynamics is made up of the mass of visible forces and the latent mass inside the satellite orbit.
The rotation curves similar to the one shown in Figure 2 are plotted for a considerable number of big galaxies and all of them have an extent outer region where the rotation velocity remains more or lets constant. The corona of our Galaxy extends, at least, up to 60 Kpc and, maybe, up to 100 Kpc Its mass may be as great as ~1012 M (solar). It should be noted that the radius of Galaxy disk Rd ~ 15 Mpc and the mass ~1011 M (solar).
The density of latent masses (their gravitational action) decreases from the centre to the outside and at rather a long distance it drops more and more and is reduced to zero.
Latent masses also manifest themselves in the dynamics of galaxy groups and clusters. They seem to be accumulated mainly around the most massive galaxies of a cluster thus forming their coronas.
So, from the aforesaid it might be said that the behavior of latent masses is rather unexpected. They “love” only big galaxies and are grouped beyond galaxies rather than inside them. Their influence drops quickly as satellites move away from galaxies and, finally, they only manifest themselves as gravitation.
These quite incompatible features make us reject the “dark matter” hypothesis and look for a more realistic cause of the constancy of satellite velocities in the galaxy corona. The key this mystery is the form of big galaxies (Figure 3).
The thickness of the Galaxy disk is 45 times less than its radius.
Besides, the galaxy nucleus is shaped like an ellipsoid of revolution with its semi-major axis being three times

Figure 3. The diagram of Galaxy. (light years).
as great as the semi-minor axis which increases its analogy with a cylinder.
Andromeda nebula and other galaxies have similar structures. If we observe such galaxies from an edge, we can see just a wide band or a cylinder in section. This is rather a rough analogy but only it can solve our task since both the size of galaxies and the velocities of satellites are roughly estimated, too.
Now we consider the galaxy gravity field and calculate the flow Φ of intensity vector of this field E through the closed surface S which encloses the galaxy mass M:
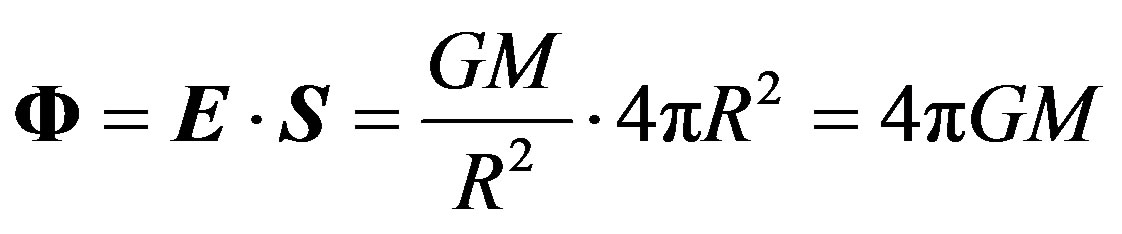 (2)
(2)
By analogy with electrostatics, the Gauss theorem for a gravity field can be written thus: the intensity vector flow of a gravity field through a closed surface is equal to the sum of gravity charges enclosed inside this surface multiplied by 4πG.
Let λ be the linear density of galaxy mass: λ = M/2R, where M is the galaxy mass, R is its radius.
Imagine a closed cylindrical surface with r and h coaxial with our imaginary band (galaxy). The vector flow E through the surface under study is:
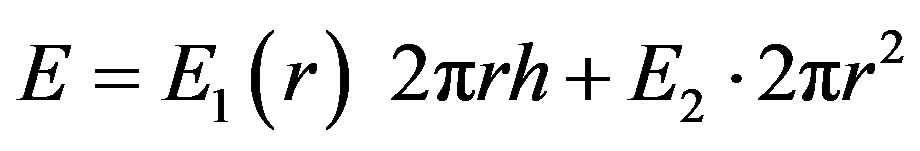
If r > RG the gravity charge inside will be m = λ·h, h = 2R, m = M.
Using the Gauss theorem we have
 (3)
(3)
with 
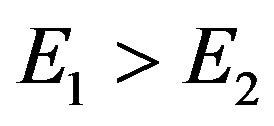 , and the second term in (3) can be disregarded taking into account the inexact experimental cosmological data and our rough approximation.
, and the second term in (3) can be disregarded taking into account the inexact experimental cosmological data and our rough approximation.
Hence,
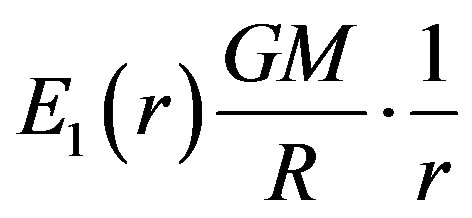
when the gravity force acting on a satellite m is centrifugal
 we have
we have
 (4)
(4)
This stunning result makes us part, at last, with “dark matter” like we have already parted with “dark energy”.
The mathematics just considered by us can only be applied to satellites rotating in the same plane with the galaxy. Such satellites make up the bulk of them.
Though stars and nebulas within spiral galaxies move in a continuous way, they take part first and foremost in the rotation of galaxies around the axis perpendicular to its equatorial plane. Thus, an observer on one of such stars at the galaxy edge would see it in the same way as we can see the Milky Way, in the form of a whitish luminous band.
At the distance 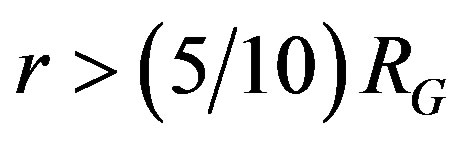 from a galaxy the analogy with a cylinder dies away quickly, that is why the former “dark matter” disappeared too and satellite velocities were not constant any longer. Now it is already quite clear why this matter “close” mainly big galaxies and “hid itself” beyond galaxies in their corona because the gravity field inside a galaxy is quite different in shape.
from a galaxy the analogy with a cylinder dies away quickly, that is why the former “dark matter” disappeared too and satellite velocities were not constant any longer. Now it is already quite clear why this matter “close” mainly big galaxies and “hid itself” beyond galaxies in their corona because the gravity field inside a galaxy is quite different in shape.
We must be grateful to C. Gauss and S. D. Poisson for developing the potential theory in the 19th century since it helps us to get insight a huge number of natural phenomena and separate reality from mysticism. On largescale sky maps galaxy clusters often show up as alongated chains which remind of cylindrical surfaces more than galaxies. If the masses of galaxies are not large 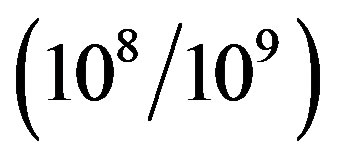 Ms, the analogy with a cylinder does not work, and they have not “latent masses”.
Ms, the analogy with a cylinder does not work, and they have not “latent masses”.
5. Homogeneity and Isotropy of Universe
There is another mystery. For example, a difference between star clusters forming galaxies and galaxy clusters. In the fist case the distances between star are huge, ΔRs ~ 1018 cm, as compared to the sizes of stars (the size of an average star, the sun for example, R€~ 1011 cm), when as the mean distances between galaxies in galaxy clusters just 10 to 20 times less than their sires. Why is it so? It is also strange that all galaxies with maximum luminosity are probably more or less alike. Galaxies can obviously reach only a certain size and never exceed this limit. Why? Why must there be an unknown upper limit to the mass and luminosity of galaxies?
Galaxies have a great variety of shapes. On the contrary, the sizes of galaxies turn out, as a rule, to be almost alike. In any case for the basic classes of galaxies the size is a more constant parameter than their shape, mass or luminosity.
It is common knowledge that a thermodynamically non equilibrium system develops ordered structures which have been the subject of synergёticós. The author of [2-7] has been studying in succession physical phenomena assuming that both material space and the whole Universe are only made of one element, a three-dimensional elementary cell, the value of which was found by M. Plank in 1900 , and the size of an elementary cell is determined by the Compton length λ = ћ/mc. The electron radius re = 3.86 × 10−11 cm, the surface are Se ~ 10−20 cm2, the number of cells making up its surface Ne » 1045. P. Dirac looked for the value 1040 in the Universe. As a charged elementary cell is formed, clusters of deformed cells produced on its surface. On the surface of an electron a cluster is concave (negative curvature) and the surface of a positron is convex (positive curvature). Each cluster of electrons and positrons contains 4.17 × 1042 deformed cell. If these particles are closely contacted at the distance 3.86 × 10−11 cm, in the Coulomb interaction 4.17 × 1042 cells will take part while only one cell in the gravitational interaction! In this case we have a unique force relation
, and the size of an elementary cell is determined by the Compton length λ = ћ/mc. The electron radius re = 3.86 × 10−11 cm, the surface are Se ~ 10−20 cm2, the number of cells making up its surface Ne » 1045. P. Dirac looked for the value 1040 in the Universe. As a charged elementary cell is formed, clusters of deformed cells produced on its surface. On the surface of an electron a cluster is concave (negative curvature) and the surface of a positron is convex (positive curvature). Each cluster of electrons and positrons contains 4.17 × 1042 deformed cell. If these particles are closely contacted at the distance 3.86 × 10−11 cm, in the Coulomb interaction 4.17 × 1042 cells will take part while only one cell in the gravitational interaction! In this case we have a unique force relation
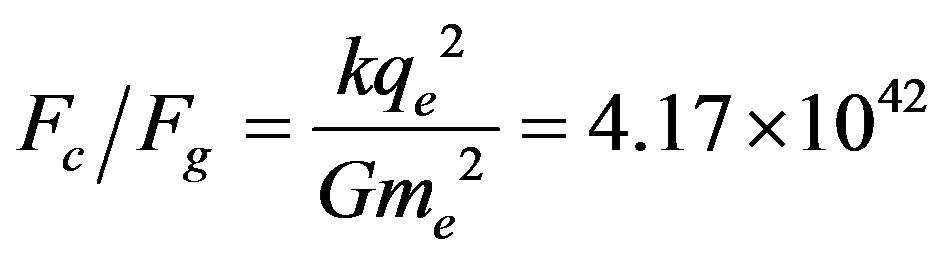
It is just this number that was looked for by the famous scientists: A. Eddington, H. Dicke, P. Dirac, L. Landau and many others.
Spiral cell deformation produces on the particle surface a pattern called a spin, it also up a magnetic field.
In 1913 N. Bohr introduced the concept of energy levels of hydrogen atom which occur at definite distances from the proton:
 .
.
At such distances space sets up ordered structures from deformed cells, clusters, already mentioned by us before. In case of a positronium a cluster on its surface contains 4.17 × 1042 cells whereas the electron surface has Ne ≈ 1045 cells. Consequently, an electron cannot be housed in such “Procrustean bed” and space forms the first energy level for an electron at the distance
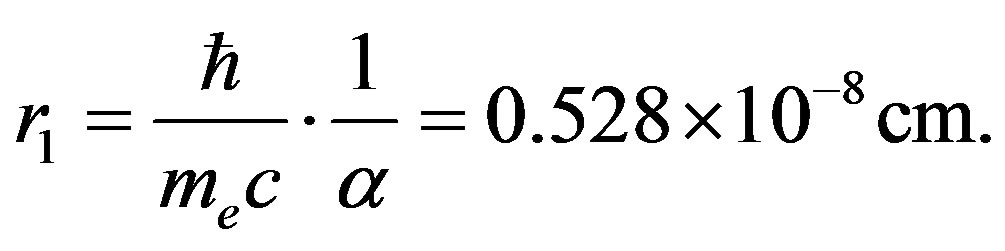
At such a distance the electron can stay in a hydrogen atom for an infinitely long time even though it offers a velocity (υe ~ c/137), a kinetic energy and a momentum.
It should be noted that the area of clusters on energy levels increases with the distance from a proton or a positron and, if the distance increases, for example, 4 times, the cluster area increases four-fold, too. The most surprising thing is that the electron is at rest in this case. It has already been mentioned above that the velocity υ in the granular space theory characterizes the deformation of elementary cells and acceleration a defines the gradient of this deformation. So both velocity and acceleration are more typical of rest rather than of motion. In more detail the granular space theory is presented in [4].
Since energy levels are set up by Colombian, magnetic and nuclear fields. It is not surprising that gravity fields can produce them, too.
In [3] we comprehensively studied the effect of energy level generation by the Earth. Photon clouds formed by electrons, as they pass from one level to another, produce quasi-blackbody radiation with T = 2.7 K and all the strange features of the Universe microwave background (CMB) are completely described by the peculiarities of the earth gravity and magnetic fields. To discover this effect will not demand billions of dollars. All that is needed for this is to provide one of the satellites launched for other purposes at a long distance with a primitive bolometer and to measure just the intensity (and not anisotropy) of CMB for one wavelength in the millimeter spectrum. And if this intensity coincides with the one measured on the Earth we may say that this radiation is “relict”. This cheapest astrophysical experiment (experimentum crucis) has not been performed for 45 years. Therefore, all theoretical arguments based on CMB “relictness” are premature before the experiment is realized. It is a pity that neither WMAP mission nor PLANK has measured this figure so far.
The idea that the Universe is made only of one element, a cell, enables us not to differentiate micro-, macroand megacosm. Consequently, energy levels can be set up by stars, galaxies and galaxy clusters.
There are very few stars with their masses are ten times bigger or smaller than the mass of the Sun but their radii very over wide limits. The size of the Sun, a common star whose amount is greatest in the Universe, R€~ 1011 cm, the surface area S€ ~ 1023 cm2, the gravitational radius rg = 3 × 105 cm, the area Sg ~ 1012 cm2. Let us consider a “gravitational atom” consisting of two stars of this size which resembles a positronium. If these two stars contracted to rg = 3 × 105 cm, the first gravitational level would be near one of them. The next levels would be at distances rn » rg × n2. If one of the stars is fixed, the second real star will be located on an energy level, with its cluster surface being equal to the surface of this star. The distance between these stars in this case:

In the vicinity of the Sun the mean distance between stars R is about 106 times larger than the mean diameter of the stars, then R ~ 1018 cm.
Analysis of nuclear IR radiation shows that a region with its cross-section of just 1 parsec, contains several millions of stars. It means that the distance between them R ~ 1016 cm.
A considerable number of stars (from 30 to 50%) from double, triple and other-fold systems. The effect of multiplicity is evidently a fundamental property of a huge number of stars. The components of such stars are very closely spaced, sometimes their surfaces are almost in contact. The average distance between the components of double stars is ~1013 cm.
Does this value contradict to the one we calculated above—∆Rs ~ 1016 cm. This difference can be simply explained: all the facts obtained recently in astronomy demonstrate that multiple systems were produced from a certain initial das-dust interstellar medium.
6. Dimensions of Galaxies and Their Clusters
Almost all galaxies are united in various groups and clusters numbering from 3 - 4 to several thousands of units. One of the largest clusters among them is Coma (or Veronica Hair). Its mass is Mc » 3 × 1015 M€. Masses of other rich clusters have the same order of magnitude. The gravitational radius of this cluster τg » 1021 cm and the surface Sg » 1042 cm2. Rg » 1023 cm is taken to be the size of an average galaxy in Coma cluster. The distance between the galaxies in this cluster
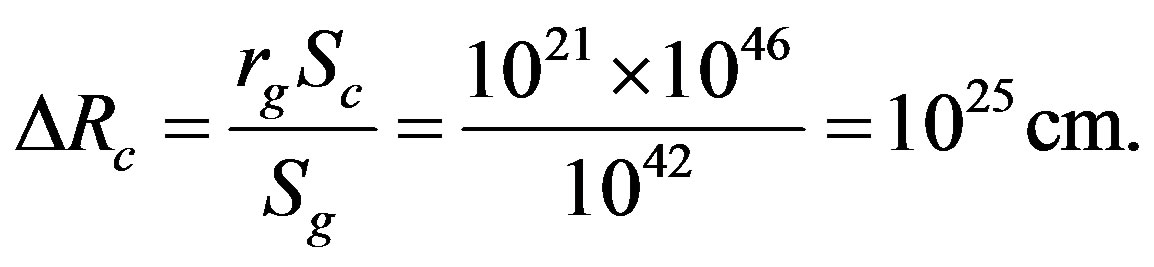
It may be suggested that this figure also determines the size of galaxies answering the question: what is responsible for it. Regular clusters are spherical in shape and have a strong concentration to the centre.
It is of great interest to apply the method, we used above, to find the distance between super clusters when we know that for Coma cluster Rk ~ 1025 cm, Sk ~ 1050 cm2
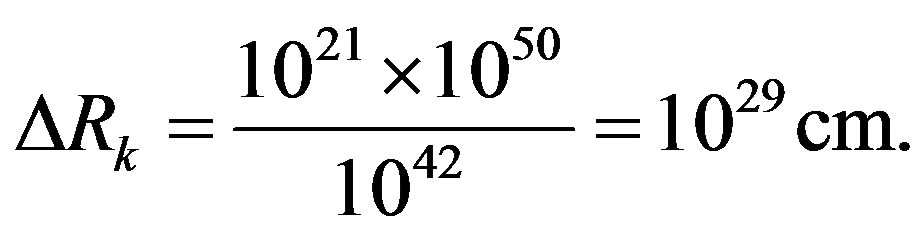
The size of the Universe, however, Ru ~ 1028 cm and hence super clusters cannot any longer produce something reminding of a spherical subsystem. Observations show that clusters and super clusters form something like a net structure. Extent super clusters are linked together and intersect; they serve as cell “walls”, and there are almost no galaxies inside them. We can give a few well-distinguished examples of such cells. The Universe has not larger systems than cells—cosmic hierarchy is broken on them.
7. The Only and Unique Universe
All the attempts to explain the red shift in galaxies spectra, the Doppler principle is not involved, have remained unsuccessful for over 100 years. The Doppler character of red shift is characterized by the quantity z
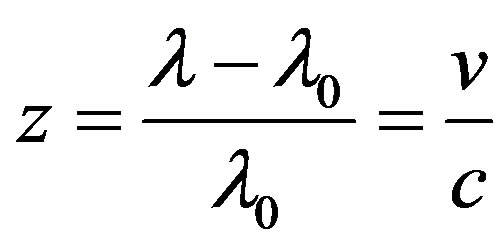
for low velocities υ/c < 1.
The Doppler nature of red shift plays the role of the “cornerstone” in the Universe “expansion” and even expansion with acceleration. In our work we have found another natural cause of the dependence z = υ/c by studying the behavior of the gravity potential φ set up by a huge number of galaxies in a certain volume with its radius R; by doing so we have corrected the mistake made by astronomers and cosmologists 100 years ago.
The old orthodox expansion theory predicted a tragic fate of the Universe which will have to disappear in many billions years for ever. The question arises: should the Universe have been born once in order to disappear then under cover of centuries?
The Universe cannot expand for another reason. In [2] we found the mass of one elementary cell mcell = 1.3 × 10−73 g,the mass of the Universe Mu ~ 10110 g and the original size of Universe development Ru ~ 10 km. This size is characteristic of a neutron star. So is this agreement accidental?
At the initial moment of Universe development there was neither space, no time and, consequently no “Big Bang”. We don’t know what matter formed the original “drop” and from where it appeared but at a certain moment the drop lost the equilibrium and began “to boil” intensively thus producing bubbles with their size L* ~ 10−33 cm. But the physical meaning of T and “boiling” differs from the modern one. Temperature is a macroscopic concept related to the kinetic energy of particles which form a system. Kinetic energy, in its term, depends on υ2. The granular space theory reveals the physical meaning of υ2/c2, the relative deformation of space cells. Thus, temperature is characteristic of cell deformation, too.
As far as the Universe “expansion” is concerned, it should be noted that when drifting apart galaxies move, nevertheless, in space consisting of cell and the Universe must constantly produce them, that is, contain an infinitely large amount of original matter. But, as opposed to mathematics, natural sciences do not admit either potential or actual infinity. Therefore the Universe itself escapes disappearance. For lack of Universe expansion, the cosmological constant introduced in Einstein’s theory of gravity Λ = 0.
In 1929 Einstein said: “Frankly speaking, we want not only to find out how nature is made, ··· but also, where possible, to attain an Utopian and bold aim, that is, to understand to understand why nature is like that.”
Now we can set forth some preliminary considerations not pretending to be rigorously proved but, nevertheless, having some important ideas.
One of the boldest wishes of theoretical physicists is to construct a theory which would provide us with uniquely observed values of all the parameters of elementary particles in the Universe.
The noble idealism of investigators makes us believe that a true theory describing the world must be unique and wonderful. In such a theory the parameters of elementary particles must be uniquely computable.
It should be noted that a sphere (a bubble) is the most economical three-dimensional figure. When the original “drop” “boils” the resultant bubbles on contact assume the form of a polyhedron. The next economical figure is 14-hedron whose shape is nearly spherical. Form this we might reason that, no matter what the original Universe was like, the space it can produce will consist of threedimensional elementary cells of the same shape.
Willer said [9]: “Only one quantity directly related to large numbers has clear and accessible interpretation in the existing theory, this is Planck length . So we should start our investigation with this quantity. Space is made of cells of such a size.” This idea opens quite new ways of studying the nature of electric charge, spin and the dimensions of elementary particles [2-7]. The geometry and the elastic properties of elementary cells play a large role in producing space bunches or elementary cells.
. So we should start our investigation with this quantity. Space is made of cells of such a size.” This idea opens quite new ways of studying the nature of electric charge, spin and the dimensions of elementary particles [2-7]. The geometry and the elastic properties of elementary cells play a large role in producing space bunches or elementary cells.
A fundamental assertion of this is the formation of clusters from deformed cells inside a particle and outside. The clusters inside the particle are calls quarks, and the deformed cells between quarks are gluons. Every cluster contains a colossal number of cells, therefore their quaint deformation allows introducing both color and fragrance and ascribing original properties to quarks and gluons. Spatial forms of bodies can measured in centimeters, feet and miles. In the same way mass is measured in grams, pounds and tons. In this case even the world constants , G, c will be characterized by different numbers but all dimensionless constants will retain the present-day values no matter what the Universe is like. Moreover the mass of neutron will always be larger than that of proton and electron together.
, G, c will be characterized by different numbers but all dimensionless constants will retain the present-day values no matter what the Universe is like. Moreover the mass of neutron will always be larger than that of proton and electron together.
Our Universe could have different properties such as mass, elasticity of matter, etc. but the geometry of three-dimensional cells lays down its conditions: both the mass and the dimensions of elementary cells would be proportional to the present-day values. In order to have absolute evidence for the uniqueness of the Universe, we must see a cell and a particle even in an imaginary experiment by increasing their dimensions to the size of a football. We should begin with an electron since it has the simplest structure. But an electron consists of 1068 cells and our effort to understand its structure are seemingly doomed to failure. But nature produces an electron in t ~ 10−21 second, whereas man has much more time for investigations.
Any physicist trying to construct an electron must take into account the following:
1) An electron has mass me and size re.
2) The radial deformation of cells creates on its surface a cluster of negative curvature and on the positron surface a cluster of positive curvature.
3) An electron must be formed at the same time with a positron—their clusters have the same size.
4) Spiral deformation of cells occurs simultaneously with radical deformation and forms a particle spin.
5) There is a very simple “latch” which does not allow space to destroy the electron surface. “Nature laughs at our problems,”—said A.Fresnel.
Along with traditional investigations on an accelerator, a search for electron size and mass must be begun already today. Even though we had now E ~ 1019 GeV at our disposal, we would learn nothing new about electron. But it is just the electron that serves as “a dam” which stops quite a flow of discoveries about the structure of the Universe.
Some of theoretical physicists will have to repeat Kepler’s deed who studied about 70 versions of Mars orbits before to found a true one. Although we shall have to reconsider hundreds of electron models, it is a little easier for us now than it was for Kepler as we have fastresponse computers at our disposal.
The Universe is a very complicated system so that it would be studied deductively starting from the initial conditions and by solving equations of motion. A much more fruitful approach is to analyze closely the observed properties of the Universe and then to try to draw conclusions regarding their nature and evolution in the past.
8. Conclusions
We have been mistaken for over one hundred years about the nature of the red shift in the spectrum of far-removed stars which gave birth to a hypothesis for Universe expansion (even with acceleration) and it would finally result in its full destruction.
The first cause of such a tragically hypothesis is an original behavior of the gravity field potential set up not by a single star or a galaxy but by the whole matter inside a shell with its radius R: φ ~ const × R2. This behavior of the potential simulates the Doppler’s effect which leads to a red shift in the spectrum
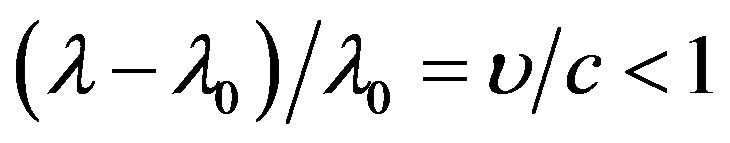 .
.
The second cause of absence of expansion is the fact that an increase in size of the Universe is demanded to make space of elementary cells which, in its turn, calls for matter, but the Universe cannot give infinitely much matter.
One of the circumstances responsible for the false treatment of the red shift was a change in the physical meaning of υ, a characteristic of gravitational potential. In the modern orthodox theory there is no velocity of incidence from a far distance on a sphere with its radius R and mass M but there exists the velocity of removal from this sphere. From the very beginning (1916) physicists should have known that, according to up-to-date measurements, these velocities are equal in modulus but are different in physical meaning.
It must be noted that the treatment of microwave background (CMB) as “relict” played into the hands of Universe expansion.
To check this hypothesis it is necessary, as it has been mentioned, that the first satellite launched at a large distance from the Earth must be equipped with a simple bolometer and intensity of CMB (but not anisotropy ΔT) is to be registered at least for one wavelength in the millimeter range. All this should have been done by astronomer as far back as 45 years ago.
Hubble was doubtful of the fact that the velocities in his formulas really describe the motion of galaxies in space. The purpose of his discovery was to demonstrate the proportion between galaxy distances and red shifts.
Gay-Lussac ДюПю made gas stream out of a vessel into vackum, that is, into another vessel preliminarily evacuated.
All the scientists observing the experiment were very much surprised to see that the temperature did not drop at all, the temperature of the whole gas remained constant!
A similar experiment was performed by Jonle J. P. and the temperature remained the same again, T1 = T2. So, the concept that the expanding Universe is cooling down is a point open to question.
Regarding galaxies again. The distance between them, R ~ 1025 cm, means that it is at this distance that space forms a gravity level where a gravitational cluster is generated, with its area being equal to that of the galaxy. This is the closest level. If the Universe were expanding, all the galaxies would be “sitting” in clusters whose dimensions would be many times larger than the galaxies. This conclusion once again shows that there is no expansion of the Universe again The question now arises: if the Universe does not expand, can it contract to a singular state? A typical and clear feature of modern physics is its tendency to reveal the inner unity of phenomena which seemed before not only to be related to each other but also unrelatable. The simplicity of a theory consists not in the mathematic form of its equations but in the results showing the inner unity of probably a wider range of phenomena.
When studying a hydrogen atom we observed a paradoxes effect: if we try to bring together an electron and a proton, r < 0.528 × 10−8 cm, we can see that unlike charges are not attracted together but repelled. The problem, in essence, is as follows: at shorter distances there are no clusters whose area would be equal to the electron surface. The liberated electron goes back at once to its original place—the ground energy level.
The unity of phenomena in nature enables us to state that a similar repulsion effect exists in the world of stars and galaxies as well. Take an “ideal” Universe where both stars and galaxies are born one by one without own (peculiar) velocities. In this case stars are born at rs ~ 1016 cm and galaxies at rc ~  cm, and space cannot bring them together. Such a Universe would be stable, and though stars and galaxies have, in actual fact, own velocities, the repulsion effect would exist for them too.
cm, and space cannot bring them together. Such a Universe would be stable, and though stars and galaxies have, in actual fact, own velocities, the repulsion effect would exist for them too.
Thermal death of the Universe is another factor responsible for life destruction. Stars will spend step by step light nuclear fuel—hydrogen and helium and then become extinct, won’t they? But in combustion stars liberate a huge amount of energy in various forms. Since the Universe is closed, all this energy has no outlet and it will destruct heavy atoms and stars on the whole.
And, finally, another proof of Universe stability. At present the gravitational potential on the boundary of the Universe, Ru ~ 1028 cm can be as high as φu ~ c2. If on the boundary of a massive star (“black hole”) φ = c2, no observer, including an attendant one, when moving outside can overcome the boundary of this star. In this case he would have to overcome the velocity of light. But it is impossible as the velocity of light, as noted above, characterizes the maximum deformation of elementary space cells. In other words, the granular space theory does not take into consideration any singularity: of stars and of the Universe on the whole. This comment makes us reconsider completely the effect of the so-called “gravitational collapse”. Inside a “black hole” there is nothing dangerous because we ourselves are living inside such a “hole” and the gravitational potential on the boundary of the Universe φ = c2. Consequently, all the physical processes on the boundary of the Universe stand still, the Universe cannot either expand or contract as the velocity of light c means maximum deformation of space cells. In [2] we gave some evidence for the impossibility of proton decay, so the Universe cannot be destructed and barions will always exist in it. All the material in this article shows that the experiment on measurements of intensity i rather than anisotropy  of cosmic microwave background (CMB) in the microwave frequency range far away from the Earth is of great importance for both cosmology and theory of elementary particles.
of cosmic microwave background (CMB) in the microwave frequency range far away from the Earth is of great importance for both cosmology and theory of elementary particles.
In studying new natural phenomena we must always remember the warning “Occama’s razor”: essences should not be multiplied beyond necessity.
Our aspiration for solving these mysteries of nature, no matter how complicated and intricate they are, lies in the nature of human spirit. The results, which wander off from our present-day knowledge, seem paradoxes and lead to new discoveries on the threshold of which we are standing now.
But we are sure that human intellect will resolve all mysteries even though we shall have to put a lot of efforts to it once Goethe said that to err is human, but restless spirit obeying the highest duty always strives for the truth.
9. Acknowledgements
I would like to thank V. Kubik for valuable discussions.
REFERENCES
- A. G. Riess, et al., “Supernova Search Team Collaboration,” Astronomic Journal, Vol. 116, No. 3, 1998, p. 1009. doi:10.1086/300499
- V. Konushko, “Weak Interaction and the Nature of Virtual Particles,” Journal of Modern Physics, Vol. 2, No. 2, 2011, pp. 45-57. doi:10.4236/jmp.2011.22009
- V. Konushko, “Gravitation Energy Level and the Nature of Microwave Background of Universe,” Journal of Modern Physics, Vol. 2, No. 4, 2011, pp. 175-187.
- V. Konushko, “Granular Space and the Problem of Large Numbers,” Journal of Modern Physics, Vol. 2, No. 5, 2011, pp. 289-300. doi:10.4236/jmp.2011.25038
- V. Konushko, “Lorentz’s Transformations and Gravitation in the Granular Space Theory,” Journal of Modern Physics, Vol. 2, No. 6, 2011, pp. 431-446. doi:10.4236/jmp.2011.26053
- V. Konushko, “Where Is the Time Arrow Flying?” Journal of Modern Physics, Vol. 2, No. 7, 2011, pp. 637-641. doi:10.4236/jmp.2011.27074
- V. Konushko, “Stability of Atoms, Causality in Elementary Processes and the Mistery of Interference and Hyroscope,” Journal of Modern Physics, Vol. 3, No. 3, 2012, pp. 224-232. doi:10.4236/jmp.2012.33032
- I. Karachentsev and A. Chernin, “Islands in the Dark- Energy Ocean,” Scientific American, Vol. 11, 2006, pp. 31-37.
- J. A. Wheller, “Einsteins Vision,” New York, 1968.

