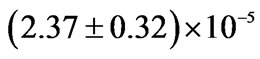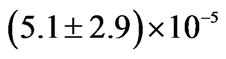Journal of Modern Physics
Vol.3 No.9(2012), Article ID:22716,6 pages DOI:10.4236/jmp.2012.39134
On the Extended Lorentz Transformation Model and Its Application to Superluminal Neutrinos
Department of Physics, Faculty of Sciences (I), Lebanese University, Beirut, Lebanon
Email: hamiehs@yahoo.fr
Received June 13, 2012; revised July 25, 2012; accepted August 4, 2012
Keywords: Natural Asset; Financial Value; Neural Network
ABSTRACT
In this paper, we consider the apparent superluminal speed of neutrinos in their travel from CERN to Gran Susso, as measured by the OPERA experiment, within the framework of the Extended Lorentz Transformation Model. The model is based on a natural extension of Lorentz transformation by wick rotation. Scalar and Dirac’s fields are considered and invariance under the new Lorentz group is discussed. Moreover, an extension of quantum mechanics to accommodate new particles is considered using the newly proposed Generalized-C quantum mechanics. A two dimensional representation of the new Dirac’s equation is therefore formulated and its solution is calculated.
1. Introduction
Recently, the OPERA collaboration, according to their precision measurement, claims [1] an early arrival time of CNGS (CERN Neutrino beam to Gran Sasso) muon antineutrinos traversing 730 kilometers from CERN to Gran Sasso. This corresponds to  . This larger deviation of the neutrino velocity from c is a new result pointing to new physics in the neutrino sector. The CNGS neutrinos have an average energy of 17 GeV with a broad distribution reaching up to several tens of GeV. A separate measurement of neutrinos above and below 20 GeV has revealed no significant energy-dependence of the superluminality in this energy range. The OPERA claim is compatible with earlier results obtained by the MINOS experiment at FERMILAB [2]. This result was recently confirmed in a new investigation by OPERA using a beam with a short-bunch. As we can see from Table 1. To understand the underlying physics, a large number of papers has been published in arXiv that can be categorized into models of geometric solutions in extra dimensions [3], deformed special relativity [4], environmental superluminality [5-7], and explicit Lorentz violation [8], and combinations of these ideas. While most of theories [9-12] are concerned about the Lorentz violation/modification, our main motivation here is the extension of Lorentz transformation using a natural mechanism namely a wick rotation via
. This larger deviation of the neutrino velocity from c is a new result pointing to new physics in the neutrino sector. The CNGS neutrinos have an average energy of 17 GeV with a broad distribution reaching up to several tens of GeV. A separate measurement of neutrinos above and below 20 GeV has revealed no significant energy-dependence of the superluminality in this energy range. The OPERA claim is compatible with earlier results obtained by the MINOS experiment at FERMILAB [2]. This result was recently confirmed in a new investigation by OPERA using a beam with a short-bunch. As we can see from Table 1. To understand the underlying physics, a large number of papers has been published in arXiv that can be categorized into models of geometric solutions in extra dimensions [3], deformed special relativity [4], environmental superluminality [5-7], and explicit Lorentz violation [8], and combinations of these ideas. While most of theories [9-12] are concerned about the Lorentz violation/modification, our main motivation here is the extension of Lorentz transformation using a natural mechanism namely a wick rotation via . As consequence of this transformation, a new dispersion relation is discovered which allows to probe a new velocity domain. The model will be applied to superluminal neutrino to obtain an estimation of neutrino mass. Moreover, as our main concern here is to probe new physics, we have considered the dynamics of superluminal particles not only within the framework of quantum mechanics but also in the generalized quantum mechanics [13].
. As consequence of this transformation, a new dispersion relation is discovered which allows to probe a new velocity domain. The model will be applied to superluminal neutrino to obtain an estimation of neutrino mass. Moreover, as our main concern here is to probe new physics, we have considered the dynamics of superluminal particles not only within the framework of quantum mechanics but also in the generalized quantum mechanics [13].
This paper is organized in the following manner. In the next section, the extended Lorentz transformation Model (ELTM), is presented and its application to neutrino is studied. In Section 3 application of ELTM to field theory is discussed. In Section 4 using the discovered dispersion relation a new Dirac’s equation (DE) within the framework of Generalized-C quantum mechanics (GCQM) is derived. Section 5 summarizes the results of the present investigation and also concluded remarks are given.
2. Modeling Superluminal Particles
The basic idea of the proposed Extended Lorentz Transformation Model (ELTM) is the observation that the Minkowski metric
Table 1. The summary of superluminal neutrinos from OPERA, MINOS.
| Experiment | Velocity ratios | Energy range |
| OPERA |
| 17 GeV |
| MINOS |
| 3 GeV |
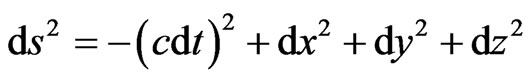
and the four-dimensional Euclidean metric

are equivalent if we make, Wick rotation, that is if one permits the coordinate ct to take on imaginary values1. Applying this rotation to Lorentz transformation, that is allowing c, which is the only parameter of special relativity, to take imaginary value  the space-time transformation becomes
the space-time transformation becomes  and
and
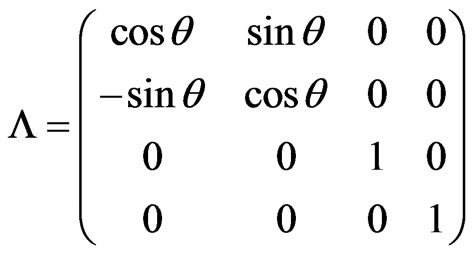
with 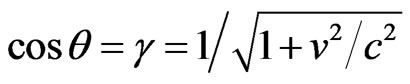 and, because of the Euclidian metric,
and, because of the Euclidian metric, . Clearly the symmetry group of such transformation is SO(4) with the properties that
. Clearly the symmetry group of such transformation is SO(4) with the properties that
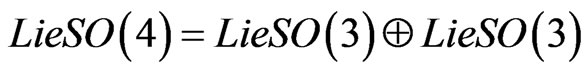
and its representation is equivalent to the tensor product of the two representations of SU(2) where the objects that transform under this representation are
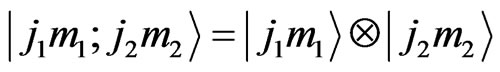
We observe that the new transformation extends the Lorentz transformation to a range of velocity2 v > c. Note that, in the ELTM, we avoid any necessity for imaginary masses in order to have v > c as done in tachyon theory. Thus sidestepping the problem of interpreting exactly what a complex-valued mass may physically mean. Other physical quantities can be obtained upon substitution of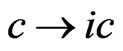 , in particular, a new dispersion relation can be found3
, in particular, a new dispersion relation can be found3
 (1)
(1)
3. Discussion about the Physical Interpretation of the Discovered Dispersion Relation
The found dispersion relation (Equation (1)) can have a physical interpretation as propagation of a wave in a medium with negative index of refraction (metamaterial). Moreover, the mass term 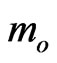 can be generated by a quantification in an extradimension without introducing the higgs field4. In fact, if we assume the following equation of motion
can be generated by a quantification in an extradimension without introducing the higgs field4. In fact, if we assume the following equation of motion
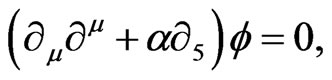
and by considering a wave solution to this equation with periodic boundary condition for Bosons5 in the quantified extradimension we can generate the mass term as
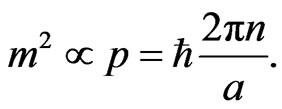
Here 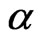 is complex and
is complex and 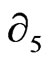 is the partial derivative with respect to the extradimension.
is the partial derivative with respect to the extradimension.
An important observation can be seen from this approach. By evaluating the angular momentum
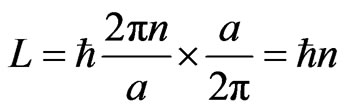 we found that
we found that

which is the Regge trajectory, one of the main motivation of string theory.
Moreover, the proposed dispersion relation Equation (1) introduce a limit to the maximum energy of the superluminal particles thus no need of renormalization group and perhaps a unified theory can emerge.
4. Application of the Model to the Opera Results
Applying Equation (1) to the Opera results, the neutrino mass can be extracted
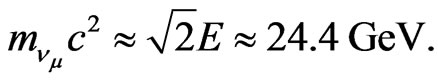
In Figure 1 we show E in GeV versus 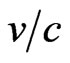 where we have fixed E = 17 GeV at
where we have fixed E = 17 GeV at 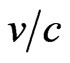 = 1 for neutrino. From the inner figure of Figure 1, we conclude that there is no significant energy-dependence of the superluminality at the vicinity of v ∼ c. Moreover, this result can be confronted to experimental results in the future if more superluminal particles (SP) are observed with large velocity ranges. These results, can be subject to two criticisms 1) The velocity dependence like shown in Figure 1 would lead to much larger deviations of neutrino velocity
= 1 for neutrino. From the inner figure of Figure 1, we conclude that there is no significant energy-dependence of the superluminality at the vicinity of v ∼ c. Moreover, this result can be confronted to experimental results in the future if more superluminal particles (SP) are observed with large velocity ranges. These results, can be subject to two criticisms 1) The velocity dependence like shown in Figure 1 would lead to much larger deviations of neutrino velocity
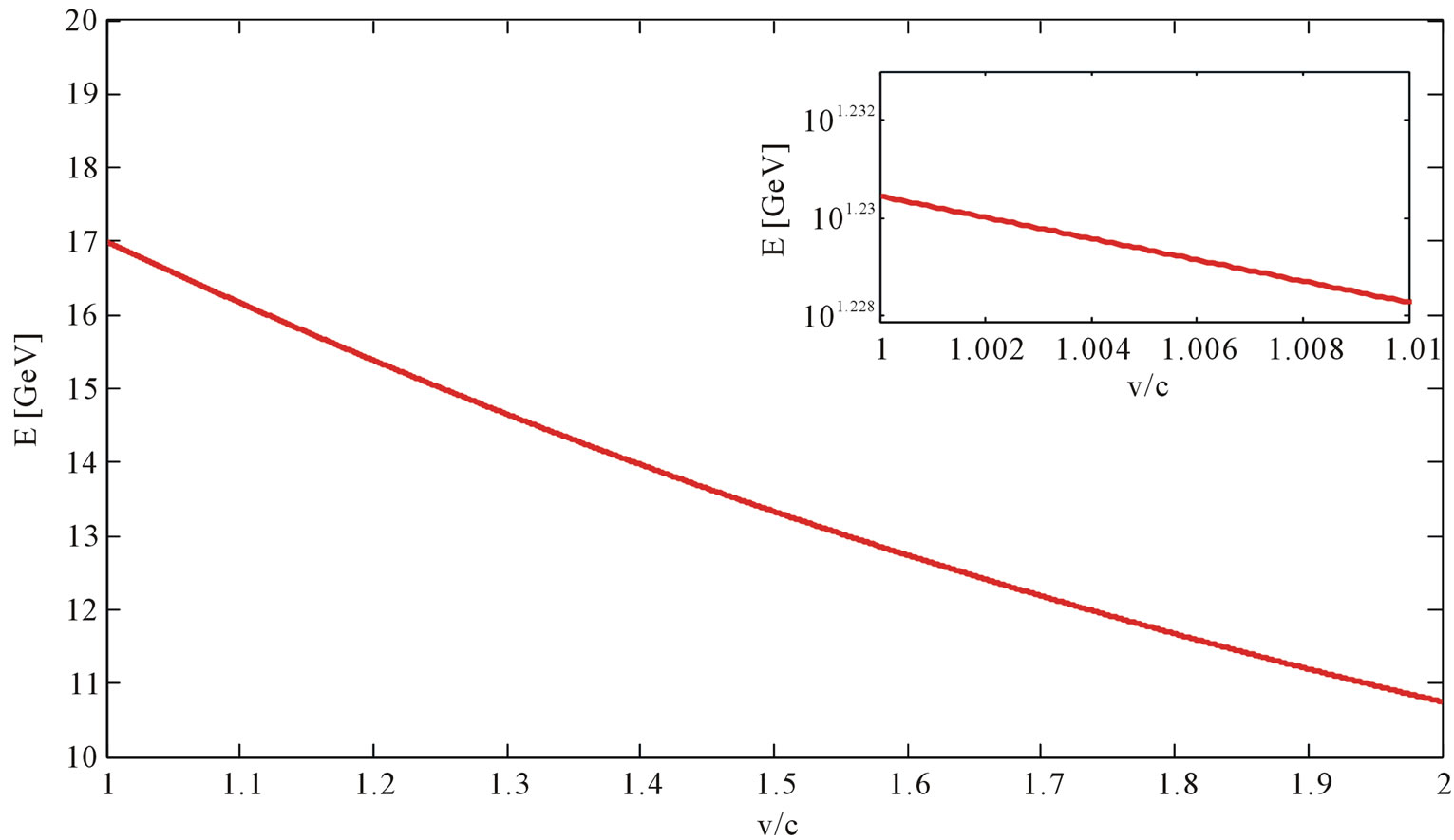
Figure 1. E in GeV as function of 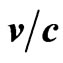 for superluminal neutrino.
for superluminal neutrino.
from c than suggested by Opera: a large range of neutrino energies from few GeV to 80 GeV needs to be considered.
2) Also, Equation (1) does not allow real energies for neutrino momenta above m0c2 = 24.4 GeV. This contradicts the observations from Z decay at LEP where neutrinos with energy 45.6 GeV were produced.
However, since enough experimental data for massmatrix of the neutrinos under consideration is still absent, it is not clear its exact form for the superluminal neutrino. Here, we claim the following:
“If nature allows the existence of superluminal particles they must obey to the proposed dynamics.”
In Figure 2 we show the neutrino E as function of pc for particle/antiparticle and SP/anti-SP (4 branches). From Figure 2 we expect that the neutrino becomes superluminal at the 4 points of intersection of the circle describing the Superluminal neutrino and the lines describing neutrino. We call this mechanism as the superluminality mechanism for zero mass particles.
5. Application of the ELTM to Field Theory
In order to show that our approach is not a simple transformation from Minkowski space to Euclidian space, which transforms the action 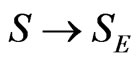 6, we consider the application of the model to complex local field theory. Consider as an example, a scalar field with the dispersion relation given above (Equation (1)) and defining
6, we consider the application of the model to complex local field theory. Consider as an example, a scalar field with the dispersion relation given above (Equation (1)) and defining
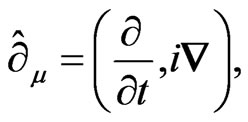
then, the field equation can be written as 
 (2)
(2)
with 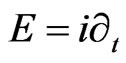 and
and . The field equation written at this form, that is using the
. The field equation written at this form, that is using the  form, is used to conserve properties like covariant and contravariant. This will simplify the discussion of invariance under the following extended Lorentz transformation7
form, is used to conserve properties like covariant and contravariant. This will simplify the discussion of invariance under the following extended Lorentz transformation7

where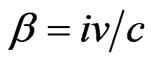 , and
, and . The invariance of Equation (2) can now be deduced from the invariance of the scalar field in standard field. After studying invariance of the new scalar field, it is useful to see what happen for the dynamical quantities like Green’s function. We start our discussion from the wick-rotated8 functional integral of
. The invariance of Equation (2) can now be deduced from the invariance of the scalar field in standard field. After studying invariance of the new scalar field, it is useful to see what happen for the dynamical quantities like Green’s function. We start our discussion from the wick-rotated8 functional integral of 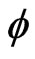

With 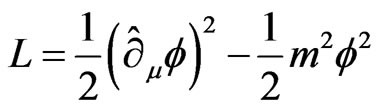 is the Lagrangian density for the free scalar field. The generating function of
is the Lagrangian density for the free scalar field. The generating function of  is
is
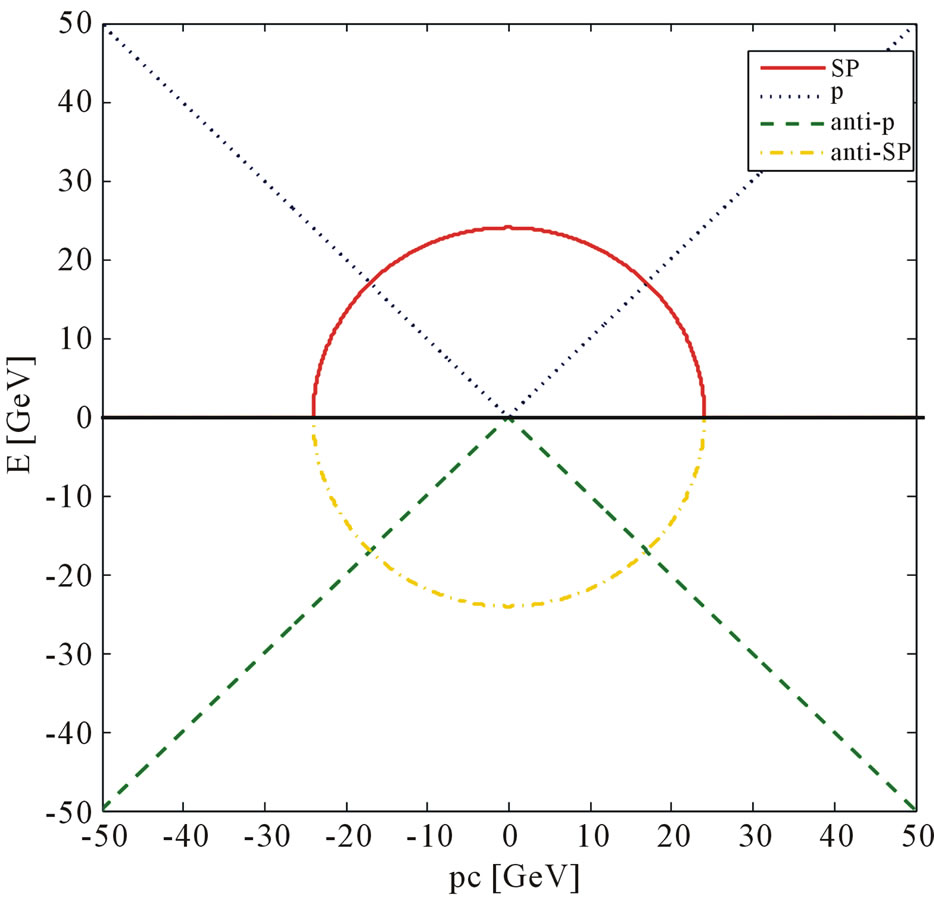
Figure 2. E in GeV as function of pc in GeV: Solid line for SP; Dotted line for particle; Dashed line for antiparticle; Dashed dotted line anti-SP.
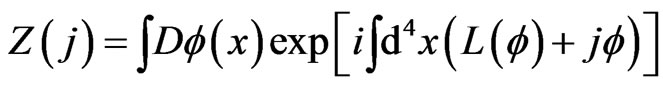
Therefore, the Green’s function integral of 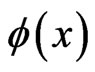 can be calculated from the generating function exactly as Minkowski Green’s function that is
can be calculated from the generating function exactly as Minkowski Green’s function that is

This Green’s function, is just the Feynman propagator with
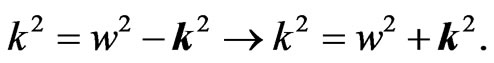
As for the Dirac field, it is also possible to construct its wave equation. In fact, the proposed DE for SP that must be invariant under the extended Lorentz transformation is
 .
.
Of course, this equation can be guessed from the non superluminal particles (NSP) DE. Again, as done for scalar field, the Lorentz invariance of this equation, under the extended Lorentz group, can be deduced from the invariance of the NSP. In fact, the generators of the Lee algebra of the extended Lorentz group will be the same as Lorentz group algebra. The only change is in the antisymmetric tensor that gives the infinitesimal angle where 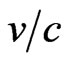 must be replaced by
must be replaced by 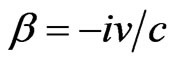 (see any standard field theory text book). Moreover, solution of this equation can be obtained from the NSP solution of DE using the following substitution
(see any standard field theory text book). Moreover, solution of this equation can be obtained from the NSP solution of DE using the following substitution
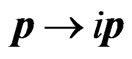 (3)
(3)
in Dirac’s spinors. Thus the positive energy solution fourspinors is

and the negative energy solution is
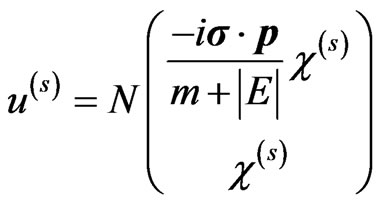
where N is a normalization factor and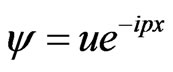 . Other physical quantities for Dirac field can be obtained by the same substitution given in Equation (3). For example when calculating cross-section for some physical process in standard model one has to take into account for SP the
. Other physical quantities for Dirac field can be obtained by the same substitution given in Equation (3). For example when calculating cross-section for some physical process in standard model one has to take into account for SP the 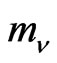 and the substitution of
and the substitution of
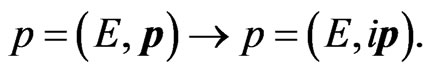
For example, the scattering cross section of superluminal  can be inferred from the subluminal scattering for the same process. In fact we found
can be inferred from the subluminal scattering for the same process. In fact we found
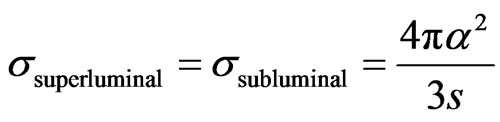
Application of this formalism to interacting fields and calculation of cross section for some physical process will be left for future investigation. In next section, as we are interested in new physics that might govern the dynamics of SP, we take this opportunity to see the smallest representation of the new DE in the newly proposed algebra [13]. This algebra is called the Generalized-C (GC) extend quantum theory to new class of theories based on the non associative algebra.
6. Beyond Local Complex Field Theory Description of SP
Since our aim in this paper is to search for new physics that describe SP then it is of great importance to investigate the new DE within the framework of the extended quantum mechanics that has been recently proposed in [13]. In fact, Quantum mechanics as developed in the standard textbooks, and as applied to elementary particle physics in the standard model, is understood to be complex quantum mechanics: the wave functions and probability amplitudes are represented by complex numbers. However, it has been known since the 1930s that more general quantum mechanical systems can, in principle, be constructed.
In the present work, the Generalized-C quantum mechanics [13] is studied for SP. However, we do not construct, a general formalism for Generalized-C local field theory. We only concentrate on the description of the new DE within the framework of Generalized-C quantum mechanics. We believe that this will be useful in future investigation of new physics. For clarity, to avoid the explicit use of i, the most general form of DE is9
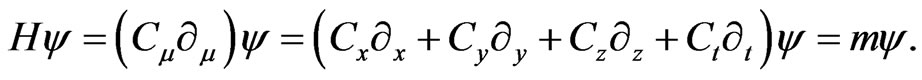 (4)
(4)
To recover the new Klein-Gordon equation
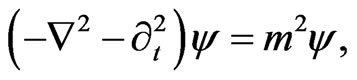
the following conditions must hold
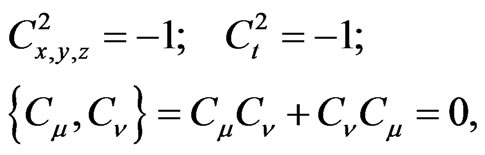 (5)
(5)
where

Using the following Dirac matrices, satisfying (5)
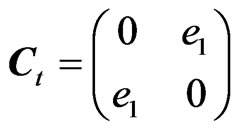

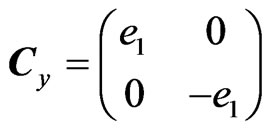
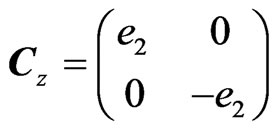
(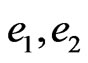 are the imaginary GC units, see Appendix), in Equation (4) results in:
are the imaginary GC units, see Appendix), in Equation (4) results in:
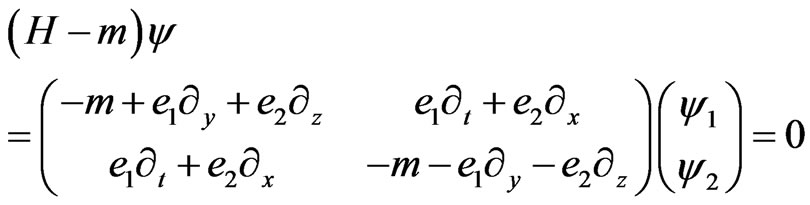
The solution to this equation in 1 + 1 dimension, y, t, is

where, as usual p represents the “momentum”, E is the “energy” and N is a normalization factor. As expected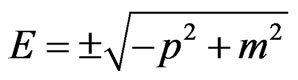 . Note that the importance of GC algebra is in the existence of complex solution in small dimension (here 2) which is not available in C algebra.
. Note that the importance of GC algebra is in the existence of complex solution in small dimension (here 2) which is not available in C algebra.
7. Conclusion
We have attempted to account for neutrino superluminality, as reported by OPERA, while staying within the familiar framework of local field theory. We show that superluminal neutrinos can be fitted into the original Standard Model without changing other results. Since enough experimental data for mass-matrix of the neutrinos is still absent, it is not clear what is the exact form of it. However, using the extended Lorentz transformation model we have provided an estimation of this mass. It is also found, in this paper, a two dimensional Dirac’s wave function for the new dispersion relation within the framework of the three dimensional non-associative algebra. Finally we believe that the proposed models merits to be explored in more physical problem.
8. Acknowledgements
The author is very grateful to D. T. Elkhechen for very useful discussions. This work was performed as part of the research program of Doctorate School of Science and Technology.
REFERENCES
- T. Adam, et al., “Measurement of the Neutrino Velocity with the OPERA Detector in the CNGS Beam,” arXiv: 1109.4897, 2011.
- P. Adamson, et al., “Measurement of Neutrino Velocity with the MINOS Detectors and NuMI Neutrino Beam,” Physical Review D, Vol. 76, No. 7, 2007, Article ID: 072005. doi:10.1103/PhysRevD.76.072005
- S. S. Gubser, “Superluminal Neutrinos and Extra Dimensions,” Physics Letters B, Vol. 705, No. 3, 2011, p. 279. doi:10.1016/j.physletb.2011.10.028
- G. Amelino-Camelia, L. Freidel, J. Kowalski-Glikman and L. Smolin, “OPERA Neutrinos and Deformed Special Relativity,” arXiv:1110.0521, 2011.
- G. Dvali and A. Vikman, “Price for Environmental Neutrino-Superluminality,” arXiv:1109.5685, 2011.
- A. Kehagias, “Relativistic Superluminal Neutrinos,” arXiv: 1109.6312, 2011.
- I. Oda and H. Taira, “Superluminal Neutrinos from Gauge Field,” arXiv:1110.0931, 2011.
- J. Alexandre, J. Ellis and N. E. Mavromatos, “On the Possibility of Superluminal Neutrino Propagation,” arXiv: 1109.6296, 2011.
- B. Alles, “Relativity Accommodates Superluminal Mean Velocities,” arXiv:1111.0805, 2011.
- L. Iorio, “Environmental Fifth-Force Hypothesis for the OPERA Superluminal Neutrino Phenomenology: Constraints from Orbital Motions around the Earth,” arXiv: 1109.6249, 2011.
- E. Saridakis, “Superluminal Neutrinos in Horava-Lifshitz gravity,” arXiv:1110.0697, 2011.
- J. S. Diaz and V. A. Kostelecky, “Three-Parameter Lorentz-Violating Texture for Neutrino Mixing,” Physics Letters B, Vol. 700, No. 5, 2011, p. 25. doi:10.1016/j.physletb.2011.04.049
- S. Hamieh and H. Abbas, “Two Dimensional Representation of the Dirac Equation in Non Associative Algebra,” arXiv:1104.3416, 2011.
- S. Adler, “Quaternion Quantum Mechanics and Quantum Fields,” Oxford University Press, New York, 1995.
Appendix
We remind the reader about the properties of the Generalized-C algebra (GC). An interested reader may refer to [13,14] for further information. The proposed generalization of the C algebra, the GC, is finite-dimensional non division algebra10 containing the real numbers R as a sub-algebra and has the following properties:
• A general GC number, q, can be written as

where
The real  and the imaginary GC units,
and the imaginary GC units,  are defined by
are defined by
• 
• The addition is defined as
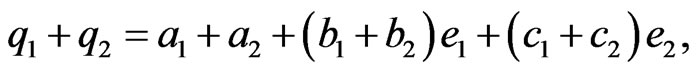
is associative
• 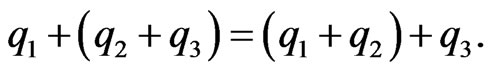
• The multiplication is defined as
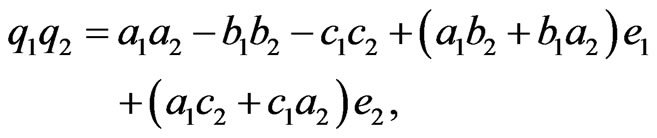
is non-associative under multiplication that is  .
.
• The norm of an element q of GC is defined by

with the GC conjugate  given by
given by
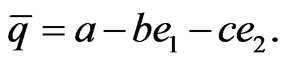
NOTES
1The Minkowski metric becomes Euclidean when ct is restricted to the imaginary axis, and vice versa. Taking a problem expressed in Minkowski space with coordinates x, y, z, t, and substituting ct = icτ, sometimes yields a problem in real Euclidean coordinates x, y, z, τ, which is easier to solve. This solution may then, under reverse substitution, yield a solution to the original problem.
2The foundations of special relativity are the relativity principle and the invariance of the speed of light. As a result, the Galilei group of classical mechanics is replaced by the Lorentz group, which leads, for example, to the relativistic law of addition of velocities. The fact that the speed of light is the maximum attainable velocity of all particles does not directly follow from the Lorentz group, since it only delivers an invariant velocity at first.
3Note that  correspond to
correspond to  and
and  correspond to v = c.
correspond to v = c.
4Work in progress.
5Note that for fermion we must assume antiperiodic boundary conditions.
6A transformation from quantum to statistical mechanics.
7Note that, this representation of  which transform
which transform 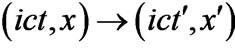 is used to conserve the Minkwovsi metric. One can use another variant of the new Lorentz transformation matrix that transform
is used to conserve the Minkwovsi metric. One can use another variant of the new Lorentz transformation matrix that transform 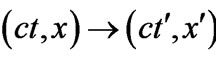 . However, in this case, the invariance is not straightforward because the use of Euclidean
. However, in this case, the invariance is not straightforward because the use of Euclidean  metric is essential.
metric is essential.
8By wick-rotated we mean the transformation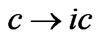 .
.
9From now on, the positions of the indices, μ, ν etc have no significance with respect to covariance or contravariance and are placed for typographical convenience. Repeated indices, however, do indicate summation.
10A division algebra, is a finite dimensional algebra for which a ≠ 0 and b ≠ 0 implies ab ≠ 0, in other words, which has no nonzero divisors of zero.