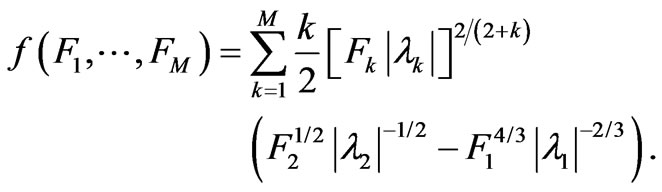Journal of Modern Physics
Vol.2 No.11(2011), Article ID:8646,7 pages DOI:10.4236/jmp.2011.211171
Direct Fisher Inference of the Quartic Oscillator’s Eigenvalues
1Universidad Nacional de La Plata, Facultad de Ingeniera, Área Departamental de Ciencias Básicas, La Plata, Argentina
2Universidad Nacional de La Plata, Instituto de Fsica (IFLP-CCT-CONICET), La Plata, Argentina
3Universitat de les Illes Balears and IFISC-CSIC, Palma de Mallorca, Spain
4CREG-Universidad Nacional de La Plata-CONICET, La Plata, Argentina
5Instituto Carlos I de Fisica Teorica y Computacional and Departamento de Fisica Atomica, Molecular y Nuclear, Universidad de Granada, Granada, Spain
E-mail: angeloplastino@gmail.com
Received June 22, 2011; revised July 30, 2011; accepted August 23, 2011
Keywords: Information Theory, Fisher’s Information Measure, Legendre Transform, Quartic Anharmonic Oscillator
ABSTRACT
It is well known that a suggestive connection links Schrödinger’s equation (SE) and the information-optimizing principle based on Fisher’s information measure (FIM). It has been shown that this entails the existence of a Legendre transform structure underlying the SE. Such a structure leads to a first order partial differential equation (PDE) for the SE’s eigenvalues from which a complete solution for them can be obtained. We test this theory with regards to anharmonic oscillators (AHO). AHO pose a long-standing problem and received intense attention motivated by problems in quantum field theory and molecular physics. By appeal to the Cramer Rao bound we are able to Fisher-infer the energy eigenvalues without explicitly solving Schrödinger’s equation. Remarkably enough, and in contrast with standard variational approaches, our present procedure does not involve free fitting parameters.
1. Introduction
It is well-known that a strong link exists between Fisher’ information measure (FIM) I [1] and Schrödinger wave equation (SE) [2-7]. In a nutshell, this connection is based upon the fact that a constrained Fisher-minimizetion leads to a SE-like equation [1-7]. In turn, this implies the existence of intriguing relationships between various SE-facets, and Jaynes’s maximum entropy principle. In particular, basic SE-consequences such as the Hellmann-Feynman and the Virial theorems can be reinterpreted in terms of a special kind of reciprocity relations between relevant physical quantities, similar to the ones exhibited by the thermodynamics’ formalism via its Legendre-invariance property [5,6]. This fact demonstrates that a Legendre-transform structure underlies the non-relativistic Schrödinger equation. As a consequence, the possible energy-eigenvalues are now seen to be constrained by such structure in a rather unsuspected way [5-7], a fact that allows one to obtain a first-order differential equation, unrelated to Schroedinger’s equation [7], that energy eigenvalues must necessarily satisfy. The predictive power of this new equation will be explored here.
We will apply our formalism here to the quantum anharmonic oscillator, which is the paradigmatic testingground for new approaches to Schroedinger eigenvalue equation. Besides their intrinsic conceptual and mathematical interest, anharmonic oscillators have received considerable attention over the years due to their practical relevance in connection with several areas of physics, such as quantum field theory and molecular physics, among others. In this kind of systems, the most intense focus has been traditionally concentrated upon the quartic oscillator. General accounts containing illuminating references on this problem may be found, for instance, in [8]. Note that a perturbation series solution to this problem in powers of the anharmonicity-parameter ![]() is divergent-asymptotic for all
is divergent-asymptotic for all  [9]. Specifically, we will apply our procedure to treat the quartic anharmonic oscillator. By appeal to the Cramer Rao bound we obtain the particular solution that leads to the system’s eigenvalues without need of explicitly solving Schrödinger’s equation. More importantly, we do not need to appeal to any arbitrary or empirical parameter, as is common practice in other treatments [10]. The parameter-free nature of our treatment is evidence of the structural physical information that we incorporate to the theory via Fisher's information measure.
[9]. Specifically, we will apply our procedure to treat the quartic anharmonic oscillator. By appeal to the Cramer Rao bound we obtain the particular solution that leads to the system’s eigenvalues without need of explicitly solving Schrödinger’s equation. More importantly, we do not need to appeal to any arbitrary or empirical parameter, as is common practice in other treatments [10]. The parameter-free nature of our treatment is evidence of the structural physical information that we incorporate to the theory via Fisher's information measure.
2. Basic Ideas
Let x be a stochastic variable and 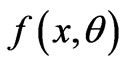 the probability density function (PDF) for this variable, which depends on the parameter
the probability density function (PDF) for this variable, which depends on the parameter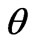 . If an observer were to make a measurement of x and had to best infer
. If an observer were to make a measurement of x and had to best infer 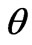 from such measurement, calling the resulting estimate
from such measurement, calling the resulting estimate , one might ask how well could
, one might ask how well could  be determined. Estimation theory [1] tells us that the best possible estimator
be determined. Estimation theory [1] tells us that the best possible estimator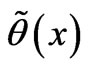 , after a very large number of x-samples is examined, suffers a mean-square error
, after a very large number of x-samples is examined, suffers a mean-square error  from
from  obeying the rule
obeying the rule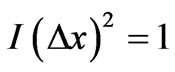 , where I is an information quantifier called the Fisher information measure (FIM), a non linear functional of the PDF that reads
, where I is an information quantifier called the Fisher information measure (FIM), a non linear functional of the PDF that reads
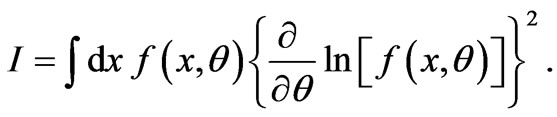 (1)
(1)
Any other estimator must have a larger mean-square error (all estimators must be unbiased, i.e., satisfy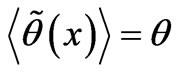 ). Thus, FIM has a lower bound. No matter what the parameter
). Thus, FIM has a lower bound. No matter what the parameter 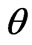 might be, I has to obey
might be, I has to obey
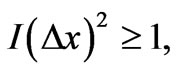 (2)
(2)
the celebrated Cramer-Rao bound [1].
In the case of physical Fisher applications, the particular instance of translational families has received a great deal of attention in the literature [1]. These are mono-parametric distribution families of the form 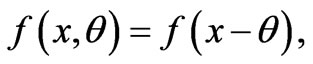 known up to the shift parameter
known up to the shift parameter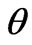 . All family members exhibit identical shape. For such families one gets
. All family members exhibit identical shape. For such families one gets
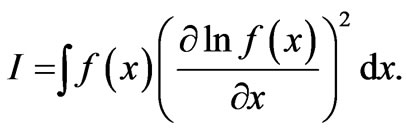 (3)
(3)
Focus attention now a system that is specified by a set of M physical parameters . We can write
. We can write  with
with 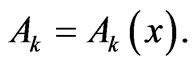 The set of
The set of 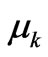 -values is to be regarded as our prior knowledge. It represents our available empirical information. Let the pertinent probability distribution function (PDF) be
-values is to be regarded as our prior knowledge. It represents our available empirical information. Let the pertinent probability distribution function (PDF) be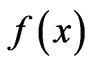 . Then,
. Then,
 (4)
(4)
In this context it can be shown (see for example [2,3]) that the physically relevant PDF 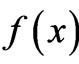 minimizes FIM subject to the prior conditions and the normalization condition. Normalization entails
minimizes FIM subject to the prior conditions and the normalization condition. Normalization entails  and, consequently, our Fisher-based extremization problem adopts the appearance
and, consequently, our Fisher-based extremization problem adopts the appearance
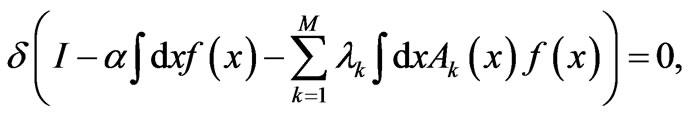 (5)
(5)
where we have introduced the 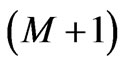 Lagrange multipliers
Lagrange multipliers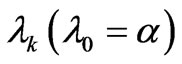 . In Ref. [2] one can find the details of how to go from (5) to a Schrödinger’s equation (SE) that yields the desired PDF in terms of the amplitude
. In Ref. [2] one can find the details of how to go from (5) to a Schrödinger’s equation (SE) that yields the desired PDF in terms of the amplitude 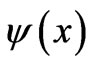 defined by
defined by . This SE is of the form
. This SE is of the form
 (6)
(6)
and can be formally interpreted as the (real) Schrödinger equation (SE) for a particle of unit mass ( ) moving in the effective, “information-related pseudo-potential”
) moving in the effective, “information-related pseudo-potential” 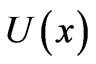 [2] in which the normalization-Lagrange multiplier (
[2] in which the normalization-Lagrange multiplier (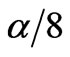 ) plays the role of an energy eigenvalue. The
) plays the role of an energy eigenvalue. The 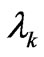 are fixed, of course, by recourse to the available prior information. In the case of one-dimensional scenarios,
are fixed, of course, by recourse to the available prior information. In the case of one-dimensional scenarios, 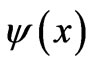 is real [11] and
is real [11] and
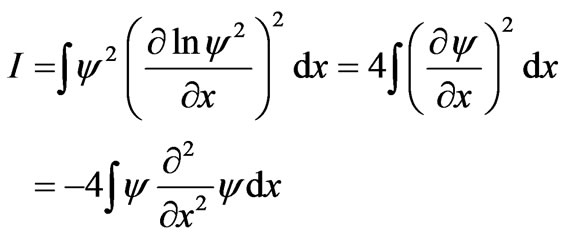 (7)
(7)
so that using the SE (6) we obtain
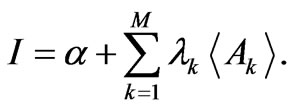 (8)
(8)
Legendre Structure
The connection between the variational solutions f and thermodynamics was established in Refs. [2] and [4] in the guise of reciprocity relations that express the Legendre-transform structure of thermodynamics. They constitute its essential formal ingredient [12] and were rederived à la Fisher in [2] by recasting (8) in a fashion that emphasizes the role of the relevant independent variables,
 (9)
(9)
Obviously, the Legendre transform main goal is that of changing the identity of our relevant variables. As for I we have
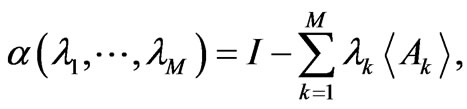 (10)
(10)
so that we encounter the three reciprocity relations (proved in [2])
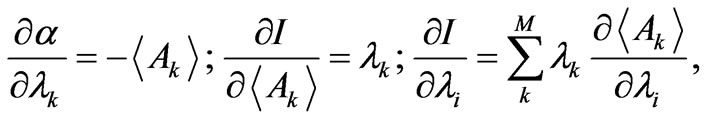 (11)
(11)
the last one being a generalized Fisher-Euler theorem.
3. Fisher Measure and Quantum Mechanical Connection
Since 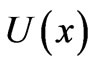 belongs to
belongs to  and thus admits of a series expansion in the powers-of-x-basis x,
and thus admits of a series expansion in the powers-of-x-basis x, 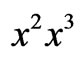 ,
,  [13]. Of course, the
[13]. Of course, the  themselves also belong to
themselves also belong to . They can thus be series-expanded in similar fashion, which enables one to base future considerations on the hypothesis that the prior-knowledge refers to powers
. They can thus be series-expanded in similar fashion, which enables one to base future considerations on the hypothesis that the prior-knowledge refers to powers , i.e.,
, i.e., . Assume then that one has gathered information concerning M moments
. Assume then that one has gathered information concerning M moments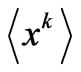 . The “information” potential U acquires the aspect
. The “information” potential U acquires the aspect
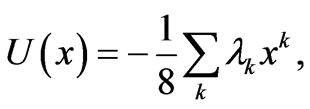 (12)
(12)
and we consider that the first M summands suffice to obtain a satisfactory representation of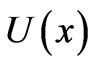 . Of course, our Lagrange multipliers are now to be identified with
. Of course, our Lagrange multipliers are now to be identified with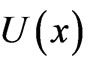 ’s series-expansion’s coefficients.
’s series-expansion’s coefficients.
For such Schrödinger-platform the virial theorem reads [5]
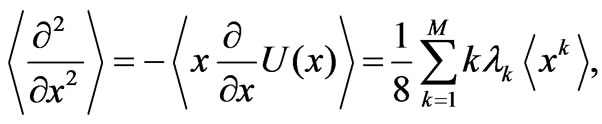 (13)
(13)
and thus, from (7) and (13) a virial-related expression for Fisher’s information measure can be obtained [5] in the fashion
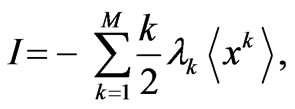 (14)
(14)
Now, substituting such I-form into (8) and solving for ![]() we find
we find
 (15)
(15)
 is explicit function of the M Lagrange multipliers —
is explicit function of the M Lagrange multipliers — ’s series-expansion coefficients
’s series-expansion coefficients 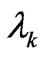 (the physical parameters
(the physical parameters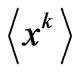 ). Equations (14) and (15) encode in adequate fashion the information provided by the virial theorem [5,6].
). Equations (14) and (15) encode in adequate fashion the information provided by the virial theorem [5,6].
3.1. Fisher-Schröedinger Legendre Structure
Interestingly enough, the reciprocity relations (RR) (11) can be re-derived on a strictly pure quantum mechanical basis [5], starting from 1) the quantum Virial theorem [which leads to Equations (14) and (15)] plus 2) information provided by the quantum HellmannFeynman theorem.
This fact indicates that a Legendre structure underlays the one-dimensional Schröedinger equation [5]. Thus, with , our “new” reciprocity relations are given by
, our “new” reciprocity relations are given by
 (16)
(16)
FIM expresses a relation between the independent variables or control variables (the prior information) and I. Such information is encoded into the functional form
 . For later convenience, we will also denote such a relation or encoding as
. For later convenience, we will also denote such a relation or encoding as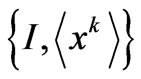 . We see that the Legendre transform FIM-structure involves eigenvalues of the “information-Hamiltonian” and Lagrange multipliers. Information is encoded in I via these Lagrange multipliers, i.e.,
. We see that the Legendre transform FIM-structure involves eigenvalues of the “information-Hamiltonian” and Lagrange multipliers. Information is encoded in I via these Lagrange multipliers, i.e., 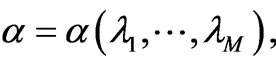 together with a bigection
together with a bigection 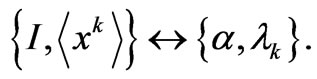
3.2. Two Scenarios
In a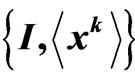 —scenario, the
—scenario, the  are functions dependent on the
are functions dependent on the  -values. As shown in [6], substituting the RR given by (16) in (14) one is led to a linear, partial differential equations (PDE) for I,
-values. As shown in [6], substituting the RR given by (16) in (14) one is led to a linear, partial differential equations (PDE) for I,
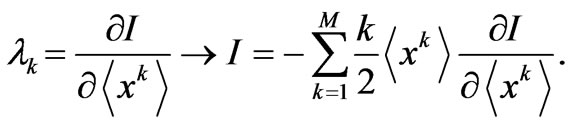 (17)
(17)
and a complete solution is given by
 (18)
(18)
where 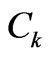 are positive real numbers (integration constants). The I-domain is
are positive real numbers (integration constants). The I-domain is
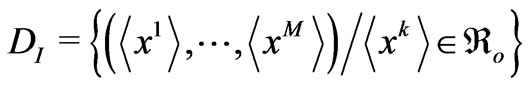 . Equation (18) states that for
. Equation (18) states that for , I is a monotonically decreasing function of
, I is a monotonically decreasing function of , and as one expects from a “good” information measure [1], I is a convex function. We may obtain
, and as one expects from a “good” information measure [1], I is a convex function. We may obtain  from the reciprocity relations (16). For
from the reciprocity relations (16). For 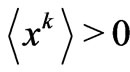 one gets,
one gets,
 (19)
(19)
and then, using (8), we obtain the![]() —normalization Lagrange multiplier.
—normalization Lagrange multiplier.
The general solution for the I—PDE does exist and its uniqueness has been demonstrated via an analysis of the associated Cauchy problem [6]. Thus, Equation (18) implies what seems to be a kind of “universal” prescription, a linear PDE that any variationally (with constraints) obtained FIM must necessarily comply with.
In the 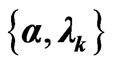 scenario, the
scenario, the  are functions that depend on the
are functions that depend on the  -values. As we showed in [7], an analog
-values. As we showed in [7], an analog ![]() -PDE exists. Substituting the RR given by (16) in (15) we are led to
-PDE exists. Substituting the RR given by (16) in (15) we are led to
 (20)
(20)
and a complete solution is given by
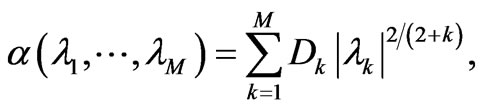 (21)
(21)
where the  s are positive real numbers (integration constants). The
s are positive real numbers (integration constants). The ![]() -domain is
-domain is 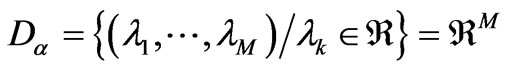 . Also, Equation (21) states that for
. Also, Equation (21) states that for ,
, ![]() is a monotonically decreasing function of the
is a monotonically decreasing function of the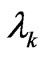 , and as one expect from the Legendre transform of I, we end up with a concave function. We may obtain the
, and as one expect from the Legendre transform of I, we end up with a concave function. We may obtain the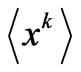 ’s from the reciprocity relations (16). For
’s from the reciprocity relations (16). For 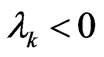 one gets
one gets
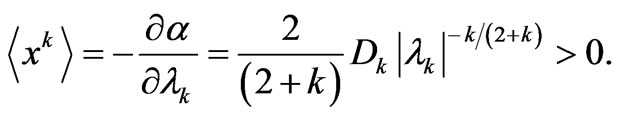 (22)
(22)
and then, using (8) one us able to build up I.
The general solution for ![]() -PDE exists. Uniqueness is, again, proved from an analysis of the associated Cauchy problem [7]. Thus, Equation (18) implies once more a kind of “universal” prescription, a linear PDE that all SE-eigenvalues must necessarily comply with.
-PDE exists. Uniqueness is, again, proved from an analysis of the associated Cauchy problem [7]. Thus, Equation (18) implies once more a kind of “universal” prescription, a linear PDE that all SE-eigenvalues must necessarily comply with.
The mathematical structure of the Legendre transform leads to a relation between the integration constants  and
and 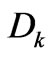 pertaining to the I and
pertaining to the I and ![]() expressions, respectively, given by (18) and (21). In [7] we studied with some detail this relation. In our two scenarios,
expressions, respectively, given by (18) and (21). In [7] we studied with some detail this relation. In our two scenarios,  and
and , we have [7]
, we have [7]
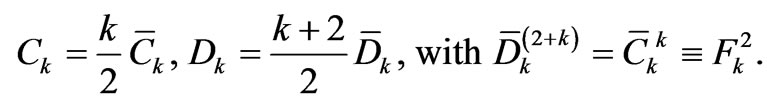 (23)
(23)
Consequently, expressions (18) and (21) take the form,
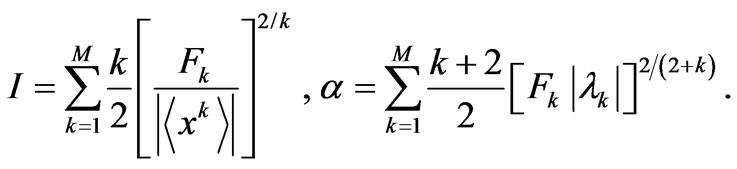 (24)
(24)
The reciprocity relations (19) and (22) can thus be economically summarized in the fashion
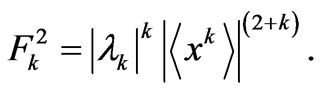 (25)
(25)
4. Present Results
4.1. The Reference Quantities Fk
The essential FIM feature is undoubtedly its being an estimation measure known to obey the Cramer Rao (CR) bound of Equation (2) [1]. Accordingly, since our partial differential equation has multiple solutions, it is natural to follow Jaynes’s MaxEnt ideas and select amongst them the one that optimizes the CR bound, that constitutes the informational operative constraint in Fisher’s instance. Of course, Jaynes needs to maximize the entropy instead. We will also, without loss of generality, renormalize the reference quantities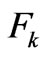 . This procedure is convenient because it allows us to regard these quantities as statistical weights that optimize the CR-bound. In other words, our procedure entails that we extremize
. This procedure is convenient because it allows us to regard these quantities as statistical weights that optimize the CR-bound. In other words, our procedure entails that we extremize
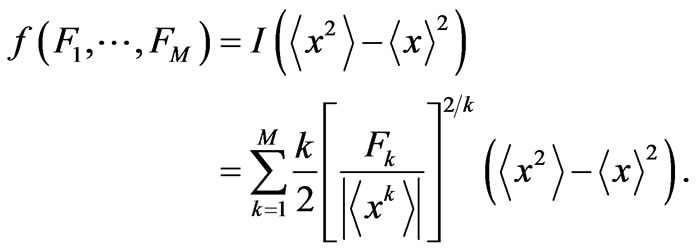 (26)
(26)
with the constraint
 (27)
(27)
We are going to apply now the preceding considerations so as to obtain the eigenvalues of the quartic anharmonic oscillator.
4.2. Quartic Anharmonic Oscillator
The Schrödinger equation for a particle of unit mass in a quartic anharmonic potential reads,
 (28)
(28)
where ![]() is the anharmonicity constant. According to [7], we can ascribe to (28) a Fisher measure and make then the following identifications:
is the anharmonicity constant. According to [7], we can ascribe to (28) a Fisher measure and make then the following identifications: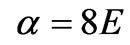 ,
,  ,
,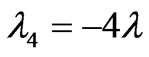 . Accordingly, we have, in the
. Accordingly, we have, in the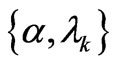 —scenario [Cf. (24)],
—scenario [Cf. (24)],
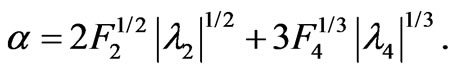 (29)
(29)
The functions f and 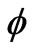 defined by (26) and (27), respectively, can here be recast [using (25)] as
defined by (26) and (27), respectively, can here be recast [using (25)] as


After these preparatory moves we can recast our methodology in a convenient specialized fashion, suitable for the task at hand. We just face the simple two-equations system:
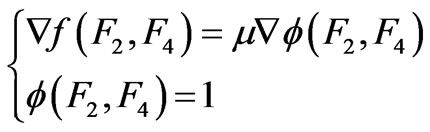 (30)
(30)
where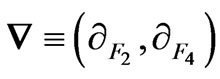 . Straightforward solution of it yields
. Straightforward solution of it yields
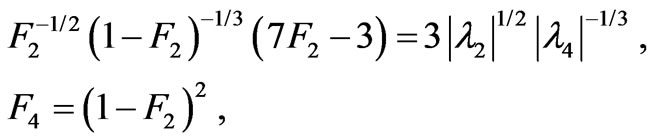 (31)
(31)
from which we obtain 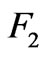 and
and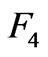 . Substituting them into (29) we determine
. Substituting them into (29) we determine ![]() and, of course, the eigenvalue
and, of course, the eigenvalue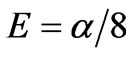 . Consider now our SE (28), taking
. Consider now our SE (28), taking 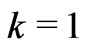 and a given value of
and a given value of ![]() (
(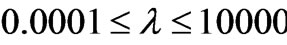 ). The function [Cf. Equation (26)]
). The function [Cf. Equation (26)] 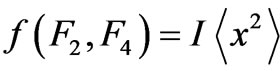 exhibits, as a function of its arguments, a unique “critical” point that satisfies (31). Using
exhibits, as a function of its arguments, a unique “critical” point that satisfies (31). Using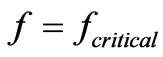 , that optimizes the CRbound, we find a ground-state eigenvalue that is in good agreement the literature. See some interesting results in Table 1.
, that optimizes the CRbound, we find a ground-state eigenvalue that is in good agreement the literature. See some interesting results in Table 1.
In this way, after properly dealing with (24), with the 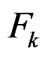 regarded as “FIM statistical weights” that optimize the Cramer Rao inequalities, we determine
regarded as “FIM statistical weights” that optimize the Cramer Rao inequalities, we determine ![]() as a function of the
as a function of the  without passing first through a Schrödinger equation, which is a notable aspect of the present approach. Interestingly enough, the Cramer-Rao inequality us equivalent to the quantum uncertainty principle (see the Appendix for details and references). Thus, our methodology actually employs Heisenberg’s celebrated principle to pick up just one solution among the several ones that our partial differential equation possesses.
without passing first through a Schrödinger equation, which is a notable aspect of the present approach. Interestingly enough, the Cramer-Rao inequality us equivalent to the quantum uncertainty principle (see the Appendix for details and references). Thus, our methodology actually employs Heisenberg’s celebrated principle to pick up just one solution among the several ones that our partial differential equation possesses.
5. Conclusions
On the basis of a variational principle based on Fisher’s information measure, free of adjustable parameters, we have obtained the Schrödinger energy-eigenvalues for the fundamental state of the quartic anharmonic oscillator (for several anharmoniticy-values). Our theoretical results, obtained without passing first through a Schrödinger equation, are in a good agreement with those of the literature. This constitutes an illustration of the power of information-related tools in analyzing physical problems.
Thus, we have in this communication introduced a new general technique for eigenvalue-problems of linear operators, whose use seems to constitute a promising
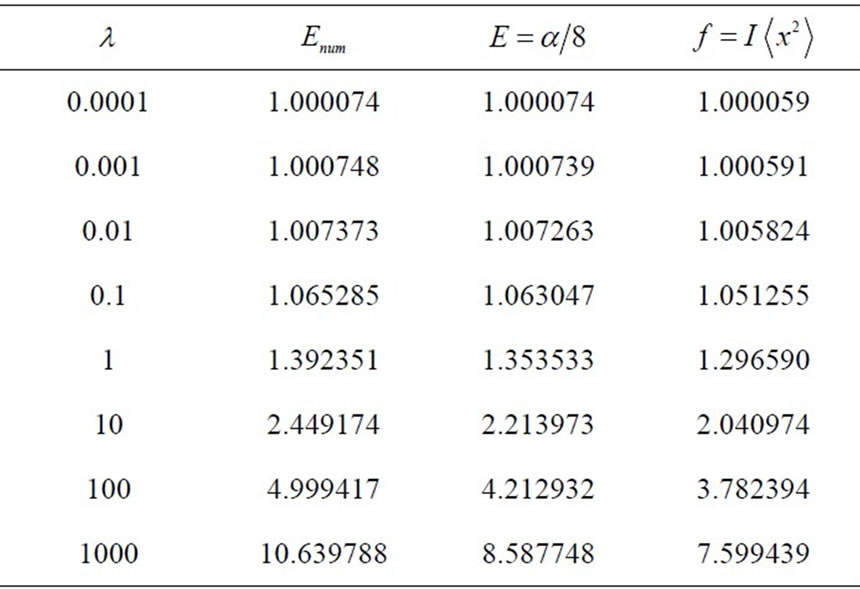
Table 1. Ground-state eigenvalues of the SE (28) for k = 1 and several values of the anharmonicity constant λ. The values of the second column correspond to those one finds in the literature, obtained via a numerical approach to the SE. These results, in turn, are nicely reproduced by some interesting theoretical approaches that, however, need to introduce and adjust some empirical constants [9]. Our values, in the third column, are obtained by means the present theoretical, parameter-free procedure. The fourth column displays the associated Cramer-Rao bound.
venue, given the results here displayed.
6. Acknowledgements
This work was partially supported by the Projects FQM- 2445 and FQM-207 of the Junta de Andalucia (Spain, EU). Acknowledges support from the Senior Grant CEI Bio-Tic GENIL-SPR.
REFERENCES
- B. R. Frieden, “Science from Fisher Information: A Unification,” Cambridge, University Press, Cambridge, 2004. doi:10.1017/CBO9780511616907
- B. R. Frieden, A. Plastino, A. R. Plastino and B. H. Soffer, “Fisher-Based Thermodynamics: Its Legendre Transform and Concavity Properties,” Physical Review E, Vol. 60, 1999, pp. 48-55. doi:10.1103/PhysRevE.60.48
- M. Reginatto, “Derivation of the Equations of Nonrelativistic Quantum Mechanics Using the Principle of Minimum Fisher Information,” Physical Review E, Vol. 58, 1998, pp. 1775-1778.
- S. P. Flego, B. R. Frieden, A. Plastino, A. R. Plastino and B. H. Soffer, “Non-Equilibrium Thermodynamics and Fisher Information: Sound Waves Propagation in a Dilute Gas,” Physical Review E, Vol. 68, No. 16, 2003, pp. 105- 115.
- S. P. Flego, A. Plastino and A. R. Plastino, “Legendretransform Structure Derived from Quantum Theorems,” Physica A, Vol. 390, 2011, pp. 2276-2281. doi:10.1016/j.physa.2011.02.019
- S. P. Flego, A. Plastino and A. R. Plastino, “Special Features of the Relation between Fisher Information and Schroedinger Eigenvalue Equation,” Journal of Mathematical Physics, Vol. 52, No. 8, 2011, pp. 2103-2116. doi:10.1063/1.3625265
- S. P. Flego, A. Plastino and A. R. Plastino, “Inferring an Optimal Fisher Measure,” Physica A, Vol. 390, 2011, pp. 4702-4712. doi:10.1016/j.physa.2011.06.050
- F. T. Hioe and E. W. Montroll, “Quantum Theory of Anharmonic Oscillators I. Energy Levels of Oscillators with Positive Quartic Anharmonicity,” Journal of Mathematical Physics, Vol. 16, 1975, pp. 1945-1950. doi:10.1063/1.522747
- C. M. Bender and T. T. Wu, “Anharmonic Oscillator,” Physical Review, Vol. 184, 1969, pp. 1231-1260. doi:10.1103/PhysRev.184.1231
- K. Banerjee, “WKB Approximation and Scaling,” Proceedings of the Royal Society A, Vol. 363, 1978, pp. 147- 151.
- R. P. Feynman, “Forces in Molecules,” Physical Review, Vol. 56, 1939, pp. 340-343.
- A. Desloge, “Thermal Physics,” Holt, Rinehart and Winston, New York, 1968.
- W. Greiner and B. Müller, “Quantum Mechanics. An Introduction,” Springer, Berlin, 1988.
- P. M. Mathews and K. Venkatesan, “A Textbook of Quantum Mechanics,” Tata McGraw-Hill Publishing Company Limited, New Delhi, 1986.
Appendix. Cramer-Rao and Uncertainty Principle
It is well known that the Cramer-Rao inequality may be regarded as an expression of Heisenberg’s Uncertainty Principle (See, for instance, [1]). Remember that a precise statement of the position-momentum uncertainty principe reads [14]
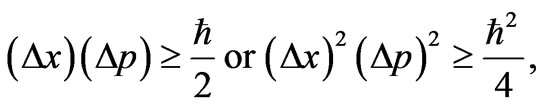 (32)
(32)
where
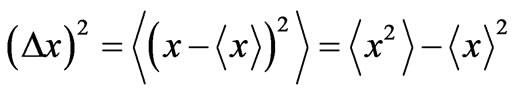 (33)
(33)
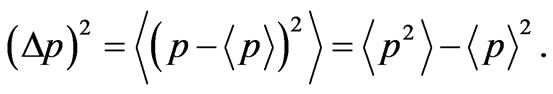 (34)
(34)
In a one-dimensional configuration-space, if 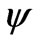 is a normalizable real wave function,
is a normalizable real wave function,
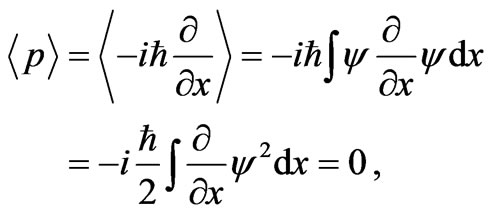 (35)
(35)
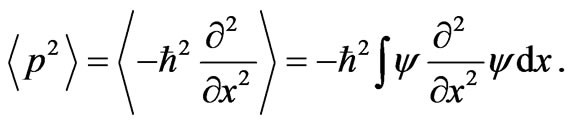 (36)
(36)
Substituting (35) and (36) in (34) and using (7) leads to the above mentioned connection between the uncertainty in momentum  and the Fisher’s measure I, i.e.,
and the Fisher’s measure I, i.e.,
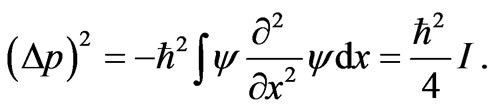 (37)
(37)
If this relation is substituted into (32) we immediately arrive to the the CR-bound,
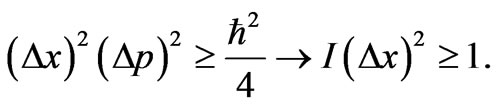 (38)
(38)
Coming now back to the  -scenario, one easily ascertains that Equation (26) can be given a clear “Heisenberg’s aspect”
-scenario, one easily ascertains that Equation (26) can be given a clear “Heisenberg’s aspect”