Journal of Modern Physics
Vol.2 No.9(2011), Article ID:7149,6 pages DOI:10.4236/jmp.2011.29128
Proposal for a Loophole-Free Bell Test with Electron Spins of Donors in Silicon
1Department of Physics, Center for Optoelectronics Materials and Devices,
Zhejiang Sci-Tech University, Hangzhou, China
2National Laboratory of Solid State Microstructures and Department of Physics, Nanjing University, Nanjing, China
3School of Physics and Electronics, Henan University, Kaifeng, China
E-mail: honghfy@163.com
Received January 3, 2011; revised May 10, 2011; accepted May 19, 2011
Keywords: Bell Inequality, Loophole-Free Test, Donor Spin, Coherent Light
ABSTRACT
So far, all experimental tests of Bell inequalities which must be satisfied by all local realistic hidden-variable theories and are violated by quantum mechanical predictions have left at least one loophole open. We propose a feasible setup allowing for a loophole-free test of the Bell inequalities. Two electron spin qubits of donors31P in a nanoscale silicon host in different cavities 300 m apart are entangled through a bright coherent light and postselections using homodyne measurements. The electron spins are then read out randomly and independently by Alice and Bob, respectively, with unity efficiency in less than 0.7 µs by using optically induced spin to charge transduction detected by radio-frequency single electron transistor. A violation of Bell inequality larger than 37% and 18% is achievable provided that the detection accuracy is 0.99 and 0.95, respectively.
1. Introduction
Most working scientists hold fast to the concepts of “realism” according to which an external reality exists independent of observation and “locality” which means that local events cannot be affected by actions in space-like separated regions [1]. The significance of these concepts goes far beyond science. Based on these deep-rooted reasonable assumptions, in their seminal 1935 paper, Einstein, Podolsky, and Rosen (EPR) advocated that quantum mechanics is incomplete [2]. The EPR arguments about the physical reality of quantum systems is shifted from the realm of philosophy to the domain of experimental physics since 1964 when Bell and others constructed mathematical inequalities—one of the profound scientific discoveries of the 20th century [3,4], which must be satisfied by any theory based on the joint assumption of realism and locality and be violated by quantum mechanics. Many experiments [1,5-12] have since been done that are consistent with quantum mechanics and inconsistent with local realism. So far, however, all these tests suffered from “loopholes” allowing a local-realistic explanation of the experimental results by exploiting either the low detector efficiency [13,14] or the timelike interval between the detection events [15,16]. The first loophole names the detection loophole allowing the possibility that the subensemble of detected events agrees with quantum mechanics even though the entire ensemble is consistent with Bell inequalities. So a fair-sampling hypothesis that the detected events represent the entire ensemble must be assumed. The second refers the locality or “lightcone” loophole allowing the correlations of apparently separate events resulting from unknown subluminal signals which propagate between space-like regions of the apparatus to take place.
Several schemes were proposed closing these loopholes based on entangled photon pairs [14,17], Hg atoms [18], Rydberg atoms [19], trapped ions [20], or non-Gaussian states of light and balanced homodyning [21,22], but all face a formidable experimental challenge. Here we discuss a scheme for the loophole-free Bell test based on the Kane Si:P architecture [23], in which two qubits are encoded onto two electron spins of donor atoms31P in nanoscale doped silicon electronic devices in two high Q cavities 300 m apart. Entanglement between the two qubits is created by using bright coherent-light pulses which interact with the donor atoms 31P through a weak dispersive light-matter interaction, respectively, via homodyne detections and postselections [24]. The qubits are then read out with perfect efficiency and high accuracy above 99% in about 0.6 µs using optically induced spin to charge transduction [25-27]. The realization of the setup is within the ability of the current semiconductor fabrication technology [28,29], and the read-out of the single donor electron spin can be realized through resonant spin-dependent charge transfer where the resulting electron current is measurable using radio-frequency single electron transistor (rf-SET) [23,25-27,30].
2. Bell Inequality Test
A Bell measurement of inequality of Clauser, Horne, Shimony, and Holt (CHSH) [4] comprises of three basic ingredients. First, a pair of particles entangled with each other is prepared in a repeatable starting configuration. Then a variable classical manipulation is applied independently and randomly to each particle; these manipulations are labeled as 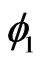 and
and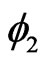 . At last, a classical property with two possible outcome values 1 and −1 is measured for each of the particles. The correlation is measured by repeating the experiment many times and can be expressed as
. At last, a classical property with two possible outcome values 1 and −1 is measured for each of the particles. The correlation is measured by repeating the experiment many times and can be expressed as
 (1)
(1)
where 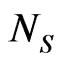 and
and  denote the numbers of measurements in which the measured results are the same or different, respectively. The CHSH form of Bell inequalities states that the correlations resulting from local realistic theories must satisfy:
denote the numbers of measurements in which the measured results are the same or different, respectively. The CHSH form of Bell inequalities states that the correlations resulting from local realistic theories must satisfy:
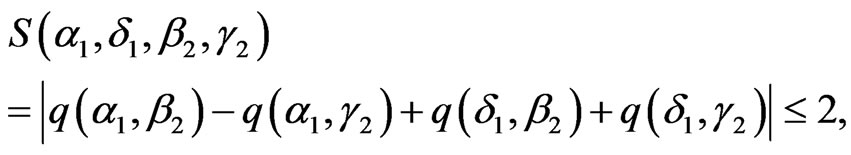 (2)
(2)
where  and
and  (
(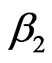 and
and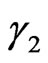 ) are specific values of
) are specific values of 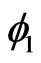 (
(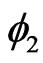 ). For a Bell measurement based on electron spins, we have
). For a Bell measurement based on electron spins, we have
 (3)
(3)
where 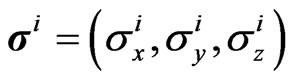 with
with  (i = A, B, and
(i = A, B, and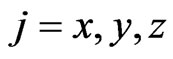 ) being the Pauli matrices, and
) being the Pauli matrices, and  (
(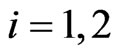 ) are unit vectors. The CHSH inequality (2) is maximally violated by quantum mechanics at certain sets of
) are unit vectors. The CHSH inequality (2) is maximally violated by quantum mechanics at certain sets of  and
and , one such set is that both of the
, one such set is that both of the 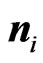 (
( ) are in the xy-plane, and the polar angles of
) are in the xy-plane, and the polar angles of 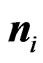 (
(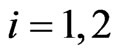 ) are
) are ,
, 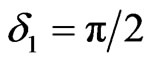 for
for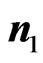 , and
, and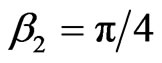 ,
,  for
for . For these phase angles and state
. For these phase angles and state
 , the quantum mechanics gives
, the quantum mechanics gives
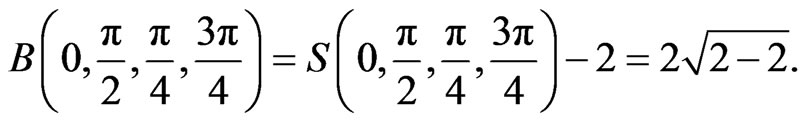 (4)
(4)
The architecture of the basic phosphorus 31P donor electron spin qubit in silicon with control gates and a resonant readout mechanism are shown in Figure 1. The donors serve to localize the electron spins in space which encode quantum information in the conventional fashion as  and
and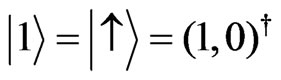 , and to provide local qubit addressability through the electron nuclear hyperfine interaction [23]. Indirect spin detection involves transfer of the spin information to the charge degrees of freedom through a spin-dependent tunneling process, during which the resulting electron current can be detected by an ultrasensitive electrometer, rf-SET [25]. This concept depends on the application of a small dc electric field
, and to provide local qubit addressability through the electron nuclear hyperfine interaction [23]. Indirect spin detection involves transfer of the spin information to the charge degrees of freedom through a spin-dependent tunneling process, during which the resulting electron current can be detected by an ultrasensitive electrometer, rf-SET [25]. This concept depends on the application of a small dc electric field 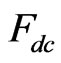 and an ac electric field
and an ac electric field 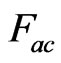 with the amplitude
with the amplitude 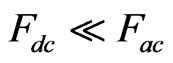 resonant at the energy gap
resonant at the energy gap 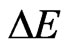 of the two states
of the two states  and
and  to induce the tunneling of the qubit electron to a secondary (spin polarized) “SET-donor”. Here
to induce the tunneling of the qubit electron to a secondary (spin polarized) “SET-donor”. Here 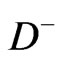 denotes the state with two electrons being bound to the same donor formed by the tunneling. The resulting charge re-distribution can be detected by a rf-SET. This detection is equivalent to the measurement of the qubit spin state, because the tunneling event
denotes the state with two electrons being bound to the same donor formed by the tunneling. The resulting charge re-distribution can be detected by a rf-SET. This detection is equivalent to the measurement of the qubit spin state, because the tunneling event  will be Pauli blocked if the qubit and the SET-donor electron spins are parallel.
will be Pauli blocked if the qubit and the SET-donor electron spins are parallel.
To generate entanglement between donor qubits at Alice’s and Bob’s sites 300 m apart, a bright coherent pulse sequentially interacts with the qubits, entangled qubit pairs will then be postselected conditioned upon the results of probe homodyne measurements. For a sufficient dispersive interaction between the donor electron and the light, the system should be placed in a cavity resonant with the light. For the cavity, weak coupling is
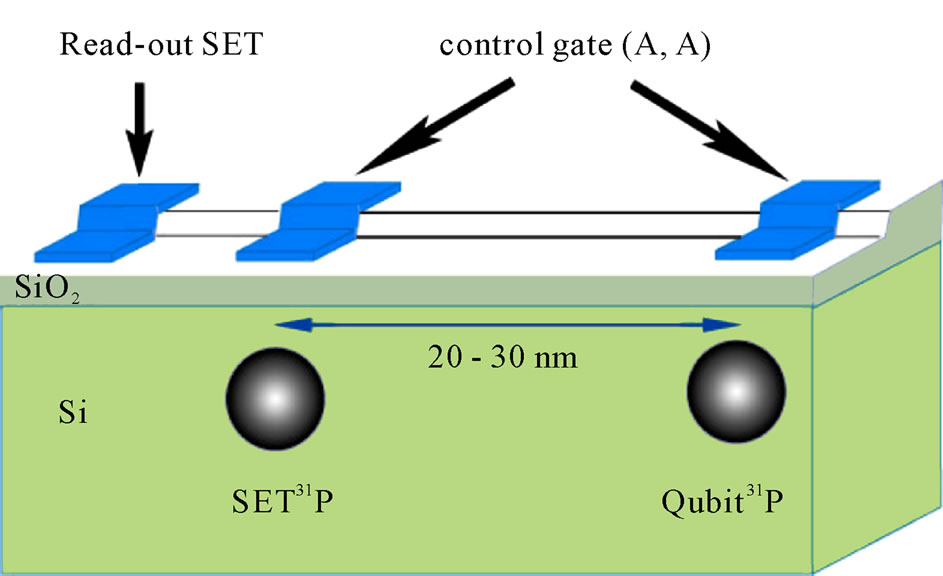
Figure 1. (Color online) Schematic picture of the device for the resonant spin-dependent charge transfer of a single electron of a donor 31P in silicon. The tunneling event D0D0 ® D+D– is Pauli blocked if the qubit donor and the SET-donor spins are parallel.
sufficient, but a high value of  is required, where Q is the quality and V is the mode-volume of the cavity [24].
is required, where Q is the quality and V is the mode-volume of the cavity [24].
The donor electron spin system in the cavity is treated as a 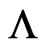 system with two stable and metastable ground states
system with two stable and metastable ground states 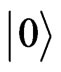 and
and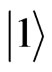 , and an excited state
, and an excited state 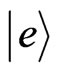 provided by the bound-exciton state. For the coherent pulses, the transition between
provided by the bound-exciton state. For the coherent pulses, the transition between 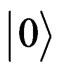 and
and 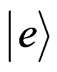 is suppressed due to a prohibitive selection rule and only
is suppressed due to a prohibitive selection rule and only  and
and  participate in the interaction with the cavity mode [31]. Assuming that the state of the qubits in Alice’s and Bob’s sites are initially prepared in the states
participate in the interaction with the cavity mode [31]. Assuming that the state of the qubits in Alice’s and Bob’s sites are initially prepared in the states  and
and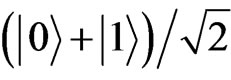 , respectively, and the two SET 31P are in
, respectively, and the two SET 31P are in  state that makes them not to take part in the interaction with the bright coherent pulses. The coherent light is sufficiently detuned from the transition between
state that makes them not to take part in the interaction with the bright coherent pulses. The coherent light is sufficiently detuned from the transition between  and the excited state to allow for a strictly dispersive light-matter interaction. When the probe pulse in coherent state
and the excited state to allow for a strictly dispersive light-matter interaction. When the probe pulse in coherent state  reflects from the cavity at the Alice’s sitethe total output state may be described by [24]
reflects from the cavity at the Alice’s sitethe total output state may be described by [24]
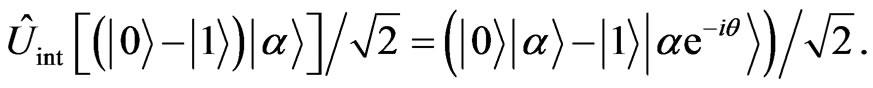 (5)
(5)
The probe beam is then sent to the cavity at the Bob’s site and interacts with the qubit donor in the same way. Applying a further linear phase shift of θ to the pulse after it leaves the cavity will yield the total state
 (6)
(6)
where 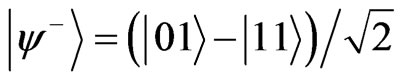 with the conventional denotation
with the conventional denotation  and
and  hereafter. In the presence of channel loss, we may model the photon loss by considering a beam splitter in the channel that transmits only a part of the probe pulse with transmission
hereafter. In the presence of channel loss, we may model the photon loss by considering a beam splitter in the channel that transmits only a part of the probe pulse with transmission  [24]. Tracing over the lost photons introduces decoherence and the total state can be described by density matrix ρ, with the following diagonal part for the pulse states
[24]. Tracing over the lost photons introduces decoherence and the total state can be described by density matrix ρ, with the following diagonal part for the pulse states
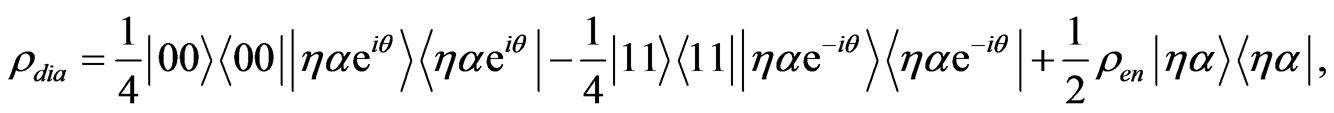 (7)
(7)
where
 (8)
(8)
Here 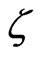 is the decoherence factor arising from the dispersive light-matter interaction in the cavities,
is the decoherence factor arising from the dispersive light-matter interaction in the cavities,
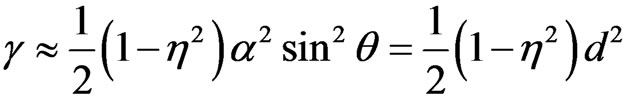 , and an extra phase
, and an extra phase
 can be set to be naught, since it is independent of the measurement results and can be locally removed via static phase shifters.
can be set to be naught, since it is independent of the measurement results and can be locally removed via static phase shifters.
With the balanced homodyne detection [32], the success probability of generating entanglement between two qubits at Alice’s and Bob’s sites is found to be [24]
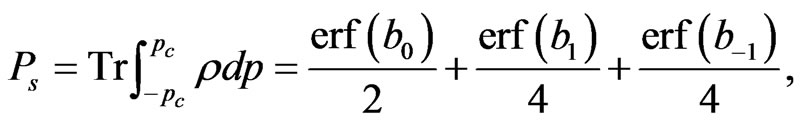 (9)
(9)
where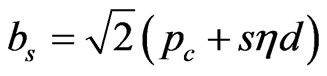 ,
, 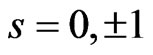 , and
, and 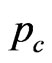 is the selection window of the homodyne measurements. The desired entangled output state is
is the selection window of the homodyne measurements. The desired entangled output state is , so the average fidelity after postselection has the form [24]
, so the average fidelity after postselection has the form [24]
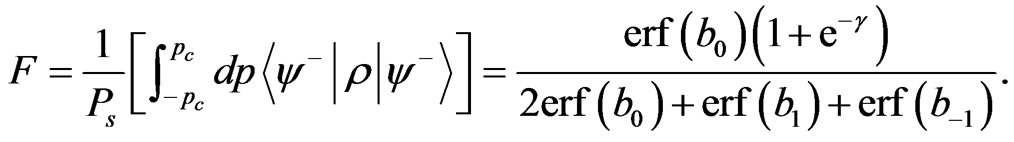 (10)
(10)
For the state obtained through the postselection with the configuration for  (
( ) aforesaid, the violation of the CHSH inequalities reads
) aforesaid, the violation of the CHSH inequalities reads
 (11)
(11)
After the pulse leaves the cavity at the Bob’s site, Alice and Bob randomly and dependently manipulate the electron spins of the SET 31P from the initial state 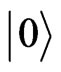 to the state
to the state  corresponding to
corresponding to  or the state
or the state 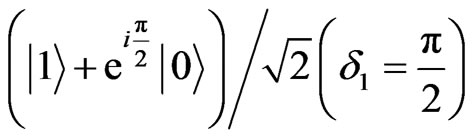 and to state
and to state
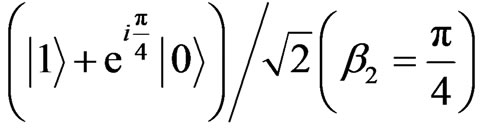 or the state
or the state
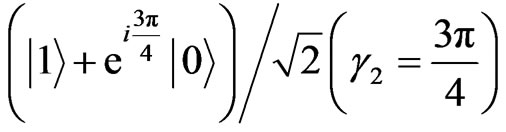 , respectively. These manipulations on the SET 31P electron spins equivalent to the actions on the qubit donor spins can be finished in 0.1 µs [33]. Then Alice and Bob read out the electron spins of the qubit 31P using optically induced spin to charge transduction detected by the rf-SET. If the qubit and SET-donor electron spins are parallel, the tunneling event
, respectively. These manipulations on the SET 31P electron spins equivalent to the actions on the qubit donor spins can be finished in 0.1 µs [33]. Then Alice and Bob read out the electron spins of the qubit 31P using optically induced spin to charge transduction detected by the rf-SET. If the qubit and SET-donor electron spins are parallel, the tunneling event 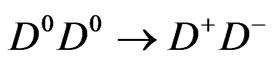 will be Pauli blocked, thus the rf-SET will detect nothing, which will be assigned a value +1. Otherwise, the rf-SET will detect a current signal, and the outcome will be assigned –1. The outcomes of every experiment can be used to compute the correlation function
will be Pauli blocked, thus the rf-SET will detect nothing, which will be assigned a value +1. Otherwise, the rf-SET will detect a current signal, and the outcome will be assigned –1. The outcomes of every experiment can be used to compute the correlation function , so that fair-sampling hypothesis is not required. In this case, the issue of the detection efficiency is replaced by the detection accuracy
, so that fair-sampling hypothesis is not required. In this case, the issue of the detection efficiency is replaced by the detection accuracy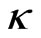 . The main origin of the inaccuracy in the detection of electron spins comes from the imperfection in the spin to charge transduction, i.e., the tunneling event
. The main origin of the inaccuracy in the detection of electron spins comes from the imperfection in the spin to charge transduction, i.e., the tunneling event 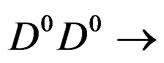
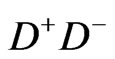 may not happen even if the qubit and SET-donor electron spins are antiparallel. This leads to an experimental result that the probability of the qubit spin parallel to the SET-donor spin will be larger than that obtained with the perfect detection accuracy. The read-out of the qubit spin with the detection accuracy
may not happen even if the qubit and SET-donor electron spins are antiparallel. This leads to an experimental result that the probability of the qubit spin parallel to the SET-donor spin will be larger than that obtained with the perfect detection accuracy. The read-out of the qubit spin with the detection accuracy  may be possible according to [27,30]. Considering the detection accuracy
may be possible according to [27,30]. Considering the detection accuracy  and the detection error rate
and the detection error rate , the violation of the CHSH inequalities B in Equation (11) may be rewritten as
, the violation of the CHSH inequalities B in Equation (11) may be rewritten as
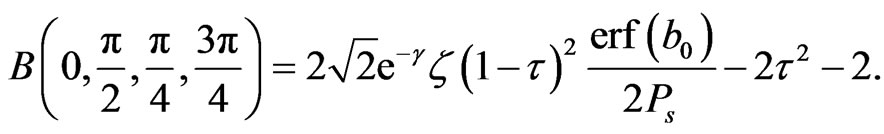 (12)
(12)
Assuming the telecom fiber and wavelength where losses are about 1 dB/km [34], the transmission parameter of 300 m is . For 31P donor impurity in silicon, distinguishability of
. For 31P donor impurity in silicon, distinguishability of  corresponding to
corresponding to 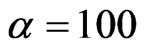 and
and  is achievable [31]. Assuming that the decoherence factor
is achievable [31]. Assuming that the decoherence factor 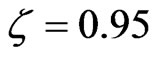 and the detection accuracy
and the detection accuracy , from Equations (9), (10) and (12), we obtain the results shown in Figure 2. Assuming that the selection window
, from Equations (9), (10) and (12), we obtain the results shown in Figure 2. Assuming that the selection window 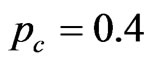 and other parameters unchanged, we get the relation between the violation of the CHSH inequalities B and the detection accuracy
and other parameters unchanged, we get the relation between the violation of the CHSH inequalities B and the detection accuracy  as shown in Figure 3. When
as shown in Figure 3. When 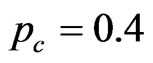 and
and , we have
, we have ,
, 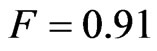 and
and . Even the detection accuracy is so low that
. Even the detection accuracy is so low that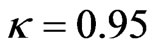 , we still have
, we still have 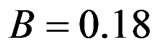 for
for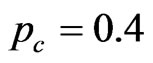 . With a repetition rate of 500 kHz and
. With a repetition rate of 500 kHz and , the number of data samples would be 150,000 per second, thus the whole Bell test experiments would be finished in less than one second.
, the number of data samples would be 150,000 per second, thus the whole Bell test experiments would be finished in less than one second.
Building the setup shown in Figure 1 is within the reach of the current technology. The two donors of distance 20 - 30 nm can be placed through random doping techniques, though only a small percentage of such devices will work properly [23]. The three gates with lateral dimensions and separation ~10 nm can be patterned on the surface through technologies such as self-assembly and the use of extreme ultraviolet radiation, x-rays, and electron beams [28,35]. A workable transistor with a gate length of 6 nm has already been realized in 2002 [28]. The two qubit states have an energy split 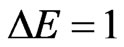 meV for an applied 8.6 T magnetic field. The exited state
meV for an applied 8.6 T magnetic field. The exited state 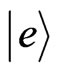 is about 1.09 eV above the ground state [36]. The probe coherent pulses of wavelength about 1650 nm (
is about 1.09 eV above the ground state [36]. The probe coherent pulses of wavelength about 1650 nm (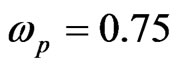 eV) (Figure 4) are far detuned from the transition
eV) (Figure 4) are far detuned from the transition , but on resonant with the cavity with frequency
, but on resonant with the cavity with frequency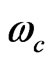 , of which the device of dimensions about 50 nm × 30 nm × 30 nm is at the antinode [31].
, of which the device of dimensions about 50 nm × 30 nm × 30 nm is at the antinode [31].
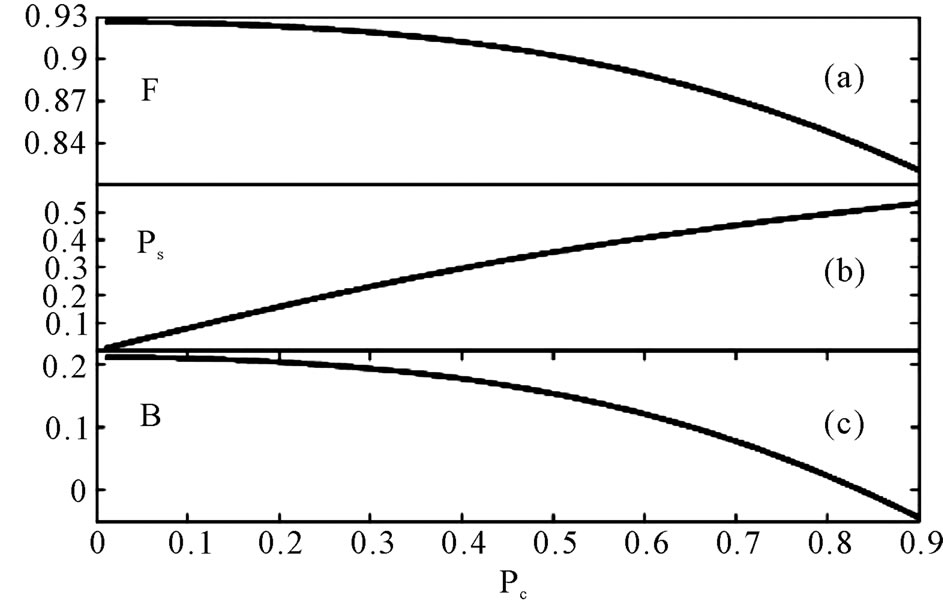
Figure 2. The fidelity of the obtained state by postselection (a), the success probability Ps (b), and the violation of the CHSH inequalities  (c) as functions of the postselection window
(c) as functions of the postselection window  in the case of the detection accuracy
in the case of the detection accuracy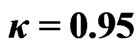 . See the text for the values of other parameters.
. See the text for the values of other parameters.
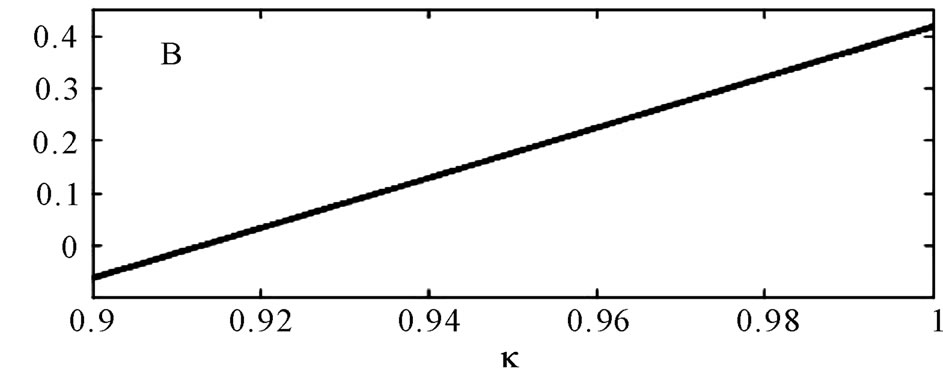
Figure 3. The violation of the CHSH inequalities
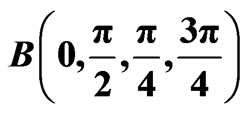 versus the detection accuracy
versus the detection accuracy 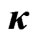 with
with . See the text for the values of other parameters.
. See the text for the values of other parameters.

Figure 4. The schematic of relevant energy structure of a phosphorous impurity in silicon, probe pulses, and the cavity. The probe pulses are on resonant with the cavity, 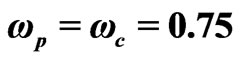 eV, and far detuned from the atomic transition
eV, and far detuned from the atomic transition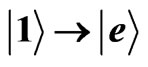 . Energy split
. Energy split 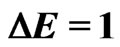 meV for an applied 8.6 T magnetic field. The energy difference between
meV for an applied 8.6 T magnetic field. The energy difference between 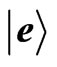 and
and 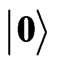 is about 1.09 eV.
is about 1.09 eV.
3. Conclusions
As a summary, we present a scheme for the loopholefree test of the Bell inequalities. The detection efficiency of donor electron spins is unity using the optically induced spin to charge transfer detected by a rf-SET, and the fair sampling assumption is not required, thereby the detection loophole in this scheme is closed. The two qubit donors are 300 m apart, and the time of the random and independent measurement of the two qubits by Alice and Bob, respectively, is within 0.7 µs, thus the lightcone loophole may be closed too. The experimental realization of this scheme is within the reach of the current technology. Large violation of the CHSH inequality  for the detection accuracy
for the detection accuracy  is achievable. Even if the detection accuracy is so low that
is achievable. Even if the detection accuracy is so low that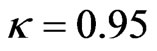 , we may still have
, we may still have . This scheme may open a promising avenue towards a complete experimental Bell test which has a profound significance far beyond science.
. This scheme may open a promising avenue towards a complete experimental Bell test which has a profound significance far beyond science.
4. Acknowledgements
This work was supported by the National Nature Science Foundation of China (Grant No.10874071, 50672088, 11072218, 11005031, and 60571029), by Zhejiang Provincial Natural Science Foundation of China (Grant No. Y6110314), by Scientific Research Fund of Zhejiang Provincial Education Department (Grant No.Y200909693), and by Science Foundation of Zhejiang Sci-Tech University (ZSTU) under Grant No.0913842-Y.
REFERENCES
- J. F. Clauser and A. Shimony, “Bell’s Theorem. Experimental Tests and Implications,” Reports on Progress in Physics, Vol. 41, No. 12, 1978, pp. 1863-1883. doi:10.1088/0034-4885/41/12/002
- A. Einstein, B. Podolsky and N. Rosen, “Can Quantum Mechanical Description of Physical Reality Be Considered Complete?” Physical Reviews, Vol. 47, No. 10, 1935, pp. 777-780. doi:10.1103/PhysRev.47.777
- J. S. Bell, “On the Einstein Podolsky Rosen Paradox,” Physics, Vol. 1, No. 3, 1964, pp. 195-200.
- J. F. Clauser, M. A. Horne, A. Shimony and R. A. Holt, “Proposed Experiment to Test Local Hidden-Variable Theories,” Physical Review Letters, Vol. 23, No. 15, 1969, pp. 880-884. doi:10.1103/PhysRevLett.23.880
- S. J. Freedman and J. F. Clauser, “Experimental Test of Local Hidden-Variable Theories,” Physical Review Letters, Vol. 28, No. 14, 1972, pp. 938-941. doi:10.1103/PhysRevLett.28.938
- E. S. Fry and R. C. Thompson, “Experimental Test of Local Hidden-Variable Theories,” Physical Review Letters, Vol. 37, No. 8, 1976, pp. 465-468. doi:10.1103/PhysRevLett.37.465
- A. Aspect, P. Grangier and G. Roger, “Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedanken Experiment: A New Violation of Bell’s Inequalities,” Physical Review Letters, Vol. 49, 1982, p. 91. doi:10.1103/PhysRevLett.49.91
- Z. Y. Ou and L. Mandel, “Violation of Bell’s Inequality and Classical Probability in a Two-Photon Correlation Experiment,” Physical Review Letters, Vol. 61, No. 1, 1988, pp. 50-53. doi:10.1103/PhysRevLett.61.50
- P. R. Tapster, J. G. Rarity and P. C. M. Owens, “Violation of Bell’s Inequality over 4 km of Optical Fiber,” Physical Review Letters, Vol. 73, No. 14, 1994, pp. 1923- 1926. doi:10.1103/PhysRevLett.73.1923
- P. G. Kwiat, K. Mattle, H. Weinfurter and A. Zeilinger, “New High-Intensity Source of Polarization-Entangled Photon Pairs,” Physical Review Letters, Vol. 75, No. 24, 1995, pp. 4337-4341. doi:10.1103/PhysRevLett.75.4337
- W. Tittel, J. Brendel, H. Zbinden and N. Gisin, “Violation of Bell Inequalities by Photons More Than 10 km Apart,” Physical Review Letters, Vol. 81, No. 17, 1998, pp. 3563-3566. doi:10.1103/PhysRevLett.81.3563
- M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe and D. J. Wineland, “Experimental Violation of a Bell’s Inequality with Efficient Detection,” Nature, Vol. 409, 2001, pp. 791-794.
- P. M. Pearle. “Hidden-Variable Example Based upon Data Rejection,” Physics Review D, Vol. 2, No. 8, 970, pp. 1418-1425.
- E. Santos, “Critical Analysis of the Empirical Tests of Local Hidden-Variable Theories,” Physical Review A, Vol. 46, No.7, 1992, pp. 3646-3656. doi:10.1103/PhysRevA.46.3646
- J. S. Bell, “Speakable and Unspeakable in Quantum Mechanics,” Cambridge University Press, Cambridge, 1988.
- E. Santos, “Constraints for the Violation of the Bell Inequality in Einstein-Podolsky-Rosen -Bohm Experiments,” Physical Review A, Vol. 200, 1995, p. 1.
- S. F. Huelga, M. Ferrero and E. Santos, “Atomic-Cascade Experiment with Detection of the Recoil Atom,” Europhysics Letters, Vol. 27, No. 3, 1994, p. 181.
- E. S. Fry, T. Walther and S. Li, “Proposal for a Loophole Free Test of the Bell Inequalities,” Physical Review A, Vol. 52, No. 6, 1995, pp. 4381-4395. doi:10.1103/PhysRevA.52.4381
- M. Freyberger, et al., “Proposed Test of Bells Inequality without a Detection Loophole by Using Entangled Rydberg Atoms,” Physical Review A, Vol. 53, No. 3, 1996, pp. 1232-1244. doi:10.1103/PhysRevA.53.1232
- C. Simon and W. T. M. Irvine, “Robust Long-Distance Entanglement and a Loophole-Free Bell Test with Ions and Photons,” Physical Review Letters, Vol. 91, No. 11, 2003, pp. 1-4. doi:10.1103/PhysRevLett.91.110405
- H. Nha and H. J. Carmichael, “Proposed Test of Quantum Nonlocality for Continuous Variables,” Physical Review Letters, Vol. 93, No. 2, 2004, Article ID: 020401. doi:10.1103/PhysRevLett.93.020401
- R. Garcia-Patron, J. Fiurasek, N. J. Cerf, J. Wenger, R. Tualle-Brouri and P. Grangier, “Proposal for a Loophole-Free Bell Test Using Homodyne Detection,” Physical Review Letters, Vol. 93, No. 13, 2004, Article ID: 130409.
- B. E. Kane, “A Silicon-Based Nuclear Spin Quantum Computer,” Nature, Vol. 393, No. 6681, 1998, pp. 133- 137.
- P. van Loock, T. D. Ladd, K. Sanaka, F. Yamaguchi, K. Nemoto, W. J. Munro and Y. Yamamoto, “Hybrid Quantum Repeater Using Bright Coherent Light,” Physical Review Letters, Vol. 96, 2006, Article ID: 240501. doi:10.1103/PhysRevLett.96.240501
- R. J. Schoelkopf, P. Wahlgren, A. A. Kozhevnikov, P. Delsing and D. E. Prober, “The Radio-Frequency Single-Electron Transistor (RF-SET): A Fast and Ultrasensitive Electrometer,” Science, Vol. 280, No. 5367, 1998, pp. 1238-1242.
- T. M. Buehler, D. J. Reilly, R. P. Starrett, A. D. Greentree, A. R. Hamilton, A. S. Dzurak and R. G. Clark, “Single-Shot Readout with the Radio-Frequency Single- Electron Transistor in the Presence of Charge Noise,” Applied Physics Letters, Vol. 86, No. 14, 2005, Article ID: 143117. doi:10.1063/1.1897423
- M. J. Testolin, A. D. Greentree, C. J. Wellard and L. C. L. Hollenberg, “Optically Induced Spin-to-Charge Transduction in Donor-Spin Readout,” Physical Review B, Vol. 72, No. 19, 2005, Article ID: 195325. doi:10.1103/PhysRevB.72.195325
- M. Leong, B. Doris, J. Kedzierski, K. Rim and M. Yang, “Silicon Device Scaling to the Sub-10-nm Regime,” Science, Vol. 306, No. 5704, 2004, pp. 2057-2060.
- M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L. W. Molenkamp, X.-L. Qi and S.-C. Zhang, “Quantum Spin Hall Insulator State in HgTe Quantum Wells,” Science, Vol. 318, No. 5851, 2007, pp. 766-770.
- L. C. L Hollenberg, C. J. Wellard, C. I. Pakes and A. G. Fowler, “Single-Spin Readout for Buried Dopant Semiconductor Qubits,” Physical Review B, Vol. 69, No. 23, 2004, Article ID: 233301. doi:10.1103/PhysRevB.69.233301
- T. D. Ladd, P. van Loock, K. Nemoto, W. J. Munro and Y. Yamamoto, “Hybrid Quantum Repeater Based on Dispersive CQED Interactions between Matter Qubits and Bright Coherent Light,” New Journal of Physics, Vol. 8, 2006, p. 184. doi:10.1088/1367-2630/8/9/184
- M. O. Scully and M. S. Zubairy, “Quantum Optics,” Cambridge, 1997.
- C. D. Hill, L. C. L. Hollenberg, A. G. Fowler, C. J. Wellard, A. D. Greentree and H.-S. Goan, “Global Control and Fast Solid-State Donor Electron Spin Quantum Computing,” Physical Review B, Vol. 72, No. 4, 2005, Article ID: 045350. doi:10.1103/PhysRevB.72.045350
- N. Gisin, G. Ribordy, W. Tittel and H. Zbinden, “Quantum Cryptography,” Reviews of Modern Physics, Vol. 74, 2002, pp. 145-195. doi:10.1103/RevModPhys.74.145
- O. Guise, J. T. Yates Jr. and J. Levy, “Patterning of Sub-10-nm Ge islands on Si(100) by Directed Self-Assembly,” Applied Physics Letters, Vol. 87, No. 17, 2005, Article ID: 171902. doi:10.1063/1.2112198
- D. Karaiskaj, M. L. W. Thewalt, T. Ruf, M. Cardona, H.-J. Pohl, G. G. Deviaych, P. G. Sennikov and H. Riemann, “Photoluminescence of Isotopically Purified Silicon: How Sharp Are Bound Exciton Transitions?” Physical Review Letters, Vol. 86, No. 26, 2001, pp. 6010-6013. doi:10.1103/PhysRevLett.86.6010

