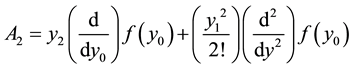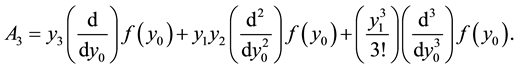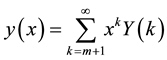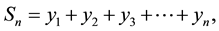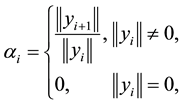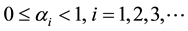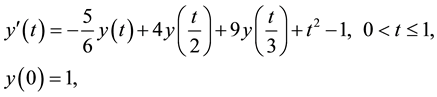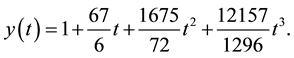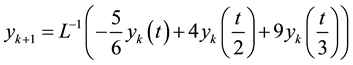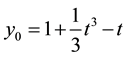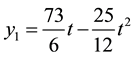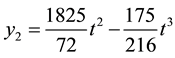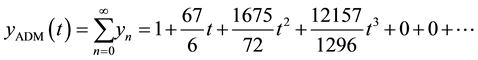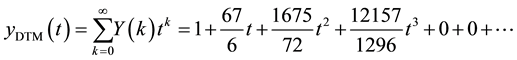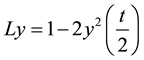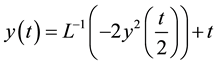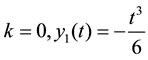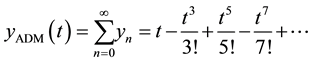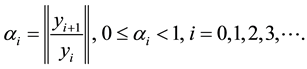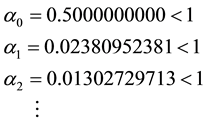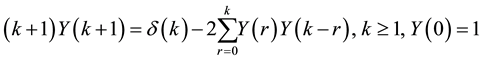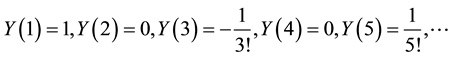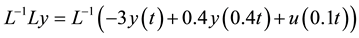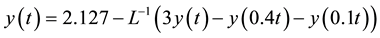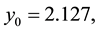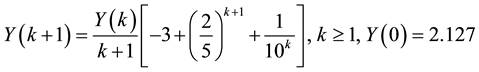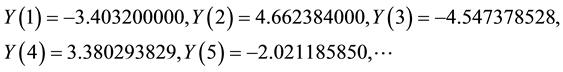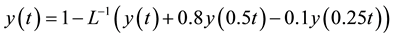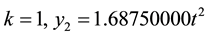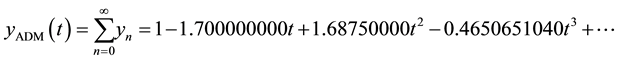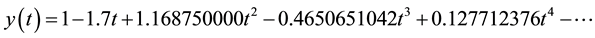Applied Mathematics
Vol.06 No.08(2015), Article ID:58318,11 pages
10.4236/am.2015.68126
The Adomian Decomposition Method and the Differential Transform Method for Numerical Solution of Multi-Pantograph Delay Differential Equations
Musa Cakir, Derya Arslan
Department of Mathematics, Faculty of Science, University of Yuzuncu Yil, Van, Turkey
Email: cakirmusa@hotmail.com, ayredlanu@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 May 2015; accepted 24 July 2015; published 27 July 2015
ABSTRACT
In this paper, the Adomian Decomposition Method (ADM) and the Differential Transform Method (DTM) are applied to solve the multi-pantograph delay equations. The sufficient conditions are given to assure the convergence of these methods. Several examples are presented to demonstrate the efficiency and reliability of the ADM and the DTM; numerical results are discussed, compared with exact solution. The results of the ADM and the DTM show its better performance than others. These methods give the desired accurate results only in a few terms and in a series form of the solution. The approach is simple and effective. These methods are used to solve many linear and nonlinear problems and reduce the size of computational work.
Keywords:
Multi-Pantograph Delay Differential Equations, Adomian Decomposition Method (ADM), Differential Transform Method (DTM), Convergence of Adomian Decomposition Method

1. Introduction
Pantograph is a device located on the electriclocomotive. The first time, electric locomotive was made in America in 1851. It was commissioned in 1895. Mathematical model of pantograph was first developed by Taylor and Ockendon (1971) [1] . Pantograph equations belong to a special class of functional-differential equations with proportional delays and arise in many applications such as, astrophysics, nonlinear dynamical systems, probabi- lity theory on algebraic structures, electro dynamics, quantum mechanics and cell growth, number theory, mixing problems, population models, etc.
In recent years, the multi-pantograph delay differential equations were studied by many authors. For examples, Li and Liu [2] applied the Runge-Kutta methods to the multi-pantograph delay equation. Evans and Raslan [3] used the Adomian decomposition method for solving the delay differential equation. Keskin et al. [4] applied the differential transform method to obtain the approximate solution. Sezer and Dascioglu [5] developed and applied the Taylor method to the generalized pantograph equation with retarded case or advanced case. Brunner [1] used the collocation methods for pantograph-type Volterra functional equations with multiple delays. Yu [6] applied the variational iteration method to the multi-pantograph delay equation. Sezer et al. [7] worked approxi- mate solution of multi-pantograph equation with variable coefficients. Geng, F. Z. and Qian, S. P. [8] worked the Reprociding Kernel Medhod to Solving Singularly Perturbed Multi-Pantograph Delay Equations. Cherruault, Y., Adomian, G., Abbaoui, K. and Rach, R. [9] worked on Convergence of Decomposition Method. Ismail et al. [10] gave the numerical solutions of the Korteweg-De-Vries (KDV) and modified Korteweg-De-Vries Equations. El-Safty et al. [11] studied on the 3-h step spline function approximation to the solution of delay dynamic system. Saeed and Rahman [12] established the differential transform method to solve systems of linear or non-linear delay differential equation.
A numerical method based on the Adomian Decomposition Method (ADM) which has been used from the 1970s to the 1990s by George Adomian [13] [14] . The differential transform method (DTM) has been successfully developed by Zhou (1986) in electric circuit analysis. DTM has been used to solve linear and nonlinear differential equations [15] .
ADM and DTM have been shown to solve effectively, easily and accurately a large class of linear and nonlinear, ordinary, partial, deterministic or stochastic differential equations with approximate solutions which converge rapidly to accurate solutions [3] [4] [13] [14] . The basic motivation of this work is to apply the ADM and DTM to the DDE. It is well known now in the literature that this algorithm provides the solution in a rapidly convergent series [3] [4] . ADM and DTM are very effective and convenient for solving multi-pantograph equations [3] [4] .
This study is presented as follows: In second section, we start by presenting ADM and DTM to solve multi-pantograph delay differential equations. In third section, we continue to the presentation of the convergence of ADM with Theorem 3.1 and Definition 3.2. In fourth section, these methods are shown and compared by four examples by taking various values for t and error evaluation is made. Also, we have plotted the graphs for numerical solutions of ADM and DTM and exact solution.
We examined that multi-pantograph delay differential equations are solved by several methods. Thus, we wanted to show up that may be more efficient, simpler and reliable the solution treatment of the ADM for multi- pantograph delay differential equations. The results show that the ADM is more powerful method than other methods for multi-pantograph delay differential equations.
2. Analysis of Adomian Decomposition Method and the Differential Transform
In this paper, we consider the following multi-pantograph equations [16] ,
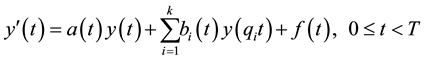 (1)
(1)
 (2)
(2)
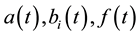 are analytical functions,
are analytical functions,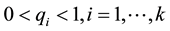 .
.
Using the ADM, the differential operator L is given by
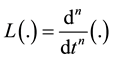 (3)
(3)
The inverse operator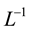 , this is n-fold integral operator defined by
, this is n-fold integral operator defined by
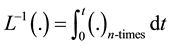 (4)
(4)
operating with 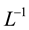 on Equation (1), it then follows
on Equation (1), it then follows
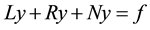 (5)
(5)
where the method defines 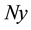 the nonlinear term by the Adomian polynomials [3] [13] [14]
the nonlinear term by the Adomian polynomials [3] [13] [14]

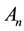 are Adomian polynomials that can be generated for all forms of nonlinearity as
are Adomian polynomials that can be generated for all forms of nonlinearity as
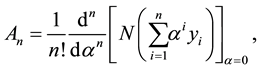
where 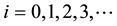
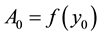
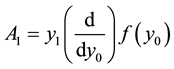
Operating with 

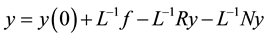
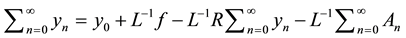
to determine the components
First, we identify the zero component 


and Equation (8) gives for 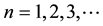

The Adomian decomposition method assumes that the unknown function 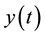
so that the components 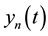
Differential Transform Method
Differential transform of function 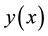

In Equation (11), 


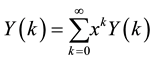
From Equations (12) and (11), we obtain

Equation (13) implies that concept of differential transform is derived from Taylor series expansion, but the method does not evaluate the derivatives symbolically.
In actual applications, the function 

Equation (13) implies that is
is negligibly small. In fact, m is decided by the convergence of natural frequency in this study.
The following theorems that can be deduced from Equations (11) and (12) are given below, see [17] [18] .
Theorem 1 If
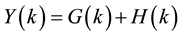
Theorem 2 If

Theorem 3 If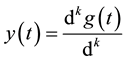

Theorem 4 If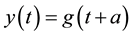

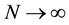
Theorem 5 If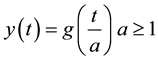
3. The Convergence of ADM
The Adomian Decomposition Method is equivalent to the sequence defined as follows [19] [20]
by using the iterative scheme

and related to the functional equation
The numerical solution of Equation (15) was used fixed-point theorem by Cherruault [19] [20] .
Theorem 3.1 Let N be an operator from Hilbert space H in to H and y be the exact solution of functional equation.

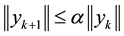

Proof See [19] [20] .
Definition 3.2 For every 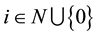
Corollary 3.3 In Theorem 4.1, 
4. Numerical Examples
In this section, four experiments of multi-pantograph delay differential equations are given to illustrate the efficiency of the ADM and the DTM. The examples are computed using Maple 15. Results obtained by the methods are compared with the exact solution of each example and found to be good agreement with each other. The absolute errors in tables are given at selected points.
Example 4.1 Consider the following linear multi-pantograph delay equation of the first-order [16]
which has the exact solution,
Using the ADM, we get according to Equations (3)-(10), we obtain recursive formula for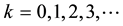
Thus, we obtain
The solution by DTM method:
By using Theorems of DTM, we have following recurrence relation:
Utilizing the recurrence relation, we find
Finally, the differential inverse transform of 
we obtain the following series solution
the closed form of above solution is
which is exactly the same as the exact solution.
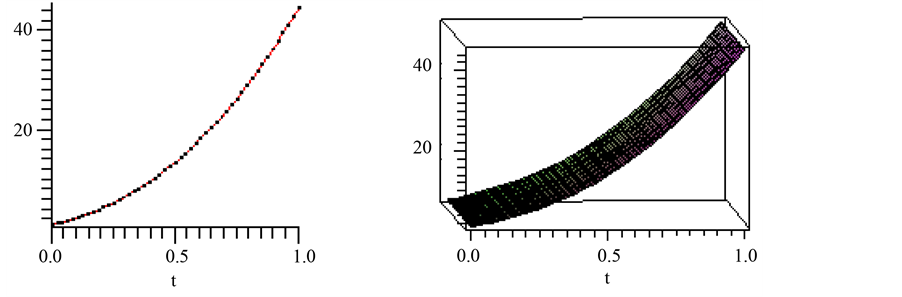
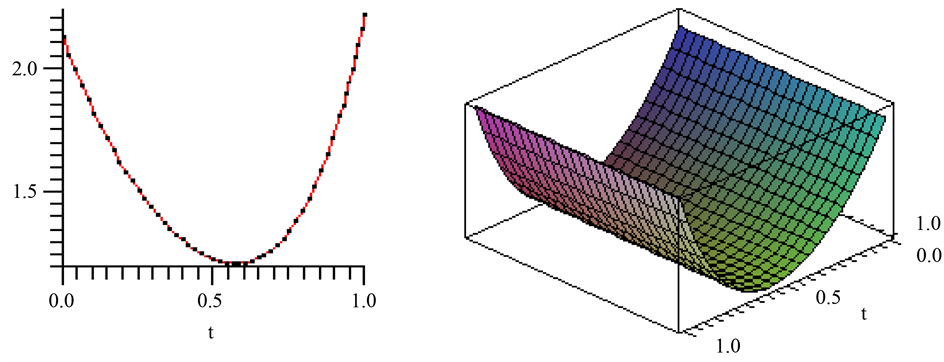
The obtained results (ADM and DTM) are exactly the same with the one found by exact solution. It is clear from Table 1 and Figure 1 that the three results not only give rapidly convergent series but also accurately compute the solutions.
Using our methods, we choose 6 points on [0, 1] respectively. The numerical results are given in the following Table 1.
Example 4.2 Solve the following nonlinear pantograph delay equation of first-order [3]
which has the exact solution,
The solution by ADM method:
By applying the ADM, according to Equations (3)-(10), we obtain
Figure 1. The obtained solution of the multi-pantograph delay equation [ADM solution (red), DTM solution (black), EXACT solution (blue)].
Table 1. Comparison of exact solution, the (ADM) and the (DTM) of y(t).
We have solved this problem using the proposed method. Recursive formula and the sequence of approximate solution are obtained as follows:
thus, we obtain:
Using to convergence of ADM’s method,
Here, the values of 
The solution by DTM method:
By using Theorems of DTM, we have following recurrence relation:
Utilizing the recurrence relation, we find
Finally, the differential inverse transform of 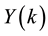
we obtain the following series solution
The obtained results (ADM and DTM) are exactly the same with each other. Increasing the approximation order up to the absolute differences between the numerical solutions are calculated for and comparisons have been made with known results as reported in Table 2 and Figure 2.
Example 4.3 Consider the following linear multi-pantograph delay equation of the first-order [21] .
The solution by ADM method:
By applying the ADM, according to Equations (3)-(10), we obtain
We have solved this problem using the proposed method. Recursive formula and the sequence of approximate solution are obtained as follows:
Figure 2. The obtained solution of the multi-pantograph delay equation [ADM solution (red), DTM solution (blue), EXACT solution (black)].
Table 2. Comparison of the ADM, the DTM and the EXACT solution.
Thus, we obtain:
The solution by DTM method:
By using Theorems of DTM, we have following recurrence relation:
Using the recurrence relation, we find
Finally, the differential inverse transform of 
we obtain the following series solution
The obtained results (ADM and DTM) are exactly the same with the one found by exact solution. It is clear from Table 3 and Figure 3 that the two results not only give rapidly convergent series but also accurately compute the solutions.
Example 4.4 Consider the following linear multi-pantograph delay equation of the first-order [21] .
The solution by ADM method:
By applying the ADM, according to Equations (3)-(10), we obtain
We have solved this problem using the proposed method. Recursive formula and the sequence of approximate solution are obtained as follows:
Figure 3. The obtained solution of the multi-pantograph delay equation [ADM solution (red), DTM solution (blue)].
Table 3. Comparison of the ADM solution 
Thus, we obtain:
Using to convergence of ADM’s method,
according to the obtained results ADM is convergent to the exact solution.
The solution by DTM method:
By using Theorems of DTM, we have following recurrence relation,
Utilizing the recurrence relation, we find
Finally, the differential inverse transform of 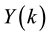
we obtain the following series solution
The obtained results (ADM and DTM) are exactly the same with the one found by exact solution. It is clear from Table 4 and Figure 4 that the two results not only give rapidly convergent series but also accurately compute the solutions.
5. Conclusion
It has been the aim of this paper to show that it appears natural to approximate the solution of multi-pantograph delay differential equation by ADM and DTM. We obtain the high approximate solutions or the exact solutions within a few iterations. It is concluded from figures and tables that the successive approximations methods are an accurate and efficient method to solve multi-pantograph delay differential equations. Some numerical examples have been provided to illustrate that the present method is effective in accuracy and convergence speed. In a word, the ADM and DTM show that the techniques are reliable, powerful and promising methods for linear
Figure 4. The obtained solution of the multi-pantograph delay equation [ADM solution (red), DTM solution (blue)].
Table 4. Comparison of the ADM solution 
and nonlinear problems.
Cite this paper
MusaCakir,DeryaArslan, (2015) The Adomian Decomposition Method and the Differential Transform Method for Numerical Solution of Multi-Pantograph Delay Differential Equations. Applied Mathematics,06,1332-1343. doi: 10.4236/am.2015.68126
References
- 1. Ockendon, J.R. and Taylor, A.B. (1971) The Dynamics of a Current Collection System for an Electric Locomotive. Proceedings of the Royal Society of London A, 322, 447-468.
http://dx.doi.org/10.1098/rspa.1971.0078 - 2. Li, D. and Liu, M. (2005) Runge-Kutta Methods for the Multi-pantograph Delay Equation. Applied Mathematics and Computation, 163, 383-395.
http://dx.doi.org/10.1016/j.amc.2004.02.013 - 3. Evans, D.J. and Raslan, K.R. (2005) The Adomian Decomposition Method for Solving Delay Differential Equation. International Journal of Computer Mathematics, 82, 49-54.
http://dx.doi.org/10.1080/00207160412331286815 - 4. Keskin, Y., at al. (2007) Approximate Solutions of Generalized Pantograph Equations by the Differential Transform Method. International Journal of Nonlinear Sciences and Numerical, 8, 159-164.
http://dx.doi.org/10.1515/IJNSNS.20078.2.159 - 5. Sezer, M. and Dascioglu, A.A. (2007) A Taylor Method for Numerical Solution of Generalized Pantograph Equations with Linear Functional Argument. Journal of Computational and Applied Mathematics, 200, 217-225.
http://dx.doi.org/10.1016/j.cam.2005.12.015 - 6. Yu, Z. (2008) Variational ?teration Method for Solving the Multi-Pantograph Delay Equation. Physics Letters A, 372, 6475-6479.
http://dx.doi.org/10.1016/j.physleta.2008.09.013� - 7. Sezer, M., Yalcinbas, S. and Sahin, N. (2008) Approximate Solution of Multi-Pantograph Equation with Variable Coefficients. Journal of Computational and Applied Mathematics, 214, 406-416.
http://dx.doi.org/10.1016/j.cam.2007.03.024 - 8. Geng, F.Z. and Qian, S.P. (2014) Solving Singularly Perturbed Multi-Pantograph Delay Equations Based on the Reprociding Kernel Medhod. Abstract and Applied Analysis, 2014, 6 p.
http://dx.doi.org/10.1155/2014/794716 - 9. Cherruault, Y., Adomian, G., Abbaoui, K. and Rach, R. (1995) Further Remarks on Convergence of Decomposition Method. International Journal of Bio-Medical Computing, 38, 89-93.
http://dx.doi.org/10.1016/0020-7101(94)01042-Y - 10. Ismail, H.N., Raslan, K.R. and Salem, G.S. (2004) Solitary Wave Solutions for the General KdV Equation by Adomian Decomposition Method. Applied Mathematics and Computation, 154, 17-29.
http://dx.doi.org/10.1016/S0096-3003(03)00686-6 - 11. El-Safty, A., Salim, M.S. and El-Khatib, M.A. (2003) Convergent of the Spline Functions for Delay Dynamic System. International Journal of Computer Mathematics, 80, 509-518.
http://dx.doi.org/10.1080/0020716021000014204 - 12. Rostam, K., Saeed, B. and Rahman, M. (2011) Differential Transform Method for Solving System of Delay Differential Equation. Australian Journal of Basic and Applied Sciences, 5, 201-206.
- 13. Adomian, G. (1994) Solving Frontier Problems of Physics: The Decomposition Method. Kluwer Academic Publishers, Boston.
http://dx.doi.org/10.1007/978-94-015-8289-6 - 14. Adomian, G. and Rach, R. (1993) Analytic Solution of Nonlinear Boundary-Value Problems in Several Dimensions by Decomposition. Journal of Mathematical Analysis and Applications, 174, 118-137.
http://dx.doi.org/10.1006/jmaa.1993.1105 - 15. Zhou, J.K. (1986) Differential Transform and Its Application for Electrical Circuits. Huazhong University Press, Wuhan.
- 16. Feng, X. (2013) An Analytic Study on the Multi-Pantograph Delay Equations with Variable Coefficients. Bulletin Mathematique de la society des Sciences mathématiques de Roumanie Tome, 56, 205-215.
http://ssmr.ro/bulletin/pdf/56-2/articol_7.pdf - 17. Ayaz, F. (2004) Applications of Differential Transform Method to Differential-Algebraic Equations. Applied Mathematics and Computation, 152, 649-657.
http://dx.doi.org/10.1016/S0096-3003(03)00581-2 - 18. Kurnaz, A. and Oturanc, G. (2005) The Differential Transform Approximation for the System Ordinary Differential Equations. International Journal of Computer Mathematics, 82, 709-719.
http://dx.doi.org/10.1080/00207160512331329050 - 19. Cherruault, Y. (1989) Convergence of Adomian’s Method. Kybernetes, 18, 31-38.
http://dx.doi.org/10.1108/eb005812 - 20. Hosseini, M.M. and Nasabzadeh, H. (2006) On the Convergence of Adomian Decomposition Method. Applied Mathematics and Computation, 182, 536-543.
http://dx.doi.org/10.1016/j.amc.2006.04.015 - 21. Liu, M.Z. and Li, D. (2004) Properties of Analytic Solution and Numerical Solution of Multi-Pantograph Equation. Applied Mathematics and Computation, 155, 853-871.
http://dx.doi.org/10.1016/j.amc.2003.07.017