Received 25 January 2015; accepted 13 February 2015; published 17 February 2015

ABSTRACT

We will study the generalized Steklov-Robin eigenproblem (with possibly matrix weights) in which the spectral parameter is both in the system and on the boundary. The weights may be singular on subsets of positive measure. We prove the existence of an increasing unbounded sequence of eigenvalues. The method of proof makes use of variational arguments.

Keywords:

Steklov-Robin, Variational Arguments, Matrix Weights

1. Introduction

We study the generalized Steklov-Robin eigenproblem. This spectrum includes the Steklov, Neumann and Robin spectra. We therefore generalize the results in [1] -[4] .

Consider the elliptic system

(1)

where, 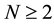is a bounded domain with boundary of class,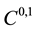

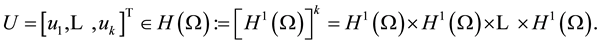Throughout this paper all matrices are symmetric. The matrix

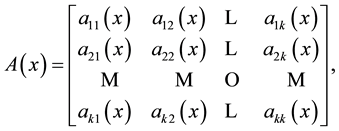
verifies the following conditions:

(A1) The functions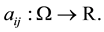

(A2) is positive semidefinite a.e. on Ω with 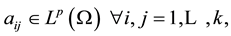for when, and when

The matrix

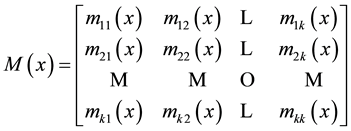
satisfies the following conditions:

(M1) 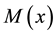is positive semidefinite a.e. on Ω The functions for when, and when

is the outward (unit) normal derivative on The matrix

verifies the following conditions:

(S1) The functions

(S2) is positive semidefinite a.e. on with for when, and when

and the matrix

(P1) is positive semidefinite a.e. on for when, and when

We assume that verify the following assumptions:

Assumption 1. 1) is positive definite on a set of positive measure of Ω,

2) is positive definite on a set of positive measure of

3) is positive definite on a set of positive measure of Ω with

4) is positive definite on a set of positive measure of

Remark 2. Assumption 1 is equivalent to

Remark 3. Since satisfy (A2), (S2), (M1), (P1) respectively, then we can write them in the following form (i.e.; eigen-decomposition of a positive semi-definite matrix or diagonalization)

where (i.e.; are orthogonal matrices) are the normalized eigenvectors, I is the identity matrix, is diagonal matrix and in the diagonal of are the eigenvalues of J (i.e.;) and

Remark 4. The weight matrices and may vanish on subsets of positive measure.

Definition 1. The generalized Steklov-Robin eigensystem is to find a pair with such that

(2)

Remark 5. Let in (2) if there is such an eigenpair, then and

Indeed, if or then

We have that which implies that and this implies that

a.e. (with) in Ω. This implies that is not positive definite on a subset of Ω of

positive measure, and then a.e. with on This implies

that is not positive definite on subset of of positive measure. So we have that, would be a constant vector function; which would contradict the assumptions (Assumption 1) imposed on and

Remark 6. If and then is an eigenvalue of the system (1) with eigenfunction vector function on.

It is therefore appropriate to consider the closed linear subspace (to be shown below) of under Assumption 1 defined by

Now all the eigenfunctions associated with (2) must belong to the -orthogonal complement

of this subspace in We will show that indeed is subspace of

Let and we wish to show that and

Therefore Now we show that

Since it follows that

By setting we get

Since for a.e. it readily follows that

that is, the vector satisfies

or equivalently

Hence,

since A similar arguments shows that

Therefore so we have that is a subspace of Thus, one can split the Hilbert space as a direct -orthogonal sum in the following way

Remark 7. 1) If in Ω, then the subspace provided on.

2) If in and, then the subspace provided on Ω.

・ We shall make use in what follows the real Lebesgue space for, and of the continuity and compactness of the trace operator

is well-defined, it is a Lebesgue integrable function with respect to Hausdorff dimensional measure. Sometimes we will just use U in place of when considering the trace of a function on. Throughout, this work we denote the -inner product by

and the associated norm by

(see [5] , [6] and the references therein for more details).

・ The trace mapping is compact (see [7] ).

(3)

defines an inner product for, with associated norm

(4)

Now, we state some auxiliary result, which will be need in the sequel for the proof of our main result. Using the Hölder inequality, the continuity of the trace operator, the Sobolev embedding theorem and lower semicontinuity of, we deduce that is equivalent to the standard -norm. This observation enables us to prove the existence of an unbounded and discrete spectrum for the Steklov-Robin eigenproblem (1) and discuss some of its properties.

Definition 2. Define the functional

and

Lemma 1. Suppose (A2), (S2), (M1), (P1) are met. Then the functionals and are C¹-functional (i.e.; continuously differentiable).

See [8] for the proof of Lemma 1.

Theorem 8. is G-differentiable and convex. Then is weakly lower-semi-continuous.

See [8] for the proof of Theorem 8.

2. Main Result

Theorem 9. Assume Assumption 1 as above, then we have the following.

1) The eigensystem (1) has a sequence of real eigenvalues

and each eigenvalue has a finite-dimensional eigenspace.

2) The eigenfunctions corresponding to the eigenvalues from an -orthogonal and - orthonormal family in (a closed subspace of).

3) The normalized eigenfunctions provide a complete -orthonormal basis of Moreover, each function has a unique representation of the from

(5)

In addition,

Proof of Theorem 9. We will prove the existence of a sequence of real eigenvalues and the eigenfunc-

tions corresponding to the eigenvalues that from an orthogonal family in.

We show that attains its minimum on the constraint set

Let by using the continuity of the trace operator, the Sobolev embedding theorem and

the lower-semi-continuity of

Let be a minimizing sequence in W₀ for since we have that by the definition of we have that for all and for all sufficiently large l, then by using the equivalent norm we have that, there is exist such that

so we have that

Therefore, this sequence is bounded in. Thus it has a weakly convergent subsequence

which convergent weakly to in. From Rellich-Kondrachov theorem this subsequence converges strongly to in so in W₀. Thus as the functional is weakly l.s.c. (see Theorem 8).

There exists such that. Hence, attains its minimum at and satisfies the following

(6)

for all We see that satisfies Equation (2) in a weak sense and this im-

plies that by the definition of W₀. Now take in Equation (6), we obtain that the eigenvalue is the infimum. This means that we could define by the Rayleigh quotient

Clearly,. Indeed assume that then on hence must be a constant and with that contradicts the assumptions imposed on. Thus.

Now we show the existence of higher eigenvalues.

Define

We know that the kernel of

Since W₁ is the null-space of the continuous functional on W₁ is a closed sub-

space of, and it is therefore a Hilbert space itself under the same inner product. Now

we define

Since then we have that. Now we define

we know that the kernel of

Since W₂ is the null-space of the continuous functional on, W₂ is a closed subspace of, and it is therefore a Hilbert space itself under the same inner product. Now

we define

Since then we have that Moreover, we can repeat the above arguments to show that

is achieved at some

We let

and

Since then we have that. Moreover, we can repeat the above arguments to show that

is achieved at some

Proceeding inductively, in general we can define

we know that the kernel of

Since W_j is the null-space of the continuous functional on, W_j is a closed subspace

of, and it is therefore a Hilbert space itself under the same inner product Now we define

In this way, we generate a sequence of eigenvalues

whose associated are c-orthogonal and -orthonormal in

Claim 1 as

Proof of claim 1. By way of contradiction, assume that the sequence is bounded above by a constant. Therefore, the corresponding sequence of eigenfunctions is bounded in By Rellich-Kondrachov theorem and the compactness of the trace operator, there is a Cauchy subsequence (which we again denote by), such that

(7)

Since the are -orthonormal, we have that, if

which contradicts Equation (7). Thus, We have that each occurs only finitely many times.

Claim 2

Each eigenvalue has a finite-dimensional eigenspace.

See [8] for the proof of claim 2.

We will now show that the normalized eigenfunctions provide a complete orthonormal basis of. Let

so that

Claim 3

The sequence is a maximal -orthonormal family of. (We know that the set is

maximal -orthonormal if and only if it is a complete orthonormal basis).

Proof of Claim 3. By way of contradiction, assume that the sequence is not maximal, then there exists a and such that and, i.e.;

since. Therefore. We have that. It follows from the definition of that

Since we know from Claim 1 that as we have that Therefore a.e in Ω, which contradicts the definition of ξ. Thus the sequence is a maximal -orthonormal family of so the sequence provides a complete orthonormal basis of that is, for any, with and

Now let

Therefore,

and

Claim 4

We shall show that

Proof of Claim 4.

Thus

References