Applied Mathematics
Vol.05 No.19(2014), Article ID:51279,9 pages
10.4236/am.2014.519295
Effluent Discharges from Two Outfalls on a Sloping Beach
Anton Purnama
Department of Mathematics and Statistics, College of Science, Sultan Qaboos University, Muscat, Sultanate of Oman
Email: antonp@squ.edu.om
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 August 2014; revised 10 September 2014; accepted 7 October 2014
ABSTRACT
A marine outfall is a long pipeline that continuously discharges large amounts of effluent streams into the sea. As the number of marine outfalls along the coastal areas is growing, a far field mathematical model with two point sources on a sloping beach is used to assess the coastal water quality following discharges from two outfalls. Asymptotic approximation will be made to the concentration at the beach to measure how well the effluent plumes are mixed and diluted in the coastal waters. The result found agrees with the engineering practice of installing a two-port diffuser at the end of a single outfall to minimize its potential environment impacts.
Keywords:
Advection Diffusion Equation, Far Field Model, Two-Port Diffuser, Two Point Sources

1. Introduction
Most coastal industrial installations and plants, such as municipal sewage treatment plants [1] [2] , power generation stations [3] , and seawater desalination plants [4] - [8] , dispose of their wastewater effluents through long outfall pipes that stretch far into the ocean. For a modern plant, a multiport diffuser would also be installed at the pipe-end to rapidly dilute the effluent stream. Because of relatively shallow coastal waters, it is observed that the elongated effluent plumes are spreading towards the shoreline and may cause a concentration build-up [9] - [11] . Due to the uncertainty in sea conditions, a clear understanding of the mixing processes of effluent plumes is not yet known, and the use of mathematical models has been a key strategy for the basis of sound engineering design and for assessing the potential environmental impacts of marine outfall effluent discharges [2] [3] [5] - [8] .
When many marine outfalls are discharging effluents to shallow coastal waters, the adverse long-term impacts are strongly inter-dependent, and compounded from neighbouring outfalls. The interactions of two or more effluent plumes are expected as many outfalls often tend to be closely clustered together along the coastal areas. Newly-constructed coastal plants may need to build two outfalls as a contingency plan for a future increase in the plant’s production capacity [6] . For two outfalls discharging a given integrated total effluent stream, the waste load can be allocated optimally between them to minimise the impact [12] [13] .
As coastal industrial plants are built predominantly on the sloping sandy beaches, a mathematical model using a two-dimensional advection diffusion equation with two point sources is presented. The solution is plotted to graphically study the merging of two effluent plumes from two outfalls. While the far field modelling in this paper involves drastic simplifications, key physical mixing and dispersion processes are represented, and thus the analytical solution remains useful in providing a qualitative understanding and in suggesting general behaviour of the marine outfall effluent discharge plumes in coastal environment [9] [11] [12] .
2. Mathematical Analysis
The beach is considered to be straight and the sea wide, and the outfall’s effluent plume is assumed to be vertically well-mixed over the water depth. The coastal (drift) current is assumed to be steady with a speed
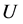 and remains in the
and remains in the
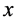 -direction parallel to the beach at all times. The dispersion mechanisms are represented by eddy diffusivities, and diffusion in the
-direction parallel to the beach at all times. The dispersion mechanisms are represented by eddy diffusivities, and diffusion in the
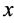 -direction is neglected, as the effluent plumes in steady currents become very elongated in the
-direction is neglected, as the effluent plumes in steady currents become very elongated in the
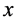 -direction. The variations in the
-direction. The variations in the
 -direction of
-direction of
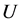 and coefficient of dispersivity
and coefficient of dispersivity
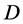 are assumed as the power functions only of water depth
are assumed as the power functions only of water depth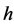 , and for application, we take
, and for application, we take
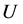 to be proportional to
to be proportional to
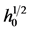 and
and
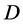 to
to , where
, where
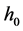 is an arbitrary reference water depth. These scalings are appropriate for a turbulent shallow water flow over a smooth bed [9] - [11] [14] . For simplicity, other complexities such as tidal motions, density and temperature are ignored.
is an arbitrary reference water depth. These scalings are appropriate for a turbulent shallow water flow over a smooth bed [9] - [11] [14] . For simplicity, other complexities such as tidal motions, density and temperature are ignored.
As illustrated in Figure 1, we represent the old outfall as a point source at the position
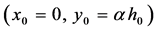 discharging an effluent stream at a constant rate
discharging an effluent stream at a constant rate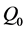 , where
, where
 is the source length. Similarly, the new outfall as a point source at
is the source length. Similarly, the new outfall as a point source at





As the water depth is gradually decreasing towards the beach at




with boundary condition










where

Figure 1. Diagram of two sea outfalls.



the analytical solution of Equation (1) is given by

where











As a higher build-up in concentration is more likely found at the shallow water close to the beach [7] [8] [10] [14] , the appropriate measure for assessing the impact of marine effluent discharges from sea outfalls would be the concentration values at the beach. In the limit as



It is easy to see for effluent discharges from a single point source at




The concentration at the beach for a point source length







3. Two Independent Outfalls
Apart from the effluent discharge rates, the compounded impact of the new outfall is governed by the outfall’s separation distances






We first consider the case where the two outfalls are operated independently by two coastal plants, i.e., when











Since the value







Next, the compounded concentration at the beach for two point sources as given by Equation (3) can be simplified to
Figure 2. The concentration at the beach for a single point source.

Figure 4 shows the concentration at the beach for the two cases illustrated in Figure 3, where two separated plumes are depicted as two distinctive peaks. For comparison, the concentration for the single point source with


Substituting


where


By differentiating,




Note that for a given value of


As shown in Figure 5, the largest maximum value of compounded concentration at the beach for two point sources is always greater than that of the concentration at the beach for a single point source. The contribution of the new outfall is much greater for



value of the concentration at the beach is
Figure 3. Merging contour of two point sources plumes when


equal rates, i.e.





Figure 4. Compounded concentration at the beach for two point sources.
Figure 5. Maximum value of
4. Single Outfall with Two Ports
Modifying the rates of discharge can be achieved through a relatively less expensive method than extending the outfall lengths. For the case where two outfalls is operated by one plant, i.e. when


That is, the maximum value of


To include the case of the modern engineering practice that installs two ports at the end of a marine outfall [5] [6] , we also assume that both port separation distances





For plotting the contours of the effluent plume, since the point sources are close to each other, and in the limit as



The contours of the solution for a single outfall with two ports are reproduced graphically in Figure 6 for






Finally, the maximum value of compounded concentration at the beach for two closely located point sources can be approximated to

Again, the maximum value of









5. Conclusions
The solutions for an advection diffusion equation with two point sources are applied to study the interaction and merging of effluent discharge plumes from two outfalls on a sloping beach. As a measure for assessing the impact in the coastal environment, the maximum compounded concentration at the beach is formulated. If the two outfalls are independently operated, then the maximum value of the concentration at the beach can be minimized as long as the new outfall length is more than double the old outfall length, and discharging at a rate smaller than the old outfall.
If two outfalls are operated by one plant, then the integrated total effluent load can be shared between them, and it is found that the maximum value of the concentration at the beach is smaller than that of the single outfall. A similar result is also obtained for a single outfall where a two-port diffuser is installed at the end outfall pipe. However, implementation issues related to the control of discharge rates, reliability and cost effectiveness of the marine outfall are not addressed.
The mathematical formulation presented can be extended to the case of multiple outfalls discharging on a coastal area, and in particular, the result for effluent discharges from multiport diffusers has been reported in [11] .
Figure 6. Combined plumes of two closely located point sources for


Figure 7. Maximum value of
Acknowledgements
The author is grateful to Sultan Qaboos University for an Internal Grant IG/SCI/DOMS/14/01 which provided financial support for this work.
References
- Institution of Civil Engineers (2001) Long Sea Outfalls. Thomas Telford Ltd., London.
- Signell, R.P.,Jenter, H.L. and Blumberg A.F. (2000)Predicting the Physical Effects of Relocating Boston’s Sewage Outfall. Estuarine, Coastal and Shelf Sciences, 50, 59-71. http://dx.doi.org/10.1006/ecss.1999.0532
- Macqueen, J.F. and Preston, R.W. (1983) Cooling Water Discharges into a Sea with a Sloping Bed. Water Research, 17, 389-395. http://dx.doi.org/10.1016/0043-1354(83)90134-3
- Lattemann, S. and Hopner, T. (2008) Environmental Impact and Impact Assessment of Seawater Desalination. Desalination, 220, 1-15. http://dx.doi.org/10.1016/j.desal.2007.03.009
- Bleninger, T. and Jirka, G.H. (2008) Modelling and Environmentally Sound Management of Brine Discharges from Desalination Plants. Desalination, 221, 585-597. http://dx.doi.org/10.1016/j.desal.2007.02.059
- Purnama, A., Al-Barwani, H.H., Bleninger, T. and Doneker, R.L. (2011) CORMIX Simulations of Brine Discharges from Barka Plants, Oman. Desalination and Water Treatment, 32, 329-338. http://dx.doi.org/10.5004/dwt.2011.2718
- Roberts, D.A., Johnston, E.L. and Knott, N.A. (2010) Impacts of Desalination Plant Discharges on the Marine Environment: A Critical Review of Published Studies. Water Research, 44, 5117-5128. http://dx.doi.org/10.1016/j.watres.2010.04.036
- Palomar, P. and Losada, I.J. (2011) Impacts of Brine Discharge on the Marine Environment. Modelling as a Predictive Tool. In: Schorr, M., Ed., Desalination, Trends and Technologies, InTech Open Access Publisher, Rijeka, Croatia, 279-310.
- Al-Barwani, H.H. and Purnama, A. (2009) Analytical Solutions for Brine Discharge Plumes on a Sloping Beach. Desalination and Water Treatment, 11, 2-6. http://dx.doi.org/10.5004/dwt.2009.835
- Kay, A. (1987) The Effect of Cross-Stream Depth Variations upon Contaminant Dispersion in a Vertically Well-Mixed Current. Estuarine and Coastal Shelf Science, 24, 177-204. http://dx.doi.org/10.1016/0272-7714(87)90064-3
- Purnama, A. (2012) Merging Effluent Discharge Plumes from Multiport Diffusers on a Sloping Beach. Applied Mathematics, 3, 24-29. http://dx.doi.org/10.4236/am.2012.31004
- Smith, R. and Purnama, A. (1999) Two Outfalls in an Estuary: Optimal Wasteload Allocation. Journal of Engineering Mathematics, 35, 273-283. http://dx.doi.org/10.1023/A:1004332007489
- Bikangaga, J.H. and Nassehi, V. (1995) Application of Computer Modeling Techniques to the Determination of Optimum Effluent Discharge Policies in Tidal Water Systems. Water Research, 29, 2367-2375. http://dx.doi.org/10.1016/0043-1354(95)00045-M
- Smith, R. (1976) Longitudinal Dispersion of Buoyant Contaminant in a Shallow Channel. Journal of Fluid Mechanics, 78, 677-688. http://dx.doi.org/10.1017/S0022112076002681
- Murphy, G.M. (1960) Ordinary Differential Equations and Their Solutions. D. Van Nostrand, London.
- Gradshteyn, I.S. and Ryzhik, I. (1980) Tables of Integrals, Series and Products. Academic Press, London.








