Applied Mathematics
Vol.05 No.21(2014), Article ID:52265,9 pages
10.4236/am.2014.521325
New Oscillation Criteria of Second-Order Nonlinear Delay Dynamic Equations on Time Scales
Quanxin Zhang, Li Gao
Department of Mathematics, Binzhou University, Shandong, China
Email: 3314744@163.com, gaolibzxy@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 September 2014; revised 22 October 2014; accepted 10 November 2014
ABSTRACT
By using the generalized Riccati transformation and the integral averaging technique, the paper establishes some new oscillation criteria for the second-order nonlinear delay dynamic equations on time scales. The results in this paper unify the oscillation of the second-order nonlinear delay differential equation and the second-order nonlinear delay difference equation on time scales. The Theorems in this paper are new even in the continuous and the discrete cases.
Keywords:
Oscillation Criterion, Dynamic Equations, Time Scale

1. Introduction
According to the important academic value and application background in Quantum Physics (especially in Nuclear Physics), engineering mechanics and control theory, the oscillation theory of dynamic equations on time scales has become one of the research hotspots. The paper will deal with the oscillatory behavior of all solutions of second-order nonlinear delay dynamic equation
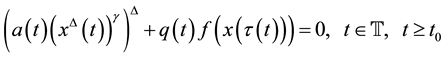 (1)
(1)
In order to obtain the main results, we give the following hypotheses:
(H1) 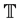 is a time scale (i.e., a nonempty closed subset of the real numbers
is a time scale (i.e., a nonempty closed subset of the real numbers ) which is unbounded above, and
) which is unbounded above, and  with
with . We define the time scale interval of the form
. We define the time scale interval of the form 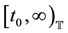 by
by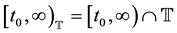 .
.
(H2)  is the ratio of two positive odd integers.
is the ratio of two positive odd integers.
(H3) a, q are positive real-valued right-dense continuous functions on an arbitrary time scale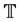 .
.
(H4) 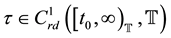 is a strictly increasing function such that
is a strictly increasing function such that  and
and 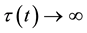 as
as 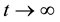 and
and .
.
(H5) 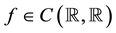 is a continuous function, for some positive constant L which satisfies
is a continuous function, for some positive constant L which satisfies
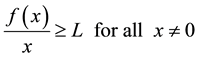
According to the solution of (1), we mean a nontrivial real-valued function x satisfying (1) for



and

It is easy to see that (1) can be transformed into a second-order nonlinear delay dynamic equation

where



In (4), if

In (6), if

After the careful consideration of the linear delay dynamic equations by Agarwal, Bohner and Saker in 2005 [1] (7) and the nonlinear delay dynamic equations by Sahiner [2] (6), some sufficient conditions for oscillation of (7) and (6) have been established. In 2007, Erbe, Peterson and Saker [3] considered the general nonlinear delay dynamic equations (4) and obtained some new oscillation criteria, which improved the results given by Sahiner [2] . Saker [4] in 2005 and Grace, Bohner and Agarwal [5] in 2009 considered the half-linear dynamic equations (5), and established some sufficient conditions for oscillation of (5). For other related results, we recommend the references [6] -[10] . On the basis of these, by using the generalized Riccati transformation and integral averaging technique, we continue to discuss the oscillation of solutions of (1) and obtain some new oscillatory criteria of Philos-type for (1).
A time scale 


A point 







Throughout this paper, we will make use of the following product and quotient rules for the derivative of the product fg and the quotient 


For 

The integration by parts formula reads

and infinite integrals are defined by
For more details, see [11] [12] .
2. Main Results
In order to obtain the main results, the following lemmas are first introduced.
Lemma 1 (Han et al. [[10] , Lemma 2.2]) Assume that 








Lemma 2 (Bohner et al. [[11] , Theorem 1.90]) Assume that 

Lemma 3 (Sun et al. [[13] , Lemma 2.1]) Assume that the conditions (H1)-(H5) and (2) hold, and let 


Next, we will provide a new sufficient condition for oscillation of all solutions of (1), which can be considered as the extension of the result of Philos [14] for oscillation of second-order differential equations.
Theorem 1 Assume that the conditions (H1) - (H5), (2) hold and

and H has a non-positive continuous Δ-partial derivative 

Assume that there exists a positive nondecreasing Δ-differentiable function 

for


Proof. Suppose that 








Then on


by using (11), we have 

By 


Substituting (17) in (16), we obtain








Substituting (19) into (18), we obtain

where



By (21), we obtain
From the above inequality, denoting
The above inequality implies that
So we have a contradiction to the condition (14). This completes the proof.
Remark 1 From Theorem 1, we can obtain different conditions for oscillation of all solutions of (1) with different choices of 



Now, let us consider the function 
Then 





the function h with 


Corollary 1 Assume that the conditions (H1) - (H5), (2) hold and



for


Now, when (3) holds, we give the oscillatory criteria of Philos-type for (1).
Theorem 2 Assume that the conditions (H1) - (H5), (3) hold and



where
Then (1) is oscillatory on
Proof. Suppose that 








(1) 

(2) 

Case (1). The proof when 
Case (2). For
and hence

Integrating (24) from 


and thus

where

Integrating (26) from t1 to t, we have
so that

Integrating (27) from t1 to t, we obtain
by (23), which is a contradiction. This completes the proof.
Remark 2 In the past, the usual result is that the condition (3) was established, then every solution of the Equation (1) is either oscillatory or converges to zero. But now Theorem 2 in our paper prove that if the condition (3) is satisfied, every solution of the Equation (1) is oscillatory.
Similar to the Corollary 1, by applying Theorem 2 with
we have the following results.
Corollary 2 Assume that the conditions (H1) - (H5), (3), (22), (23) hold and

Next, we give a result of a succinctness and convenient to application.
Theorem 3 Assume that the conditions (H1) - (H5), (2) hold and

and H has a non-positive continuous Δ-partial derivative 


for


Proof. Suppose that 







for all
for all

and hence, for all
Thus
which is contradicted with (28). This completes the proof.
Now, applying Theorem 3 with
we have the following results.
Corollary 3 Assume that the conditions (H1) - (H5), (2) hold and



for


Using the same ideas as in the proof of Theorem 2, when (3) holds, we can now obtain the following result.
Theorem 4 Assume that the conditions (H1) - (H5), (3), (23) hold and

Now, let
we have the following results.
Corollary 4 Assume that the conditions (H1) - (H5), (3), (23), (30) hold and

Remark 3 Our results in this paper unify the oscillation of the second-order nonlinear delay differential equation and the second-order nonlinear delay difference equation. As an example, when
and the condition (30) becomes
then Corollary 3 extends Theorem 2.1 in [15] and Theorem 1 generalizes Theorem 2.1 in [15] . The Theorem 2 - 4 in this paper are new even for the cases 

Example 1 Consider the second-order nonlinear delay 2-difference equations

Here
The conditions (H1) - (H4) and (2) are clearly satisfied, (H5) holds with L = 1. Now let 

so that (30) is satisfied as well. Altogether, by Corollary 3, the equation (31) is oscillatory.
Acknowledgements
We thank the Editor and the referee for their comments. This research is supported by the Natural Science Foundation of Shandong Province of China under Grant No. ZR2013AM003.
References
- Agarwal, R.P., Bohner, M. and Saker, S.H. (2005) Oscillation of Second Order Delay Dynamic Equations. Quarterly of Applied Mathematics, 13, 1-18.
- Sahiner. Y. (2005) Oscillation of Second Order Delay Differential Equations on Time Scales. Nonlinear Analysis: Theory, Methods & Applications, 63, 1073-1080. http://dx.doi.org/10.1016/j.na.2005.01.062
- Erbe, L., Peterson, A. and Saker, S.H. (2007) Oscillation Criteria for Second Order Nonlinear Delay Dynamic Equations. Journal of Mathematical Analysis and Applications, 333, 505-522. http://dx.doi.org/10.1016/j.jmaa.2006.10.055
- Saker, S.H. (2005) Oscillation Criteria of Second-Order Half-Linear Dynamic Equations on Time Scales. Journal of Computational and Applied Mathematics, 177, 375-387. http://dx.doi.org/10.1016/j.cam.2004.09.028
- Grace, S.R., Bohner, M. and Agarwal, R.P. (2009) On the Oscillation of Second-Order Half-Linear Dynamic Equations. Journal of Difference Equations and Applications, 15, 451-460. http://dx.doi.org/10.1080/10236190802125371
- Bohner, M. and Saker, S.H. (2004) Oscillation of Second Order Nonlinear Dynamic Equations on Time Scales. Rocky Mountain Journal of Mathematics, 34, 1239-1245. http://dx.doi.org/10.1216/rmjm/1181069797
- Erbe, L. (2001) Oscillation Criteria for Second Order Linear Equations on a Time Scale. The Canadian Applied Mathematics Quarterly, 9, 345-375.
- Zhang, Q., Song, X. and Gao, L. (2012) On the Oscillation of Second-Order Nonlinear Delay Dynamic Equations on Time Scales. Applied Mathematics & Information Sciences, 30, 219-234.
- Zhang, Q., Gao, L. and Wang, L. (2011) Oscillation of Second-Order Nonlinear Delay Dynamic Equations on Time Scales. Computers & Mathematics with Applications, 61, 2342-2348. http://dx.doi.org/10.1016/j.camwa.2010.10.005
- Han, Z., Li, T., Sun, S. and Zhang, C. (2009) Oscillation for Second-Order Nonlinear Delay Dynamic Equations on Time Scales. Advances in Difference Equations, Article ID: 756171, 13 pages.
- Bohner, M. and Peterson, A. (2001) Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston. http://dx.doi.org/10.1007/978-1-4612-0201-1
- Bohner, M. and Peterson, A. (2003) Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston. http://dx.doi.org/10.1007/978-0-8176-8230-9
- Sun, S., Han, Z. and Zhang, C. (2009) Oscillation of Second Order Delay Dynamic Equations on Time Scales. Journal of Applied Mathematics and Computing, 30, 459-468. http://dx.doi.org/10.1007/s12190-008-0185-6
- Philos, Ch.G. (1989) Oscillation Theorems for Linear Differential Equations of Second Order. Archiv der Mathematik, 53, 482-492. http://dx.doi.org/10.1007/BF01324723
- Saker, S.H. (2003) Oscillation Theorems for Second-Order Nonlinear Delay Difference Equations. Periodica Mathematica Hungarica, 47, 201-213. http://dx.doi.org/10.1023/B:MAHU.0000010821.30713.be
































