Received 18 July 2014; revised 16 August 2014; accepted 2 September 2014

ABSTRACT

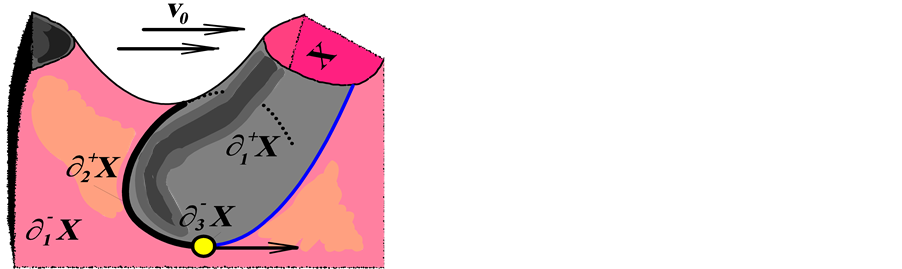
As has been observed by Morse [1] , any generic vector field v on a compact smooth manifold X with boundary gives rise to a stratification of the boundary by compact submanifolds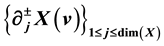, where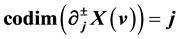. Our main observation is that this stratification reflects the stratified convexity/concavity of the boundary with respect to the -flow. We study the behavior of this stratification under deformations of the vector field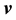. We also investigate the restrictions that the existence of a convex/concave traversing 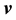-flow imposes on the topology of X. Let 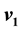be the orthogonal projection of 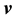on the tangent bundle of. We link the dynamics of the -flow on the boundary with the property of in X being convex/concave. This linkage is an instance of more general phenomenon that we call “holography of traversing fields”―a subject of a different paper to follow.

Keywords:

Morse Theory, Gradient Flows, Convexity, Concavity, Manifolds with Boundary

1. Introduction

This paper is the first in a series that investigates the Morse Theory and gradient flows on smooth compact manifolds with boundary, a special case of the well-developed Morse theory on stratified spaces (see [2] -[4] ). For us, however, the starting point and the source of inspiration is the 1929 paper of Morse [1] .

We intend to present to the reader a version of the Morse Theory in which the critical points remain behind the scene, while shaping the geometry of the boundary! Some of the concepts that animate our approach can be found in [5] , where they are adopted to the special environment a 3 D-gradient flows. These notions include stratified convexity or concavity of traversing flows in connection to the boundary of the manifold. That concavity serves as a measure of intrinsic complexity of a given manifold 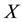with respect to any traversing flow. Both convexity and concavity have strong topological implications.

Another central theme that will make its first brief appearance in this paper is the holographic properties of traversing flows on manifolds with boundary. The ultimate aim here is to reconstruct (perhaps, only partially) the bulk of the manifold and the dynamics of the flow on it from some residual structures on the boundary, thus the name “holography”.

In Section 2, for so-called boundary generic fields 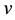on 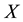(see Definition 2.1), we explore the Morse stratification of the boundary (see Formula (1) and [1] ), induced by the vector field on.

In Section 3, we investigate the degrees of freedom to change this stratification by deforming a given vector field within the space of gradient-like fields (Theorem 3.2, Corollary 3.2, and Corollary 3.3).

In Section 4, for vector fields on compact manifolds, we introduce the pivotal notion of boundary -convexity/-concavity, (see Definition 4.1). Then we explore some topological implications of the existence of a boundary -convex/-concave traversing field on (see Lemma 4.2, Corollary 4.2, Corollary 4.3, and Corollary 4.4).

Let denote the orthogonal projection of the field on the bundle tangent to the boundary. Occasionally, we can determine whether a given field is convex/concave just by observing the behavior of the -trajectories on the boundary (Theorem 4.1, Theorem 4.2). We view the possibility of such determination as an instance of a more general phenomenon, which we call “holography”. This phenomenon will occupy us fully in a different paper.

The Eliashberg surgery theory of folding maps [6] [7] helps us to describe the patterns of Morse stratifications for traversing 3-concave and 3-convex fields (Theorem 5.1, Conjecture 5.1, and Corollary 5.1).

2. The Morse Stratification

Inspired by [1] , we start by introducing some basic notions and constructions that describe the way in which generic vector fields on a compact smooth manifold interact with its boundary.

Let be a compact smooth -dimensional manifold with a boundary. Let v be a smooth vec- tor field on which does not vanish on the boundary. As a rule, we assume that X is properly contained in a -dimensional manifold and that the field v extends to a field on so that. In fact, we always treat the pair as a germ of a space and a field in the vicinity of the given pair.

Often we will consider vector fields only with the isolated Morse-type singularities (zeros) located away from the boundary. This means that v, viewed as a section of the tangent bundle, is transversal its zero section. In other words, in the vicinity of each singular point, there is a local system of coordinates such that the field v can be represented as, where all.

To achieve some uniformity in our notations, let and.

The vector field v gives rise to a partition of the boundary into two sets: the locus, where the field is directed inward of, and, where it is directed outwards. We assume that, viewed as a section of the quotient line bundle over, is transversal to its zero section. This assumption implies that both sets are compact manifolds which share a common boundary . Evidently, is the locus where is tangent to the boundary.

Morse has noticed that, for a generic vector field ν, the tangent locus inherits a similar structure in con- nection to, as has in connection to (see [1] ). That is, gives rise to a partition of into two sets: the locus, where the field is directed inward of, and, where it is directed outward of. Again, let us assume that v, viewed as a section of the quotient line bundle over, is transversal to its zero section.

For generic fields, this structure replicates itself: the cuspidal locus is defined as the locus where v is tangent to; is divided into two manifolds, and. In, the field is directed inward of, in, outward of. We can repeat this construction until we reach the zero-dimensional stratum (see Figure 1 and Figure 2 which depict these strata for fields in).

These considerations motivate

Definition 2.1 We say that a smooth field v on is boundary generic if:

・ ,

・ , viewed as a section of the tangent bundle, is transversal to its zero section,

・ for each, the -generated stratum is a smooth submanifold of,

・ the field, viewed as section of the quotient 1-bundle

,

is transversal to the zero section of for all.

We denote the space of smooth boundarygeneric vector fields on by the symbol.

Thus a boundary generic vector field on gives rise to two stratifications:

(1)

, the first one by closed submanifolds, the second one―by compact ones. Here .

For simplicity, the notations “” do not reflect the dependence of these strata on the vector field. When the field varies, we use a more accurate notation “”.

Remark 2.1. Replacing with affects the Morse stratification according to the formula:

where when, and otherwise.

We will postpone the proof of the theorem below until the second paper in this series of articles (see [8] , Theorem 3.4, an extension of Theorem 2.1 below). There we will develop the needed analytical tools.

Theorem 2.1 Boundary generic vector fields form an open and dense subset in the space of all smooth fields on.

Definition 2.2 We say that a smooth vector field on is of the gradient type (or gradient-like) for a smooth function if:

・ the differential and the field vanish on the same locus,

・ the function in,

・ in the vicinity of, there exist a Rimannian metric on so that, the gradient field of in the metric.

Definition 2.3 A smooth function is called Morse function if its differential, viewed as a section of the cotangent bundle, is transversal to the zero section.

Recall that, for a Morse function on a compact -manifold X, the critical set

is finite, and each point has special local coordinates such that, where

for all (for example, see [9] ).

Definition 2.4 Let be a smooth function and its gradient-like vector field. We say that the pair is boundary generic if the field is boundary generic in the sense of Definition 2.1 and the res- trictions of to each stratum are Morse functions for all.

Lemma 2.1 Let be a compact smooth manifold, and a smooth manifold which is stratified by sub- manifolds. Let be the space of smooth maps which are transversal to each stratum. Put. Next consider the space of pairs such that

and has the property: are Morse functions for all. Then is open and dense in the

space.

Proof. Consider the space, where denotes the cotangent bundle of. The property is equivalent to the property of the section of the bundle

to be transversal to each (transversal) intersection of the -graph with each stratum. The latter property defines a open set in.

In order to validate density of in, we first perturb a given map to make it transversal to each stratum, and then perturb a given function to make the section of transversal to each manifold.

Theorem 2.2 The boundary generic1 Morse pairs on a compact manifold form an open and dense subset in the space of all smooth functions and their gradient-like fields.

Proof. By Theorem 2.1, the boundary generic fields form an open and dense set in the space of all fields.

Let be a complete flag in, formed by subspaces of codimension j. In the proof of Theorem 3.4 [8] , for every field, we will construct a smooth map such that. Moreover, is transversal to each, if and only if, is a boundary generic field. The construction of the map utilizes high order Lie derivatives of an auxiliary function as in Lemma 3.1 [8] .

Now the property of boundary generic Morse pairs to be open and dense in the space of all pairs follows from Lemma 2.1: just let, , , and in that lemma.

For the reader convenience, let us sketch now an alternative argument that establishes just the density of boundary generic Morse pairs in the space of all pairs. It does not rely on the construction of the map from [8] .

We start with a pair where and at the points of the set where. By a small perturbation of, we can assume the is a Morse function on and its gradient-like field.

Let be a compact regular neighborhood of in so small that. By Theorem 2.1, we can perturb to a new field so that is boundary generic in the sense of Definition 2.1 and still.

For a given, the condition defines an open cone in the space of all fields, subject to the constraint. Therefore can be chosen both boundary generic and gradient-like for. When is fixed, so are the stratifications.

Next, with being fixed, we perturb again to a new function so that and

are Morse functions for all j. The perturbation will be supported in the compact. We start

constructing inductively first from adjusting it on the 1-manifold and then moving sequentially to the strata with lower indices j. We pick each perturbation so small that the open condition is not violated. The existence of the desired -th perturbation is based on the fact that Morse functions on a compact manifold (in this case, on) form an open and dense subset in, the space of all smooth functions on, being equipped with the Whitney topology. Note that since is tangent

to along and, the restriction has no critical points in the vi-

cinity of. Thus we need to perturb only on a compact subset which has an

empty intersection with. This perturbation extends smoothly from to. Eventually, we reach the upper stratum, thus constructing a boundary generic approximation of the given pair.

All the changes of, but the first one, we have introduced so far are supported in, where

and. This proves that the boundary generic pairs form a dense set in the space of all pairs, where being a -gradient-like field, subject to the constraints:, and being a Morse function.

For a given Morse pair, we denote by the set of critical points of the function. For a boundary generic Morse pair, the finite critical set is divided into two complementary sets: the set of positive critical points and the set of negative ones (see Figure 3).

Remark 2.2. Note that when, it may happen that. However, if a component of is a closed manifold, then must have local extrema, in which case.

Consider a generic field and a Riemannian metric on. We denote by the orthogonal projection of the field on the tangent space. Note that if is a gradient field for a function in metric, then is automatically a gradient field for the restrictions and.

Take a smooth vector field on a compact -manifold with isolated singularities

. We denote by the localized index of at its typical singular point. In a

local chart, is defined as the degree of a map from a small -centered -sphere

to the unit -sphere. The map takes each point to the point.

We define the “global” index as the sum.

For a generic field and a Riemannian metric on, we form the fields on and define the global index of by the formula:

Let us revisit the beautiful Morse formulas [1] :

Theorem 2.3 (The Morse Law of Vector Fields) For a boundary generic vector field and a Riemannian metric on a -manifold, such that the singularities of the fields are isolated for all, the following two equivalent sets of formulas hold:

(2)

where stands for the Euler number of the appropriate space2.

For vector fields with symmetry, the Morse Law of Vector Fields has an equivariant generalization [10] . Here is its brief description: for a compact Lie group acting on a compact manifold, equipped with a

-equivariant field, we prove that the invariants can be interpreted as taking values in the

Burnside ring of the group (see [11] for the definitions). With this interpretation in place, the appearance of Formula (2) does not change.

Morse Formula (2) has an instant, but significant implication:

Corollary 2.1 Let be a smooth neighborhood of the zero set of a vector field on a compact -manifold. Assume that is boundary generic with respect to both boundaries, and. Then

Remark 2.3. Therefore, the numbers

can serve as “more and less localized” definitions of the index invariant.

An interesting discussion, connected to Theorem 2.3, its topological and geometrical implications, can be found in the paper of Gotlieb [12] . The “Topological Gauss-Bonnet Theorem” below is a sample of these re- sults.

Theorem 2.4 (Gotlieb) Let be a compact smooth -dimensional manifold and a smooth map which is a immersion in the vicinity of the boundary. Let be a Riemannian metric on which, in the vicinity of, is the pull-back of the Euclidean metric on. Consider a generic linear function such that the composite function has only isolated singularities in the interior of. Let be the gradient field of 3. Assume that is boundary generic.

Then the degree of the Gauss map

can be calculated either by integrating over the normal curvature (in the metric) of the hyper- surface, or in terms of the -induced stratification

by the formula

(3)4

Example 2.1. Let X be an orientable surface of genus g with a single boundary component. Let be an immersion, and let, and be as in Theorem 2.4.

Since Ф is an immersion everywhere (and not only in the vicinity of ∂X as Theorem 2.4 presumes), we get that. Thus. Then Theorem 2.4 claims that the degree of the Gauss map is equal to

Thus, the topological Gauss-Bonnet theorem, for immersions, reduces to the equation

.

So the number of -trajectories in that are tangent to, but are not singletons (they correspond to points of), as a function of genus, grows at least as fast as.

On the other hand, by the Whitney index formula [13] , the degree of can be also calculated as, where denotes the number of positive/negative self-intersections of the curve, and.

By a theorem of L. Guth [14] , the total number of self-intersections. Moreover, this lower bound is realized by an immersion! Therefore, for any immersion, the total number of self-intersections of the curve can be estimated in terms of the boundary-tangent -trajectories:

and for some special immersion, we get

Corollary 2.2 Let be a compact -manifold with boundary, which is properly contained in an

open -manifold. Let be a smooth map which is a immersion in the vicinity of the

boundary. Let be a Riemannian metric on which, in the vicinity of, is the pull-back of the Euclidean metric on.

Let be a linear function, and its composition with the map. Form the gradient field in. Assume that the pair is boundary generic in the sense of Definition 2.4.

For each, consider a -small tubular neighborhood of the manifold in. Then is an immersion. This setting gives rise to the Gauss map, defined by the

formula, where and is the unit vector inward normal to at.

Then the degree of the Gauss map can be calculated either by integrating (with respect to the

-measure) over the normal curvature of the hypersurface, or in terms of the

-induced stratum:

(4)

Proof. We will apply Theorem 2.4 to the field in to conclude that

Since in, , and the last term of this equation reduces to.

Remark 2.4. Of course, for an odd-dimensional, the Euler number, and so is. When is even-dimensional (i.e.,), the integral in Equation (4) can be expressed in terms of intrinsic Riemannian geometry of the manifold, namely, in terms of the Pfaffian. The Pfafian is a -differential form, whose construction utilizes the curvature tensor on the manifold (see [15] ). So, when,

Given a boundary generic field on, we introduce a sequence of basic degree-type invariants

which are intimately linked, via the Morse Formula (2), to the invariants.

We use a Riemannian metric on to produce the orthogonal projection of the field on the tangent subspace.

Let be the bundle of unit -spheres associated with the tangent bundle of the manifold. We denote by the restriction of the bundle to the subspace.

For each k, consider two fields, the inward normal field to in and, as sections of the sphere bundle (remember, is tangent to along so that along!). Assume that the sections ν and are transversal in the space. This transversality can be achieved by a perturbation of (equivalently, by a perturbation of the metric), supported in the vicinity of the singularity locus. Indeed, the intersections occur where the field is positively proportional to, that is, where. The later locus is exactly the locus. The perturbation does not affect the stratification. Assuming the transversality of the intersection, the locus is zero- dimensional.

We define the integer as the algebraic intersection number of two -cycles, and, in the ambient manifold of dimension.

Lemma 2.2 For a boundary generic field on a Riemannian manifold, the following formula holds:

Proof. We already have noticed that the intersection set projects bijectively under the map onto the locus, where the component of vanishes and points in- ward of. It takes more work to see that the sign attached to the transversal intersection point is, where is the index (the localized degree) of the field in the vicinity of its singularity. Thus. By the Morse Formula (2), the claim of the lemma follows.

Corollary 2.3 The integer depends only on the singular locus of and on the local indices of its points.

Question 2.1. How to compute in the terms of Riemannian geometry and in the spirit of Theorem 2.4 and Corollary 2.2?

For a boundary generic field and a fixed metric on, each manifold comes equipped with a preferred normal framing of the normal bundle: just consider the unitary inward normal field of in, then the unitary inward normal field of in, being restricted to, then the unitary inward normal field of in, being restricted to, and so on.

Via the Pontryagin construction [16] , this framing generates a continuous map. Its homotopy class is an element of the cohomotopy set. If, then we define to be the trivial map that takes to the base point in.

Unfortunately, as we will see soon,! However, when, each of the two loci is a closed manifold. Then we can apply the Pontryagin construction only to, say, to get a map. This application leads directly to the following proposition.

Corollary 2.4 Consider a boundary generic vector field such that and a metric, defined in the vicinity of in. Then these data give rise to continuous map.

The homotopy class is independent of the choice of and a homotopy of

within the open subspace of, defined by the constraint.

In particular, when, we get an element

and when, an element

If, we can interpret also as an element of the homotopy group.

The elements and have another classical interpretation as elements of oriented framed

cobordism set. In fact, the pair defines the trivial element in. In

contrast, if, then the bordism class may be nontrivial.

Let us recall the definition of framed cobordisms (for example, see [17] ). Let be oriented closed smooth -dimensional submanifolds of a compact -manifold, whose normal bundles and are equipped with framings and, respectively.

We say that two pairs and define the same element in, if there is a compact -dimensional oriented submanifold whose normal bundle admits a framing so that:

1),

2) the restriction of to coincides with, and the restriction of to coincides with.

Then the Pontryagin construction establishes a bijection, where. If both sets admit a structure of abelian groups and the bijection becomes a group isomorphism.

Now we are in position to explain why. Consider the obvious embedding

We can isotop in to a regular embedding

such that:

1), and

2) the inward normal field is parallel to the factor in the product.

Note that for, all the normal fields are preserved under the imbedding. So,

for any, the normal framing of in extends to a normal framing

of in. Therefore as an element of the framed bordisms of. As a

result, when, we get in (equivalently, in).

3. Deforming the Morse Stratification

Let be a smooth compact -manifold with boundary. A boundary generic field (see Definition 2.1) gives rise to two stratifications (1).

We are going to investigate how the stratification changes as a result of deforming the vector field.

Lemma 3.1 Let be a closed submanifold of a manifold and a closed manifold. Consider a family of maps such that each is transversal to. All the manifolds, maps, and families of maps are assumed to be smooth.

Then all the submanifolds are isotopic in. In particular, the intersections and are diffeomorphic.

Proof. Let be the map defined by the family. Thanks to the transversality hypothesis, is transversal to and is a submanifold of whose boundary is

Let be a vector field on, normal to each codimension 1 submanifold in. In the construction of, we evidently rely on the property of each being transversal to. Since and, each w-trajectory that originates at a point of must reach in finite time. Therefore, employing the w-flow, is diffeomorphic to, and the -image of that product structure in defines a smooth isotopy between and in. This isotopy extends to an ambient isotopy of itself [18] .

Note that these arguments fail in general if ether M or N have boundaries. However, under additional assumptions (such asbeing t-independent and), the relative versions of the lemma are valid.

Theorem 3.1 The diffeomorphism type of each stratum is constant within each path-connected component of the space of boundary generic fields.

Proof. If two generic fields, and, are connected by a continuous path, then they can be connected by a path such that the dependence of the field on is smooth. The argument is based on the property of generic fields to form an open set in the space of all fields (Theorem 2.1), the smooth partition of unity technique (which utilizes the compactness of manifold), and the standard techniques of approximating continuos functions with the smooth ones.

Thus it suffices to consider a smooth 1-parameter family of vector fields, connecting to. Since any generic field, viewed as a section of the vector bundle, is transversal its zero section, we may apply Lemma 3.1 (with, being the zero section of, , and) to conclude that all the submanifolds are isotopic in.

Since each divides into a pair of complementary domains, and, and since their polarity ±is determined by the inward/outward direction of, which changes continuously with, the ambient isotopy of (which takes to) must take to. The isotopy extends to an isotopy.

A similar argument applies to lower strata. Indeed, with the isotopy that takes to in place, consider the two sections, and, of the bundle

, both sections being transversal to the zero section of. Applying again Lemma 3.1, we conclude that the loci and are isotopic in (recall that these

loci are exactly the transversal intersections of two sections and of with its zero section).

Again, an isotopy that takes to must take to. The isotopy extends to an isotopy which preserves the pair. So, the pairs and are diffeomorphic via the composite isotopy.

This reasoning can be recycled to prove that all the pairs and are diffeomorphic via a single isotopy of. This argument is carried explicitly in the proof of Theorem 3.4 from [8] .

Corollary 3.1 Let be a -dimensional compact smooth manifold with boundary.

Within each path-connected component of the space of generic fields, the numbers, as

well as the numbers, are constant.

Proof. The claim follows instantly from Theorem 3.1 and Lemma 2.2.

For a manifold with nonempty boundary, by deforming any given function and its gradient-like field, we can expel the isolated -singularities from. This can be achieved by the appropriate “finger moves” which originate at points of the boundary and engulf the isolated singularities of. The result of these manipulations leads to

Lemma 3.2 Any connected -manifold with a non-empty boundary admits a Morse function with no critical points in the interior of and such that is a Morse function. Such functions form an open nonempty set in the space of all smooth functions on.

As a result, the gradient-like vector fields on form an open nonempty set in the space of all vector fields on.

Proof. Let us sketch the main idea of the argument. Start with a Morse function. Connect each critical point in the interior of by a smooth path to a point on the boundary in such a way that a system of non-intersecting paths is generated. Then delete from small regular neighborhoods of those paths (“dig a system of dead-end tunnels”) and restrict to the remaining portion of. Smoothen the entrances of the tunnels so that the boundary of will be a smooth manifold which is diffeomorphic to. We got a nonsingular function on. A slight perturbation of on will not introduce critical points in the interior of and will deliver a Morse function on its boundary. Indeed, recall that the sets of Morse functions on and are open and dense in the spaces and of all smooth functions, respectively (for example, see [9] ). Of course is an open condition imposed on a vector field on a compact manifold. On the other hand, if, then any field, sufficiently close to, will have the property. The previous arguments show that the set of gradient-like non-vanishing fields is nonempty. So it is an open nonempty subspace in the space of all all vector fields on.

Eliminating isolated critical points of a given function on a manifold with boundary is not “a free lunch”: the elimination introduces new critical points of the restricted function. This is a persistent theme throughout our program:

Expelling critical points of gradient flows from a manifold leaves crucial residual geometry on its boundary.

This boundary-confined geometry allows for a reconstruction of the topology of.

Ideas like these will be developed in the future papers from this series. Meanwhile, the following lemma gives a taste of things to come.

Lemma 3.3 Let be a Morse function with no local extrema in the interior of a -manifold. Then an elimination by a finger move5 of each -critical point of the Morse index results in the introduction of new critical points of positive type and new critical points of negative type for the modified function.

Proof. Let be a Morse singularity of in the interior of. Denote by a sphere which bounds a

small disk centered on and such that is a Morse function. Without loss of generality, we can

assume that, in the Morse coordinates, is given by, while with all the being distinct. Then has only Morse-type singularities at the points where the coordinate axes pierce the sphere. With respect to the pair, these points come in two flavors: positive and negative. The two types are separated by the hypersurface of the cone

In the vicinity of, the intersection is exactly the locus

so that the -gradient field (tangent to along) is transversal to, the product of two spheres. Therefore, in the vicinity of,!

The function has exactly critical points of the positive type and exactly

critical points of the negative type. We shall denote these sets by and the two domains in which divides―by.

Let be a local maximum of. Note that it is possible to connect to a non-singular (for) point by a smooth path along which f is increasing. Indeed, any non-extendable path such that either approaches a critical point or reaches the boundary. By a small perturbation, we can insure that avoids all the (hyperbolic) critical points in the interior of X (by the hypothesis, f has no local maxima/minima in the interior of X). Thus can be extended until it reaches the boundary at a point.

Drilling a narrow tunnel, diffeomorphic to the product, along does not change the topology of X; the function retains almost the same list of singularities at the boundary as the function has: more accurately, the local maximum at disappears in and a negative critical point of index 1 of appears near the -end of the tunnel. Thus we have modified f and have eliminated the critical point in the interior of X at the cost of introducing on the boundary critical points of positive type and critical points of negative type.

Soon, motivated by Lemma 3.2, we will restrict our attention to nonsingular functions and their gradient-like fields―an open subset in the space of all gradient-like pairs; but for now, let us investigate a more general case.

Consider Morse data, where the field is nonsingular along the boundary. Extend to and, where C is some external collar of so that the extension is nonsingular in C. At each point, the -flow defines a projection of the germ of into the germ of the hypersurface.

Let and denote the pure strata and, respectively. At the points, is a surjection; at the points of, it is a folding map; at the points, it is a cuspidal map. Often we will refer to points by the smooth types of their -projections.

As the theorem and the corollary below testify, for a given function, we enjoy a considerable freedom in changing the given Morse stratification by deforming the -gradient-like field (cf. Section 3 in [5] ).

Theorem 3.2 Let be a compact smooth -manifold with nonempty boundary. Take a smooth function with no singularities along, and let be its gradient-like field. Consider a stratification

of X by compact smooth manifolds, and let and denote the critical sets of the restrictions and, respectively. Assume that the following properties are satisfied:

・ ,

・ and are regular embeddings for all,

・ for each the functions and have Morse-type critical points at the loci and, respectively,

・ at the points of, and, at the points of, , where is the inward normal to in 6.

Then, within the space of -gradient-like fields, there is a deformation of into a new boundary generic gradient-like field, such that the stratification, defined by, coincides with the given

stratification.

Proof. We pick a Riemannian metric g in a collar U of in X so that becomes the gradient field of f. Consider auxiliary vector fields, where denotes the orthogonal projection of on the tangent spaces of closed manifold.

The construction of the desired field is inductive in nature, the induction being executed in increasing values of the index. Figure 4 illustrates a typical inductive step.

Assume that has been already constructed so that and for all. This assumption implies that is tangent to exactly along its boundary for all. Along

(and thus along), we decompose as, where

.

The idea is to modify in the direction normal to in, while keeping the rest of its components unchanged.

Denote by the tangent space of at. Let be the open half-space of positively

spanned by the vectors that point inside of. Let be half of the tangent space, defined by, where. We introduce the complementary to and open half-spaces and.

At each point, consider the open cone and, at each point, the open cone (see Figure 4). These cones are non-empty, except perhaps at the points of, where is anti-parallel to the inward normal of. However, at, , and at, due to the last bullet in the hypotheses of the theorem. Thus, for each, there is a number h so that the vector (this conclusion uses the the property on the set). Similarly, for each, there is a number h so that. By the partition of unity argument, which employes convexity of the cones, there is a smooth function which delivers the desired field u_k along. In order to insure the continuity of h and across the boundary, we require. Thus on.

Put. Now, for all (these strata depend on the’s only),

and by the construction of. Moreover, for all. In fact, is tangent to along. Note that this inductive argument should be modified for since is 0-dimensional.

We smoothly extend into a regular neighborhood V of in X. Abusing notations, we denote this extension by as well. The neighborhood is chosen so that there.

To complete the proof of the inductive step, we form the field, where the functions deliver a smooth partition of unity subordinate to the cover of X. Since defines a convex cone in the space of vector fields, is a f-gradient-like field with the desired Morse stratification.

Theorem 3.2 has an immediate implication:

Corollary 3.2 Let be a Morse function and its boundary generic gradient-like field with the

Morse stratification. Assume that compact codimension zero submanifolds

are chosen so that, for each, and.

Then, within the space of f-gradient-like fields, it is possible to deform into a new gradient-like boundary generic field, such that the stratification coincides with the given stratification.

Moreover,.

In particular, if, the claim is valid for any stratification as above that terminates with.

The next proposition (based on Corollary 3.2) shows that, for a given Morse function, by an appropriate choice of gradient-like field, the Morse stratification can be made topologically very simple and regular: namely, each stratum is a disjoint union of -dimensional disks. Moreover, when the boundary is connected and, each stratum is a just a single disk.

Corollary 3.3 Let be a Morse function on a compact -manifold, being nonsingular along the boundary. We divide the connected components of the boundary into two types, A and B. By definition, for type A, the singularity set, and for type B,.

Then any f-gradient-like field can be deformed, within the space of f-gradient-like fields, into a boundary generic field so that, for each component of type A and all, the stratum is diffeomorphic to a disk. At the same time, for the components of type and all, the stratum.

For the components of type, in contrast, the 1-dimensional stratum is a finite union of arcs residing in the circle. Moreover, , the number or arcs in, and the number of points in are linked via the formula

, whereis the index of the field, and is the number of boundary components of type.

Proof. If, for each type A connected component of, the singularity set can be included in a disk. By Corollary 3.2, we can deform to a new -gradient-like field, so that the new stratum. If, then the singularity set can be incapsulated in a disk. By the same token, after still another deformation of, we can arrange for and. This process repeats itself, unless the dimension of becomes one. At its final stage, consists of several arcs which are contained in the circle.

For each type connected component of, by a similar reasoning, we can arrange for. Thus, for all and.

Therefore, letting for all in Corollary 3.2, we have established all the claims of the corollary, but the last one.

Since and both are the gradient-like fields for the same Morse function, their indexes, and, are equal. Thus we get

, where is the contribution of all the disk-shaped strata to the Morse Formula (2).

Recall that, by Corollary 4.4 [5] , for any 3-fold and a boundary generic field on it, we get, provided. Thus, as a positive increases, the boundary of the disk becomes more “wavily”.

For example, by attaching many 2-handles to the boundary of a 2-disk, we get a 2-fold X with a big value of. On such, for any gradient-like field such that.

These examples motivate the following question.

Question 3.1 For boundary generic gradient-like fields with a fixed value of the index and a

disk-shaped stratification as in Corollary 3.3, what is the minimum of?

Evidently, such number is an invariant of the diffeomorphism type of. It seems that is semi-additive under the connected sum operation: that is,

4. Boundary Convexity and Concavity of Vector Fields

We are ready to introduce pivotal concepts of the stratified convexity and concavity for smooth vector fields on manifolds with boundary.

Definition 4.1 Given a boundary generic vector field (see Definition 2.1), we say that is boundary -convex, if. In particular, if, we say that is boundary -convex, or just boundary convex.

We say that is boundary s-concave, if. In particular, if, we say that is boundary 2-concave, or just boundary concave.

Example 4.1. Assume that a compact manifold X is defined as a 0-dimensional submanifold in the interior of a Riemannian manifold, given by an inequality, where is a smooth function with 0 being a regular value. Then the boundary convexity of a gradient field in X can be expressed in terms of the Hessian matrix by the inequality

at all points, where is tangent to. If

, where is tangent to, then the field is boundary concave.

Example 4.2. According to the argument in Lemma 3.3, the complement to a small convex (in the Morse coordinates) disk, centered at a Morse type -critical point, is boundary concave with respect to the gradient field. In fact, the field is both boundary 3-concave and 3-convex! So, if is a Morse function on a closed manifold Y with a critical set, then the complement X in Y to a small locally convex neighborhood of admits a boundary concave -gradient-like field (with)!

Theorem 4.1 below belongs to a family of results which we call “holographic” (see also and Theorem 4.2). The intension in such results is to reconstruct some structures on the “bulk” (or even the space itself) from the appropriate flow-generated structures (“observables”) on its boundary. A paper from this series will be devoted entirely to the phenomenon of holography for nonsingular gradient flows.

In Theorem 4.1, we describe how some boundary-confined interactions between the critical points of a given function of opposite polarities can serve as an indicator of the convexity/concavity of the gradient field in X (recall that the convexity/concavity properties of the -flow do require knowing the field in the vicinity of in X!).

Theorem 4.1 Let, be Morse functions and and their gradient fields with respect to a Riemannian metric on X and its restriction to, respectively. Assume that is boundary generic.

If, then there is no ascending -trajectory, such that

(both critical sets depend only on).

Conversely, if for a given -gradient pair, no such -trajectory exists, then one can deform to a new boundary generic pair of the -gradient type so that. Moreover, the fields and on can be chosen to be arbitrary close in the -topology.

In particular, if (as sets), then X admits a boundary generic and convex f-gradient-like field

; similarly, if, then X admits a boundary generic and concave f-gradient-like field.

Proof. First consider the convex case, that is, the relation between the property and the absence of an ascending -trajectory which connects to.

Consider the function, defined via the formula, where denotes a unitary field inward normal to in. Since is boundary generic, zero is a regular value of. Then

and.

If an ascending -trajectory, which links with, does exist, it must cross somewhere the boundary of. Since the field is an orthogonal projection of on, the two fields must agree at any point―the locus where is tangent to. Thus, is the gradient of at. Therefore, as crosses from into at, in its vicinity, the arc lies below the arc (see Figure 5). By the definition of the locus, such crossing belongs to. Therefore, , contrary to the theorem hypothesis.

On the other hand, if no such -trajectory exists, then we claim the existence of a codimension one closed submanifold, which separates in two manifolds, and , such that the vector field, or rather its perturbation, is transversal to and points outward of. Indeed, for each critical point, in the local Morse coordinates on, consider a small closed

-disk centered on the critical point x. Denote by the closure of the union of downward trajectories of the -flow passing through the points of (see Figure 6, the left diagram). Let be the union (see Figure 6, the right diagram).

Since we assume that no descending -trajectory links a point of to a point of, we can choose

the disks so small that the set belongs to the complement.

For each, the zero cone of the Morse function separates the sphere

into two handles, and (each being a product of a sphere with a disk). We denote by the handle in whose spherical core is formed by the intersection of the unstable disk through with the sphere. Then, by definition, the set is a collection of downward trajectories through the points of union with. Note that the downward trajectories from a different set could enter the disk only through the complementary handle in its boundary. As a result, is a manifold whose piecewise smooth boundary could have corners (see Figure 6, the right diagram). Similarly, is a domain in whose boundary is piecewise smooth manifold with corners.

Since consists of the downward trajectories of, if, then any point which can be reached from following the field (for short, “is below”) belongs to as well. Therefore the boundary is assembled either from downward trajectories or from singletons; the singletons are contributed by some portions of where points outside of the relevant disk. Thus either is tangent to, or it points outside.

Away from, is of the -gradient type. Thus, in each tangent space, where, there is an open cone comprised of -gradient type vectors, and. Therefore, in the vicinity of, we can perturb to a new field of the -gradient type, so that points strictly outside and still for all. It is possible to smoothen the boundary so that, with respect to a new smooth boundary, the field still points outside, the new domain bounded by, and for all.

Note that if, then can serve as a separator.

Let and. With the separator in place, consider a smooth function with the properties:

1) zero is a regular value of, and,

2), ,

3) in a neighborhood of,

4), where is the inward normal to in.

Note that the field points inside of along and outside of along. It also points outside of along. As a result, we conclude that and; in other words, is boundary convex. Note that can be chosen arbitrary close to. Ineeded, employing Theorem 3.2, we can perturb to insure its genericity with respect to the pair, and thus the boundary genericity of itself.

The argument in the concave case, which deals with the relation between the property and the absence of an ascending -trajectory, connecting to, is analogous. We just need to switch the polarities of the relevant sets.

Now we need to introduce a number basic notions to which we will return on many occasions in the future.

Definition 4.2 Let be a differential -form on a manifold.

We say that a path is -positive (-negative), if, for all values of the parameter.

Definition 4.3 Let be a closed differential 1-form on a manifold, equipped with a Riemannian metric. We say that a vector field on is the gradient of (and denote it “”), if for any vector field on.

Definition 4.4 Let be a differential 1-form on a manifold Y and let be the set of points, where is the zero map. Assume that for some smooth function in the vicinity of.

We say that a vector field is of -gradient type if on and in the vicinity of. Here is some Riemannian metric in the vicinity of (cf. Definition 2.2).

We are in position to formulate a generalization of Theorem 4.1 for closed differential -forms―another instance of somewhat weaker “holographic phenomenon”, this time for fields which may not be gradient-like globally.

Theorem 4.2 Let be a closed 1-form on a compact manifold, equipped with a Riemannian metric. Assume that and have only Morse-type singularities. Let the gradient be a boundary

generic field, and let.

If, then there is no -ascending -trajectory, such that

Assume that there exists a codimension one submanifold, which separates and and such that the field is transversal to and points outwards/inwards of the domain in that is bounded by and contains. Then one can deform the -gradient vector fields to a new boundary generic pair of the -gradient type so that.

Proof. The -gradient fields on are characterized by the property, valid on the

locus where. Usually, in this setting, we do not have a natural choice for the wall which would separate the singularities of opposite polarities and and such that the field would be transversal to N. It seems unlikely that the absence of an ascending -trajectory which links with is sufficient to guarantee the existence of a separator N. However, in the presence of such separator N, the arguments are identical with the ones employed in the proof of Theorem 4.1.

Remark 4.1. In Theorem 4.1 and Theorem 4.2, the partition of the singular set must satisfy some basic relations:

These relations reflect the fact that when, and when.

Given a metric on a Riemannian -manifold, let us recall a definition of the Hodge Star Operator (see [19] ).

Pick a local basis of 1-forms in and consider the associated basis

of, where and the symbol “ “ stands for omitting the -th form from the product.

Assume that, in the dual to basis of, the metric is locally given by a matrix. Then the matrix of the -operator in the bases, is given by the formula

(5)

whence.

Definition 4.5 A closed differential 1-form on a compact manifold Y is called intrinsically harmonic if there exists a Riemannian metric g on Y such that the form is closed.

Example 4.3. Let be a closed smooth manifold and a smooth map with isolated Morse-type singularities. Consider the closed -form, the pull-back of the canonic 1-form on the circle. Assume that one of the -fibers, , is connected. Then is intrinsically harmonic [20] .

Let denote the singularity set of a closed 1-form on a compact manifold Y. We assume that.

By Calabi’s Proposition 1 [19] , is intrinsically harmonic if and only if through every point there is a -positive path which either is a loop, or which starts and terminates at the boundary.

Theorem 4.3 Let be a closed -form on a Riemannian manifold, such that. Assume that, the restriction of to, is a harmonic form7.

Then the gradient field is not boundary convex or boundary concave (that is, and). Thus, if is connected, then.

Proof. We abbreviate to and to. Here is the *-operator on the boundary of X

with respect to the given Riemannian metric on.

If is a closed -form on, then by the Stokes Theorem,

However, for a concave/convex gradient field, the -form, being restricted to, is proportional to the volume form of with negative/positive functional coefficient. Indeed, at the points of, the angle between and the normal to in is acute, while it is obtuse at the

points of. Therefore, when either or. The resulting contradic-

tion proves that and.

Therefore, when is connected, then and must share the common nonempty boundary―the gradient field must have cuspidal points.

Example 4.4. Let be a compact smooth manifold and a smooth map with isolated Morse- type singularities. Consider the closed -form, the pull-back of the canonic 1-form on the circle. Assume that one of the fibers of the map is connected. Then there exists a metric

on such that the form is harmonic ([19] [20] ). Consider the gradient field.

Then by Theorem 4.3, and for any metric that “harmonizes”.

Definition 4.6 A non-vanishing vector field on a compact manifold is called traversing if each -trajectory is either a closed segment or a singleton which belongs to.

Remark 4.2. The definition excludes fields with zeros in (they will generate trajectories that are homeomorphic to open or semi-open intervals) and fields with closed trajectories. Note that all gradient-like fields of nonsingular functions are traversing, but the gradient-like fields of nonsingular closed 1-forms may not be traversing!

Lemma 4.1 Any traversing vector field is of the gradient type.

Proof. Let be a traversing field on X. We extend the pair to a pair so that X is properly contained in and.

Then every -trajectory has a local transversal compact section of the -flow. We can choose to be diffeomorphic to a n-dimensional ball with its center at the singleton. We denote by the union of -trajectories through.

For each -trajectory, there exists a section so that the set contains a compact cylinder

, where are positive constants (which depend on), with the properties:

1),

2) for any -trajectory through, the intersection is a segment,

3) the point belongs to the interior of segment.

Then the collection forms a cover of. Since is compact, we can choose

a finite subcover of.

For each and the corresponding section, we produce a smooth function by integrating the vector field and using as the initial location for the integration.

More accurately, let

be the parametrization of a typical trajectory , such that

for all and . This bijective parametrization introduces a smooth product structure

by the formula .

We define a smooth function by the formula and denote it (quite appropriately)

by the symbol .

Let be a smooth non-negative function that vanishes only on the boundary . Let

denote the composition of the -directed projection with the function

. Since vanishes on , the function extends smoothly on X to produce a smooth function

with the support in .

Now consider the smooth function

(6)

It is well-defined on X. Let us compute its-directional derivative:

(7)

Let us explain Formula (7). By the very definition of , it is constant on each-trajectory, so that

. Also, in . At the same time, , since and

increases in the direction of . Finally, each belongs to the interior of some set .

Therefore, , so that is a gradient-like field for .

Corollary 4.1 Let X be a smooth compact manifold with boundary. Then ―the space of traversing vector fields on X―is nonempty and coincides with the intersection , where denotes the space of gradient-like fields, and the space of all non-vanishing fields on X.

Proof. By definition, any traversing field on X does not vanish. By Lemma 4.1, must be of the gradient type. Thus

On the other hand, for a compact X with a gradient-like , each -trajectory through must reach the boundary in both finite positive and negative times (since it is controlled by some Lyapunov function f).

As a result,

It remains to show that . By Lemma 3.2, , which implies that .

There are simple topological obstructions to boundary convexity of any gradient-like nonvanishing field on a given manifold X. The next lemma testifies that the existence of boundary convex traversing fields imposes severe restrictions on the topology of the manifold X.

Lemma 4.2 A connected -manifold X admits a boundary convex traversing8 field , if and only if, X is diffeomorphic to a product of a connected compact n-manifold and a segment, the corners of the product being smoothly rounded.

Proof. Indeed, if such convex exists, must be a deformation retract of X: just use the down flow to produce the retraction. Therefore, when , then X is homeomorphic to the quotient space

, where the equivalence relation “” is defined by collapsing each segment

to a point. If we round the corners generated in the collapse, we will get a diffeomorphism between X and the “lens” (see Figure 7).

On the other hand, any product , whose conners being rounded, admits a field of the desired boundary convex type.

Corollary 4.2 For all , any smooth compact contractible -manifold X, which admits a boundary convex traversing field, is diffeomorphic to the standard -disk.

Proof. By Lemma 4.2, X is diffeomorphic to a product of a fake -disk Y with , the corners of the product being rounded.

For , by Perelman’s results [21] [22] , Y is diffeomorphic to the standard 3-disk. Thus X is diffeomorphic to the standart 4-disk.

For , we do not know whether Y is a standard 4-disk.

For , the h-cobordism theorem [23] implies that any fake n-disk is diffeomorphic to the standard disk.

This leaves only the case of 5-dimensional X wide open.

We notice that is an obstruction to finding boundary convex traversing on a -dimensional manifold with a connected boundary.

Corollary 4.3 Let X be a smooth connected compact -manifold with boundary, which admits a boundary convex traversing field.

If , then X is diffeomorphic to the product , where Y is a closed manifold.

In particular, no connected X with boundary , whose number of connected components differs from two, and with the property admits a boundary convex traversing field.

Proof. If such boundary convex traversing field exists, must be a deformation retract of X. Therefore, for a connected X, must be connected as well.

On the other hand, if , then the connected must be of a homotopy type of a -dimensional complex. In such a case, the groups must vanish.

Thus when and is boundary convex, the only remaining option is , which implies that ―the manifold is closed. In such a case, X is a product of a connected closed -manifold with an interval; so the boundary must be the union of two diffeomorphic components.

As with the boundary convex traversing fields, perhaps, there are topological obstructions to the existence of a boundary concave traversing field on a given manifold? At the present time, the contours of the universe of such obstructions are murky. We know only that the disk does not admit a non-vanishing boundary concave field (see Example 4.4).

Lemma 4.3 If a boundary generic vector field on an even-dimensional compact orientable manifold is boundary concave, then its index

If a boundary generic vector field on an odd-dimensional compact orientable manifold X is boundary concave, then its index

Thus, for all boundary concave fields with a fixed value of index , the Euler number is a topological invariant.

Proof. For a boundary concave field , . Therefore, the Morse Formula (2) reduces to the equation

(8)

Recall that, for any orientable odd-dimensional manifold Y, . Therefore, when , we get . Thus formula (8) transforms into

For an odd-dimensional X, the closed manifold is odd-dimensional, so . Therefore

.

Corollary 4.4 Let X be a -dimensional oriented smooth and compact manifold with boundary.

If , then for any boundary generic concave vector field on X of index 0, the locus contains at least two-dimensional spheres.

Proof. Since is a closed orientable 2-manifold, its Euler number is positive only if contains sufficiently many 2-spheres. By Lemma 4.3, . Therefore contains at least two-dimensional spheres.

Example 4.4. Let , the 2-dimensional ball. If on X, then by the Morse formula,

If consists of k arcs, then by this formula, . At the same time, . Therefore, . So we conclude that does not admit a non-vanishing field with , that is, a boundary concave field.

At the same time, if we delete any number of disjoint open disks from , the remaining surface X admits a concave non-vanishing gradient-like field: indeed, consider the radial field in an annulus A and delete from A any non-negative number of small round disks. The radial field on A, being restricted to X, is evidently of the gradient type and concave with respect to .

Note that, if a connected compact surface X admits a generic traversing concave field , then X is homeomorphic either to a thickening of a finite graph whose vertexes all have valency 3, or to an annulus.

In the previous example, we have seen that the disk does not admit a non-vanishing concave field. In contrast, does admit a boundary generic concave non-vanishing field: just consider the restriction of the Hopf field on to the northern hemisphere . For the unitary disk centered at the origin, informally, we can describe as the sum of the velocity field of the solid , spinning around the -axis, with the solenoidal field of the loop . However, this field is not of the traversing type: it has closed trajectories (residing in the solid torus ).

These observations encourage us to formulate

Conjecture 4.1 The standard -diskdoes not admit a traversing boundary concave vector field.

The construction of a boundary concave field on a 2-disk with holes (see Example 4.4) admits a simple generalization.

Example 4.5. Consider a closed -manifold Y. Let be compact submanifolds also of dimension . Let . We pick disjointed close intervals in the interval . Then we form the product . By rounding the corners of , we get a -manifold so that each segment , where , hits along a closed segment, and each segment , where , hits along a singleton.

Form the manifold . Its boundary consists of two copies of Y together with the disjoint union of (they are the doubles of ’s). The obvious vertical field on W, being restricted to X, is boundary

concave. In fact, , where , and .

These examples lead to few interesting questions:

Question 4.1. Which compact manifolds admit boundary concave non-vanishing vector fields? Which compact manifolds admit boundary concave non-vanishing gradient-like fields?

Despite the “natural” flavor of these questions, we have a limited understanding of the general answers. Nevertheless, feeling a bit adventurous, let us state briefly what kind of answer one might anticipate. This anticipation is based on a better understanding of boundary concave traversing fields on 3-folds (see [5] [24] ).

We conjecture that an -dimensional X admits a traversing concave field such that

if (perhaps, if and only if) X has a “special trivalent” simple -dimensional spine, where denotes a smooth triangulation of X (see [25] for the definitions of simple spines and for the description of their local topology). Here “special trivalent” means that each -simplex from the singular set SK of K is adjacent to exactly three -simplexes from K. Moreover, the vicinity of SK in K admits an oriented branching as in [24] .

When the -manifold in question is specially manufactured from a closed -manifold by removing a number of -disks, another paper from this series will provide us with a wast gallery of manifolds which admit traversing concave fields.

5. Morse Stratifications of the Boundary 3-Convex and 3-Concave Fields

We have seen that the boundary 2-convexity of traversing fields on X has strong implications for the topology of X (for example, see Lemmas 4.2 - 4.3, and Corollaries 4.2 - 4.4).

By itself, the boundary 3-convexity and 3-concavity of traversing fields has no topological significance for the topology of 3-folds: we have proved in Theorem 9.5 from [5] that, for every 3-fold X, any boundary generic of the gradient type can be deformed into new such field with. However, in conjunction with certain topological constraints on (like being connected), the boundary 3-convexity has topological implications (see [5] , Corollary 2.3 and Corollary 2.5).

These observations suggest two general questions:

Question 5.1.

・ Given a manifold X, which patterns of the stratifications are realizable by boundary generic traversing fields on X?9

・ Given two such fields, and, can we find a linking path in the space that avoids certain types of singularities?1⁰ Specifically, if for some, , is there a linking path so that for all?

Remark 5.1. The property of the field in Question 5.1 being traversing (equivalently, boundary generic and of the gradient type) is the essence of the question. For just boundary generic fields, there are no known restrictions on the patterns of.

Let us illustrate this remark for the fields such that. We divide the boundary into two complementary domains, and, which share a common boundary―a closed manifold of dimension. It may have several connected components. Next, we divide the manifold into two com- plementary closed manifolds and.

We claim that it is possible to find a boundary generic field with the properties:, , and. The construction of such is quite familiar (see the arguments in Theorem 3.2).

We start with a field which is normal to and points outside of along and inside of along. We extend to a field tangent to the boundary so that has only isolated zeros. Let be the outward normal field of in X and a smooth function such that 0 is its regular value and

Along, form the field and extend it to a field on X with isolated singularities in. By its construction, has all the desired properties. Note that here we do not insist on the property.

In our inquiry, we are inspired by the Eliashberg surgery theory of folding maps [6] [7] . In many cases, Eliashberg’s results give criteria for realizing given patterns of, provided that, thus answering Question 5.1. Let us state one such result, Theorem 5.3 from [7] .

Theorem 5.1 (Eliashberg) Let, , be a compact connected smooth submanifold of dimension. Consider two disjoint closed and nonempty -submanifolds and of whose union separates into two complementary -manifolds, and. Let be the outward normal field of in X, and denote by the degree of the Gauss map. Let be a linear surjection.

Then the topological constraints

・ , when

・ , when

are necessary and sufficient for the existence of an orientation-preserving diffeomorphism with the following properties:

・ is the fold locus of the map,

・ , being restricted to, is a immersion, and the image has only transversal self-intersections in,

・ the differential takes the normal field to the field inward normal to in,

・ the differential takes the normal field to the field outward normal to in.

Considering a traversing field which is tangent to the fibers of the map from Theorem 5.1, leads instantly to

Corollary 5.1 Under the hypotheses and notations from Theorem 5.1, there exists a boundary generic traversing field on so that:

・ ,

・ ,

・ .

Thus, at least for smooth domains and for boundary generic traversing fields, which are both 3-convex and 3-concave, the patterns for the strata

are indeed very flexible. However, the requirement that both and puts breaks on any applcation of Corollary 5.1 to boundary concave and boundary convex traversing fields on!

Example 5.1. Let us illustrate how non-trivial the conclusions of Theorem 5.1 and Corollary 5.1 are. Let,. When is odd, take any codimension one submanifold such that, , and. Then admits a boundary generic traversing field such that and.

For instance, admits a a boundary concave traversing field such that, the orientable surface of genus 2, and, the 2-torus.

When is even, take any codimension one submanifold such that, , and. Then admits a boundary generic traversing field such that and.

For example, for any collection of loops, , , the disk admits a boun-

dary generic traversing field such that and.

We suspect that an important for our program generalization of Theorem 5.1 is valid and can be established by the methods as in [6] [7] .

Conjecture 5.1 Let be a compact connected smooth manifold of dimension, equipped with a traversing vector field. Let and be two disjoint closed and nonempty -submanifolds of whose union separates into two -manifolds, and.

Then the topological constraints

(9)

(10)

are necessary and sufficient for the existence of an orientation-preserving diffeomorphism with the following properties:

・ the restriction of to the image is boundary generic in the sense of Definition 2.1¹¹,

・ ,

・ ,

・ .

Moreover, in a given collar of in, there is a -supported diffeomorphism as above which is arbitrary close in the -topology to the identity map.

To prove the necessity of the topological constraints (9) and (10) is straightforward. By the Morse Formula (2) (see also Corollary 5.1), a necessary condition for the existence of a diffeomorphism with the desired properties, described in the bullets, is the constraint

Since is a homeomorphism, this equation is equivalent to

(11)

If, then

Therefore, using Formula (11), the constraint becomes―Formula (10).

When, since are closed odd-dimensional manifolds, , Formula (11) reduces to―Formula (9).

Therefore the topological constraints (9) and (10) imposed on the “candidates”, and and are necessary for the existence of the desired diffeomorphism.

To prove the sufficiency of these conditions may require a clever application of the -principle in the spirit of [6] [7] .

Corollary 5.2 Assuming the validity of Conjecture 5.1, any compact smooth manifold with boundary admits a boundary generic traversing field with the property.

Proof. By Corollary 4.1, , we can start with a traversing field and apply Conjecture 5.1 to it to get the pull-back field with the desired properties.

Conjecture 5.2 Given two vector fields and as in Corollary 5.2, there is a 1-parameter family of traversing fields which connects to and such that only for finitely many instances,. For those exceptional’s,.

Cite this paper

GabrielKatz, (2014) Stratified Convexity & Concavity of Gradient Flows on Manifolds with Boundary. Applied Mathematics,05,2823-2848. doi: 10.4236/am.2014.517270

References

NOTES

¹in the sense of Definition 2.4

² By definition, and.

³Thus is a transfer by of the constant field.

⁴Recall that.

⁵as in the proof of Lemma 3.2.

⁶This condition is metric-independent: it does not depend on the choice of.

⁷This assumption implies that, provided.

⁸equivalently, a non-vanishing gradient-like field.

⁹Theorem 5.1 and Corollary 5.1 below give just a taste of a possible answer.

¹⁰When, Theorem 9.5 in [5] addresses some of these questions.

¹¹and even traversally generic in the sense of Definition 3.2 from [8]