Received 26 May 2014; revised 2 July 2014; accepted 14 July 2014

ABSTRACT

We discuss a new possible construction of the regular heptagon by rhombic bicompasses ex- plained in the text as a new geometric mean of constructions in the spirit of classical constructions in connection with an unmarked ruler (straightedge). It avoids the disadvantages of the neusis construction which requires the trisection of an angle and which is not possible in classical way by compasses and ruler. The rhombic bicompasses allow to draw at once two circles around two fixed points in such correlated way that the position of one of the rotating points (arms) on one circle determines the position of the points on the other circle. This means that the positions of all points (arms) on both circles are determined in unique way.

Keywords:

Plane Geometry, Algebra, Geometric Constructions, Heptagon, Cyclotomic Equations, Neusis

1. Introduction

It is well known that the regular heptagon is the first in the series of regular 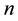-polygons which cannot be constructed by compasses and ruler (e.g., [1] - [8] ). The neusis construction [3] [8] is, in principle, an exact construction but it requires the trisection of an angle which is not possible by compasses and ruler alone. This makes it necessary to fit a distance markable on a ruler (straightedge) between a line and a circle in such a way that the ruler finally intersects a given point on the circle and a new point on the line which last marks the vertex of the trisected angle. We describe in this paper a new exact construction by a mean which we call rhombic bicompasses in connection with a ruler. The rhombic bicompasses can be fixed to arbitrary two points and the arms possess then one degree of freedom which allow them to describe two circles in correlated way. The position of a point on one circle determines then at once the positions of all other movable points on the two circles. It is important that in case of the regular heptagon, the relative coordinates of the fixed points are geometrically constructible since they are given only by rational numbers together with a square root of a natural number. We explain this in Section 3 and give the formulae for the coordinates of the correlated movable points of the bicompasses in dependence on the two fixed points in an Appendix A.

2. Circle Division and Factorizations of Cyclotomic Equation for Regular Heptagon

The regular heptagon with significant points for our construction method which we describe in the following is shown in Figure 1.

The points 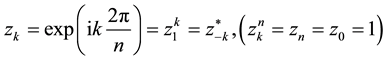which solve the cyclotomic equation

and thus the circle division problem (we set radius) determine the corners of the regular heptagon in case of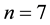. The corresponding palindromic polynomial of 6th degree which determines the primitive roots

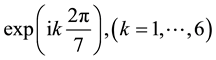is represented in the usual approach [1] in the following way [1] [6] [7]

(1)

The solution of the obtained cubic equation for 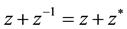by the formulae of Cardano provides the Cosines of the angles to the points 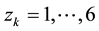according to

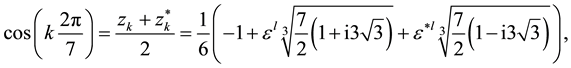(2)

where 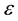denotes the cubic roots of as follows

(3)

and where the two cubic roots in (2) are to take as complex conjugate ones (which ones can change the assignment to on left-hand side). An analogous approach of separation of an equation for of degree is possible for arbitrary odd and in modified form for arbitrary even.

Another approach with factorization of the polynomial of 6-th degree of the cyclotomic equation for into two cubic polynomials although not in the field of rational coefficients but in an extension by complex number is the following

(4)

It comprises in one cubic factor the 3 cubic roots and in the other cubic factor the 3 complex conjugate roots (see Figure 1). One can easily check the factorization (4) but one can derive the possibilities also in a systematic way. In the systematic way for arbitrary prime number (e.g., [5] [6] [9] ) one takes an arbitrary primitive root and forms then sequences of powers

of up to the moment when due to these sequences return to

the chosen initial element as follows

(5)

This happens with necessity latest after steps since the root forms its own sequence with only one element and due to the construction which guarantees that all roots of two sequences are different from each other or one has the same sequence in a different cyclic order of the roots. In our case of three-root cycles and one finds from that the last coefficient in the factorized polynomials of degree 3 is equal to and from and that the first and se-

cond coefficient are negative complex conjugate with real part equal to and it remains to determine only

an imaginary part in the first and second coefficient that is easily to find from the product of the factors.

A further difference between the type of polynomial in Equation (1) and the type of polynomials in the factorization in (4) is, as already mentioned, that the coefficients of the corresponding polynomials are rational (field) in first case and complex irrational in second case (more specially of the form with complex rational and integer). However, this is not important for the considered solutions in radicals by the formula of Cardano which in both cases belong to the field and the involved cubic roots are complex numbers belonging to the “Casus irreduciblis” (e.g., [9] ). The solution of the two cubic equations (4) by the formulae of Cardano provides for (with correspondences)

(6)

and for (with correspondences)

(7)

where again denotes the cubic roots of according to (3). For the cubic roots in each of the formulae (6) and (7) one has to take the same (but arbitrary) of the 3 possible values that is the reason that we do not transform them into the numerator¹.

Other factorizations than (4) involving 3 of the roots, for example and, do not lead to cubic polynomials with coefficients containing only square roots of the form with from but contain higher-order roots for which last the sum of the 3 roots is then not constructible by compasses and ruler.

3. Rhombic Bicompasses and Geometrical Construction of the Regular Heptagon

We describe now a new device in the spirit of classical geometrical constructions by compasses and ruler and suggest to call it rhombic bicompasses. It is schematically shown in Figure 2 on the left-hand side. It consists of 12 arms of equal length 1 (in some measure) connected in 8 corners and rotatable around these corners. As a whole it looks like the parallel projection of a spatial cuboid but is meant as a planar device. If fixed in one of the corner points, say, it possesses two degrees of freedom which allow complicated motions. If fixed in two opposite corner points which we call and its motion is restricted by one degree of freedom to two circles and the motion of one of the free corner points called forces to move the other free corner points in correlated way and the whole motion goes along two circles with radius equal to 1 around the two fixed points and due to equal lengths of the arms. In a minimum variant of the rhombic bicom- passes which is sufficient for our purposes we may omit 7 arms, for example, and get the device shown on the right-hand side in Figure 2. All this means that the rhombic bicompasses are more than only connected double compasses².

As coordinate origin we choose the point which possesses then the plane coordinates. The co- ordinates of the second fixed point we denote by. We parameterized the rotation of the point of the rhombic bicompasses by the rotation angle and calculated the motion of all other points in de- pendence on this parametrization. The results of these calculations are presented in Appendix A. For the special purpose of the construction of the regular heptagon the second fixed point of the rhombic

bicompasses has to be specialized as the point with Cartesian coordinates with the

distance from to equal to which can be constructed by compasses and ruler. Since we have

the root sum for the roots which are somewhere on the circle around the

coordinate origin its sum ends on the fixed point. This guarantees that in a certain position of the rhombic bicompasses which up to now we do not know the points correspond exactly to the roots. Since the point lies on the bisection of the angle between and. Thus we have now to find the position of the rhombic bicompasses where the point lies on the bisection of the angle between points and. This can be made by a simple additional device with two arms of equal but arbitrary (within certain limits) lengths and rotatable around movable point which we connect rotatably with the points and (see Figures 3-5). When the point reaches the prolongation of the line from to it bisects the angle from coordinate origin between and and the corresponding point

of the rhombic bicompasses possesses then the desired coordinates and the point the coordinates, respectively, and the essential part of the problem of the construction of

the regular heptagon is completed (Figure 5). Since the same construction as here described with the points leading to the roots can be also made with the points leading to the roots (see Figure 5 on right-hand side).

Apart from the rhombic bicompasses as a new mean for geometrical constructions it is necessary to refer to a further difference to usual constructions by compasses and ruler. The bisection of an angle cannot be made in our construction at a final stage of a figure but has to be controlled continuously in the process of construction by the rhombic bicompasses.

4. Alternative Method to the Described Angle Bisections

From Figure 1 it is seen that the prolonged ray from coordinate origin through the point which lies on the unit circle around of the complex plane goes also through the point which lies on the unit circle around the point. This becomes clear from the fraction

(8)

which is a real number. From Figure 1 it is also seen that the line between the points and goes through the point (denoted by) of the complex plane. This line is described in parametric re- presentation with the parameter by

(9)

It is easy to check that for parameter value according to

(10)

the line (9) goes exactly through the point of the complex plane (point in Figure 4 and Figure 5). This can also be used for the determination of the right position of the rhombic bicompasses for the construction of the regular heptagon by controlling the angle for which the line between points and goes through the point. Using this the absolute minimum bicompasses in Figure 3 are already sufficient for

the construction of the angle which is then the angle between the sides and from coordinate

origin (see also Figure 5 and Figure 1).

5. A few Words about Neusis Construction of the Regular Heptagon

The known construction of the regular heptagon rests on the trisection of an arbitrary angle attributed to Archimedes and belongs to a kind of constructions which is often called a neusis construction [3] [8] (see there also for word explanation from the Greek). It is not possible by compasses and unmarked ruler where the ruler serves to draw a line between given points but neusis constructions require to fit a given length markable on a ruler in such a way that it intersects at once a given line and a given circle or second line with its marked ends and where the ruler has to go through a further given point on the circle which cannot be fixed on the ruler and has to be fitted (e.g., [1] - [3] [7] [8] ).

The equation for the trisection of a given angle and therefore of its given is

(11)

The cubic Equation (1) for leads with a substitution to the same type of Equation (11) with 3 real solutions, concretely to

(12)

which is equivalent to a certain Cosine of an angle according to or and

thus which can be constructed by compasses and ruler. The trisection of this angle

(corresponds approximately to) is then to make by the neusis construction of Archimedes and from the positive solution one can determine then according to (the two negative solutions for correspond to and to)

(13)

which is possible by compasses and ruler. Detailed such neusis constructions can be found in the given references [3] [8] , in [3] in addition to case also constructions for.

6. Conclusion (with a Short Outlook on 7-Fold Symmetry in Living Nature)

It was shown that the regular heptagon can be constructed by a new mean which we called rhombic bicompasses in connection with a ruler. The rhombic bicompasses allow to draw at once two circles of given fixed distance of their centers in such correlated way that the position of one arm determines the positions of all other arms. Evidently, the solution of a cubic equation which is necessary for the construction of the regular heptagon is hidden in the correlation of the arms of the bicompasses and, explicitly, appear only square roots in the points for the construction, for example, the distances of the fixed points of the rhombic bicompasses.

One may ask whether or not it is possible to construct other regular -gons for prime numbers by rhombic bicompasses. The case is the worst case up to since the palindromic polynomial to the cyclotomic equation for can only be factorized into the product of two polynomials of 5-th degree with

coefficients which contain only square radicals and with the roots corresponding to

in one and in the other polynomial that leads to 5-th degree equations of general form which cannot be solved in radicals due to absent further symmetries of the roots in each cycle [2] [4] [10] . This is as it is known not possible to construct by compasses and ruler and also not by the new mean of rhombic bicompasses. The palindromic part of the cyclotomic equation for after separation of factor can be factorized into 4 polynomials of third degree with only (complex) quadratic radicals in the coefficients but corresponding to two different sums of three roots and therefore apart from coordinate origin

to two different centers of the bicompasses which are and, correspondingly (or of their complex conjugate), and with the roots corresponding to and (or to their complex conjugate

and) in each polynomial factor of third order. This means that one does not have angles and doubled angles in one cycle but, at least, only angles and their threefold angles such as in and the construction by the bicompasses is only possible in connection with a neusis construction to fix the trisection of an angle during the correlation of the points on one circle. Since, however, this neusis construction can be made only during the controlled work with the bicompasses it cannot be considered as an appropriate geometric construction. The case of the regular polygon to is well known as constructible by compasses and ruler since the 16-th order palindromic part of the cyclotomic equation can be resolved by products of second-degree equations with only quadratic radicals in the coefficients. As is very famous, Gauss discovered this in 1796 (published in “Disquisitiones Arithmeticae” in 1801) and he found

additionally that all regular polygons with odd of the form to non-negative

integers if resulting are prime numbers (Fermat numbers) and therefore, clearly, with all even by angle bisections are constructible by compasses and ruler [1] -[9] .

Let us make some remarks on seven-fold symmetries in living things. Nature does not often realize the symmetry of a regular heptagon contrary to ubiquitous cyclic symmetries and and more rarely also (e.g., Dryas octopetala, Rosaceae (mountain avens)) and nearly in the flowers of flowering plants. Mostly this is combined with mirror symmetry in form of instead of alone but certain exception are species of Apocynaceae, the dogbane family, e.g., Nerius oleander (oleander), Vinca minor (lesser periwinkle) and Plumeria (frangipani) which possess only but not. One may ask why this is so and does it possess somewhat of a far connection to impossible constructibility by compasses and ruler. In other words: is it more difficult for nature to realize 7-fold symmetry than 3-, 4-, 5- or 6-fold symmetry. One example from nature for a 7-fold symmetry is the flower of Trientalis europaea, Primulaceae (chickweed wintergreen; in German: Europäischer Siebenstern, substituted by Trientalis borealis, T. latifolia in North America) that, however, is even an exception among the Primula family which members mostly possess a stable 5-fold symmetry. This 7-fold symmetry of Trientalis europaea is not very stable since one may often find exemplars of this species with 6-fold symmetry and more rarely with 8-fold symmetry as one can see from pictures and as I found by myself in nature. A 7-fold symmetry is very rare within the world of living organisms also in the other kingdoms such as animals (e.g., a few species of sea stars with seven arms), whereas astonishingly the 5-fold symmetry is very common in the kingdom of plants, in particular, within the flowering plants in Dicotyledones (e.g., the most species of the families Rosaceae, Primulaceae, Boraginaceae, Solanaceae, Saxi- fragaceae, Campanulaceae, Geraniaceae, Malvaceae, Linaceae among others and some families with a major part of species with -fold symmetry such as Ranunculaceae, Caryophyllaceae, Ericaceae and Gentianaceae, in these cases also species with -fold symmetry and zygomorphic species in the first). Clearly, there are also families with only 4-fold symmetry of the flowers (e.g., Rubiaceae and Brassicaceae, in last case only the petals and sepals but not the 6 stamens) and also -, and -fold symmetries and (most Mono- cotyledones) mostly combined with mirror symmetries in form of.

Acknowledgements

We note here commendably that all figures are made using Wolfram’s “Mathematica 6”.

Cite this paper

A.Wünsche, (2014) Construction of Regular Heptagon by Rhombic Bicompasses and Ruler. Applied Mathematics,05,2370-2380. doi: 10.4236/am.2014.515229

References

Appendix A. Points and Geometric Objects in the Rhombic Bicompasses Fixed at Points and

We collect here the results of Cartesian coordinates corresponding to the complex number for the positions of the points of rhombic bicompasses with two opposite points fixed at the coordinate origin and at a general point which we later specialize for the regular heptagon

(1)

The movable points of rhombic bicompasses on the circle around in dependence on the angle possess the coordinates (see Figure 2)

(2)

and on the circle around

(3)

with the abbreviation

(4)

where changing the sign of the root interchanges the points and. Using the given coordinates one may easily check the independence of the following distances on the angle

(5)

The above formulae are necessary to reproduce the given figures for the bicompasses and for the construction of the regular heptagon.

In case of the regular heptagon, we have to apply (2) and (3) in connection with (4) in the specialization

(6)

In particular, for from which follows the bicompasses take on a special degenerate

position with identities, , and and forming

two bordering rhombi of equal form.

The points and for angle bisections are parameterized by the angle and the arbitrary parameters

and (within certain limits) using by

(7)

with the distances

(8)

If we set in the above formula we obtain for points on the regular heptagon corresponding

to the roots of the cyclotomic equation for and for a point on the half angle between the roots and.

NOTES

¹In addition, we note that when trying to solve the equation by “Mathematica 6”, it provides the roots only in the form equiva- lent to.

²It is easy to build a primitive model of rhombic bicompasses by simple means such as the arms from thin cardboard and with rivets at the corners to allow rotations.