Applied Mathematics
Vol.5 No.4(2014), Article ID:43843,12 pages DOI:10.4236/am.2014.54073
Nelson-Aalen and Kaplan-Meier Estimators in Competing Risks
Didier Alain Njamen-Njomen1,2, Joseph Ngatchou-Wandji3
1Department of Mathematics and Computer Sciences, Faculty of Sciences, University of Maroua, Maroua, Cameroon
2Department of Mathematics, Faculty of Sciences, University of Yaounde 1, Yaounde, Cameroon
3University of Lorraine, Lorraine, France
Email: dangaza@yahoo.fr, didiernjamen1@gmail.com, Joseph.ngatchou-wandji@univ-lorraine.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 11 December 2013; revised 11 January 2014; accepted 18 January 2014
ABSTRACT
In this paper, stochastic processes developed by Aalen [1] [2] are adapted to the Nelson-Aalen and Kaplan-Meier [3] estimators in a context of competing risks. We focus only on the probability distributions of complete downtime individuals whose causes are known and which bring us to consider a partition of individuals into sub-groups for each cause. We then study the asymptotic properties of nonparametric estimators obtained.
Keywords:Censored Data; Counting Process; Competitive Risk; Non-Parametric Estimators; The Cumulative Incidence Function; Risk Function Specific Cause; Conditional Distribution Function

1. Introduction
Let us consider a data model which lives time where the event of interest is a failure (or death) due to the 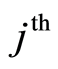 event,
event, 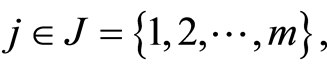 and the non-zero integer m, the number of possible causes. By convention,
and the non-zero integer m, the number of possible causes. By convention,  corresponds to the state of functioning (or of life) of the observed individual. It is assumed that the observation is stopped when a failure (or death) occurs, but this observation may be right-censored in a non-informative way. Some examples of this situation corresponds to the case where the event of interest is due to another cause, or withdrawal of the individual from the study or at the end of the study. In the case of right censoring time, the time of failure of year for individuals and their causes are not known to the experimenter. A data model as described above is commonly called “competing risks model” (or competitors) and is studied in fields such as medical control, demography, actuarial science, economics or industrial reliability. In Andersen et al. [4] , an illustration and details of mathematics techniques on competing risks in biomedical applications are developed. For example in the study of AIDS, the different competitive risks can be 1) death due to AIDS, 2) death due to tuberculosis or 3) death due to other causes and in this case
corresponds to the state of functioning (or of life) of the observed individual. It is assumed that the observation is stopped when a failure (or death) occurs, but this observation may be right-censored in a non-informative way. Some examples of this situation corresponds to the case where the event of interest is due to another cause, or withdrawal of the individual from the study or at the end of the study. In the case of right censoring time, the time of failure of year for individuals and their causes are not known to the experimenter. A data model as described above is commonly called “competing risks model” (or competitors) and is studied in fields such as medical control, demography, actuarial science, economics or industrial reliability. In Andersen et al. [4] , an illustration and details of mathematics techniques on competing risks in biomedical applications are developed. For example in the study of AIDS, the different competitive risks can be 1) death due to AIDS, 2) death due to tuberculosis or 3) death due to other causes and in this case  (see Figure 1).
(see Figure 1).
It is important to note that in most data models in competing risks, the functions that characterize the probability distribution of the variable of interest and the marginal are not always observable (see Tsiatis [5] , Heckman and Honoré [6] ). Issues to be resolved include virtually the underlying functions for different causes and effects of covariates on the rate of occurrence of competing risks. One of the problems we may face is that the information on the cause of failure of the individual observation can only be known after the autopsy, while we don’t know anything about individuals censored in monitoring. In addition, the incident distributions (due to specific causes) do not allow to describe satisfactorily the probabilities of the various marginal (failures  case
case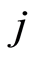 ) in competing risks models. Assumptions of independence of competing risks can help ensure observability in some cases, but they are not reasonable only in such models.
) in competing risks models. Assumptions of independence of competing risks can help ensure observability in some cases, but they are not reasonable only in such models.
1.1. Related Works
The estimators of Nelson-Aalen and Kaplan-Meier [3] are generally studied in the literature following two approaches: firstly, the method of martingale (Aalen [1] [2] ; Andersen et al. [4] ; Fleming and Harrington [7] , Prentice et al. [8] ) and secondly the law of the iterated logarithm (Breslow and Crowley [9] , Földes and Rejtö [10] or Major and Rejtö [11] , Földes and Rejtö [12] , Gill [13] , Csörgö and Horváth [14] , Ying [15] and Chen and Lo [16] ). Recently, applications have been made in the context of competing risks (Latouche [17] ; Belot [18] ). Latouche [17] states that during the planification of clinical trials, the evaluation of the number of patients to be included is a critical issue because such a formulation does not exist in the Fine and Gray’s [19] model. For this purpose, he therefore computes the number of patients within the context of competition for an inference based function on cumulative incidence and then, he studies the properties of the model of Fine and Gray when it is wrongly specified. Belot [18] presents the data got from randomized clinical tests on prostate cancer patients who died for several reasons.
1.2. Contributions
In this paper, the stochastic processes developed by Aalen [1] [2] are adapted to Nelson-Aalen and KaplanMeier estimators [3] in a context of competing risks (e.g. Aalen and Johansen [20] , Andersen et al. [4] ). We focus only on the complete probability distributions of downtime individuals whose causes are known and which bring us to consider a partition of individuals sub-groups for each cause. We provide a new proof of the consistency of the Nelson-Aalen estimator in the context of competing risks by using the method of martingale. Under the regularity assumptions for the sequence 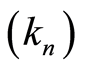 (
(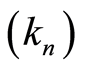 is a sequence of integers such that
is a sequence of integers such that 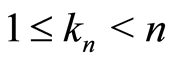 and
and  is the number of observable samples) we obtain an almost-safe speed estimator of Kaplan-Meier [3] which is the same as that obtained by Giné and Guillou [21] which is
is the number of observable samples) we obtain an almost-safe speed estimator of Kaplan-Meier [3] which is the same as that obtained by Giné and Guillou [21] which is 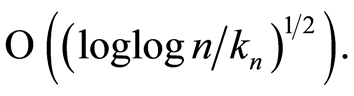
The rest of the paper is organized as follows: Section 2 describes preliminary results and notations used in the paper and Section 3 evaluates the conditional functions of distribution to the specific causes. Section 4 contains the main results of the paper as well as some properties of our estimators obtained. The last section concludes the paper.
2. Preliminary Results
Lifetime analysis (also referred to as survival analysis) is the area of statistics that focuses on analyzing the time

Figure 1. Example of 3 risks competing model.
duration between a given starting point and a specific event. This endpoint is often called failure and the corresponding length of time is called the failure time or survival time or lifetime.
Formally, a failure time is a nonnegative random variable (r.v.) 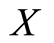 that describes the length of time from a time origin until an event of interest occurs. We will suppose throughout that
that describes the length of time from a time origin until an event of interest occurs. We will suppose throughout that 
The most basic quantities used to summarize and describe the time elapsed from a starting point until the occurrence of an event of interest are the distribution function and the hazard function. The cumulative distribution function at time  also called lifetime distribution or the failure distribution, is the probability that the failure time of an individual is less or equal than the value
also called lifetime distribution or the failure distribution, is the probability that the failure time of an individual is less or equal than the value 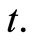 It is given for
It is given for 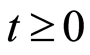 by:
by: 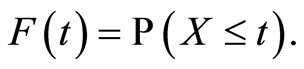
The function  is right-continuous, nondecreasing and satisfies
is right-continuous, nondecreasing and satisfies  and
and 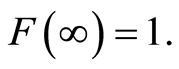 We denote by
We denote by 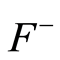 the left-continuous function obtained from
the left-continuous function obtained from 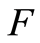 in the following way:
in the following way:
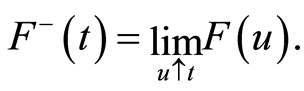
The distribution of  may equivalently be dealt with in terms of the survival function which is given, for
may equivalently be dealt with in terms of the survival function which is given, for 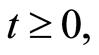 by:
by:
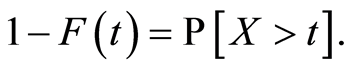
The cumulative hazard function is defined for  by:
by:
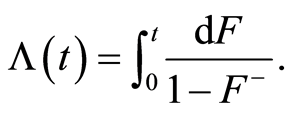
When 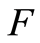 is continuous, the relation
is continuous, the relation  is valid for all
is valid for all  We can then call
We can then call 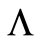 the log-survival function.
the log-survival function.
If 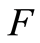 admits a derivative with respect to Lebesgue measure on
admits a derivative with respect to Lebesgue measure on  the probability density function exists and is defined for
the probability density function exists and is defined for 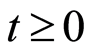 by:
by:
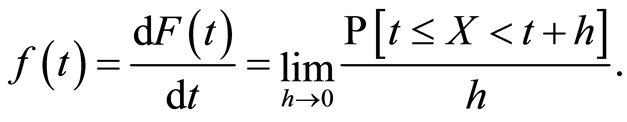
Heuristically, the function  may be seen as the instantaneous probability of experiencing the event.
may be seen as the instantaneous probability of experiencing the event.
With the same hypothesis of differentiability, the hazard function exists and is defined for  by:
by:
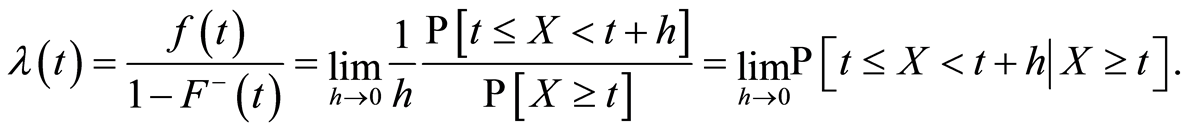
The quantity  can be interpreted as the instantaneous probability that an individual dies at time
can be interpreted as the instantaneous probability that an individual dies at time  conditionally on he or she having survived until that time.
conditionally on he or she having survived until that time.
For an extensive introduction to lifetime analysis, the reader is referred e.g. to the books of Cox and Oakes [22] and Kalbfleisch and Prentice [23] .
The main difficulty in the analysis of lifetime data lies in the fact that the actual failure times of some individuals may not be observed. An observation is right-censored if it is known to be greater than a certain value, provided the exact time is unknown. Let  be the nonnegative r.v. with distribution function
be the nonnegative r.v. with distribution function 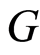 that stands for the censoring time of the individual. As before, the nonnegative r.v.
that stands for the censoring time of the individual. As before, the nonnegative r.v. 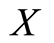 with distribution function
with distribution function 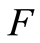 denotes the failure time of the individual. If
denotes the failure time of the individual. If 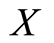 is censored, instead of
is censored, instead of 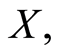 we observe
we observe  which gives the information that
which gives the information that 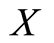 is greater than
is greater than 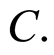 In any case, the observable r.v. consists of
In any case, the observable r.v. consists of 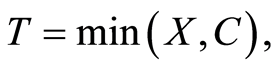
 , where
, where  denotes the indicator function. The nonnegative r.v.
denotes the indicator function. The nonnegative r.v.  stands for the observed duration of time which may correspond either to the event of interest
stands for the observed duration of time which may correspond either to the event of interest 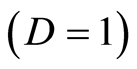 or to a censoring time
or to a censoring time 
As a sequel to above, it is assumed that 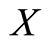 and
and 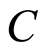 are independent. Consequently, the random variable
are independent. Consequently, the random variable 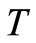 has the distribution function
has the distribution function 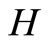 given by
given by
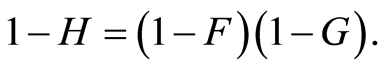
The following subdistribution functions of 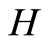 will be needed:
will be needed:
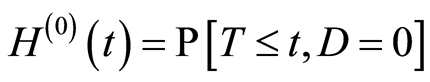
and
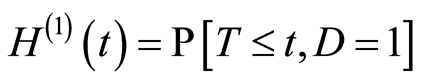
The relation
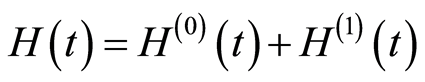
is valid for any 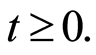
The relations that connect the subdistribution functions 
 and to the distribution functions
and to the distribution functions 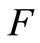 and
and 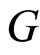 are given by:
are given by:

and
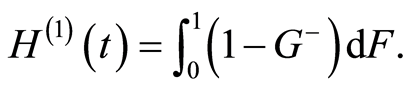
The cumulative hazard function of  can be expressed as:
can be expressed as:
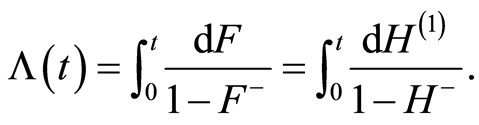
Kaplan and Meier [3] introduced the product-limit estimator for the survival distribution function. The estimator of the cumulative hazard function is the Nelson-Aalen estimator introduced by Nelson [24] [25] and generalized by Aalen [1] [2] .
Let  for
for 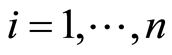 be
be  independent copies of the random vector
independent copies of the random vector  Let
Let 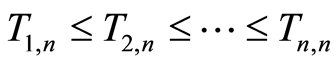 be the order statistics associated to the sample
be the order statistics associated to the sample  If there are ties between a failure time (or several failure times) and a censoring time, then the failure time(s) is (are) ranked ahead of the censoring time(s).
If there are ties between a failure time (or several failure times) and a censoring time, then the failure time(s) is (are) ranked ahead of the censoring time(s).
We define the empirical counterparts of 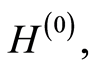
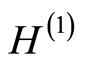 and
and 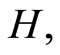 by:
by:



The Kaplan-Meier product-limit estimator is defined for 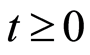 by:
by:

The Nelson-Aalen estimator for  is then defined for
is then defined for 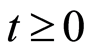 by:
by:

The following relations are valid for 

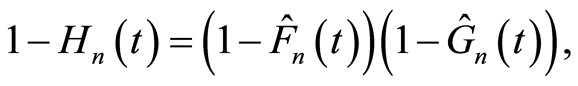

where  the Kaplan-Meier estimator of
the Kaplan-Meier estimator of , is defined for
, is defined for 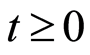 by:
by:

Let 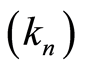 be a sequence of integers between
be a sequence of integers between  and
and 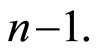 In order to always have asymptotical results, we suppose that the sequence
In order to always have asymptotical results, we suppose that the sequence 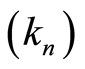 satisfies the following hypothesis:
satisfies the following hypothesis:
 for
for 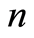 large enough, the sequence
large enough, the sequence 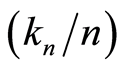 is non-increasing and
is non-increasing and 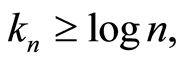
 for
for 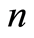 large enough, the sequence
large enough, the sequence 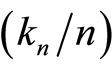 is non-increasing and there exists a constant
is non-increasing and there exists a constant  such that
such that  with
with 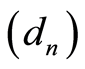 is a non-increasing sequence such that:
is a non-increasing sequence such that:
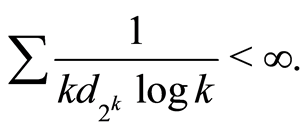
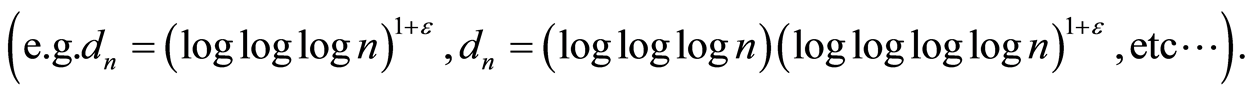
Condition 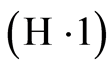 is required when applying the results of Gin? and Guillou [21] while Condition
is required when applying the results of Gin? and Guillou [21] while Condition  is required when applying the results of Cs
is required when applying the results of Cs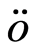 rgö [26] .
rgö [26] .
The following result formulates the laws of the iterated logarithm-type (LIL-type) result on the mentioned increasing intervals.
Theorem 1 (Csörgö [26] ; Giné and Guillou [21] ) Let 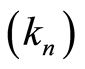 be a sequence of integers such that
be a sequence of integers such that 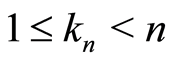 and, for the almost sure results, satisfying
and, for the almost sure results, satisfying  We have1:
We have1:
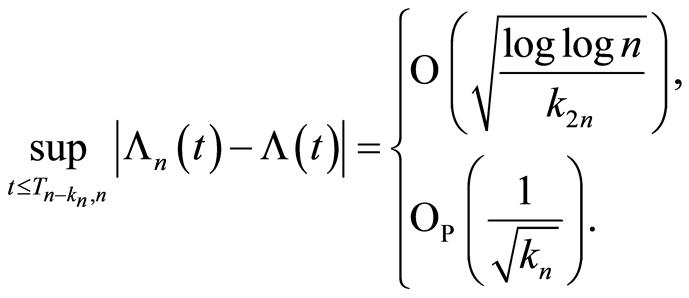
If, in addition, 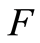 is assumed continuous, then we also have:
is assumed continuous, then we also have:

Proof. See Csörgö [26] ; Giné and Guillou [21] . 
The continuity of 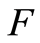 is required to linearize the Kaplan-Meier process. Indeed, if
is required to linearize the Kaplan-Meier process. Indeed, if 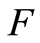 is continuous, then
is continuous, then 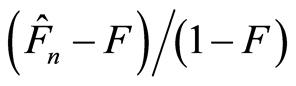 can be approximated by
can be approximated by 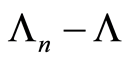 on the random interval
on the random interval 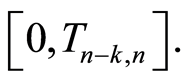 Precisely, we have the following result.
Precisely, we have the following result.
Proposition 1 (Giné and Guillou [21] ) Let 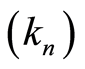 be a sequence of integers satisfying
be a sequence of integers satisfying 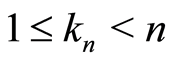 and Hypothesis
and Hypothesis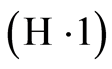 . If
. If 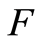 is continuous, then
is continuous, then
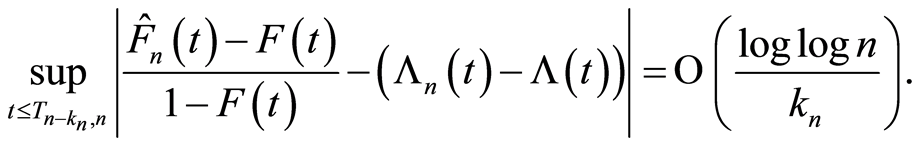
Proof. See Giné and Guillou [21] . 
3. Evaluation of the Conditional Functions of Distribution to the Specific Causes
Let 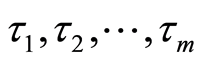 be a continuous random variables representing respectively the lifetimes in each of the
be a continuous random variables representing respectively the lifetimes in each of the  risks competing,
risks competing,  be the set of index cause, where 0 corresponds to the condition of the individual observed,
be the set of index cause, where 0 corresponds to the condition of the individual observed, 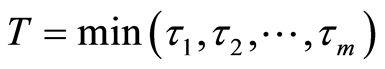 the random variable of the event of interest and
the random variable of the event of interest and 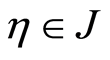 the random variable case, where
the random variable case, where 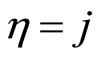 if
if 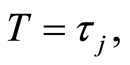 for all
for all 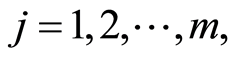
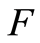 is the distribution function of
is the distribution function of 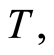
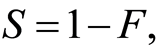 the survival function such that
the survival function such that  the random variable C of the event censoring right,
the random variable C of the event censoring right,  and for technical reasons,
and for technical reasons, 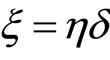 such that
such that  if (
if (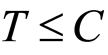 and
and ) and
) and 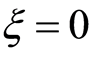 if
if .
.
We notice that 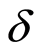 and
and 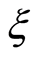 are observable and
are observable and 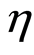 is so only for
is so only for 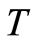 uncensored.
uncensored.
We assume that censorship is not informative. The joint law 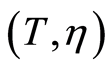 is completely specified by the specific incident distributions cause
is completely specified by the specific incident distributions cause 
 defined by
defined by
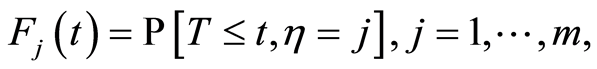 (1)
(1)
which are none other than the sub-distributions of the specific cause of failure 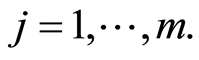
The cumulative hazard rate of specific-cause  corresponding to
corresponding to 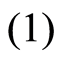 is given by
is given by
 (2)
(2)
Let 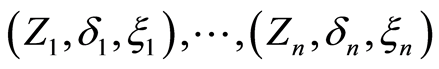 be n-sample of observable triplet
be n-sample of observable triplet 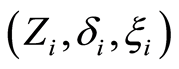 where
where 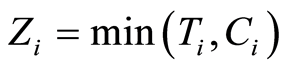 and
and  , with
, with 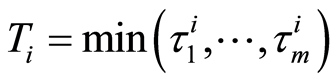 and where
and where 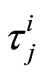 represent the time that an individual
represent the time that an individual 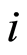 is subject to the cause
is subject to the cause  If
If 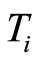 and
and  are independent, the random variable
are independent, the random variable 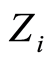 admits distribution function
admits distribution function 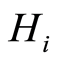 defined by
defined by 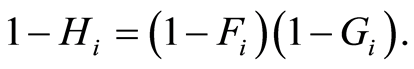 Then the Nelson-Aalen estimator of
Then the Nelson-Aalen estimator of 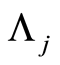 is given for
is given for 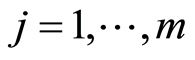 by (see e.g. in Andersen et al. [4] )
by (see e.g. in Andersen et al. [4] )
 (3)
(3)
with

and where
 (4)
(4)
is the counting of the number of failures observed in case of 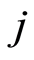 the time interval
the time interval 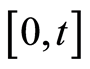 and
and
 (5)
(5)
is the number of individuals in the sample observation that survive beyond time 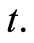 Thus, for any
Thus, for any 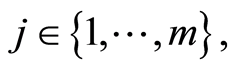
 (6)
(6)
represents the number of individuals who may fall down specific cause 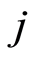 or be censored.
or be censored.
Estimator similar  analogue to (2) and on the sub-group
analogue to (2) and on the sub-group  individuals crashing case
individuals crashing case 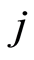 is given by
is given by
 (7)
(7)
and with  and
and

The relation between the cumulative hazard rate 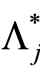 and survival
and survival  in the subgroup Aj is given by2
in the subgroup Aj is given by2
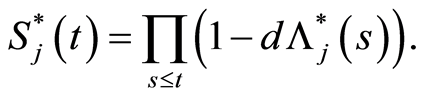 (8)
(8)
A nonparametric estimator of the distribution function  of time life in subgroups
of time life in subgroups 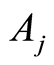 is defined by
is defined by
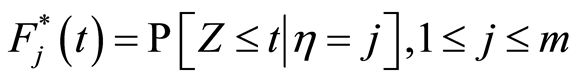 (9)
(9)
is given by
 (10)
(10)
The size  of the subgroup
of the subgroup 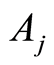 individuals is not observable due to the inaccessibility of all subgroups of specific causes
individuals is not observable due to the inaccessibility of all subgroups of specific causes 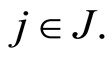 Nevertheless, we can assign a probability
Nevertheless, we can assign a probability  to each of the individuals belonging to one of the
to each of the individuals belonging to one of the 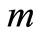 subgroups. Thus, one can estimate the size
subgroups. Thus, one can estimate the size 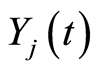 by
by 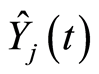 given by ( see e.g. in Satten and Datta [27] or Datta and Satten [28] )
given by ( see e.g. in Satten and Datta [27] or Datta and Satten [28] ) 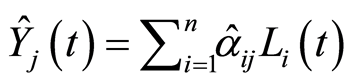 where
where  is the estimator of the probability that the individual n˚
is the estimator of the probability that the individual n˚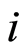 in the sample subgroup
in the sample subgroup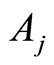 , subset of risk of specific-cause
, subset of risk of specific-cause . Thus, the final estimators for the cumulative hazard rate
. Thus, the final estimators for the cumulative hazard rate 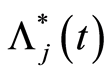 due to the specific cause
due to the specific cause 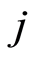 and the corresponding distribution function
and the corresponding distribution function  have the respective expressions
have the respective expressions
 (11)
(11)
and for 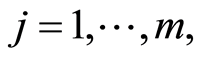
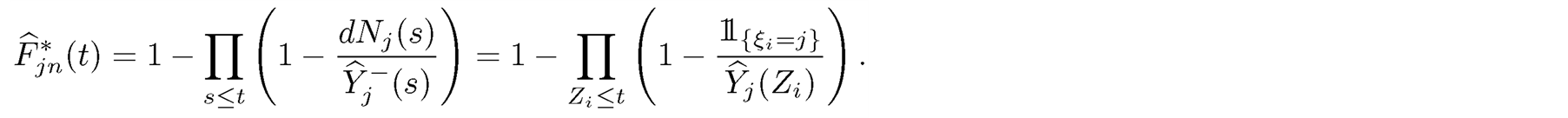 (12)
(12)
4. Main Results
Let  be a positive random variable and
be a positive random variable and 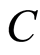 be a censoring variable such that
be a censoring variable such that  and
and  In this model of random censorship, for a sample
In this model of random censorship, for a sample 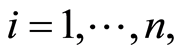 subject to a specific causes
subject to a specific causes  we can observe the couple
we can observe the couple 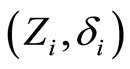 where
where 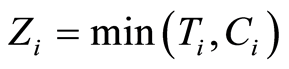 and
and  with
with  and where
and where 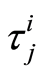 is the time that an individual
is the time that an individual  is subject to the cause
is subject to the cause 
For a given  and an individual
and an individual 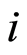 with
with  the counting process is defined by:
the counting process is defined by:

Therefore, if an individual 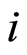 undergoes event before time
undergoes event before time 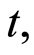 then
then 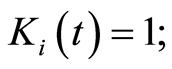 otherwise
otherwise 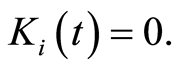 We can also define the counting process
We can also define the counting process

Naturally, it appears that we considered the information provided over time as a filter, which is used to describe the fact that past information is contained in the current information, hence we have the natural filtration 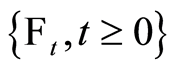 where
where
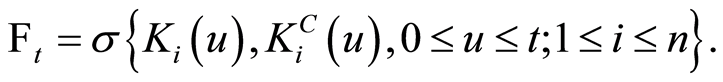
For 
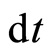 and for
and for  we have
we have
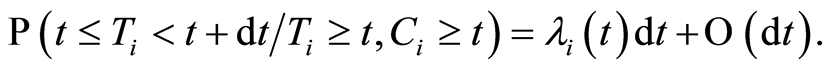
If 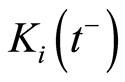 denotes the left boundary at
denotes the left boundary at 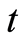 of
of 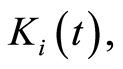 we have
we have
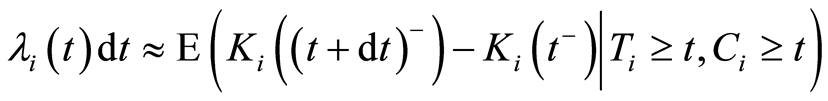
since, the quantity  takes only the values 0 and 1.
takes only the values 0 and 1.
For a given 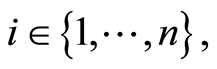 we define the function
we define the function

which indicates whether the individual 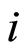 is still at risk just before time
is still at risk just before time  (the individual has not yet undergone the event). Therefore• if
(the individual has not yet undergone the event). Therefore• if  then,
then,  and
and
• if 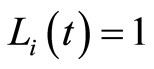 then,
then,

where 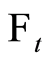 is the natural filtration (all information available at time
is the natural filtration (all information available at time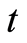 ), where the notation
), where the notation  refers to formal writing of the stochastic integral
refers to formal writing of the stochastic integral
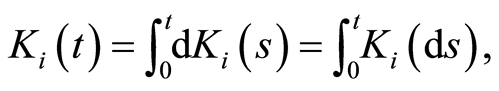
writing made possible because 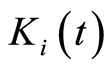 is a growing process. The expression of
is a growing process. The expression of  in function of the counting process
in function of the counting process  is given by
is given by
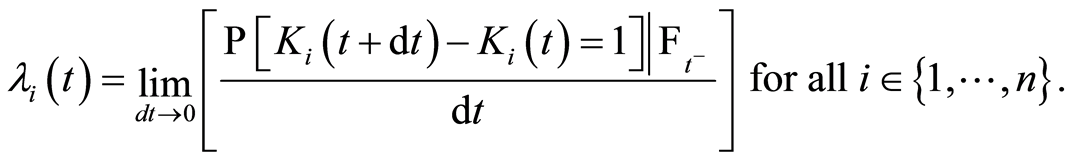
Thus, we have 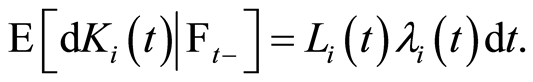
The stochastic process defined for 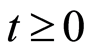 and
and 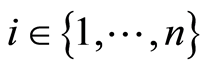 by
by
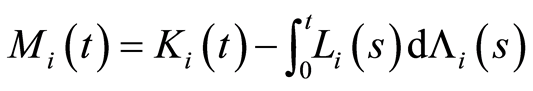
is the martingale associated with the subject at risk  Thereafter
Thereafter  is the compensating process
is the compensating process 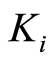 because it is the integral of the product of two predictable processes.
because it is the integral of the product of two predictable processes.
Theorem 2 Let 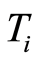 be an absolutely continuous lifetime and
be an absolutely continuous lifetime and 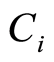 be a censoring variable for any arbitrary distribution
be a censoring variable for any arbitrary distribution 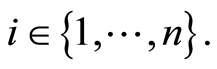 Let
Let 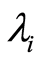 be the risk function associated with
be the risk function associated with  Let’s put
Let’s put 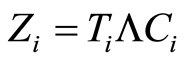 and
and  .
.
For 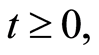 the process defined by
the process defined by

is a 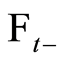 martingale if and only if
martingale if and only if
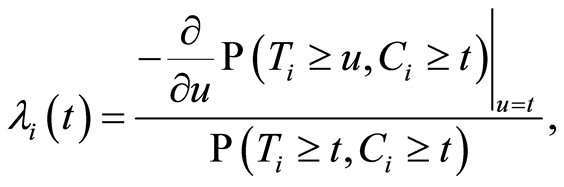
for 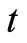 such that
such that 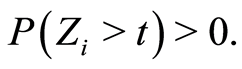
Proof. See Breuils ([30] , p. 25) and Fleming and Harrington ([7] , p. 26). 
For a given 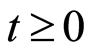 and a given
and a given , the expressions of
, the expressions of ,
, 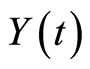 and
and  are those of formulas (4), (5) and (2) respectively. Using these notations, we can directly obtain the following preliminary result:
are those of formulas (4), (5) and (2) respectively. Using these notations, we can directly obtain the following preliminary result:
Proposition 2 For a given  and a given
and a given , the stochastic processes defined by
, the stochastic processes defined by
 (13)
(13)
is the martingale associated with the subject specific cause 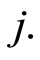
Proof.

The martingale 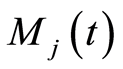 represents the difference between the number of failures due to a specific cause
represents the difference between the number of failures due to a specific cause 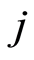 observed in the time interval
observed in the time interval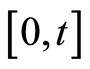 , i.e.
, i.e.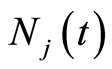 , and the number of failures predicted by the model for the
, and the number of failures predicted by the model for the  cause. This definition fulfills the Doob-Meyer decomposition.
cause. This definition fulfills the Doob-Meyer decomposition.
The first result of this paper concerns the consistency of the Nelson-Aalen estimator for the competing risks based on martingale approach.
Theorem 3 For 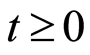 such that
such that  we have
we have
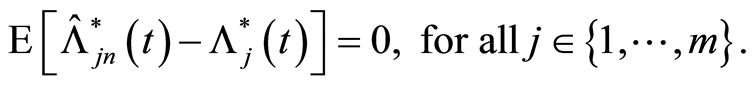
Proof.
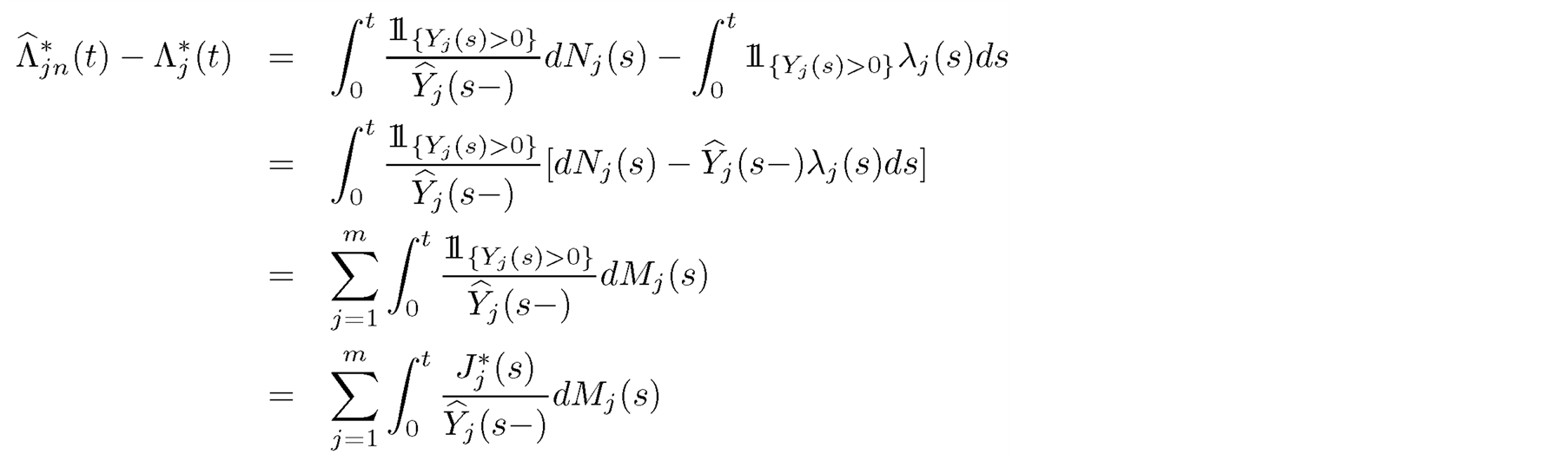
where the expectation of the martingale  (specific for
(specific for  cause) is equal to zero and where
cause) is equal to zero and where 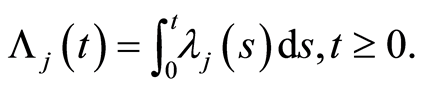 Indeed,
Indeed,
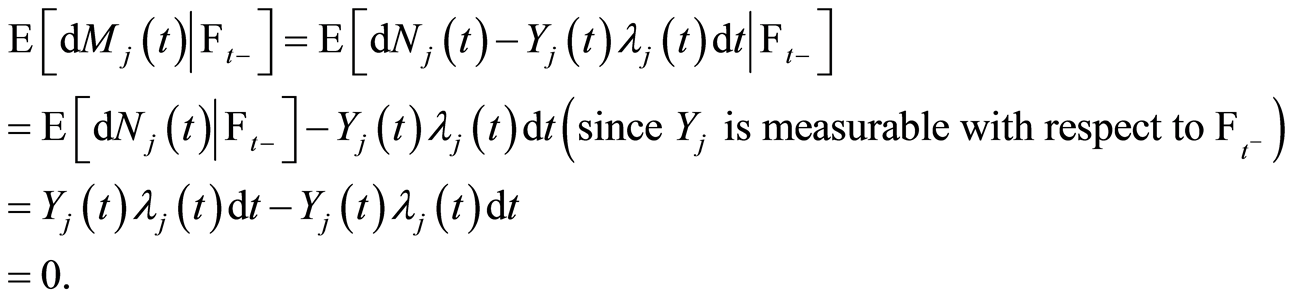
Hence, we arrive at result.
Using the fact that

we have:
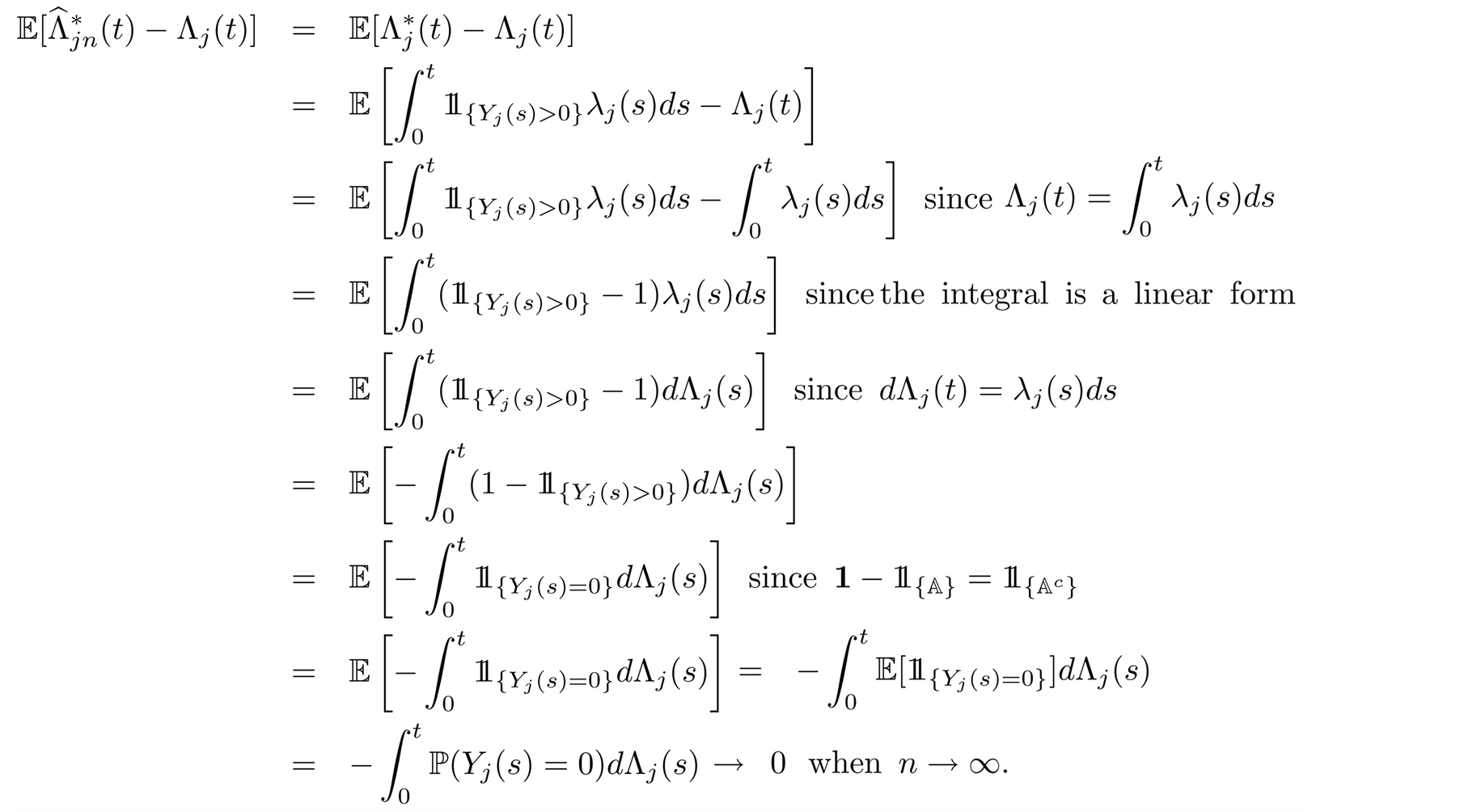
It follows that 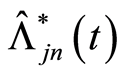 is an asymptotically unbiased estimator of
is an asymptotically unbiased estimator of 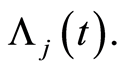 Hence, we arrived at result.
Hence, we arrived at result. 
Our second LIL-type result provides almost sure and in probability rates of convergence of  to
to 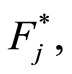 for
for 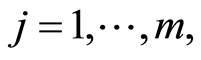 uniformly over the random increasing intervals
uniformly over the random increasing intervals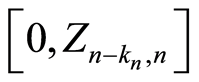 . (See is Deheuvels and Einmahl [31] [32] for very fine results of the model law iterated logarithm functional and available in a point or on a compact strictly included in the support of H). This result is consistent with that of Stute [33] which constitutes a compromise between the results of Breslow and Crowley [9] , Földes and Rejtö [10] or Major and Rejtö [11] , and those of Földes and Rejtö [12] , Gill [13] , Csörgö and Horváth [14] , Ying [15] and Chen and Lo [16] .
. (See is Deheuvels and Einmahl [31] [32] for very fine results of the model law iterated logarithm functional and available in a point or on a compact strictly included in the support of H). This result is consistent with that of Stute [33] which constitutes a compromise between the results of Breslow and Crowley [9] , Földes and Rejtö [10] or Major and Rejtö [11] , and those of Földes and Rejtö [12] , Gill [13] , Csörgö and Horváth [14] , Ying [15] and Chen and Lo [16] .
Following Giné and Guillou [34] , we say that a non-increasing sequence 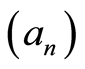 of numbers is regular if there exists a constant
of numbers is regular if there exists a constant  such that for all
such that for all 
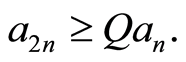 We denote by
We denote by 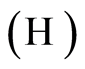 the following hypothesis:
the following hypothesis:
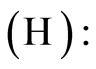 for
for 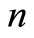 large enough, the sequence
large enough, the sequence 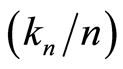 is regular non-increasing and there exists a constant
is regular non-increasing and there exists a constant 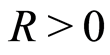 such that
such that 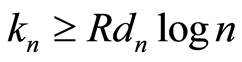 with
with 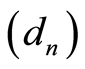 is a non-increasing sequence such that
is a non-increasing sequence such that

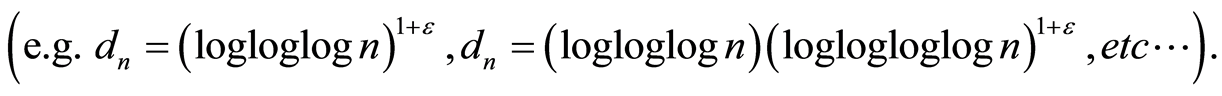
Theorem 4 Let  be a sequence of integers such that
be a sequence of integers such that  for all
for all  and which satisfies hypothesis
and which satisfies hypothesis 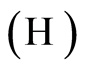 for the almost-sure part. For all
for the almost-sure part. For all 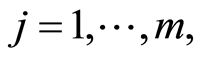 we assume that
we assume that 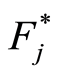 is alway continuous. Therefore,
is alway continuous. Therefore,
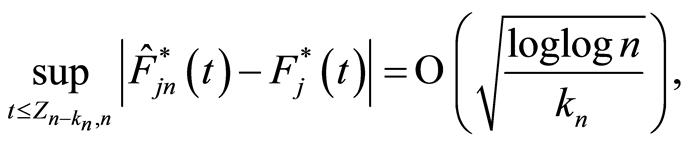
where 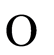 is the Landau in almost sure sense, and
is the Landau in almost sure sense, and

where 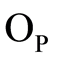 is the Landau in probability.
is the Landau in probability.
Both results of Theorem above always provides a rate in probability of uniform convergence of 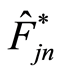 to
to  for all
for all  through a random growing intervals
through a random growing intervals 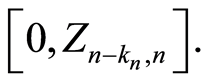
To prove Theorem 4, we have drawn from results based on the inference of empirical processes, given that in order to linearize the Kaplan-Meier process, it is necessary to impose continuity condition on 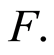 Firstly, under the Hypothesis
Firstly, under the Hypothesis 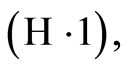 we have the following result:
we have the following result:
Lemma 1 Let 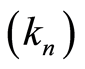 be a sequence of integers such that
be a sequence of integers such that  and, for the almost-sure results, such that
and, for the almost-sure results, such that 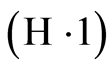 is satisfied. The rate of convergence of
is satisfied. The rate of convergence of  to
to 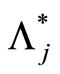 is given by
is given by

Proof. The proof of this result follows straightforwardly from the proof of the first part of Theorem 1 concerning the supremum of 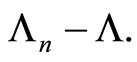
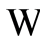
Proof of Theorem 4. The following decomposition is obtained for 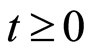 by means of integration by parts:
by means of integration by parts:
 (14)
(14)
Equality (14) entails that:

Notice that the assumption of continuity of 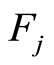 for
for 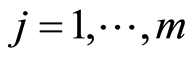 ensures that
ensures that  is continuous according to proposition 1. We then conclude with Theorem 1 and Lemma 1.
is continuous according to proposition 1. We then conclude with Theorem 1 and Lemma 1. 
5. Conclusion
In this paper, we have adapted the stochastic processes of Aalen [1] [2] to the Nelson-Aalen and Kaplan-Meier [3] estimators in a context of competing risks. We have focused particularly on the probability distributions of complete downtime individuals whose causes are known and which bring us to consider a partition of individuals into sub-groups for each cause. We have also provided some asymptotic properties of nonparametric estimators obtained.
Acknowledgements
I would like to thank Prof. Nicolas Gabriel ANDJIGA, Prof. Celestin NEMBUA CHAMENI, Prof. Eugene Kouassi for their support and their advices. I would also like to thank specially Prof. Kossi Essona GNEYOU for his collaboration and his cooperation during the preparation of this paper.
References
- Aalen, O.O. (1978) Nonparametric Estimation of Partial Transition Probabilities in Multiple Decrement Models. The Annals of Statistics, 6, 534-545. http://dx.doi.org/10.1214/aos/1176344198
- Aalen, O.O. (1978) Nonparametric Inference for a Family of Counting Processes. The Annals of Statistics, 6, 701-726. http://dx.doi.org/10.1214/aos/1176344247
- Kaplan, E.L. and Meier, P. (1958) Nonparametric Estimation from Incomplete Observations. Journal of the American Statistical Association, 53, 457-481. http://dx.doi.org/10.1080/01621459.1958.10501452
- Andersen, P.K., Borgan, Ø., Gill, R.D. and Keiding, N. (1993) Statistical Models Based on Counting Processes. Springer Series in Statistics, Spring-Verlag, New York,. http://dx.doi.org/10.1007/978-1-4612-4348-9
- Tsiatis, A. (1975) A Nonidentifiability Aspect of the Problem of Competing Risks. Proceeding of the National Academy of Sciences of the United States of America, 72, 20-22. http://dx.doi.org/10.1073/pnas.72.1.20
- Heckman, J. and Honoré, B. (1989) The Identifiability of the Competing Risks Models. Biometrika, 76, 325-330. http://dx.doi.org/10.1093/biomet/76.2.325
- Fleming, T. and Harrington, D. (1990) Counting Processes and Survival Analysis. John Wiley & Sons, Inc, Hoboken.
- Prentice, R.L., Kalbfleisch, J.D., Peterson, A.V., Flournoy, N., Farewell, V.T. and Breslow, N.E. (1978) The Analysis of Failure Times in the Presence of Competing Risks. Biometrics, 34, 541-554. http://dx.doi.org/10.2307/2530374
- Breslow, N. and Crowley, J. (1974) A Large Sample Study of the Life Table and Product-Limit Estimates under Random Censorship. The Annals of Statistics, 2, 437-453. http://dx.doi.org/10.1214/aos/1176342705
- Földes, A. and Rejtö, L. (1981) Strong Uniform Consistency for Nonparametric Survival Curve Estimators from Randomly Censored Data. The Annals of Statistics, 9, 122-129. http://dx.doi.org/10.1214/aos/1176345337
- Major, P. and Rejtö, L. (1998) Strong Embedding of the Estimator of the Distribution Function under Random Censorship. The Annals of Statistics, 16, 1113-1132. http://dx.doi.org/10.1214/aos/1176350949
- Földes, A. and Rejtö, L. (1981) A LIL-Type Result for the Product-Limit Estimator. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, 56, 75-86.
- Gill, R. (1983) Large Sample Behavior of the Product-Limit Estimator on the Whole Line. The Annals of Statistics, 11, 49-58. http://dx.doi.org/10.1214/aos/1176346055
- Csörgö, S. and Horváth, L. (1981) On the Koziol-Green Model for Random Censorship. Biometrika, 68, 391-401.
- Ying, Z. (1989) A Note on the Asymptotic Properties of the Product-Limit Estimator on the Whole Line. Statistics & Probability Letters, 7, 311-314. http://dx.doi.org/10.1016/0167-7152(89)90113-2
- Chen, K. and Lo, S.-H. (1997) On the Rate of Uniform Convergence of the Product-Limit Estimator: Strong and Weak Laws. The Annals of Statistics, 25, 1050-1087. http://dx.doi.org/10.1214/aos/1069362738
- Latouche, A. (2004) Modèles de Régression en Présence de Compétition. Thèse de Doctorat, Université de Paris, Paris.
- Belot, A. (2009) Modélisation Flexible des Données de Survie en Présence de Risques Concurrents et Apports de la Méthode du Taux en Excès. Thèse de Doctorat, Université de la Méditerranée, Marseille.
- Fine, J.P. and Gray, R.J. (1999) A Proportional Hazards Model for the Subdistribution of a Competing Risk. Journal of the American Statistical Association, 99, 496-509. http://dx.doi.org/10.1080/01621459.1999.10474144
- Aalen, O.O. and Johansen, S. (1978) An Empirical Transition Matrix for Non-Homogeneous Markov Chains Based on Censored Observations. Scandinavian Journal of Statistics, 5, 141-150.
- Giné, E. and Guillou, E. (1999) Laws of the Iterated Logarithm for Censored Data. The Annals of Probability, 27, 2042-2067. http://dx.doi.org/10.1214/aop/1022874828
- Cox, D. and Oakes, D. (1984) Analysis of Survival Data. Chapman and Hall, London.
- Kalbfleisch, J. and Prentice, R. (1980) The Statistical Analysis of Failure Time Data. John Wiley, New York.
- Nelson, W. (1969) Hazard Plotting for Incomplete Observations. Journal of Quality Technology, 1, 27-52.
- Nelson, W. (1972) A Short Life Test for Comparing a Sample with Previous Accelerated Test Results. Technometrics, 14, 175-185. http://dx.doi.org/10.1080/00401706.1972.10488894
- Csörgö, S. (1996) Universal Gaussian Approximations under Random Censorship. The Annals of Statistics, 24, 2744- 2778. http://dx.doi.org/10.1214/aos/1032181178
- Satten, G.A. and Datta, S. (1999) Kaplan-Meier Representation of Competing Risk Estimates. Statistics & Probability Letters, 42, 299-304. http://dx.doi.org/10.1016/S0167-7152(98)00220-X
- Datta, S. and Satten, G.A. (2000) Estimating Future Stage Entry and Occupation Probabilities in a Multistage Model Based on Randomly Right-Censored Data. Statistics & Probability Letters, 50, 89-95. http://dx.doi.org/10.1016/S0167-7152(00)00086-9
- Gill, R. and Johansen, S. (1990) A Survey of Product-Integration with a View toward Application in Survival Analysis. The Annals of Statistics, 18, 1501-1555. http://dx.doi.org/10.1214/aos/1176347865
- Breuils, C. (2003) Analyse de Durées de Vie: Analyse Séquentielle du Modèle des Risques Proportionnels et Tests d’Homogénéité. Thèse de Doctorat, Université de Technologie de Compiègne, Compiègne.
- Deheuvels, P. and Einmahl, J. (1996) On the Strong Limiting Behavior of Local Functionals of Empirical Processes Based upon Censored Data. The Annals of Statistics, 24, 504-525. http://dx.doi.org/10.1214/aop/1042644729
- Deheuvels, P. and Einmahl, J. (2000) Functional Limit Laws for the Increments of Kaplan-Meier Product-Limit Processes and Applications. The Annals of Statistics, 28, 1301-1335. http://dx.doi.org/10.1214/aop/1019160336
- Stute, W. (1994) Strong and Weak Representations of Cumulative Hazard Function and Kaplan-Meier Estimators on Increasing Sets. Journal of Statistical Planning and Inference, 42, 315-329. http://dx.doi.org/10.1016/0378-3758(94)00032-8
NOTES

1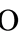 is the Landau in almost sure sense and
is the Landau in almost sure sense and 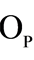 is the Landau in probability.
is the Landau in probability.

2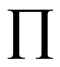 denote the product integral (see Gill & Johansen ).
denote the product integral (see Gill & Johansen ).

