Applied Mathematics
Vol.3 No.12A(2012), Article ID:26079,7 pages DOI:10.4236/am.2012.312A295
Multiple Factorial Analysis of Symbolic Data
Department de Mathematics, Faculty of Sciences, University of Yaounde 1, Yaounde, Cameroon
Email: tangahanda@yahoo.fr, aghoukeng-maths@yahoo.fr
Received September 10, 2012; revised November 13, 2012; accepted November 20, 2012
Keywords: Symbolic Object; Assertion Object; Multiple Factorial Analysis; Principle Components Analysis; Poverty
ABSTRACT
This document presents an extension of the multiple factorial analysis to symbolic data and especially to space data. The analysis makes use of the characteristic coding method to obtain active individuals and the reconstitutive coding method for additional individuals in order to conserve the variability of assertion objects. Traditional analysis methods of the main components are applied to coded objects. Certain interpretation aids are presented after the coding process. This method was applied to poverty data.
1. Introduction
Although the traditional analysis of data is based on a complete theory, it poses restrictive conditions for the resolution of problems: it requires that variables be single-valued (the value of a variable for an object is a unique and specific).
Recent evolutions in the information system have made it possible to find increasing and more complex data which need a more in-depth formalization than the one indicated in the usual rectangular table. The later does not take into account the possible variability of description as well as the uncertainty concerning certain variables or certain objects. A new formalism called symbolic objects has been developed to represent complex data like concepts, skills (see [1,2]). These objects concern complex data and provide new skills at the exit in the form of symbolic objects.
The techniques of factorial analysis (see [3,4]) which are data reduction and representation methods, are well known and well used. Certain stakeholders have extended these methods to symbolic objects by using the coding and decoding techniques (read [5,6]). The issue of multiple factorial analysis (MFA) is of particular interest to us (see [7,8]). A priori, this concerns the case where there is a group structure on variables. Its problem is enhanced by the characterization of groups and the search for a typology of groups of variables. To our knowledge, this method is not yet applied to symbolic objects.
In this article, we extend the MFA to a symbolic data base whose variables are structured into groups. It is a generalization of the MFA basic principle on the one hand, and the principle components analysis (PCA) techniques on the other hand (see [9]). We conclude this document with an application of the method presented to poverty data.
2. Symbolic Data Base
2.1. General Context
A symbolic data base (SDB) is considered as represented in the Table 1 and made up of triplet 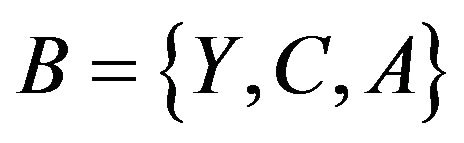 with
with  representing all the I objects,
representing all the I objects,
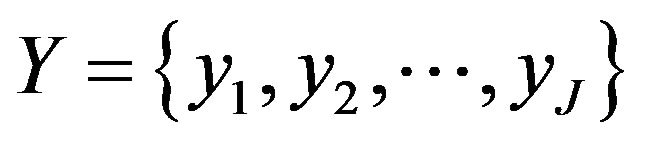 and
and 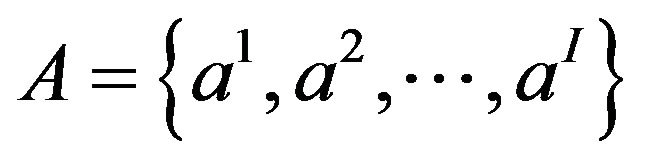 representing respectively the set of the J variables and the assertion objects used to describe I objects. We suppose that the SDB is associated with a measured space
representing respectively the set of the J variables and the assertion objects used to describe I objects. We suppose that the SDB is associated with a measured space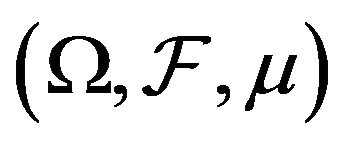 an
an ![]() algebra
algebra ![]() on C,
on C, 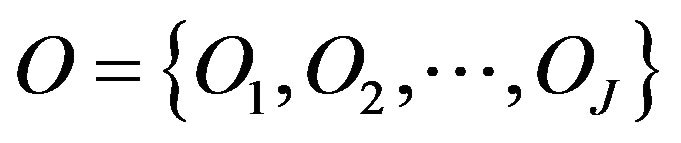 where
where
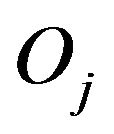 is the space of observation of the variable
is the space of observation of the variable
 . This space includes an tribe
. This space includes an tribe . Let
. Let
 be a set of measurable functions defined on
be a set of measurable functions defined on 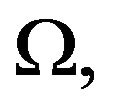 deriving their value from the measurable spaces
deriving their value from the measurable spaces  and used to describe all the
and used to describe all the ![]() objects. For
objects. For 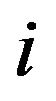
from 1 to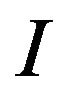 ,
, 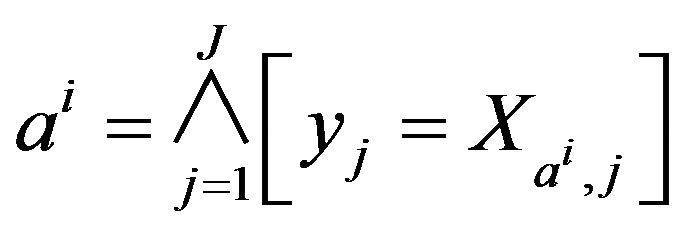
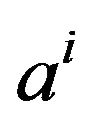 is a Boolean assertion so that from
is a Boolean assertion so that from  from
from 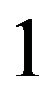 to
to![]() , there is a measurable part
, there is a measurable part  so that we can have
so that we can have
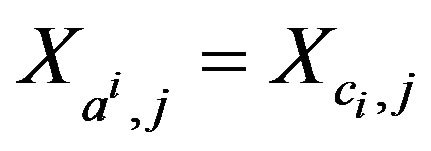 and
and 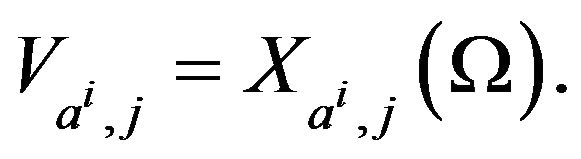 In practice, it is written
In practice, it is written
 (1)
(1)

Table 1. Symbolic data base.
The observation space is therefore the product space
 This space includes an product tribe
This space includes an product tribe
 To proceed, it is supposed that the descriptors are quantitative, i.e that
To proceed, it is supposed that the descriptors are quantitative, i.e that  is a part of
is a part of .
.
Thus, it is generalized that 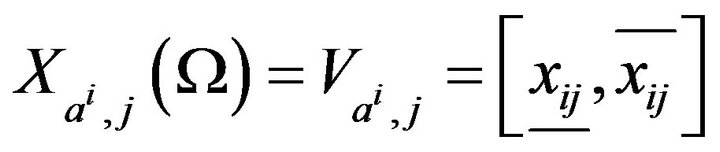
where ![]() represent respectively the minimum and maximum values per
represent respectively the minimum and maximum values per 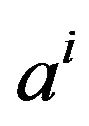 object for the
object for the  variable. Consequently, we shall treat the Boolean assertions whose SDB is indicated in the following Table 2.
variable. Consequently, we shall treat the Boolean assertions whose SDB is indicated in the following Table 2.
2.2. Group Structure
We shall assume that the J variables are divided into K groups with 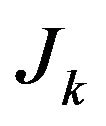 as the number of k group variables;
as the number of k group variables; 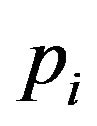 the weight associated with the assertion object
the weight associated with the assertion object 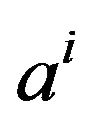 and
and  the weight of the
the weight of the  variable. We shall designate
variable. We shall designate 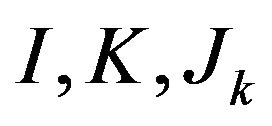 as the set and its cardinal. Let us consider
as the set and its cardinal. Let us consider 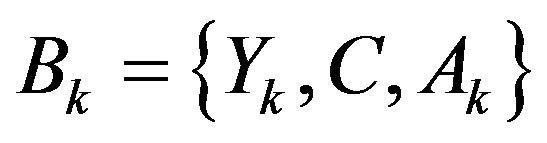 as the symbolic data base derived from
as the symbolic data base derived from 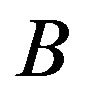 but reduced from the
but reduced from the 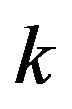 group variables denoted
group variables denoted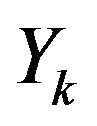 . For i from 1 to I, the
. For i from 1 to I, the  object for the k group is represented by the assertion
object for the k group is represented by the assertion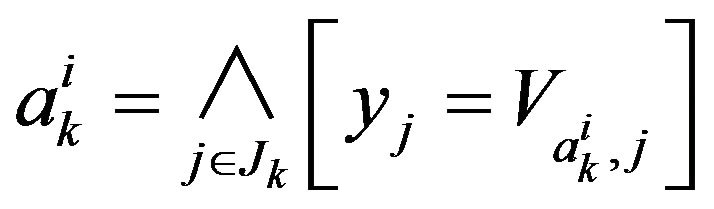 . Formula (1) may be re-written as follows, while taking into consideration the existence of the following groups:
. Formula (1) may be re-written as follows, while taking into consideration the existence of the following groups:

2.3. Objective
Like in the traditional case, the MFA based on symbolic data corresponds to the following three majors objectives:
1) Drawing up a typology of concepts, especially similar concepts from the point of view of all the variables after balancing the contribution of each group.
2) Comparing the typologies of individuals defined by groups of variables.
3) Exposing a typology of groups of variables and interpreting the proximities between them.
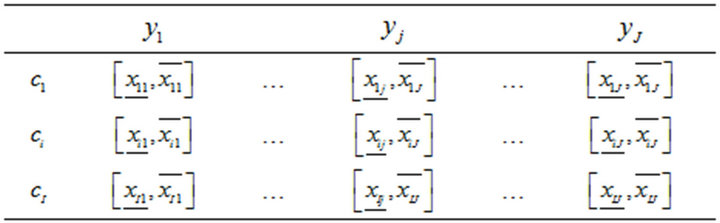
Table 2. Symbolic data base of boolean assertions.
However, taking into consideration the variability of objects adds an interesting element to this problem because coherence warrants us to provide exit elements in keeping with the variability.
3. Analysis and Interpretation
We shall present algorithm for a symbolic digital MFA. This approach essentially repeats the one used by the traditional MFA as well as that of the PCA on symbolic objects. The following stages shall be used:
1) Data coding;
2) PCA of groups;
3) Weighting of the data table;
4) PCA symbolic digital of all data;
5) Traditional MFA representation and interpretation;
6) Superimposed representation of symbolic objects and average cloud;
7) Representation of assertions of variables and symbolic factors of groups
3.1. Data Coding
Either ![]() all the assertions in the SDB, the m coding order is any C application to
all the assertions in the SDB, the m coding order is any C application to ![]() with values in
with values in 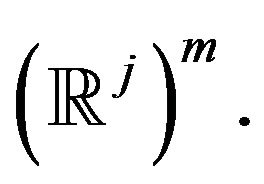
In this work, we shall therefore use the centre and summit methods which is referred to as characteristic coding and reconstitutive coding respectively.
An assertion object is graphically represented by a hypercube. The characteristic coding represents each object by a point which is the centre of gravity of the assertion object. The reconstitutive coding represents an object by 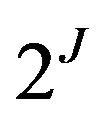 points which constitute the summit of the hypercube. Characteristic coding gives us the active elements of the analysis while reconstitutive coding gives the additional elements of the analysis that enable the reconstitution of the exit symbolic objects.
points which constitute the summit of the hypercube. Characteristic coding gives us the active elements of the analysis while reconstitutive coding gives the additional elements of the analysis that enable the reconstitution of the exit symbolic objects.
3.2. Weighting of Variables
Let X be the data table obtained after data coding. A J columns and 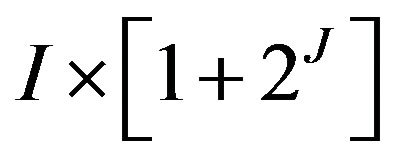 lines table is obtained where
lines table is obtained where
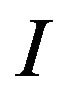 individuals are active and the others in addition. For each group, a principle components analysis (PCA) on the
individuals are active and the others in addition. For each group, a principle components analysis (PCA) on the 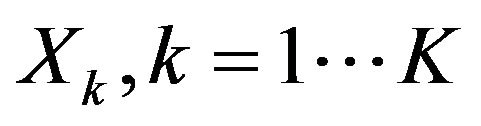 tables where
tables where 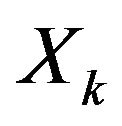 is the
is the 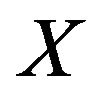 table reduced to the k group value. A series of
table reduced to the k group value. A series of
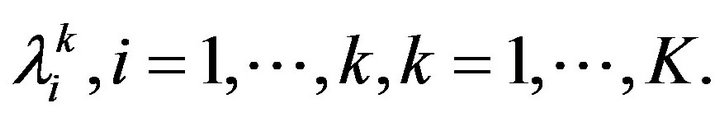 eigenvalues is obtained for each analysis. It is assumed that the real values in each group are classified in descending order. Each
eigenvalues is obtained for each analysis. It is assumed that the real values in each group are classified in descending order. Each 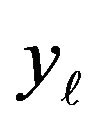 variable is weighted by
variable is weighted by 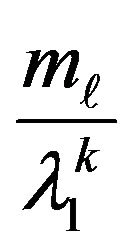 if the
if the 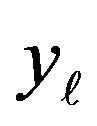 variable is derived from the
variable is derived from the 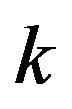 group. The weighted table is evaluated
group. The weighted table is evaluated .
.
3.3. Data Processing
Weighting conserves the internal structures of each group but changes the structure of the overall cloud (see [10]). In this case, it is referred to as the average cloud. As in the traditional case, we have represent equivalent objects by respective lines of the same 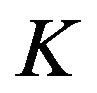 bases
bases 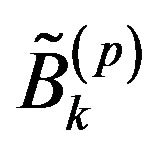 rank, with
rank, with 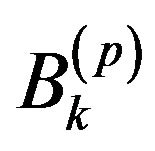 being the weighted
being the weighted 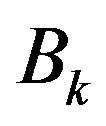 base.
base.

The 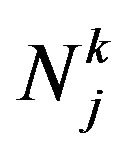 K clouds may be simultaneously represented in the
K clouds may be simultaneously represented in the  space of variables by breaking down
space of variables by breaking down  into direct sum spaces isomorphic to
into direct sum spaces isomorphic to 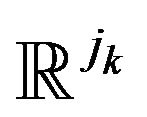 spaces.
spaces.
The average cloud is obtained by a homothetic transformation of the 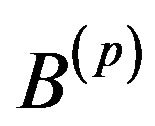
 relation weighted data base. It represents average individuals and average concepts in
relation weighted data base. It represents average individuals and average concepts in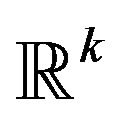 . The average cloud is obtained by a homothetic transformation of the
. The average cloud is obtained by a homothetic transformation of the 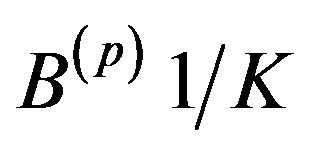 relation weighted data base. It represents average individuals and average concepts in
relation weighted data base. It represents average individuals and average concepts in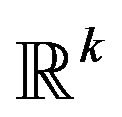 . Let us note
. Let us note 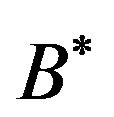 the SDB of the average cloud where
the SDB of the average cloud where  constitutes its restriction in the
constitutes its restriction in the 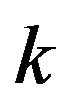 group.
group.
Proposition 1. The symbolic digital PCA of the  base leads to the same factors as the
base leads to the same factors as the 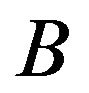 base characteristic coding MFA.
base characteristic coding MFA.
Proof. It is immediate. The 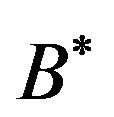 base is constructed to this effect. □
base is constructed to this effect. □
3.4. Canonic Variable
The re-writing of table 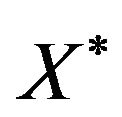 in the principle components base
in the principle components base 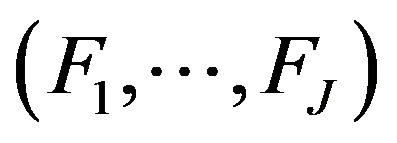 leads to a representation of objects by a new SDB
leads to a representation of objects by a new SDB 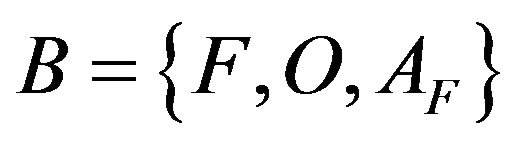 whose assertion is written
whose assertion is written
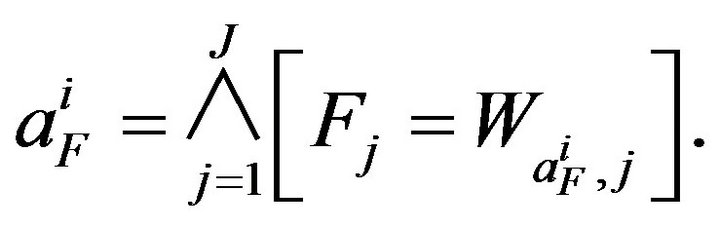 Assertions of the variables associated with concepts are written
Assertions of the variables associated with concepts are written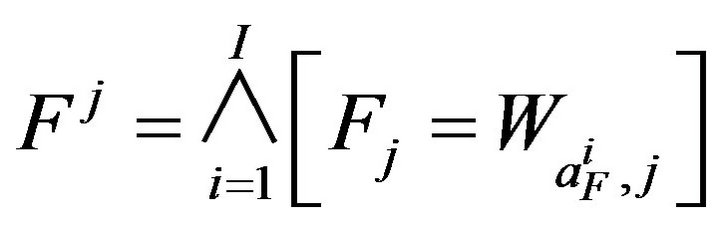 .
.
These factors are called canonic variables.
3.5. Superimposed Representation of Individuals and Concepts
3.5.1. Equivalent Assertions
A 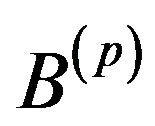 based
based 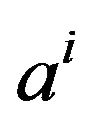 assertion is represented in each
assertion is represented in each 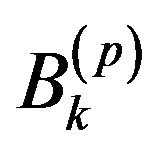 sub-base by
sub-base by 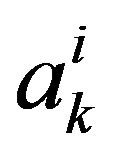 assertions which are called equivalent assertions associated with
assertions which are called equivalent assertions associated with . These are the different representatives in the
. These are the different representatives in the 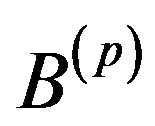 sub-bases of the same assertion.
sub-bases of the same assertion.
3.5.2. Superimposed Representation of Individuals
Here, individuals are described by the characteristic coding. An individual representing an object is represented by the expectation of unpredictable random. variable associated with the skill it represents. This representation no doubt has some shortcomings, but it gives us the first tendencies which are sometimes enough. In concrete terms, each group is projected with additional elements on the PCA of table 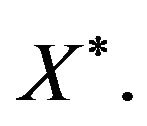
Proposition 2. Each individual (average individual) of table 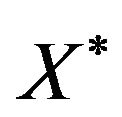 is the centre of gravity of individuals observed from the point of view of all groups.
is the centre of gravity of individuals observed from the point of view of all groups.
Proof. This is the property of traditional MFA. □
This proposition explains the notion of average cloud. The study of the attributes of variability of description indicated below will comfort us in this notion.
3.5.3. Superimposed Representation of Concepts
Symbolic digital PCA results will be used to obtain a superimposed representation of objects while taking into consideration variability. It based to the following proposition:
Proposition 3. Either 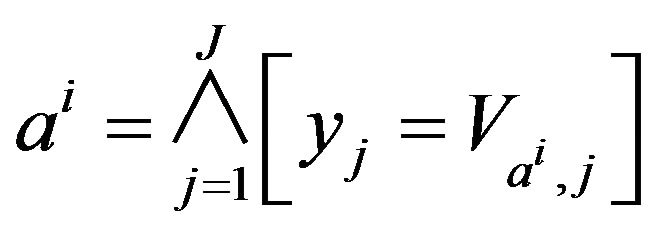 an assertion of BDS
an assertion of BDS . We note
. We note 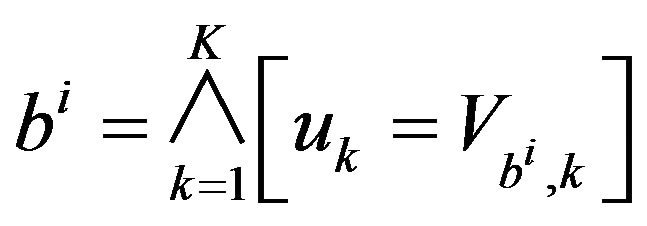 the assertion representing the
the assertion representing the ![]() objects in the space of the PCA principle components of this SDB. Let
objects in the space of the PCA principle components of this SDB. Let 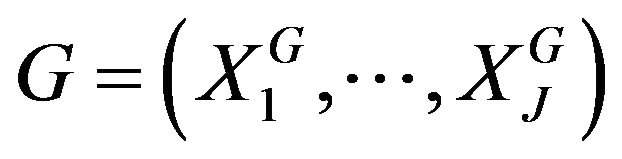 the centre of gravity of the characteristic coding and
the centre of gravity of the characteristic coding and  the kth component of the jth factorial axis. Thus we have:
the kth component of the jth factorial axis. Thus we have:
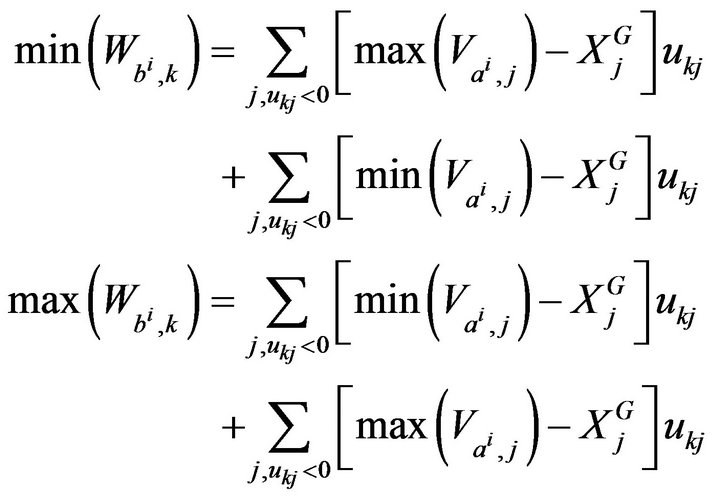
Proof. We note 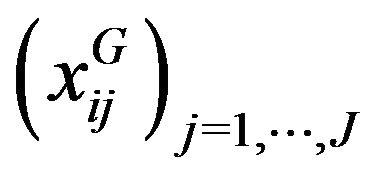 the coordinate of
the coordinate of 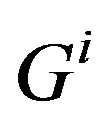
centre of gravity of 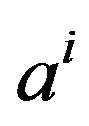 assertion, and
assertion, and  the coordinate of the image of
the coordinate of the image of 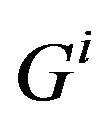 in the new basis. Let
in the new basis. Let 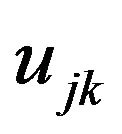 be the jth component of the kth factorial axis (denoted
be the jth component of the kth factorial axis (denoted ), we note
), we note 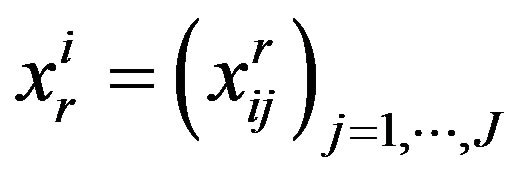 the coodinate of an elementary individual of
the coodinate of an elementary individual of 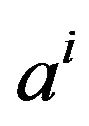 assertion for a point
assertion for a point 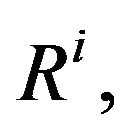 and
and 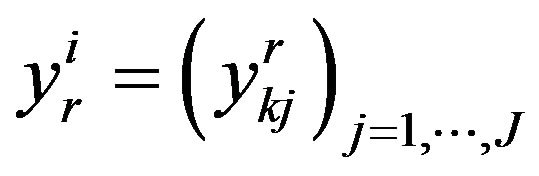 his coordinate in the new basis.
his coordinate in the new basis.
We have:
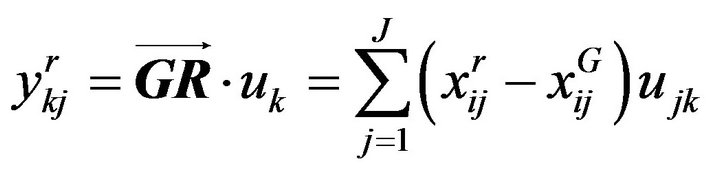
then
as  depend of
depend of  we have
we have
Therefore
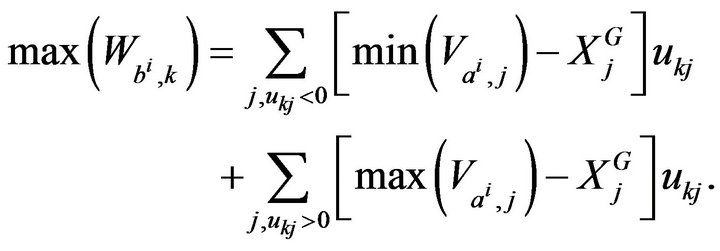
With the similar methode, we have
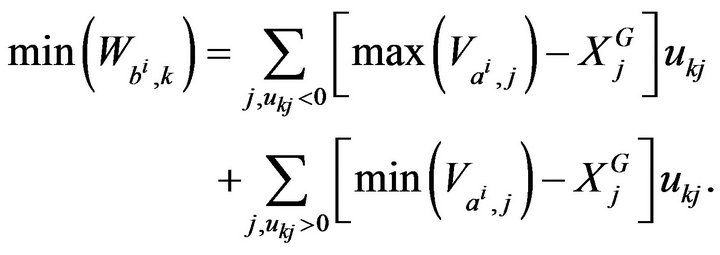
□
This lead that the 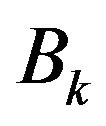 representing group
representing group 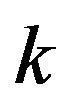 will be projected successively with additional elements on the
will be projected successively with additional elements on the 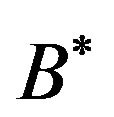 base symbolic digital PCA. The superimposed representation on the same factorial plan enables us to generally observe the position of an object, and the point of view of each group by using variability. We then have the following result :
base symbolic digital PCA. The superimposed representation on the same factorial plan enables us to generally observe the position of an object, and the point of view of each group by using variability. We then have the following result :
Proposition 4. Either 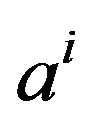 an assertion object represented in
an assertion object represented in 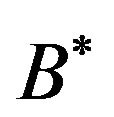 by
by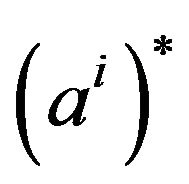 . Let us note
. Let us note  the
the 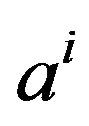 assertion observed from the
assertion observed from the  group point of view. In the
group point of view. In the 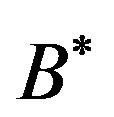 base, the
base, the 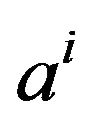 assertion is written
assertion is written
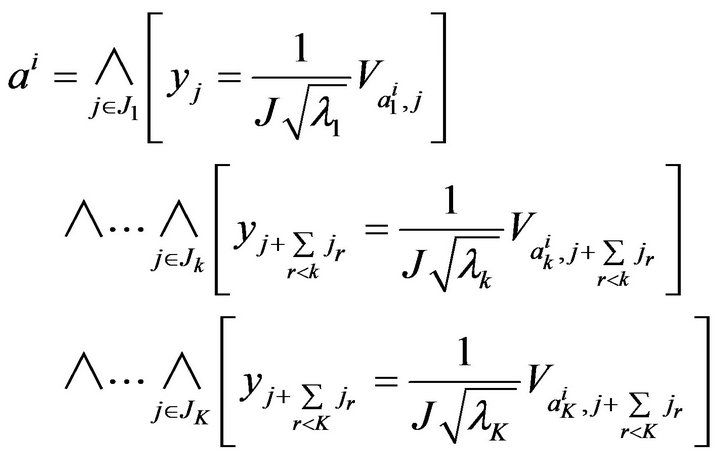
Either 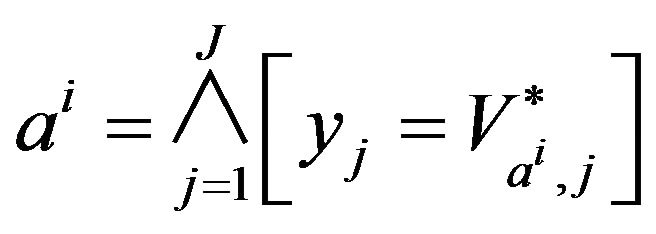 we note
we note
 the assertion representing the
the assertion representing the ![]()
object from the k group point of view in the space of the PCA principle components of this SDB. Either
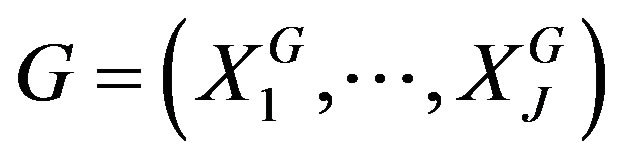 the centre of gravity of
the centre of gravity of , and
, and 
the kth component of the jth factorial axis. Thus we have:

Proof. This is the consequence of the notations of the previous proposition. □
The representation of superimposed objects in the canonic base (that of factors) therefore respects the principle of centres of gravity. The hypercube representing an object is thus the centre of gravity of the hypercubes representing the same individual from the point of view of different groups. The MFA symbolic digital algorithm helps to preserve this essential property.
3.6. Representation of Variables and Assertions of Variables
The symbolic digital MFA enables us to define many representatives that contribute to the illustration of factors in the general analysis as well as in the different groups. The determination of the main factors of groups and the general analysis lead to many representations of variables and assertions of variables. The superimposed representation of these factors (as assertions of variables) on canonic variables then helps to find and interpret common factors and specific factors.
3.6.1. Representation of Variables and Assertions of Variables
The conduct of the MFA symbolic digital pre-supposes  factorial analysis (the K groups and the average cloud). Two representations can be made for each of these analyses: a representation of variables (dual analysis of centres of gravity) and an analysis of assertions of variables taking into account variability. These representations clearly bring out the main variability factors of groups and the factors of general analysis.
factorial analysis (the K groups and the average cloud). Two representations can be made for each of these analyses: a representation of variables (dual analysis of centres of gravity) and an analysis of assertions of variables taking into account variability. These representations clearly bring out the main variability factors of groups and the factors of general analysis.
3.6.2. Superimposed Representation of Factors (as Assertions of Variables) on Canonic Variables
This representation is the result of a MFA traditional representation which consists in highlighting the main variability factors of groups in the form of additional variables over canonic variables. But in symbolic data analysis, these variability factors are also expressed as assertions of variables and the representation of these assertions of variables over the canonic variables calls for an original observation. The position and collection of assertions of variables give us precious indications on their importance and the link between the different groups.
3.6.3. Link between Groups: Representation Quality of Groups
This is a traditional indicator in MFA. It is a representation of groups on canonic factors. The coordinates of an axis group is the combined inertia of the group’s variables on the corresponding MFA axis of table . For the two groups
. For the two groups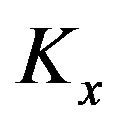 . and
. and , we have
, we have
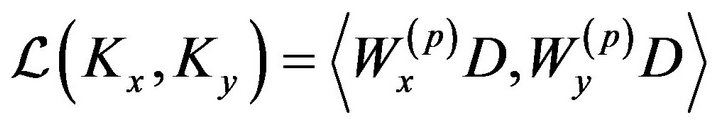 where D is the diagonal
where D is the diagonal
 matrix of the weight of individuals and
matrix of the weight of individuals and 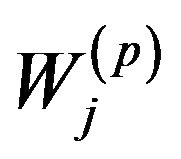 is the matrix of scalar products between the individuals of group
is the matrix of scalar products between the individuals of group  for the
for the 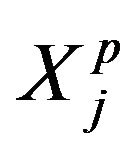 weighted matrix.
weighted matrix.
A symbolic representation may be proposed for it. Each assertion of variables can be coded into many variables whose projection over canonic variables results in a minimum value and a maximum value. The variability associated to a group will therefore be displayed by two values: the sum of the minimum inertia of the group’s variables and the sum of its maximum inertia.
The representation of groups is done in the  space.
space.
3.7. The Notion of Common Factor and Specific Factor
MFA helps to portray the characteristics of groups compared to the canonic variables (also referred to as factors). A common (or specific) factor to the MFA symbolic digital will be the common factor associated to the traditional MFA of centres of gravity.
4. Poverty Data
4.1. Presentation
The data is drawn from the first Cameroonian survey in households (ECAM I) conducted in 1996 by the National Institute of Statistics. The sample is made up of 1800 households with a total of 10230 individuals. The analysis is done on 13 continuous variables out of which 10 are active and 3 illustrative (see Table 3).
The average poverty line is used to establish the difference between poor and non poor individuals. We shall consider 10 classes of individuals with 5 poor classes organized in descending order from very poor to less poor individuals and 5 classes of non poor individuals organized in ascending order from less rich to very rich individuals. These classes constitute the concepts that we shall analyze. The groups of variables are regions. For presentation purposes, they shall be presented on a line and not in columns. An overview of the SDB for the Adamawa Region for three variables shows the following Table 4.
4.2. Analysis and Interpretation
After the algorithm application, the following results are obtained:
4.2.1. Inertia of the First Six Eigenvalues
Please see Table 5.
4.2.2. Relationship between General Variables and Groups
The F1 variable is the variable which extracts the most important inertia from all groups. The other variables convey specific information to certain regions (see Table 6).

Table 3. Variables of ECAM1.

Table 4. An overview of SDB of ECAM1.
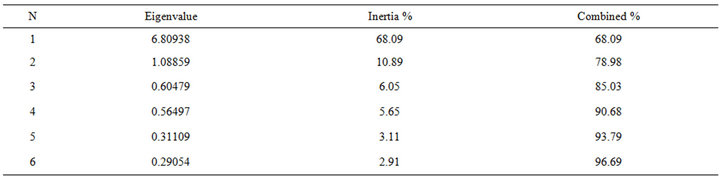
Table 5. Histogram of eigenvalues.
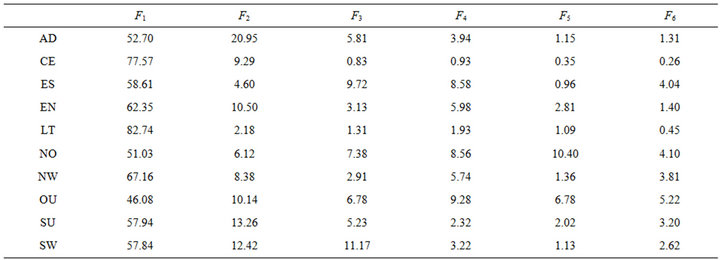
Table 6. Relationship between general variables and groups.
4.2.3. Inter-Inertial/Total Inertia Relationship
Table 7 shows that on the first axis, there is a close proximity between equivalent classes. Broadly speaking, these equivalent classes have similar behaviours in their expenditure habits. The same phenomenon is observed in the descending values of r, on the 4th, 2nd, 6th and 3rd axes.
4.2.4. Degree of Resemblance between Groups and General Variables: Common and Specific Factors
The first MFA component is a factor common to all the

Table 7. Inter-inertial/total inertia relationship.
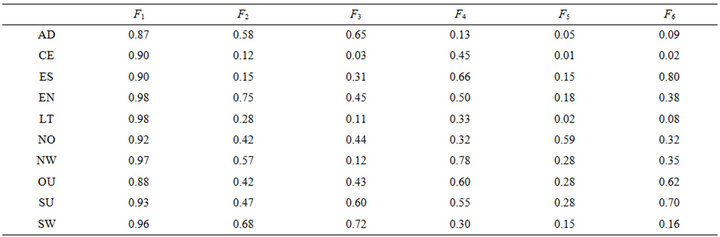
Table 8. Degree of resemblance between groups and general variables.
10 regions. The second factor is common to the FarNorth and South-West regions. The 3rd factor is specific to the South-West and Adamawa regions (see Table 8).
REFERENCES
- E. Diday, “Introduction to the Symbolic Data Analysis,” Cahiers du CEREMADE, No. 8823, 1988.
- E. Diday, “From the Objects of the Data Analysis to Those of the Analysis of Knowledge, Symbolic and Numeric Induction from Data,” Cépadues, 1991.
- L. Lebart, A. Morineau and Mr. Piron, “Multidimensional Exploratory Statistics,” 3rd Edition, DUNOD, Paris, 2000.
- M. Volle, “Data Analysis,” Economica, Paris, 1981.
- J. F. Martin, “Fuzzy Coding and Its Applications in Statistics,” Thesis, University of Pau, Pau, 1980.
- F. J. Gallego, “Fuzzy Coding in Correspondence Analysis,” Cahiers de l’Analyse des Données, Vol. 13, No. 2, 1980, pp. 413-430.
- J. Pagès and B. Escofier, “Simple and Multiple Factorial Analysis,” DUNOD, Paris, 1990.
- B. Escofier and J. Pajes, “Multiple Factorial Analysis, Objectives, Methodology and Interpretation,” 2nd Edition, Wiley, Paris, 2005.
- P. Cazes, A. Chouakria, E. Diday and Y. Schektman, “Extension of Principal Component Analysis to Interval Data,” Revue de Statistique Appliquée, Vol. 45, No. 3, 1997, pp. 5-24.
- B. Ahanda Tang, “Extension of Factorial Analysis to Symbolic Data,” Thesis, University of Paris, Paris, 1998.

