Applied Mathematics
Vol. 4 No. 2 (2013) , Article ID: 28219 , 15 pages DOI:10.4236/am.2013.42059
Theoretical Assessment of the Transmission Dynamics of Leprosy
Modelling Biomedical Systems Research Group, Department of Applied Mathematics, National University of Science and Technology, Bulawayo, Zimbabwe
Email: edward.chiyaka@gmail.com, tmuyendesi@gmail.com, philimon.nyamugure@nust.ac.zw, farikayi.mutasa@nust.ac.zw
Received September 7, 2012; revised January 10, 2013; accepted January 17, 2013
Keywords: Leprosy; Mycobacterium leprae; Mathematical Model; Multibacillary
ABSTRACT
Leprosy is a communicable disease which can cause hideous deformities to the afflicted and social stigmatization to them and their families. The continued high endemicity of leprosy in pockets of Sub-Saharan Africa is a source of bafflement to researchers. In this paper, we investigate non-compliant behavior by patients on treatment and possible inadequacy of the prescribed treatments as the reason for the persistence of the disease in the region. We construct theoretical, deterministic mathematical models of the transmission dynamics of leprosy. These models are modified to encapsulate non-compliance and inadequate treatment. The models are then analyzed to gain insight into the qualitative features of the equilibrium states, which enable us to determine the basic reproduction number. We also employ analytical and numerical techniques to investigate the impact of non-compliance and inadequate treatment on the transmission dynamics of the disease. Our results show that, as long as there is treatment, leprosy will eventually be eliminated from the region and that the disposition under investigation only serves to slow the rate at which the disease is eradicated.
1. Introduction
Leprosy, under guidelines set by the World Health Organization (WHO), has been successfully eliminated elsewhere. Most previously highly endemic countries have now reached elimination (defined as a registered prevalence rate of less than one case per 10,000 populations). At the beginning of 2009, pockets of high endemicity still remained in Angola, Central African Republic, Democratic Republic of Congo, India, Madagascar, Mozambique, Nepal, United Republic of Tanzania, and Brazil. These 9 countries account for 88% of all new cases. There were 213,036 new cases recorded from 121 countries at the beginning of 2009 [1]. Leprosy or Hansen’s disease is a chronic disease which has plagued mankind for at least 4000 years. It is caused by the pathogen, Mycobacterium leprae (M. leprae). Leprosy is principally a granulomatous disease of the peripheral nerves and mucosa of the upper respiratory tract. Skin lesions are the primary external sign. Unless properly treated, leprosy can be relentlessly progressive, causing permanent damage to the skin, nerves, limbs and eyes. The victims often die of some other disease and only a few live until they succumb to the wasting effects of leprosy itself. The age-old social stigma associated with the advanced form of leprosy lingers in many areas, and remains a major obstacle to self-reporting and early treatment.
Leprosy is a communicable, slow progressing disease which is transmitted by contact between infected and healthy persons. Nasal secretions of untreated cases are the main exit route of the pathogen which is believed to gain entrance into the susceptible body through membranes lining the nose or through breaks in the skin. Living in close proximity with an infected individual seems necessary for one to contact the disease. Most individuals exposed to M. leprae do not develop clinical features; the infection quietly dies out. If the infection progresses, the disease manifests in two extreme forms; tuberculoid and lepromatus leprosy. Effective chemotherapy treatments are available for all manifestations of leprosy. When a patient begins treatment, he/she ceases to be infective in as little as 72 hours and can gradually resume normal life while continuing the chemotherapy treatment for periods of 6, 12 or 24 months depending on the type of manifestation. Reversal reactions, absenteeism and non-compliance are some factors that complicate the curing process of any particular disease. If the disease is not treated properly, a relapse is imminent and the disease can be perilously progressive. A relapse is defined as the recurrence of the disease after completion of the treatment [2].
2. Transmission and Pathogenesis
Nasal secretions of untreated lepromatus patients are teeming with bacilli and constitute the main source of infection, which occurs when the M. leprae invades the susceptible body via the nasal mucosa and spreads to the peripheral nerve Schwann cells and skin macrophages. M. leprae is also suspected to invade the body via broken skin. The skin of lepromatous patients is a possible exit route for the pathogen: lepromatous cases show large numbers of M. leprae deep down in the dermis. The pathogen is known to be a stable and hardy organism which can survive in the environment for up to 5 months [3,4]. Leprosy is not hereditary but in few cases, infection actually takes place through the placenta. M. leprae can also be transmitted from mother to child via breast milk. For one to contract the disease, frequent and close contact with an infected person has been shown to be necessary. Since a contagious individual may infect close contacts rapidly, opportunities to transmit M. leprae may decrease with longer duration of the disease. Only small minorities of the exposed develop leprosy; the majority will have a sub-clinical infection and presumably develop protective immunity [3]. It is estimated that 95% of the exposed are able to clear the infection this way [4].
Transmission studies are difficult because of the unique biology of the M. leprae and long incubation period of the disease. In leprosy, both the reference points for measuring the incubation period and the times of infection and onset of disease are difficult to define; the former because of the lack of adequate immunological tools and the latter because of the disease’s slow onset. The incubation period is estimated to be between 2 - 5 years and 8 - 12 years for tuberculoid and lepromatus cases respectively [4]. The minimum incubation period reported is as short as a few weeks and this is based on the very occasional occurrence of leprosy among young infants. One of the greatest uncertainties in leprosy studies is that individuals incubating the disease may already harbor many bacilli, and it is possible that these individuals already transmit M. leprae to others long before the onset of the disease, given its long incubation period. Leprosy has an insidious onset and the source of infection in an infected individual is rarely identified. Studies detecting M. leprae deoxyribonucleic acid (DNA) by polymerase chain reaction (PCR) in nasal secretions have shown that it is carried by normal individuals and contacts in endemic countries (in Ethiopia, 6% of the population, in 1998) [3]. In leprosy, the clinical features are determined by the host’s immune response. In those infected who do develop the disease, a spectrum of immune responses is seen. At one end of the spectrum, characterized by strong cell mediated immunity towards M. leprae, is Tuberculoid leprosy. These patients have low bacillary loads. At the other pole is lepromatous leprosy, which is characterized by the absence of a cell mediated immune response and high bacillary loads in its cases. If Tuberculoid leprosy is left untreated it eventually resolves spontaneously, or if the patient has a less vigorous cellular immune response to the M. leprae bacteria, the disease may progress to a borderline leprosy. Lepromatus leprosy is the most severe; it is relentlessly progressive and unlike Tuberculoid leprosy which may or may not be infectious, its cases are definitely so. This form of leprosy is responsible for the gross deformities associated with the disease.
Worldwide, 1 - 2 million persons are permanently disabled as a result of Hansen’s disease [5]. Between these two extremities, there are borderline patients with varying immunological responses and bacterial loads. Borderline patients are immunologically unstable and most progress towards lepromatus leprosy. They are also at risk of violent reversal reactions. These are delayed hypersensitivity reactions against M. leprae antigens and the result is elimination of mycobacteria which is achieved at the expense of severe local tissue damage, in particular to nerves. Nerve involvement is important in leprosy. Peripheral nerve damage occurs across the spectrum and it can occur before, during or after treatment. In an Ethiopian study, 55% of patients had some degree of nerve function impairment at diagnosis [3]. Reversal reactions certainly complicate the nerve conditions and may lead to transient paralysis of the nerves. Delay in diagnosis may result in permanent nerve damage. In Nigeria 68% of patients had delays of more than a year before starting treatment. Of these, 37% had consulted folk healers who advised them not to seek medical help [3].
3. Model Formulation
We propose a deterministic SEIR model with respect to paucibacillary leprosy (PB) and an SEI model with respect to multibacillary leprosy (MB) when no treatment and control measures are put in place. The model divides the population concerned into the following five, time dependent subgroups or compartments:
 —susceptible individuals who are yet to come into contact with the infection.
—susceptible individuals who are yet to come into contact with the infection.
 —individuals who have been infected by leprosy but not yet infectious nor showing any symptoms,
—individuals who have been infected by leprosy but not yet infectious nor showing any symptoms, — infectious class of individuals whose infection has progressed to paucibacillary leprosy,
— infectious class of individuals whose infection has progressed to paucibacillary leprosy, — infectious class of individuals whose infection has progressed to multibacillary leprosy, and
— infectious class of individuals whose infection has progressed to multibacillary leprosy, and —non-infectious group of people who have successfully recovered from the disease and are immune to re-infections.
—non-infectious group of people who have successfully recovered from the disease and are immune to re-infections.
Individuals move from one class to the other as their status with the disease evolves. Let  be the total number of people in the population at any time
be the total number of people in the population at any time , then:
, then:
 and
and 
represent the probability that a randomly selected individual has multibacillary and paucibacillary leprosy, respectively. Let the probability of infecting a susceptible during interaction be  and
and  for MB and PB cases, respectively. The probability of a susceptible being infected by an MB and a PB case is
for MB and PB cases, respectively. The probability of a susceptible being infected by an MB and a PB case is
 and
and correspondingly. The force of infection for the disease can be expressed as
correspondingly. The force of infection for the disease can be expressed as

Infection is transmitted to the susceptible persons through successful contacts with either a paucibacillary or multibacillary patient. Class  is increased by graduands from the susceptible class and decreases by natural death, progression of the infections to either PB or MB leprosy and by subsequent recoveries by some of its members. For patients who move to class
is increased by graduands from the susceptible class and decreases by natural death, progression of the infections to either PB or MB leprosy and by subsequent recoveries by some of its members. For patients who move to class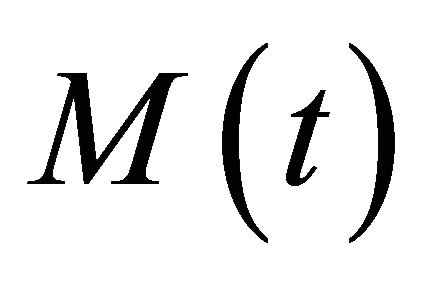 , they either die naturally or due to leprosy related complications or eventually succumb to the wasting effects of the disease itself. Once an individual has progressed to compartment
, they either die naturally or due to leprosy related complications or eventually succumb to the wasting effects of the disease itself. Once an individual has progressed to compartment  he/she eventually recovers and moves to class
he/she eventually recovers and moves to class  where he/she is immune to reinfections and is non-infectious. Assumptions of the model are:
where he/she is immune to reinfections and is non-infectious. Assumptions of the model are:
• The population is homogenous and each individual is equally likely to interact with the other.
• Transmission follows the mass action principle; if
 is the number of infectious individuals and
is the number of infectious individuals and  and
and  have their usual meaning, then the standard incidence per unit time is of the form
have their usual meaning, then the standard incidence per unit time is of the form , for
, for .
.
• Transmission is only through interactions between the susceptible person and either a PB or MB individual.
• Patients who recover from the disease become immune to re-infections and are no longer infectious.
• No individual is naturally or artificially immune to the disease, immunity is only acquired through recovery from infection.
• Paucibacillary is not fatal, it is self limiting and all its cases eventually recover.
• Multibacillary is relentlessly progressive and is fatal.
• MB patients are not isolated thus continue to be infectious until they pass away.
• There is no migration, new recruits enter the population through birth and the population decreases by natural or disease induced mortality.
Parameters: —the probability of an MB case infecting a susceptible during interaction.
—the probability of an MB case infecting a susceptible during interaction. —the probability of an PB case infecting a susceptible during interaction.
—the probability of an PB case infecting a susceptible during interaction. —the rate of progression from
—the rate of progression from  to multibacillary leprosy.
to multibacillary leprosy. —the rate of progression from
—the rate of progression from  to paucibacillary leprosy.
to paucibacillary leprosy. —the recovery rate for the asymptomatic patients in
—the recovery rate for the asymptomatic patients in .
. — the recovery rate for the PB patients.
— the recovery rate for the PB patients. —the natural death rate,
—the natural death rate, —disease induced mortality rate for MB patients, and
—disease induced mortality rate for MB patients, and —birth rate.
—birth rate.
The population transfer among compartments is schematically depicted in the transfer diagram in Figure 1.
3.1. Model Equations
The evolution of the number of individuals in each compartment is described by the following system of ordinary differential equations:

Figure 1. Model diagram of the mathematical model for leprosy transmission.
 (1)
(1)
Initial conditions of system (1) are

and , where
, where  and
and  are all greater or equal to zero and
are all greater or equal to zero and

3.2. Positivity of Solutions
The variables in (1) represent sub-populations of individuals and therefore, should be positive or zero for all . If this condition is not met, the model should be discarded as it violates a basic aspect of scientific reality. Let
. If this condition is not met, the model should be discarded as it violates a basic aspect of scientific reality. Let  be an
be an ![]() -dimensional space, for
-dimensional space, for . If
. If  is a subset of
is a subset of , it is said to be positive invariant with respect to a system of ordinary differential equations if a trajectory that starts in
, it is said to be positive invariant with respect to a system of ordinary differential equations if a trajectory that starts in  remains there forever. Positive invariance of the non-negative orthant of
remains there forever. Positive invariance of the non-negative orthant of  for system (1) is assured if no trajectory can leave by crossing through one of its faces. The following theorem ensures that system (1) is well posed such that a solution with a non-negative initial point remains non-negative for
for system (1) is assured if no trajectory can leave by crossing through one of its faces. The following theorem ensures that system (1) is well posed such that a solution with a non-negative initial point remains non-negative for .
.
Theorem 1 The solutions of (1) are strictly positive for all  and for all sets of initial conditions
and for all sets of initial conditions
 and
and  with strictly positive components.
with strictly positive components.
Proof. We need to show that if a solution starts from a strictly positive point, the solution is strictly positive for . To see this strict positivity, we proceed as follows:
. To see this strict positivity, we proceed as follows:
From the first equation, since , we have
, we have

where

After integrating, we obtain;

Similar analysis for the second and third equation yields;

and

Analyzing the last two equations also shows that the variables  and
and  are also positive. Hence, we conclude that solutions
are also positive. Hence, we conclude that solutions  and
and  are always positive for all
are always positive for all .
.
3.3. Equilibrium States
The equilibrium states for the basic model are found by setting the right hand side of system (1) equal to zero. The model admits two equilibrium points, the disease free and the endemic equilibrium states.
3.3.1. Disease Free Equilibrium State
At this steady state, there are no individuals exposed to M. leprae, no one is afflicted or has recovered from the disease, hence there is no infection in the population. Thus system (1) has a disease free equilibrium (DFE)

The stability of this steady state can be analyzed through the determination of the basic reproduction number, .
.
3.3.2. Basic Reproduction Number
The basic reproduction number,  , is defined as the average number of secondary infections produced by one primary infection in a wholly susceptible population during his/her entire life as infectious [6]. If
, is defined as the average number of secondary infections produced by one primary infection in a wholly susceptible population during his/her entire life as infectious [6]. If , then on average an infected individual produces less than one new infected individual over the course of its infectious period, and the infection cannot grow. Conversely, if
, then on average an infected individual produces less than one new infected individual over the course of its infectious period, and the infection cannot grow. Conversely, if , then each infected individual produces, on average, more than one new infection, and the disease can invade the population [7]. In this study,
, then each infected individual produces, on average, more than one new infection, and the disease can invade the population [7]. In this study,  refers to the average number of secondary M. leprae infections produced by either a typical multibacillary or a paucibacillary patient in a totally susceptible population during his/her course of infectiousness. To calculate
refers to the average number of secondary M. leprae infections produced by either a typical multibacillary or a paucibacillary patient in a totally susceptible population during his/her course of infectiousness. To calculate , we follow the method outlined by Wartmough, 2008 [8]. We find our basic reproduction number to be
, we follow the method outlined by Wartmough, 2008 [8]. We find our basic reproduction number to be

We can express  as the sum of two quantities,
as the sum of two quantities,  , where
, where

and

The two quantities represent the reproductive numbers for the multibacillary and for the paucibacillary, respectively. On average, in a totally susceptible population, a primary MB patient produces  new M. leprae infections whilst a PB index case generates
new M. leprae infections whilst a PB index case generates  secondary M. leprae infections in their lifetimes as infectious. To keep leprosy under control, the numerical value of
secondary M. leprae infections in their lifetimes as infectious. To keep leprosy under control, the numerical value of  should be below unity. From the analysis of
should be below unity. From the analysis of  we can make a few general deductions and recommendations concerning transmission of leprosy.
we can make a few general deductions and recommendations concerning transmission of leprosy.
To assess the effect of the rates of progression from latent infection  to either MB or PB, we difnferentiate
to either MB or PB, we difnferentiate  with respect to
with respect to  and
and  with respect to
with respect to . This gives;
. This gives;

and

We note that rates of progression from latent infection to infectious leprosy significantly contributes to transmission of the disease. An effective control measure would be to treat the infection still in the latent stage; however, no suitable method for diagnosis of sub-clinical leprosy exists, as such this control measure is infeasible at present. We also note that the probability of a successful infection during an interaction between an infectious person ( and
and ) and a susceptible individual has a direct effect on
) and a susceptible individual has a direct effect on . Hence, education of the masses about leprosy transmission would greatly reduce this probability.
. Hence, education of the masses about leprosy transmission would greatly reduce this probability.
3.3.3. Endemic Equilibrium State
When the conditions for the global asymptotic stability of the DFE are not met, system (1) admits a unique endemic equilibrium state which exists if and only if . The endemic equilibrium is given by
. The endemic equilibrium is given by

where
 (2)
(2)
where
 and
and .
.
This steady state is subject to the condition that
 or
or .
.
It can also be shown that this steady state is biologically sensible if .
.
3.3.4. Existence of the Endemic Equilibrium
To show that the endemic equilibrium indeed exists for system (1) if , we first express the equilibrium point in terms of
, we first express the equilibrium point in terms of  as follows:
as follows:
 (3)
(3)
After substituting the expressions for  and
and  in the second equation of (1), we get
in the second equation of (1), we get
 (4)
(4)
where  and
and .
.
Solving equation (4), we get as one of the solutions  which corresponds to the disease free equilibrium. The other solution is
which corresponds to the disease free equilibrium. The other solution is . This solution exists for
. This solution exists for  since it is clear that
since it is clear that . Since
. Since , then
, then  and so
and so  if
if . The result of the existence of the endemic equilibrium for model system (1) can be summarized by the following lemma.
. The result of the existence of the endemic equilibrium for model system (1) can be summarized by the following lemma.
Lemma 1 The model system (1) always has a disease free equilibrium for  and a unique endemic equilibrium exists if
and a unique endemic equilibrium exists if .
.
3.3.5. Local Stability of the Endemic Equilibrium
The standard technique of determining the local stability of the endemic equilibrium is by linearization about the steady state and subsequent application of the RouthHurwitz analysis. Such an approach would be mathematically cumbersome for system (1). We therefore resort to the Center Manifold Theory as presented in Theorem 4.1 [Castillo-Chavez and Song, 2004][9], to establish the local asymptotic stability of the endemic equilibrium [10]. In order to apply the Center Manifold Theory, we make the following changes of variables:
Let

such that
 .
.
We now use the vector notation

and model system (1) can now be expressed in the form  such that:
such that:
 (5)
(5)
Using the Jacobian matrix of the above system at the disease free equilibrium, we obtain the model reproduction number

which is similar to the one we got previously. We choose  as our bifurcation parameter such that if
as our bifurcation parameter such that if , then
, then  and if
and if  then
then . We consider
. We consider  and solve for
and solve for  to get:
to get:

We shall denote  by
by  when
when .
.
The Jacobian matrix  has a simple zero eigenvalue, hence the Center Manifold Theory can be used to analyze the dynamics of system (5) near
has a simple zero eigenvalue, hence the Center Manifold Theory can be used to analyze the dynamics of system (5) near .
.
A right eigenvector associated with the zero eigenvalue exists and is given by  where
where

The left eigenvector associated with the zero eigenvalue at  is given by
is given by

where

We now use the following theorem whose proof is found in [9].
Theorem 2 Consider the following general system of ordinary differential equations with a parameter 
 (6)
(6)
where  is an equilibrium of the system, that is
is an equilibrium of the system, that is  for all
for all  and assume A1:
and assume A1:  is the linearization of system (5) around the equilibrium 0 with
is the linearization of system (5) around the equilibrium 0 with  evaluated at
evaluated at . Zero is a simple eigenvalue of
. Zero is a simple eigenvalue of  and other eigenvalues of
and other eigenvalues of  have negative real parts;
have negative real parts;
A2: Matrix  has a right eigenvector
has a right eigenvector ![]() and a left eigenvector
and a left eigenvector ![]() corresponding to the zero eigenvalue.
corresponding to the zero eigenvalue.
Let  be the
be the  component of
component of  and
and
 (7)
(7)
The local dynamics of (5) around  are totally governed by
are totally governed by ![]() and
and .
.
1) . When
. When  with
with ,
,  is locally asymptotically stable, and there exists a positive unstable equilibrium; when
is locally asymptotically stable, and there exists a positive unstable equilibrium; when ,
,  is unstable and there exists a negative and locally asymptotically stable equilibrium;
is unstable and there exists a negative and locally asymptotically stable equilibrium;
2) . When
. When  with
with ,
,  is unstable; when
is unstable; when ,
,  is locally asymptotically stable, and there exists a positive unstable equilibrium;
is locally asymptotically stable, and there exists a positive unstable equilibrium;
3) . When
. When  with
with ,
,  is unstable, and there exists a locally asymptotically stable negative equilibrium; when
is unstable, and there exists a locally asymptotically stable negative equilibrium; when ,
,  is stable and a positive unstable equilibrium appears;
is stable and a positive unstable equilibrium appears;
4) . When
. When  changes from negative to positive,
changes from negative to positive,  changes its stability from stable to unstable. Correspondingly a negative unstable equilibrium becomes positive and locally asymptotically stable.
changes its stability from stable to unstable. Correspondingly a negative unstable equilibrium becomes positive and locally asymptotically stable.
3.3.6. Computations of a and b
For system (5), the associated non-zero partial derivatives of  at the disease free equilibrium are given by
at the disease free equilibrium are given by
 (8)
(8)
Since all non-zero partial derivatives of  are negative and all
are negative and all  for
for  and 5, it follows from the above expressions that
and 5, it follows from the above expressions that .
.
For the sign of b, it is associated with the following non-zero partial derivatives of ,
,

We thus have .
.
Thus,  and
and . Using Theorem 2, item (4), we have established the following result which only holds for
. Using Theorem 2, item (4), we have established the following result which only holds for  but close to 1:
but close to 1:
Theorem 3 The unique endemic equilibrium guaranteed by Theorem 2 is locally asymptotically stable for  near 1.
near 1.
4. Model with Treatment
The first modern drug used in the chemotherapy of leprosy was Dapsone, in 1940, as monotherapy. Dapsone is only weakly bactericidal against M. leprae and it was considered necessary for patients to take the drug indefinitely. Evolving drug resistance and treatment failures when Dapsone was used led to the world’s only known anti-leprosy drug becoming virtually useless in the 1960s. Soon, it became clear that Dapsone resistance was on account of use of the drug as monotherapy. Worldwide increase in Dapsone resistance and the availability of equally effective drugs—Clofazimine and Rifampicin and from the experience in the therapy of tuberculosis (TB), led to the concept of multi-drug therapy (MDT) as a polychemotherapy for leprosy. Based on the theoretical considerations, recommendations were made to treat leprosy with multi-drug regimens [4,11]. In 1981, multi-drug therapy (MDT) was first recommended by WHO. MDT is comprised of Dapsone, clofazimine and rifampicin, which are bactericidal drugs [12]. Its characteristics are as follows:
1) The regimen includes drugs acting by different mechanisms, in order to prevent the emergence of drug resistance, and to be effective for strains of M. leprae resistant to any one of the three drugs.
2) The duration of MDT is limited in contrast to the lifelong duration of Dapsone monotherapy, to improve patient’s compliance. To make this possible, only bactericidal drugs are included as components.
3) Rifampicin is a key component because of its powerful bactericidal effect against M. leprae. It was to be administered only once per month under supervision, to ensure compliance and because of its high cost.
Two common regimens of MDT have been adopted, based on classification of leprosy into Multibacillary (or MB) and Paucibacillary (or PB). MB includes lepromatus cases and borderline cases associated with high bacillary loads. PB includes tuberculoid patients and borderline cases which are characterized by small bacterial loads. The first is a 24-month treatment for multibacillary cases using rifampicin, clofazimine, and dapsone. The second is a six-month treatment for paucibacillary cases, using rifampicin and dapsone. The duration of MDT for MB patients was shortened to 12 months, in 1998 on the recommendation of WHO. MDT is safe, effective and easily administered [13]. There are virtually no relapses of the disease if treatment is completed and no resistance of the bacillus to MDT has been detected. WHO estimates that early detection and treatment with MDT has prevented about four million people from being disabled. This suggests great cost-effectiveness of MDT as a health intervention, considering the economic and social loss averted [1]. Reversal reactions always complicate the curing process and WHO has stated that chemotherapy should not be stopped during a reaction. Relapses and persistent infections are not uncommon; they serve to complicate the curing process and extend the period over which an individual is infectious.
In this section, we investigate the situation in which leprosy patients have access to MDT chemotherapy. MDT is very effective and patients are no longer infectious in as little as 72 hours after beginning treatment. In other words, transmission of leprosy is interrupted almost immediately. We aim to examine the ideal situation; one in which all patients are compliant and are put on MDT until completely cured. There are no relapses or recurrences of the disease. Patients with a high initial bacterial index are treated until they test negative for M. leprae. Individuals who fail to recover from reversal reactions are put on lifelong MDT, thus they continue to be non-infectious even though the bacterium is persisting and can be considered removed.
4.1. The Model
This model divides the population into the following five time dependent compartments;  and
and —all of which are still defined as per the last section but
—all of which are still defined as per the last section but  now includes recoveries due to MDT treatment in addition to natural recoveries. Exposed class,
now includes recoveries due to MDT treatment in addition to natural recoveries. Exposed class,  is increased by individuals from the susceptible compartment who contact the disease. The majority of these naturally recover while other infecteds subsequently progress to either paucibacillary or multibacillary leprosy and the rest die of natural causes. MB patients, (in
is increased by individuals from the susceptible compartment who contact the disease. The majority of these naturally recover while other infecteds subsequently progress to either paucibacillary or multibacillary leprosy and the rest die of natural causes. MB patients, (in ) either recover under treatment or pass away due to both natural and disease induced mortality.
) either recover under treatment or pass away due to both natural and disease induced mortality.
• 4.1.1. Assumptions
• PB leprosy is not fatal and its cases recover naturally or due to the treatment.
• MB patients recover under treatment; however they are still subject to mortality due to disease related complications.
• Patients who recover naturally or under treatment become non-infectious and are immune to re-infections.
From the model (1), assumptions about the method of transmission and homogenous mixing of the population still hold. We also assume that no individual is naturally or artificially immune to the disease, immunity is only acquired through recovery from infection. Again, there is no migration; new recruits enter the population through birth and the population decreases by natural or disease induced mortality. Only two new parameters are included, which are —the recovery rate for MB patients, which is entirely due to treatment, and
—the recovery rate for MB patients, which is entirely due to treatment, and —the recovery rate for PB patients which includes both natural and recoveries under treatment. We retain the rest of the parameters from model (1), and maintain their definitions.
—the recovery rate for PB patients which includes both natural and recoveries under treatment. We retain the rest of the parameters from model (1), and maintain their definitions.
 (9)
(9)
Initial conditions for model system (9) are

and ; where
; where  and
and  are all greater than zero and
are all greater than zero and

4.1.2. Effective Reproductive Number
To calculate , we follow the method outlined by Wartmough [2008][8]. In our model, we can classify the
, we follow the method outlined by Wartmough [2008][8]. In our model, we can classify the  and
and  as the disease states. Thus,
as the disease states. Thus,

 can be expressed as the sum of two quantities:
can be expressed as the sum of two quantities:  where
where

and

are the respective effective reproductive numbers for the multibacillary and for the paucibacillary forms of the disease when there is treatment.
4.1.3. Analysis of the Effective Reproductive Number
From the analysis of  we can make a few general deductions and recommendations concerning transmission of leprosy with MDT treatment.
we can make a few general deductions and recommendations concerning transmission of leprosy with MDT treatment.
• To assess the effect of MDT treatment on the transmission of leprosy, we first differentiate ![]() with respect to the treatment induced recovery rate of MB patients
with respect to the treatment induced recovery rate of MB patients  and also differentiate
and also differentiate  with respect to the recovery rate of PB patients
with respect to the recovery rate of PB patients . This gives
. This gives

and
 .
.
We can draw the conclusion that MDT chemotherapy has a positive impact on the control of leprosy.
• The rate of disease progression to the infectious classes ( and
and ) and probability of a successful interaction between a susceptible and an infectious individual, (
) and probability of a successful interaction between a susceptible and an infectious individual, ( and
and ) have the same effect on
) have the same effect on  for system (9) as in the analysis of
for system (9) as in the analysis of  for model system (1). The deductions and recommendations we made for system (1) still hold for the model with MDT treatment.
for model system (1). The deductions and recommendations we made for system (1) still hold for the model with MDT treatment.
• If we remove MDT terms from the expression for , i.e. if we let
, i.e. if we let  tend to zero and let
tend to zero and let  to be due to natural recoveries only, then
to be due to natural recoveries only, then  for system (9) tends to the reproduction rate for model system (1).
for system (9) tends to the reproduction rate for model system (1).
5. Model with Inadequate Treatment and Non-Compliance
We consider the situation in which leprosy patients have access to MDT chemotherapy. In the previous section, ideally, patients were adherent, and the treatment received was assumed adequate. We aim to model the situation in which some of the patients are non-compliant to treatment procedures, some altogether default and for some, the treatment received is inadequate. Treatment received is deemed inadequate when after completion of MDT, there is still bacilli present in the patient’s body, predisposing him/her to a relapse or for some other reason the disease re-manifests after treatment has been completed. We recall that if a patient defaults from treatment, a relapse is almost always imminent; the same applies to non-compliant patients, to a certain extent [14]. Also, when one begins MDT treatment, he/she ceases to be infectious, thus transmission is interrupted almost immediately. When the disease relapses, the patient eventually becomes infectious again. Our study in this section is based on the supposition that, at some point in the asymptomatic phase of the relapse, the patient must be able to communicate the infection.
5.1. Model Formulation
The model we propose introduces infectious carrier states for MB and PB patients in the asymptomatic phase of a relapse, i.e. before leprosy clinically re-manifests. The model classifies the population into seven time dependent classes: , and
, and ; which are still defined as per the last section.
; which are still defined as per the last section.
 —Infectious class of persons whose infection has progressed to multibacillary leprosy (MB),
—Infectious class of persons whose infection has progressed to multibacillary leprosy (MB),  —Infectious MB patients in the asymptomatic phase of a relapse,
—Infectious MB patients in the asymptomatic phase of a relapse, —Infectious class of persons whose infection has progressed to paucibacillary leprosy (PB),
—Infectious class of persons whose infection has progressed to paucibacillary leprosy (PB), —Infectious PB patients in the asymptomatic phase of a relapse.
—Infectious PB patients in the asymptomatic phase of a relapse.
Infection is transmitted to the susceptible persons through successful contacts with either a PB or MB patient. These patients must be in the asymptomatic phase of a relapse or whose initial infection or relapse has progressed to either clinical PB or MB. The force of infection can be expressed as

where

and
 .
.
 and
and  represent the probability of an MB or PB patient successfully infecting a susceptible during interaction, respectively.
represent the probability of an MB or PB patient successfully infecting a susceptible during interaction, respectively.
 are modification parameters which model the fact that individuals in the asymptomatic phase of a relapse are less infectious than those showing symptoms. MB patients, in
are modification parameters which model the fact that individuals in the asymptomatic phase of a relapse are less infectious than those showing symptoms. MB patients, in  either recover under treatment, pass away due to both natural and disease induced mortality or move into a carrier state,
either recover under treatment, pass away due to both natural and disease induced mortality or move into a carrier state,  before the remanifestation of MB leprosy. PB patients in the carrier state,
before the remanifestation of MB leprosy. PB patients in the carrier state,  progress to clinical PB.
progress to clinical PB.
• 5.1.1. Assumptions
• Patients in the asymptomatic phase of a relapse (or in the carrier state) are able to transmit the disease to susceptible individuals.
• Transmission is only through interactions between the susceptible person and either a PB or MB individual who is manifesting the disease or in the asymptomatic stage of a relapse.
• Transmission follows the mass action principle.
• PB leprosy in not fatal and its cases can recover naturally or due to the treatment.
• MB patients can recover under treatment; however they are still subject to mortality due to disease related complications.
• A portion of PB and MB patients who have had access to treatment experience a relapse.
• Patients who recover naturally or under treatment become non-infectious and are immune to re-infections.
From model (9), the assumption about the homogenous mixing of the population still holds. We also assume that no individual is naturally or artificially immune to the disease, immunity is only acquired through recovery from infection. Again, there is no migration; new recruits enter the population through birth and the population decreases by natural or disease induced mortality.
5.1.2. Parameters
 —rate at which MB patients who have accessed treatment move into the asymptomatic phase of a relapse.
—rate at which MB patients who have accessed treatment move into the asymptomatic phase of a relapse.
 —rate at which PB patients who have accessed treatment move into the asymptomatic phase of a relapse.
—rate at which PB patients who have accessed treatment move into the asymptomatic phase of a relapse.
 —rate at which patients in the asymptomatic phase of an MB relapse progress to clinical MB.
—rate at which patients in the asymptomatic phase of an MB relapse progress to clinical MB.
 —rate at which patients in the asymptomatic phase of a PB relapse progress to clinical PB.
—rate at which patients in the asymptomatic phase of a PB relapse progress to clinical PB.
For this model, we retain the rest of the parameters from the model (9) and maintain their definitions.
5.2. Model Equations
 (10)
(10)
Initial conditions for system (10) are

where  are all nonnegative.
are all nonnegative.
For model (10),

5.3. Effective Reproductive Number
The effective reproduction number is

We can express  as the sum of two quantities,
as the sum of two quantities,  where
where

and

 and
and  are the respective reproductive numbers for the multibacillary and for the paucibacillary forms of the disease.
are the respective reproductive numbers for the multibacillary and for the paucibacillary forms of the disease.
Analysis of 
From the analysis of , we can make a few general deductions and recommendations concerning transmission of leprosy with inadequate MDT treatment and noncompliance.
, we can make a few general deductions and recommendations concerning transmission of leprosy with inadequate MDT treatment and noncompliance.
1) To assess the effect of inadequate MDT treatment on transmission of leprosy, we first differentiate  with respect to
with respect to  the treatment induced progression rate of MB patients into the carrier state and then differentiate
the treatment induced progression rate of MB patients into the carrier state and then differentiate  with respect to
with respect to . This gives
. This gives


We can draw the conclusion that inadequate MDT chemotherapy has a negative impact on the control of leprosy. One way of ensuring that patients receive adequate treatment is to follow the recommendations of Hussain [2007][15] and administer MDT until smear negativity. The parameters under test also encapsulate non-compliance and defaulting. Patient follow ups and accompanied treatment administration have proved to be most effective against defaulting and non-compliance from experiences in other diseases (TB, for instance).
2) To assess the effect of adequate MDT treatment on transmission of leprosy, we first differentiate  with respect to the treatment induced recovery rate of MB patients
with respect to the treatment induced recovery rate of MB patients  and also differentiate
and also differentiate  with respect to the recovery rate of PB patients
with respect to the recovery rate of PB patients . This gives
. This gives

and

We can draw the expected conclusion that adequate MDT chemotherapy has a positive impact on the control of leprosy. Treatment is deemed adequate when no relapse has been experienced. The recommendations made above can ensure this.
3) The rate of disease progression to the infectious classes, ( and
and ) and probability of a successful interaction between a susceptible and an infectious individual, (
) and probability of a successful interaction between a susceptible and an infectious individual, ( and
and ), respectively, have the same effect on
), respectively, have the same effect on  for system (10) as in the analysis of
for system (10) as in the analysis of  and
and  for the prior model systems. The deductions and recommendations we made for systems (1) and (9) still hold for the model with inadequate MDT treatment.
for the prior model systems. The deductions and recommendations we made for systems (1) and (9) still hold for the model with inadequate MDT treatment.
4) If we let  and
and  tend to zero, i.e. if there is no progression into a relapse,
tend to zero, i.e. if there is no progression into a relapse,  tends to the reproduction rate for the model with adequate treatment and compliant patients.
tends to the reproduction rate for the model with adequate treatment and compliant patients.
6. Numerical Simulations
In this Section, we present numerical simulations of the three models discussed in the previous sections. We use the fourth order Runge-Kutta numerical scheme coded in Visual Basic for Applications and we also utilized Microsoft Excel. In our simulations we used parameter values estimated from the results of various literature and surveys done in Sub-Saharan African countries. Where relevant data was unavailable, we made do with statistics from Indian researches, which happen to be the most extensive. The progression rates to clinical infections were estimated from the average incubation periods of 5 and 10 years for PB and MB, which happen to be estimates themselves since there is no test for detecting sub-clinical infections. Throughout this exercise, we considered a hypothetical population of just below 1.1 million people. We derived the initial conditions of the infectious classes from the (worst case) prevalence rate of 10 per 1000 population [16,17] in areas still endemic for the disease in Sub-Saharan Africa. A study in Ethiopia found that 6% of the normal population incubates the disease [3]. We derived initial value for the latent infections from this observation. We first present simulations for the basic model to give us a portrait of the general behavior of Leprosy in a hypothetical population. We then go on to exhibit simulations for the model with adequate treatment and then finally for the one with inadequate treatment and non-compliance.
Numerical values of the parameters are as shown in the Table 1 below.
7. Discussion
In model (1), we presented a basic deterministic compartmental model for the transmission dynamics of leprosy in a community without access to treatment and with no other control measures in place (quarantines of lepromatus cases, as an example). Conditions for the stability of the disease-free equilibrium were established. It was shown that the disease-free equilibrium is locally asymptotically stable whenever the basic reproduction number is less than unity. We also showed that the endemic equilibrium can exist if the reproduction rate exceeds unity. Numerical results in Figure 2 show that the relative values of birth rate and mortality rate have a heavy bearing on the behavior of model system 1. It was shown through numerical simulation that without treatment, the disease eventually becomes highly endemic (Figure 3).
In model (9), we presented a deterministic compartmental model of leprosy in a community with access to MDT treatment. We assumed that treatment completely cured the patients who were themselves assumed to be compliant. Similar conditions for the stability and existence of the equilibrium states where established. Numerical simulations showed that the disease fails to establish itself in the presence of MDT treatment (Figure 4). This is consistent with the findings in references [16,18-21]. However, according to the simulations, the higher the level of treatment, the swifter the disease is eliminated from the community (Figure 5).
In model (10), we presented a theoretical deterministic compartmental model of leprosy in a community with
Table 1. Model parameters and their interpretations.

 (a)
(a) (b)
(b)
Figure 2. (a)Showing the general result if the parameter value for mortality rate is less than the birth rate; (b) Showing the general result if the parameter value for mortality rate exceeds the birth rate. We consider general cases for illustration.
 (a)
(a) (b)
(b)
Figure 3. (a) and (b) are graphs of numerical solutions showing the propagation of susceptible population and the infectious population respectively. Initial conditions: 
 (a)
(a) (b)
(b)
Figure 4. (a) and (b) are graphs of numerical solutions showing the propagation of susceptible population and the infectious population respectively. Initial conditions:  We consider general cases for illustration.
We consider general cases for illustration.

Figure 5. The graph shows the number of infectives plotted against time in years. The arrow shows the direction of increase of the level of treatment administered. The graphs where obtained for the following pairs of value for  and
and , respectively: (0.07, 0.875), (0.125, 0.175), (0.25, 0.35), and (0.376, 0.525) Initial conditions:
, respectively: (0.07, 0.875), (0.125, 0.175), (0.25, 0.35), and (0.376, 0.525) Initial conditions: 
 We consider general cases for illustration.
We consider general cases for illustration.
access to MDT treatment. We assumed that treatment fails to completely cure the patients, some of whom default or are not compliant with treatment procedures. Similar conditions for the stability and existence of the equilibrium states where established. Numerical simulations showed that the disease fails to establish itself in the presence of MDT treatment, despite the presence of cases of inadequate treatment and non-compliant behavior (Figure 6). This is consistent with the findings in reference [13]. Our simulations, however, show that leprosy is eliminated faster if patients are more adherent to treatment procedure and if the treatments completely cure the patient. Results in Figure 7 show that the infectious population gradually completely decays to zero but the decay rate of progression into a relapse is greater.
We calculated the basic reproduction rate for all three models. Analysis for the basic model showed that increase in probability of successful infection during an interaction directly increased transmission as does the increase in rates of progression to clinical infections. Under application of MDT, adequate treatment directly decreased transmission. If there in non-compliant behavior or if treatment is proving inadequate, such a trend tends to increase the reproduction rate of the disease.
We tried to relate this study to the particular case of Sub-Saharan Africa in the model formulation and estimation of the parameter values and initial points for the simulations. As such, our models depict the transmission
 (a)
(a) (b)
(b)
Figure 6. (a) and (b) are graphs of numerical solutions showing the propagation of susceptible population and the infectious population respectively. Initial conditions:  We consider general cases for illustration.
We consider general cases for illustration.

Figure 7. The arrow shows the direction of increase of the level of the rate of progression into relapse. The graphs where obtained for the following pairs of value for  and
and  respectively: (0.01, 0.02), (0.02, 0.04), (0.04, 0.08) and (0.08, 0.16). Initial conditions: S0 = 1,000,000, E0 = 59,000, M1,0 = 5000, M2,0 = 500, P1,0 = 5000, P2,0 = 500,. We consider general cases for illustration.
respectively: (0.01, 0.02), (0.02, 0.04), (0.04, 0.08) and (0.08, 0.16). Initial conditions: S0 = 1,000,000, E0 = 59,000, M1,0 = 5000, M2,0 = 500, P1,0 = 5000, P2,0 = 500,. We consider general cases for illustration.
of leprosy in the region. We can therefore present the result that without treatment or control, leprosy settles into a rather high endemicity in the Sub-Saharan Africa (SSA) region. Multi-Drug Therapy (MDT) polychemotherapy can prevent the disease from establishing itself by impelling the disease into a disease free state. Since the introduction of MDT such a trend (falling prevalent rates) has been observed on a global scale. We can also emphasize that the higher the level of treatment availed to the population, the faster, leprosy is eliminated. If there in non-compliant behavior, defaulting or if treatment is proving inadequate (i.e. if there are relapses), the disease again fails to establish itself, but the return to a disease free state will be slower depending on the extent to which the treatment is proving inadequate for the SSA population.
REFERENCES
- World Health Organization (WHO), “Fact Sheet on Leprosy,” 2009. www.who.int
- “Definitions and Technical Guidelines for Leprosy Case Holding in the Frame of the Leprosy Elimination Strategy,” Regional Leprosy Elimination Programme, Regional Office for Africa Division of Prevention and Control of Communicable Diseases, 2002.
- “Principles of Medicine in Africa (P575-P590),” Cambridge University Press, Cambridge, 3rd Edition, 2004.
- “Oxford Handbook of Tropical Medicine,” Oxford University Press, Oxford, 3rd Edition, 2008.
- Centre for Disease Control (CDC), “Leprosy: Technical Information,” 2009. www.cdc.gov
- P. van den Driessche and J. Watmough, “Reproduction Numbers and Sub-Threshold Endemic Equilibrium for Compartmental Models of Disease Transmission,” Mathematical Biosciences, Vol. 180, No. 1-2, 2002, pp. 29- 48. doi:10.1016/S0025-5564(02)00108-6
- C. Castillo-Chavez, Z. Feng and W. Huang, “On the Computation of
 and Its Role in Global Stability. Mathematical Approaches for Emerging and Reemerging Infectious Diseases: An Introduction,” The IMA Volumes in Mathematics and Its Applications, Vol. 125, 2002, pp. 229-250.
and Its Role in Global Stability. Mathematical Approaches for Emerging and Reemerging Infectious Diseases: An Introduction,” The IMA Volumes in Mathematics and Its Applications, Vol. 125, 2002, pp. 229-250. - J. Watmough, “Computation of the Basic Reproduction Number,” MITACS-PIMS Summer School on Mathematical Modelling of Infectious Disease, University of Alberta, Edmonton, 2008.
- C. Castillo-Chavez and B. Song, “Dynamical Models of Tuberculosis and Their Applications,” Mathematical Biosciences and Engineering, Vol. 1, No. 2, 2004, pp. 361- 404. doi:10.3934/mbe.2004.1.361
- J. Carr, “Applications Centre Manifold Theory,” SpringerVelag, New York, 1981. doi:10.1007/978-1-4612-5929-9
- A. Meima, M. D. Gupte, G. J. van Oortmarssen and J. D. Habbema, “SIMLEP: A Simulation Model for Leprosy Transmission and Control,” International Journal of Leprosy and Other Mycobacterial Diseases, Vol. 67, No. 3, 1999, pp. 215-236.
- C. Bandit, “Recent Advances in Leprosy Chemotherapy,” Journal of Tropical Medicine & Parasitology, Vol. 29, No. 2, 2006, pp. 68-76.
- B. K. Girdhar and D. A. Girdhar, “Short Course Treatment of Leprosy,” Central JALMA Institute for Leprosy, Present Status, 2002.
- S. R. Pattyn, J. A. Husser, L. Janssens, S. Grillone and J. Bourland, “Inadequate Treatment in Multibacillary Leprody and Incubation Times for Relapses,” Acta Leprologica, Vol. 4, No. 4, 1986, pp. 495-499.
- T. Hussain, “Leprosy Patients Attending the Out Patient’s Clinic at Agra: A Retrospective Analysis of the Characteristics and Frequency of Regularity VS Irregularity for Determining Absenteeism, Non-Adherence and NonCompliance Division of Biostatistics,” National JALMA Institute for Leprosy and Other Mycobacterial Diseases, 2007.
- J. D. Habbema, “Trends in Leprosy Case Detection Worldwide since 1985,” University Medical Center Rotterdam, Erasmus, 2004.
- B. R. Bloom and T. Godal, “Selective Primary Health Care: Strategies for Control of Disease in the Developing World,” V. Leprosy, Vol. 5, No. 4, 1983, pp. 765-780.
- J. H. Richardus and J. D. F. Habbema, “The Impact of Leprosy Control on the Transmission of M. leprae: Is Elimination Being Attained?” Leprosy Review, Vol. 78, No. 4, 2007, pp. 330-337.
- M. F. Lechat, C. B. Misson, M. Vanderveken, C. M. Vellut and E. E. Declercq, “A Computer Simulation of the Effect of MDT on the Incidence of Leprosy,” Annales de la Societe Belge de Medecine Tropicale, Vol. 67, 1987, pp. 59-65.
- A. Meima, L. M. Irgens, G. J. van Oortmarssen, J. H. Richardusa and J. D. Habbema, “Disappearance of Leprosy from Norway: An Exploration of Critical Factors Using Anepidemiological Modelling Approach,” International Journal of Epidemiology, Vol. 31, No. 5, 2002, pp. 991-1000. doi:10.1093/ije/31.5.991
- A. Meima, W. Cairns, S. Smith, G. J. van Oortmarssen, J. H. Richardus and J. D. F. Habbema, “The Future Incidence of Leprosy: A Scenario Analysis,” Bulletin of the World Health Organization, Vol. 82, No. 5, 2004, pp. 373-385.

