Applied Mathematics
Vol.3 No.10A(2012), Article ID:24121,8 pages DOI:10.4236/am.2012.330195
Optimal Policies for Managing Invasive Species under Uncertainty
1Economic Research Service, United States Department of Agriculture, Washington DC, USA
2Office of Chief Economist, United States Department of Agriculture, Washington DC, USA
Email: *ckim@ers.usda.gov, MAillery@ers.usda.gov, jlewandrowski@oce.usda.gov, sgkimwin@knu.ac.kr
Received July 6, 2012; revised August 9, 2012; accepted August 16, 2012
Keywords: Invasive Species; Preventive Measures; Control Measures; Induced Technology; Hazard Function; Optimal Control Model
ABSTRACT
We present an optimal control model of three stages of resources allocation for managing invasive species. Three types of temporal uncertainty are considered, involving the timing of discovery of an invasive pest, the timing of an induced technology development after the establishment and dispersion of an invasive species, and the timing of farmer adoption of induced technology as the costs of controlling the invasive species increase. Using a bioeconomic optimal control model of managing invasive species, where models in previous studies are subset within our model, we show that when sub-structured models not including all three stages are used for managing invasive species, resource allocation for adopting preventive measures before the initial discovery of an invasive pest would be supra-optimal while resource allocation for adopting conventional control measures after establishment and dispersion would be sub-optimal.
1. Introduction
Public policy for managing invasive species has largely focused on preventive measures during the period prior to detection (stage 1) and on control measures after the establishment and dispersion of the invasive species (stage 2). Results from previous studies suggest that more resources should be allocated to fund prevention measures implemented before establishment of an invasive species than to fund control measures after an invasive species establishment [1,2]. After establishment and dispersion of the invasive species in stage 2, however, Kotani et al. [3] suggested that optimal policy depends not only on the initial stock of the invasive species, but also on the sensitivity of management cost increases that occur in response to a change in the stock over time. Their results suggest that any type of eradication policy is unlikely to be optimal if the sensitivity of cost increases for invasive species management is high.
While manageability of economic and ecological damages due to invasive species depends largely on available control technologies, little attention has been paid to the effect of induced technical change and farmer adoption of new control technologies on the resource allocation for adopting conventional control measures [4]. As the costs of control drastically increase during the initial establishment and dispersion phase, new technologies can be developed in stage 2, and then adopted in response to an increase in management costs in stage 3. Bt (Bacillus thuringiensis) corn and Bt cotton represent examples of an adaptive response to infestation of an invasive species. Another example is the Sterile Insect Technique, which was developed and improved in response to costly introductions of the New World Screwworm and the Mediterranean fruit fly into the United States. In stage 3, however, some farmers may employ conventional control measures to mitigate the invasive species infestation, while other farmers may adopt the newly developed technology. Failure to consider induced technology in stage 2 and its adoption in stage 3 can lead not only to inefficient resource allocation for controlling invasive species during management stage 2 [4], but also to counterproductive policy recommendations [5].
Optimal policy recommendations in managing invasive species have been based on sub-structured models; either stage 2 only [6], or both stages 1 and 2 [1,2,7,8], or both stages 2 and 3 [4,8]. However, to our knowledge, a fully structured model covering all three stages of managing invasive species has not been presented in the literature. When policy recommendations are made with sub-structured bio-economic dynamic models, we show that resource allocation for adopting preventive measures before the initial discovery of an invasive pest (i.e., stage 1) would be supra-optimal while a resource allocation for adopting conventional control measures following the discovery in stage 2 would be sub-optimal.
To examine this issue, we extend the recent work by Kim et al. [4] addressing management of invasive species in the presence of endogenous technological change with uncertainty by incorporating preventive measures before the discovery of an invasive species [1]. Technical change we focus on is often the outcome of joint research across government, academic and corporate enterprises, aimed at the development of a pest-induced technology innovation typically associated with a factor of production such as genetically engineered “Roundup Ready” seeds currently available for corn, soybean, cotton, and other crops.
The remainder of our paper is organized as follows. In Section 2, we present three types of temporal uncertainty associated with invasive species management and control practices: The timing of discovery of an invasive pest (stage 1); the timing associated with induced technology development after establishment and dispersion (stage 2); and the timing associated with farmer adoption of the induced technology as the costs of controlling the invasive species increase after establishment and dispersion (stage 3). In Section 3, we present a bioeconomic dynamic model to determine the optimal allocation of management resources. The model incorporates three risk components, as well as a logistic growth function of an invasive pest infestation, within a nested optimal control model of managing invasive species to broadly examine optimal resource allocation policies for managing an invasive species across stages 1 through 3. Economic properties of the optimal solutions for invasive species management are discussed. Section 4 provides concluding remarks.
2. Risks Associated with Invasive Species Management
Hazard-function methods have been employed within dynamic economic frameworks under uncertainties where temporal considerations matter [9], as in the case of the uncertain entry time of firms within an industry [10], the uncertain discovery time of an invasive species [1], the uncertain timing of an innovation from public/private research investments [4,9], and uncertainty in the timing of adoption of a new technology [4,11]. Uncertainties enter our economic model with respect to the timing of the discovery of an invasive pest, the development of an induced technology designed to reduce management costs, and adoption of an induced technology by producers.
We first define F(t) to be the probability that discovery of an invasive pest has occurred by time t, with F (t = 0) = 0, as follows:
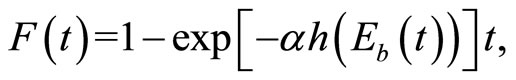 (1)
(1)
where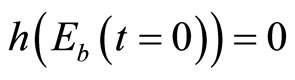 ,
, 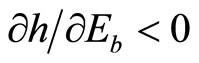 ,
, 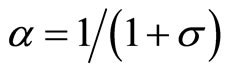 , and Eb(t) represents preventive measures adopted before the initial discovery of the invasive species such that
, and Eb(t) represents preventive measures adopted before the initial discovery of the invasive species such that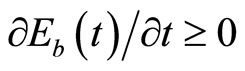 ,
, 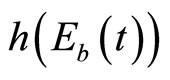 is the hazard rate representing the conditional probability that discovery will occur during the next time unit,
is the hazard rate representing the conditional probability that discovery will occur during the next time unit, 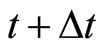 , given that discovery has not occurred at time t, and
, given that discovery has not occurred at time t, and 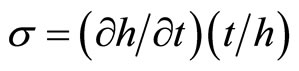 is the time elasticity of the conditional probability of preventive measures. For an optimal control model of invasive species management, Equation (1) can be rewritten as the following state equation1:
is the time elasticity of the conditional probability of preventive measures. For an optimal control model of invasive species management, Equation (1) can be rewritten as the following state equation1:
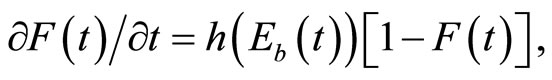 (2)
(2)
where 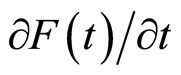 is the probability density function for the time of first discovery of the invasive species.
is the probability density function for the time of first discovery of the invasive species.
Once an invasive species has arrived and is established, and costs for managing and controlling the infestation increase, we consider the case of a representative producer adopting an induced technology that mitigates control costs. To make the timing of developing a new technical innovation in the future endogenous, we also employ a hazard-function approach where the probability of a new technical innovation occurring is influenced by the increasing costs of control. Corporate enterprises (and government) are assumed to respond to potential farmlevel damages from an invasive species as an indication of farmers’ (and society’s) willingness to pay to avoid damages associated with invasive species infestations [4]. That is, the extent to which technical innovation is an increasing function of the cost of invasive-species management depends on farmers’, as well as society’s, desire to combat increasing management costs. In the absence of technical innovation, control costs and damages resulting from an invasive species infestation are assumed to increase.
The probability of developing a technical innovation at any time γ, where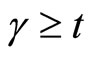 , given that an innovative technology has not been developed yet, is modeled as an increasing function of the cost of control. First, we let M(γ) be the probability associated with the development of a technical innovation occurring by time γ, where
, given that an innovative technology has not been developed yet, is modeled as an increasing function of the cost of control. First, we let M(γ) be the probability associated with the development of a technical innovation occurring by time γ, where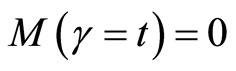 . The conditional probability of developing a technical innovation at time γ,
. The conditional probability of developing a technical innovation at time γ, 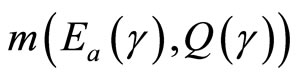 , is the probability that the development of such an innovation will occur during the next time period,
, is the probability that the development of such an innovation will occur during the next time period, 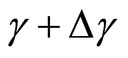 , given that a new technology has not been developed at time γ, where
, given that a new technology has not been developed at time γ, where 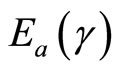 represents chemical/mechanical control measures and
represents chemical/mechanical control measures and 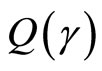 represents biological control measures, both to be considered, after an invasive species’ establishment.
represents biological control measures, both to be considered, after an invasive species’ establishment.
The likelihood of developing a new technology is expressed as follows:
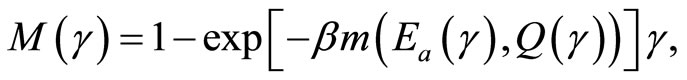 (3)
(3)
where
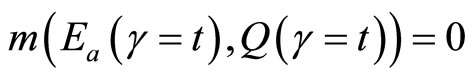 ,
, 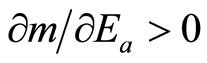 ,
, 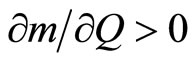 , and
, and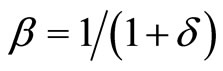
and 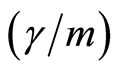
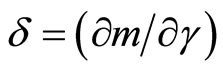
is the time elasticity of the conditional probability of developing a technical innovation.
Equation (3) can be rewritten as a state equation within an optimal control model as follows:
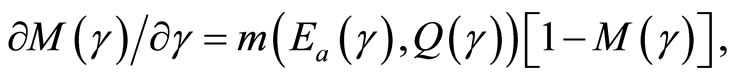 (4)
(4)
where 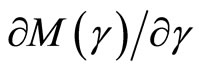 is the probability density function for the time the induced innovation occurs.
is the probability density function for the time the induced innovation occurs.
Once a technical innovation occurs at time γ, economic benefits associated with the management of an invasive species depend largely on whether the innovative technology is adopted. Therefore, we let N(τ) be the probability of adoption of a technical innovation developed at time 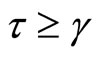 where
where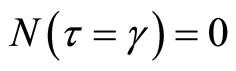 . Then, the conditional probability of adopting a new technology at time τ,
. Then, the conditional probability of adopting a new technology at time τ, 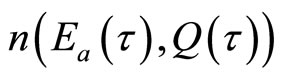 , is the probability that adoption of such an innovation will occur during the next time period, τ + Δτ, given that such an innovation has not been adopted at time τ. The likelihood of adoption is expressed as follows:
, is the probability that adoption of such an innovation will occur during the next time period, τ + Δτ, given that such an innovation has not been adopted at time τ. The likelihood of adoption is expressed as follows:
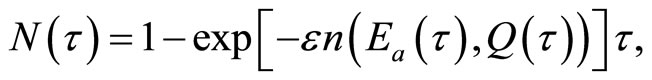 (5)
(5)
where
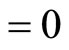
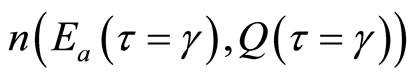 ,
,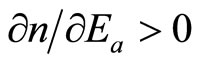 ,
, 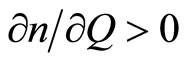 ,
,
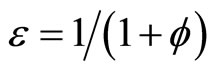 and
and 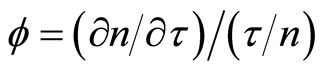
is the time elasticity of the conditional probability of developing a technical innovation. Equation (5) can also be rewritten as a state equation within our optimal control model as follows:
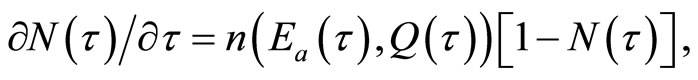 (6)
(6)
where 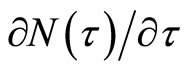 is the probability density function for the time of adopting the induced technology. The three state Equations (2), (4), and (6) associated with the timing of discovering an invasive species, the timing of developing an induced technology, and the timing of adoption, respectively, are incorporated into our optimal control model of managing invasive species in the following section.
is the probability density function for the time of adopting the induced technology. The three state Equations (2), (4), and (6) associated with the timing of discovering an invasive species, the timing of developing an induced technology, and the timing of adoption, respectively, are incorporated into our optimal control model of managing invasive species in the following section.
3. The Model
We use a logistic growth function to characterize the evolution of the pest population after introduction and establishment. For the case where a fraction of the stock of an invasive species is removed by use of conventional control measures, the rate of change in the invasive species stock is represented as follows [6]:
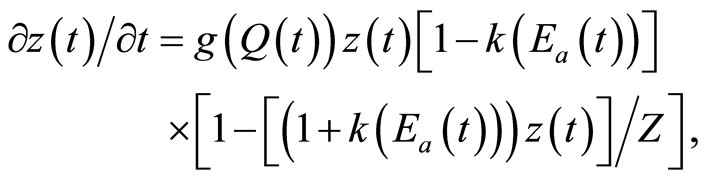 (7)
(7)
where z(t) is the stock of an invasive species in year t and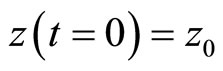 , g is the rate of intrinsic growth of the invasive species infestation, Q(t) represents the biological control measure in year t, with
, g is the rate of intrinsic growth of the invasive species infestation, Q(t) represents the biological control measure in year t, with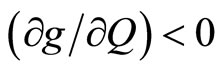 , and Z represents the maximum possible population of the invasive species, which depends on species characteristics as well as those of the infested environment. The parameter
, and Z represents the maximum possible population of the invasive species, which depends on species characteristics as well as those of the infested environment. The parameter 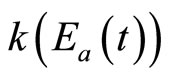 is a fractional coefficient
is a fractional coefficient 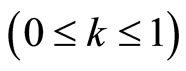 representing the population removal rate, and Ea(t) is assumed to represent the level of chemical and/or mechanical control measures implemented after the initial discovery of the invasive species, where
representing the population removal rate, and Ea(t) is assumed to represent the level of chemical and/or mechanical control measures implemented after the initial discovery of the invasive species, where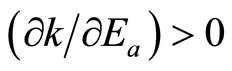 .
.
Subsequently, the value function associated with expected net social economic benefits under three types of risks is represented as follows:
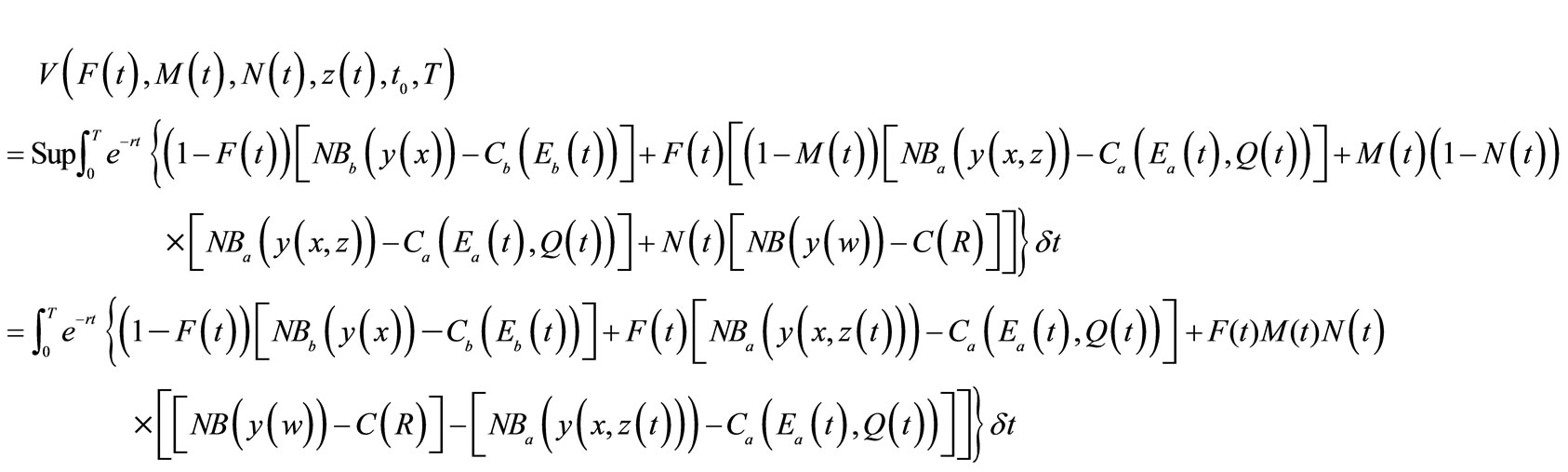 (8)
(8)
where T is the terminal time period, r is the rate of discount, NB represents net economic benefits of output (excluding the costs of managing the invasive species), and x and w identify conventional and induced technologies, respectively. The variable 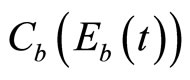 represents the costs associated with preventive measures, while
represents the costs associated with preventive measures, while 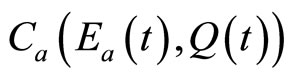 represents the costs to farmers of managing the invasive species with the implementation of chemical/mechanical pest control measures, as well as biological control measures, before the adoption of a new technology, and C(R) represents the investment costs for developing an innovative technology2. The net economic benefits resulting from the adoption of an induced technical innovation occurring,
represents the costs to farmers of managing the invasive species with the implementation of chemical/mechanical pest control measures, as well as biological control measures, before the adoption of a new technology, and C(R) represents the investment costs for developing an innovative technology2. The net economic benefits resulting from the adoption of an induced technical innovation occurring,  , are increasing over time as a function of the discounting of their costs, where y is output3. Therefore, the adoption of an induced technology requires that their net economic benefits,
, are increasing over time as a function of the discounting of their costs, where y is output3. Therefore, the adoption of an induced technology requires that their net economic benefits, 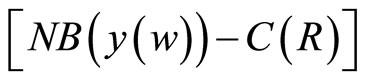 , be greater than or equal to the net economic benefits (less invasive species management costs) associated with the use of conventional technology in any given year,
, be greater than or equal to the net economic benefits (less invasive species management costs) associated with the use of conventional technology in any given year,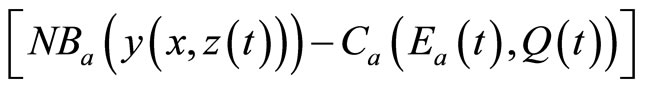 .
.
Equation (8) assumes that an induced technology (i.e., w) is developed with the probability of M(t), and that this new technology would be adopted by producers with the probability of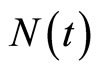 , while
, while 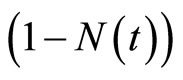 reflects the probability of producers employing the conventional technology. When F (t) = 1, our model is essentially identical with the model presented by Kim et al. [4], which considered the management and control of invasive species during stages 2 and 3. When M (t) = N (t) = 0, our model is identical with the models developed by Kim et al. [1] and Olson and Roy [2], which focused on stages 1 and 2 without the possibility of developing a new technology.
reflects the probability of producers employing the conventional technology. When F (t) = 1, our model is essentially identical with the model presented by Kim et al. [4], which considered the management and control of invasive species during stages 2 and 3. When M (t) = N (t) = 0, our model is identical with the models developed by Kim et al. [1] and Olson and Roy [2], which focused on stages 1 and 2 without the possibility of developing a new technology.
The Hamiltonian equation associated with objective function (8) and state Equations (2), (4), (6), and (7) (where the arguments of variables Eb, Ea and Q are hereafter omitted for convenience) is represented as follows:
where Eb, Ea, and Q are control variables, F, M, N, and z are state variables, and λ1 through λ4 are adjoint variables. The necessary conditions for optimality are represented in Appendix A4.
To interpret the economic properties of the optimal conditions presented in Equations (A1) through (A12), it is necessary to understand the adjoint variables λ1, λ2, λ3, and λ4. Following Arrow and Enthoven [12], Kamien and Schwartz [10], and Seierstad and Sydsæter [13], the adjoint variables λi (t0), where i = 1, 2, 3, 4 and 0 < t0 < T, approximate the marginal effects on the value function (shadow values) of the state variables, z, F, M, and N, respectively (Appendix B).
The adjoint variable λ1, which measures the marginal contribution (shadow value) of the state variable z (the invasive species stock) to the objective function value, is negative. Essentially, an increase in the invasive species population reduces the net economic benefits of management due to greater damages and management costs, but increases the probability of a new induced technology being developed and adopted. Furthermore, Equation (B1) indicates that the shadow value of λ1 would be overstated when the development of induced technology and its adoption by farmers are not considered in the model. Similarly, the adjoint variable λ2, which measures the marginal contribution of the state variable F (t) to the objective function value (i.e., the present value of the net social economic benefits) associated with an increase in the probability of discovering the invasive pest), is negative. Equation (B2) also indicates that the marginal net economic benefit (shadow value) of the probability of discovering invasive pests would be overstated when the development and adoption of induced technology are not considered.
Meanwhile, the adjoint variable λ4 in Equation (B4), which measures the marginal contribution of the state variable N(t) to the objective function value (shadow values) associated with an increase in the probability of adopting a new technology is positive. However, this result requires that the adjoint variable λ3 in Equation (B3), which measures the marginal contribution of the
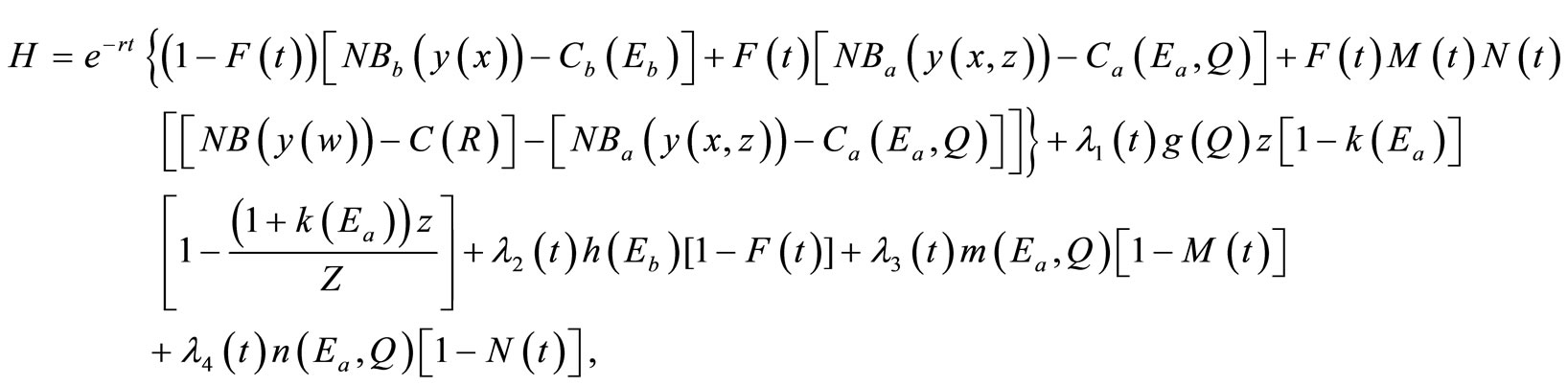 (9)
(9)
state variable M (t) to the objective function value (shadow values) associated with an increase in the probability of developing a new technology, becomes positive a short period following development and prior to adoption. But before interpreting these conditions, it is important to recognize that when an induced technology is developed, its marginal net economic benefit could initially be negative and then subsequently become positive. The eventual adoption of the induced technology requires that the associated net economic benefits over time, 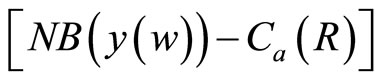 , be greater than those accruing to the conventional technology,
, be greater than those accruing to the conventional technology, 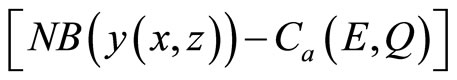 [4].
[4].
Equation (A1) states that before the initial discovery of an invasive species, the marginal costs of adopting preventive measures equal the marginal benefits (shadow values) resulting from a reduction of the hazard rate by adopting the preventive measures. However, the shadow values λ2 in Equation (B2) are overstated when an induced technology development and its adoption by farmers are not considered in the model; the marginal net economic benefits resulting from a reduction in the hazard rate due to adoption of preventive measures are overstated, leading to less investment for an induced technology development than is warranted. This result can be explained with Figure 1, where MB and MC represent the marginal benefits and marginal costs, respectively. The subscripts “b” and “a” represent before and after the initial discovery of the invasive species, respectively. The optimum level of adoption of preventive measures before the discovery of the invasive species is Eb, while it is at  when an induced technology development and its adoption by farmers are not considered in the model.
when an induced technology development and its adoption by farmers are not considered in the model.
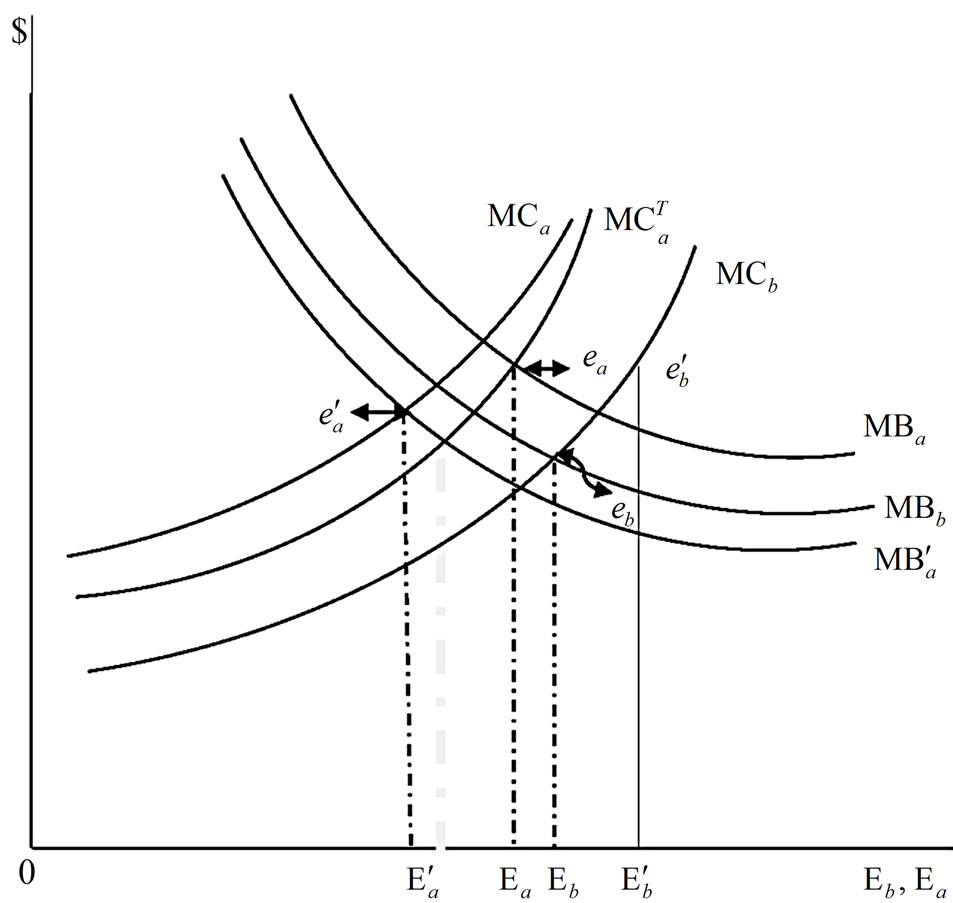
Figure 1. Effects of an induced technology on reource allocation for managing invasive species.
This result indicates that when an induced technology is not considered in the specification of a dynamic model for managing an invasive species infestation, the adoption of preventive measures before the discovery of invasive species would be more than adequate (supra-optimum).
Equation (A2) indicates that after the initial discovery of an invasive pest, the expected marginal costs of adopting chemical/mechanical control measures equal the sum of 1) The marginal benefits (shadow values) resulting from an increase in the removal rate of the invasive species population stock and 2) the economic benefits (shadow values) resulting from the development and adoption of an induced technology, which will occur because of increased costs of adopting chemical/mechanical control measures. An eqilibrium ea is attained in Figure 1, at the intersection of  and
and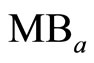 , where
, where  is the marginal costs associated with development and its adoption by farmers. When development and adoption of induced technology are not considered in the model, the marginal costs (i.e.,
is the marginal costs associated with development and its adoption by farmers. When development and adoption of induced technology are not considered in the model, the marginal costs (i.e.,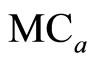 ) are overstated while the marginal benefits (i.e.,
) are overstated while the marginal benefits (i.e., ) associated with the adoption of chemical/mechanical control measures are understated. Therefore, the adoption of chemical/mechanical control measures prior to discovery of an invasive species,
) associated with the adoption of chemical/mechanical control measures are understated. Therefore, the adoption of chemical/mechanical control measures prior to discovery of an invasive species, 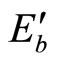 in Figure 1, is more than adequate (supra-optimum) while the adoption of control measures after the discovery of an invasive species,
in Figure 1, is more than adequate (supra-optimum) while the adoption of control measures after the discovery of an invasive species, 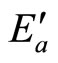 in Figure 1, would be less than adequate (sub-optimum).
in Figure 1, would be less than adequate (sub-optimum).
Equation (A3) states that after the discovery of an invasive pest, the expected marginal costs of adopting biological control measures equal the sum of the marginal benefits (shadow values) resulting from the reduction of the rate of intrinsic growth of the infestation and the economic benefits (shadow values) resulting from development and adoption of an induced technology, given increased costs of adopting biological control measures. These results also indicate that the adoption of biological control measures is less than adequate, as in the case of chemical/mechanical control measures (A2), when an induced technology development and adoption are not considered.
In summary, when induced technology is not considered as part of the analysis, the resources allocated for preventive measures before initial discovery of an invasive species would be more than adequate, while management resources allocated for control measures after the species discovery would be less than adequate.
4. Conclusions
This research extends previous work addressing the economics of invasive species management by covering three broad stages of management decision making, where the first stage considers adoption of preventive measures which occur before discovery of an invasive species; the second stage accounts for the adoption of conventional invasive-species management measures and the development of an induced technology; and the third stage represents the period when conventional control measures, as well as when an induced technology is developed and employed to reduce costs associated with management of the invasive species infestation.
Our results suggest that when a dynamic model designed to evaluate mitigating strategies for an invasive species infestation is specified without considering the development and adoption of induced technology, the recommended allocation of management resources resulting from that model would be counterproductive. First, our conceptual analysis reveals that, when induced technology is not considered, a management resource allocation for adopting preventive measures prior to the initial discovery of an invasive pest would be more than adequate. Second, the management resources allocated for adopting conventional species control measures after species discovery would be less than adequate. It should also be noted that the net economic benefits resulting from adoption of preventive measures before the discovery exceed those from conventional control measures implemented after the discovery, as demonstrated by Kim et al. [1] and Olson and Roy [2], regardless of whether the development and adoption of induced technology is considered.
The views expressed are those of the authors and should not be attributed to USDA.
REFERENCES
- C. S. Kim, R. N. Lubowski, J. Lewandrowski and M. E. Eiswerth, “Prevention or Control: Optimal Government Policies for Invasive Species Management,” Agricultural and Resource Economics Review, Vol. 35, No. 1, 2006, pp. 29-40.
- L. J. Olson and S. Roy, “On Prevention and Control of an Uncertain Biological Invasion,” Review of Agricultural Economics, Vol. 27, No. 3, 2005, pp. 491-497. doi:10.1111/j.1467-9353.2005.00249.x
- K. Kotani, M. Kakinaka and H. Matsuda, “Dynamic Economic Analysis on Invasive Species Management: Some Policy Implications of Catchability,” Mathematical Biosciences, Vol. 220, No. 1, 2009, pp. 1-14. doi:10.1016/j.mbs.2009.03.009
- C. S. Kim, G. D. Schaible, J. Lewandrowski and U. Vasavada, “Managing Invasive Species in the Presence of Endogenous Technological Change with Uncertainty,” Risk Analysis, Vol. 30, No. 2, 2010, pp. 250-260. doi:10.1111/j.1539-6924.2009.01312.x
- M. Grubb, J. Kőhler and D. Anderson, “Induced Technical Change in Energy and Environmental Modeling: Analytic Approaches and Policy Implications,” Annual Review of Energy and the Environment, Vol. 27, No. 1, 2002, pp. 271-308. doi:10.1146/annurev.energy.27.122001.083408
- C. S. Kim, D. Lee, G. Schaible and U. Vasavada, “Multiregional Invasive Species Management: Theory and an Application to Florida’s Exotic Plants,” Journal of Agricultural and Applied Economics, Vol. 39, Special Issue, 2007, pp. 111-124.
- M. E. Eiswerth and W. S. Johnson, “Managing Nonindigenous Invasive Species,” Environmental and Resource Economics, Vol. 23, No. 3, 2002, pp. 319-342. doi:10.1023/A:1021275607224
- B. Leung, D. M. Ludge, D. Finnoff, J. F. Shogren, M. A. Lewis and G. Lamberti, “An Ounce of Prevention or a Pound of Cure: Bioeconomic Risk Analysis of Invasive Species,” Royal Society, Vol. 269, No. 1508, 2002, pp. 2407-2413. doi:10.1098/rspb.2002.2179
- N. M. Kieffer, “Economic Duration Data and Hazard Functions,” Journal of Economic Literature, Vol. 26, No. 2, 1988, pp. 646-679.
- M. I. Kamien and N. L. Schwartz, “Limit Pricing and Uncertain Entry,” Econometrica, Vol. 39, No. 3, 1971, pp. 441-454. doi:10.2307/1913258
- N. L. Rose and P. L. Joskow, “The Diffusion of New Technologies: Evidence from the Electric Utility Industry,” Rand Journal of Economics, Vol. 21, No. 3, 1990, pp. 354-373. doi:10.2307/2555614
- K. J. Arrow and A. C. Enthoven, “Quasi-Concave Programming,” Econometrica, Vol. 29, No. 4, 1961, pp. 779- 800. doi:10.2307/1911819
- A. Seierstad and K. Sydsaeter, “Sufficient Conditions in Optimal Control Theory,” International Economic Review, Vol. 18, No. 2, 1977, pp. 367-391. doi:10.2307/2525753
- R. F. Stengel, “Optimal Control and Estimation,” 2nd Edition, Dover Publication Inc., New York, 1994.
Appendix A: Necessary Conditions for Optimality.
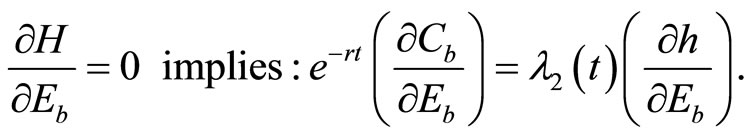 (A1)
(A1)
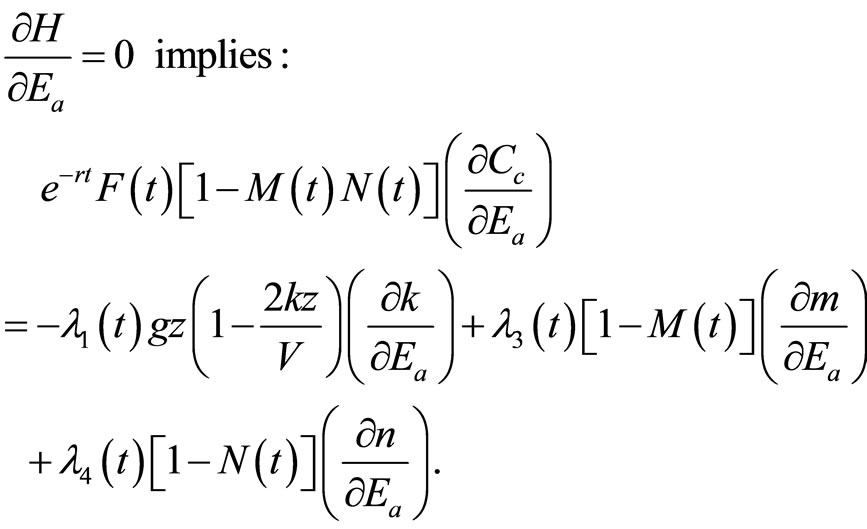 (A2)
(A2)
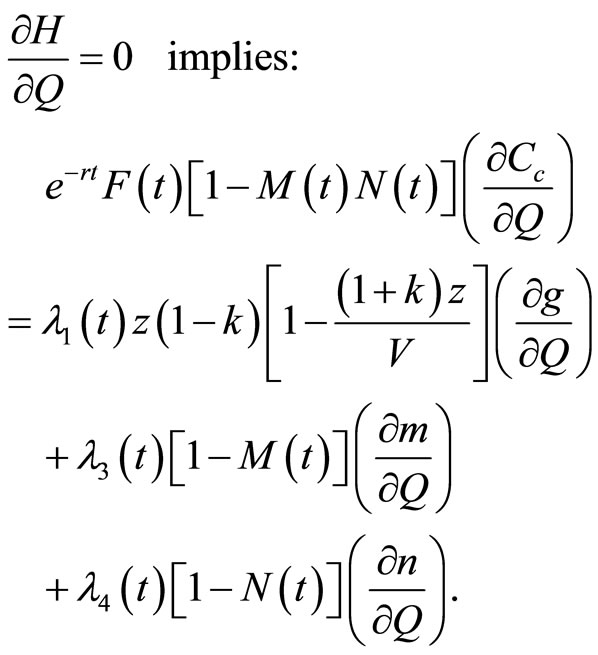 (A3)
(A3)
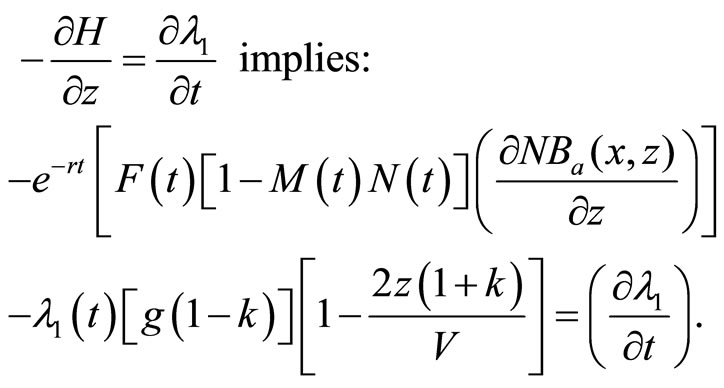 (A4)
(A4)
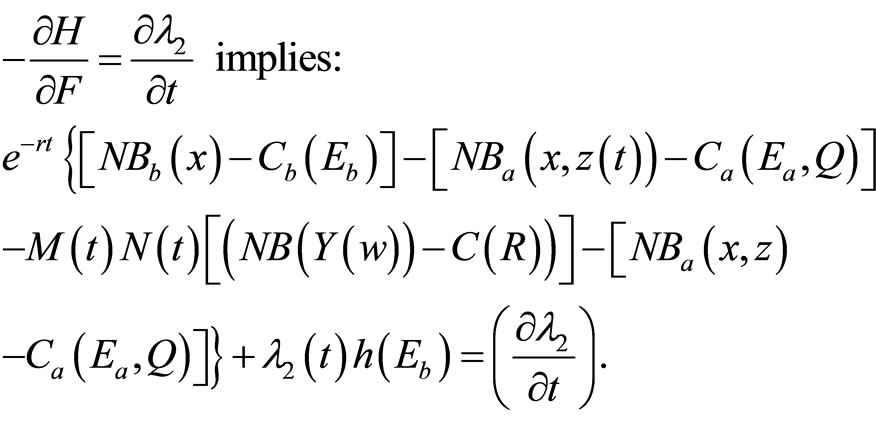 (A5)
(A5)
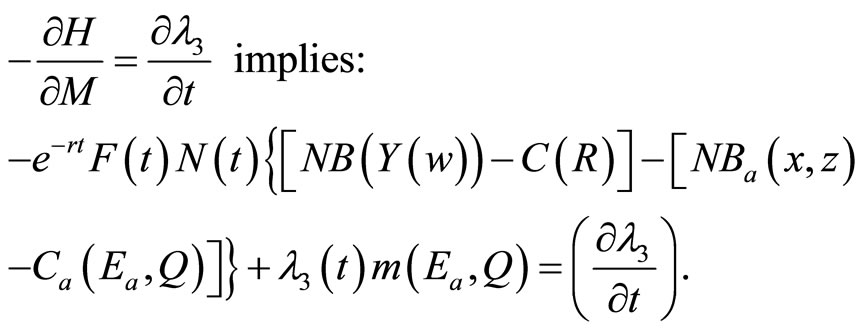 (A6)
(A6)
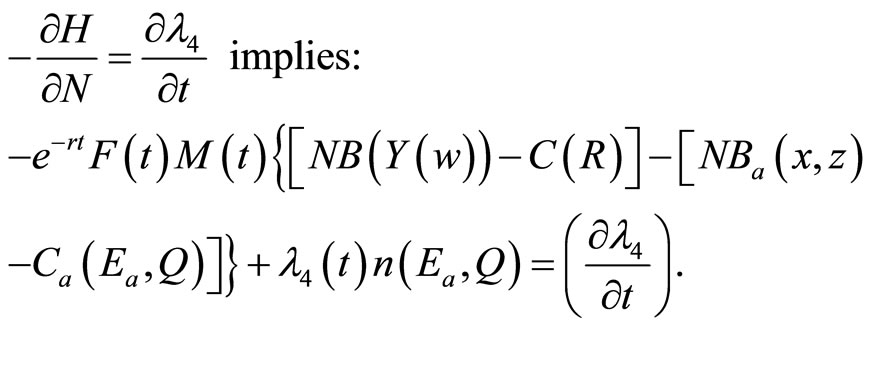 (A7)
(A7)
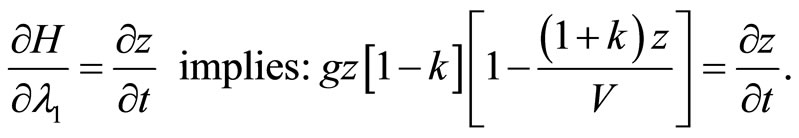 (A8)
(A8)
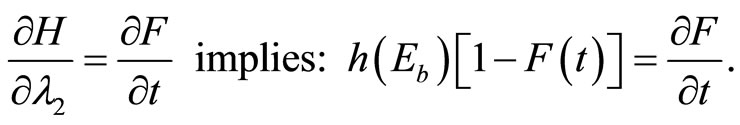 (A9)
(A9)
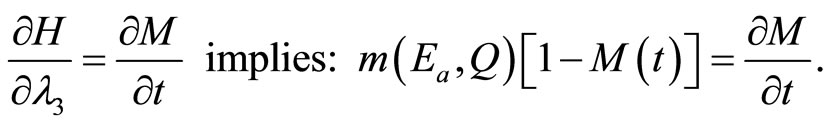 (A10)
(A10)
 (A11)
(A11)
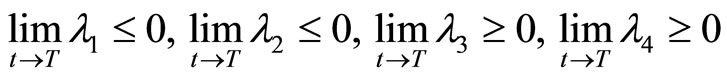 (A12)
(A12)
Appendix B: The Approximated Marginal Contribution of the State Variables at Time t0 to the Optimal Value Function
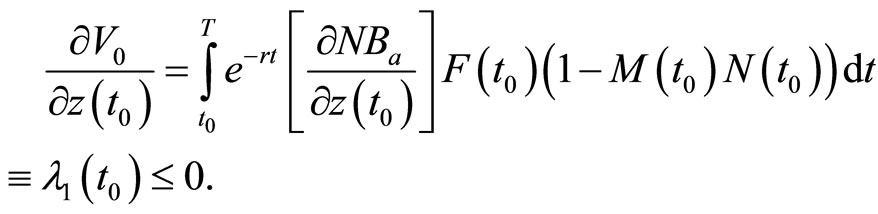 (B1)
(B1)
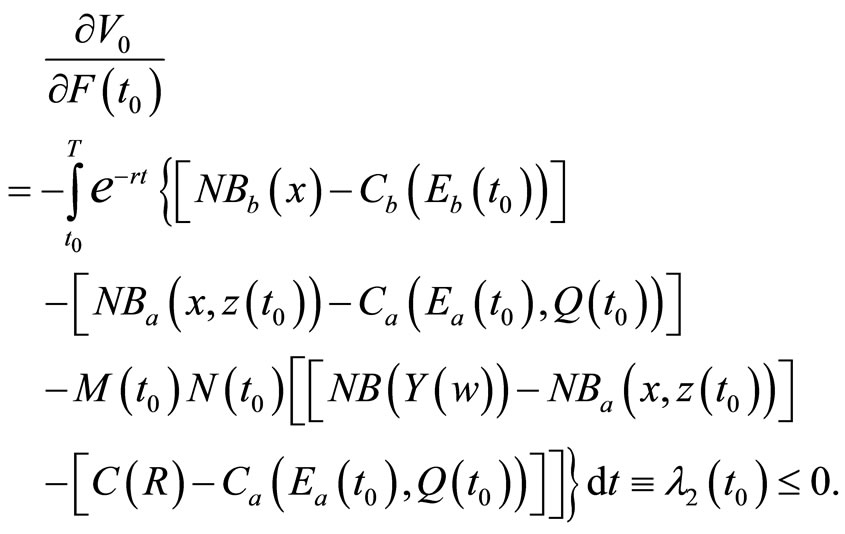 (B2)
(B2)
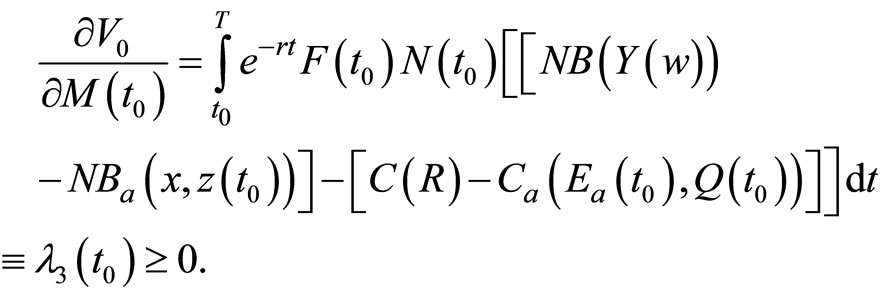 (B3)
(B3)
NOTES
*Corresponding author.
1Preventive (exclusionary) measures—such as trade restrictions, border inspections, and pest eradication programs in foreign countries—could be implemented after a species has been discovered, but they are generally less significant after discovery [1]. To simplify our model, preventive measures following discovery of an invasive pest are not considered in this article.
2For simplicity, investment costs for developing an innovative technology represent amortized values.
3Long-term costs to farmers, who choose to adopt a seed-based induced technology, by continually paying the rights to use the seed and forfeiting rights to produce their own seed, are incorporated into the net economic benefits associated with adoption of the induced technology, NB (Y (w)), See [4].
4The optimal solutions satisfying the necessary conditions presented in Equation (A1) through (A12) must also satisfy sufficient conditions. We assume Stengel’s [14] weaker version of sufficient conditions to assure optimality. For further discussion, see [4].

