Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 19997 , 5 pages DOI:10.4236/am.2012.37119
The Existence and Uniqueness of Random Solution to Itô Stochastic Integral Equation
School of Mathematics and Information Science, Northwest Normal University, Lanzhou, China
Email: hamdin@126.com
Received May 8, 2012; revised June 8, 2012; accepted June 15, 2012
Keywords: Itô Integral; Brownian Motion; Probabilistic Functional Analysis; Banach Space
ABSTRACT
The objective of this paper is to attempt to apply the theoretical techniques of probabilistic functional analysis to answer the question of existence and Uniqueness of a Random Solution to Itô Stochastic Integral Equation. Another type of stochastic integral equation which has been of considerable importance to applied mathematicians and engineers is that involving the Itô or Itô-Doob form of stochastic integrals.
1. Introduction
We shall give some historical remarks concerning the development of this type of equation and point out the essential difference between them and other random integral equations.
In 1930 N. Wiener introduced an integral of the form 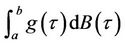 where
where  a deterministic real-valued function and
a deterministic real-valued function and  is a scalar Brownian motion process.
is a scalar Brownian motion process.
Author of [1] in 1944 generalized Wiener’s integral to include those cases where the integrand is random. That is he obtained an integral of the form
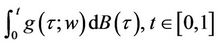
Which is referred to as the Itô stochastic integral or simply the stochastic integral. Since that time many scientists have contributed to the general development of this type of stochastic integral. For example see [2- 10].
In 1946 Author of [5] formulated a stochastic integral equation of the form
 (1.0)
(1.0)
where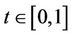 ,
,  is a scalar Brownian motion process, and C is a constant Restrictions are usually placed on the functions f and g so that the first integral is interpreted as the usual Lebesgue integral of the sample functions which can then be related to the sample integral of the process
is a scalar Brownian motion process, and C is a constant Restrictions are usually placed on the functions f and g so that the first integral is interpreted as the usual Lebesgue integral of the sample functions which can then be related to the sample integral of the process 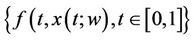 and the second integral is an Itô stochastic integral.
and the second integral is an Itô stochastic integral.
The principal feature which distinguishes the type of equation studied from an equation of the Itô type is the fact that in the former case each of the integrals involved is interpreted as a Lebesgue integral for almost all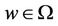 . That is, almost all sample functions are Lebesgue integrable. Since in the Itô stochastic integral the limit is taken in the mean-square or in the probability sense, the theory of such integrals has been developed as self-contained and self-consistent.
. That is, almost all sample functions are Lebesgue integrable. Since in the Itô stochastic integral the limit is taken in the mean-square or in the probability sense, the theory of such integrals has been developed as self-contained and self-consistent.
One of the main purposes of subsequent work in connection with the Itô stochastic integral equation has been to construct Markov processes such that their transition probabilities satisfy given Kolmogorov equations and to investigate the continuity of the processes, among other properties of the sample function.
The method of successive approximation was used by Itô and Doob to show the existence and uniqueness of a random solution to Equation (1.0).
2. Preliminaries
Let  be a scalar Brownian motion process. In this section we shall be concerned with the integral
be a scalar Brownian motion process. In this section we shall be concerned with the integral
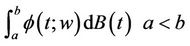 (1.1)
(1.1)
for a fairly general class of functions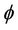 . This integral will be called the Itô stochastic integral as we mentioned previously. As is well known, almost all the sample functions of the Brownian motion process are of unbounded variation and hence the integral (1.1) cannot be defined as an ordinary Stieltjes integral.
. This integral will be called the Itô stochastic integral as we mentioned previously. As is well known, almost all the sample functions of the Brownian motion process are of unbounded variation and hence the integral (1.1) cannot be defined as an ordinary Stieltjes integral.
First we shall define the integral (1.1) for the class of step functions. That is, functions 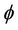 of the form
of the form
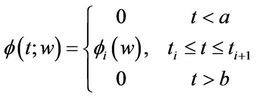 (1.2)
(1.2)
where 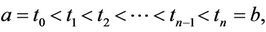
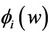 are measurable with respect to the
are measurable with respect to the 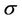 -algebra
-algebra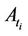 , and
, and
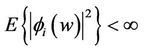 for such functions we define the Itô integral by
for such functions we define the Itô integral by
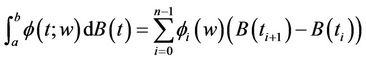 (1.3)
(1.3)
Now suppose that 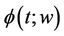 is any function satisfying the following conditions.
is any function satisfying the following conditions.
1) 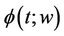 is a product-measurable function from
is a product-measurable function from , assuming the usual Lebesgue measure on
, assuming the usual Lebesgue measure on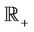 .
.
2) For each, 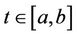 ,
, 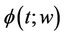 is measurable with respect to
is measurable with respect to 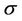 -algebra
-algebra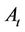 , where
, where 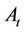 is the smallest
is the smallest 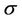 -algebra on
-algebra on , such that
, such that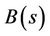 ,
,  is measurable.
is measurable.
3) 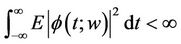
In view of Equation (1.2) it is evident that the class of step functions satisfy conditions 1)-3).
For the function 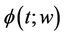 satisfying conditions 1)-3) we shall define their norm as follows:
satisfying conditions 1)-3) we shall define their norm as follows:
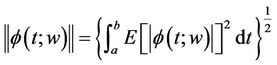 (1.4)
(1.4)
For this case author of [2] has shown the following 1)  can be approximated in the mean-square sense by a sequence of step functions
can be approximated in the mean-square sense by a sequence of step functions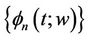 . That is
. That is
 as
as 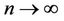
2) The sequence of integrals
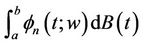
Possesses a mean-square limit. That is there exists a 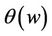 such that
such that
 (1.5)
(1.5)
as 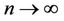
Now we shall define the integral (1.1) for a class of functions  satisfying conditions 1)-3) by
satisfying conditions 1)-3) by
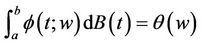 (1.6)
(1.6)
As with the ordinary integrals, we shall define
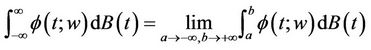 (1.7)
(1.7)
Definition 1.1 Let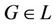 , where L denote the collection of Lebesgue measurable subsets of
, where L denote the collection of Lebesgue measurable subsets of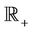 . Define a function
. Define a function 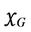 from
from 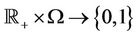 by
by
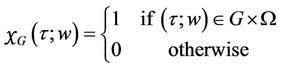
Lemma 1.1 The function 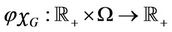 defined by
defined by

where  satisfies conditions 1)-3), and
satisfies conditions 1)-3), and 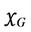 is as defined earlier, also satisfies conditions 1)-3).
is as defined earlier, also satisfies conditions 1)-3).
Proof. The proof is a straightforward result of the definition of 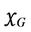 and the fact that
and the fact that 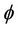 satisfies conditions 1)-3).
satisfies conditions 1)-3).
We are now in a position to define exactly what is meant by the expression
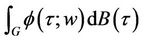
Definition 1.2 We define 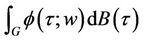 for G a Lebesgue-measurable subset of
for G a Lebesgue-measurable subset of 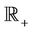 by
by
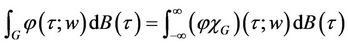
Note that lemma 1.4 guarantees the expression on the right exists and is well defined Definition 1.3 We shall denote by
 the space of all continuous functions from
the space of all continuous functions from 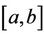 into
into . We shall define the norm of
. We shall define the norm of  by
by

Lemma 1.2

Lemma 1.3
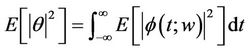
Lemma 1.4 If we define a distance between two functions 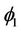 and
and 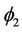 each satisfying conditions 1)-3) by
each satisfying conditions 1)-3) by
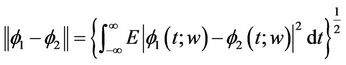
and the distance between 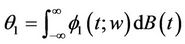 and
and 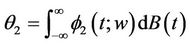 by
by
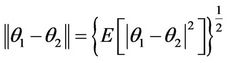
Then .
.
For the proof of the Lemmas see [2].
Lemma 1.5 Let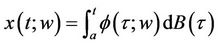 ,
, 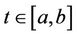
Then 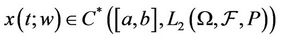
For the proof see [4].
3. On an Itô Stochastic Integral Equation
In this section we shall investigate a stochastic integral equation of the type
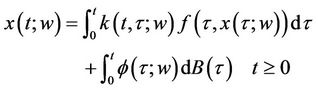 (2.1)
(2.1)
where  is the unknown random process defined for
is the unknown random process defined for 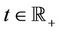 and
and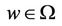 .
.
We shall place the following restrictions on the random functions which constitute the stochastic integral Equation (2.1).
1') 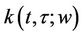 is an element of
is an element of 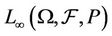 and
and  is continuous where
is continuous where  .
.
2') 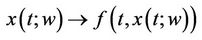 is an operator on the set S with values in the Banach space B satisfying
is an operator on the set S with values in the Banach space B satisfying
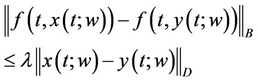
for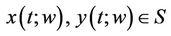 .
.
3') Conditions 1)-3) of section 1 hold.
Thus with the given assumptions the first integral of (2.1) can be interpreted as a Lebesgue integral and the second as an Itô stochastic integral.
We shall now proceed to state and prove a theorem concerning the behavior of the Itô integral. More precisely, if we show that the Itô integral is an element of the space , we can apply the theory of admissibility to Equation (2.1) to show the existence of a random solution. By a random solution to Equation (2.1) we mean a random function
, we can apply the theory of admissibility to Equation (2.1) to show the existence of a random solution. By a random solution to Equation (2.1) we mean a random function  from
from 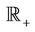 into
into 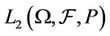 such that for each
such that for each ,
,  satisfies the integral equation P-a.e. showing that the Itô integral is an element of
satisfies the integral equation P-a.e. showing that the Itô integral is an element of 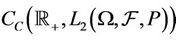 will make feasible the assumption that we wish to make that the integral is an element of D, a Banach space contained in the topological space mentioned For convenient we shall denote the Itô integral by
will make feasible the assumption that we wish to make that the integral is an element of D, a Banach space contained in the topological space mentioned For convenient we shall denote the Itô integral by

Theorem 2.1 For

Proof Fix 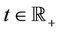 Then
Then
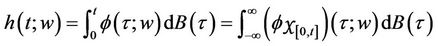
Thus
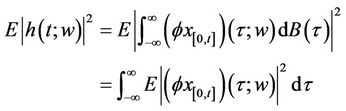
by lemma 1.3.
Hence .
.
Therefore for fixed t,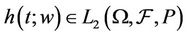 . Now let
. Now let  in
in . To show that
. To show that 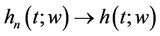 in
in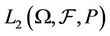 , it is sufficient to show that
, it is sufficient to show that

can be made arbitrarily small. That is, we must show that
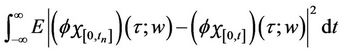
Can be made arbitrarily small. Choose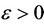 . Consider the nonnegative function
. Consider the nonnegative function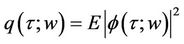 . By condition 3)
. By condition 3) 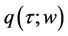 is integrable over
is integrable over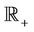 . Hence there exists a
. Hence there exists a 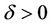 such that for every set of Lebesgue measure less than
such that for every set of Lebesgue measure less than ,
,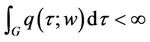 . Thus
. Thus
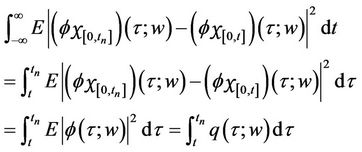
Since for 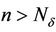 and
and  and since the Lebesgue measure of the interval
and since the Lebesgue measure of the interval 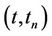 is its length, we conclude that the Lebesgue measure of
is its length, we conclude that the Lebesgue measure of 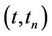 is less than
is less than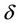 .
.
Hence
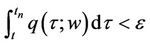
Implying that 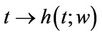 is continuous from
is continuous from  into
into 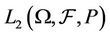 and the proof is complete.
and the proof is complete.
Since we have shown that 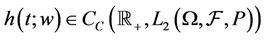 , we can conclude that the stochastic integral Equation (2.1) possesses a unique random solution
, we can conclude that the stochastic integral Equation (2.1) possesses a unique random solution
4. On Itô-Doob-Type Stochastic Integral Equations
In this section we shall study the existence and uniqueness of a random solution to a stochastic integral equation of the form
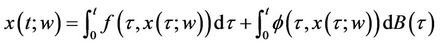 (3.1)
(3.1)
where . As before, the first integral is a Lebesgue integral, while the second is an Itô-type stochastic integral defined with respect to a scalar Brownian motion process
. As before, the first integral is a Lebesgue integral, while the second is an Itô-type stochastic integral defined with respect to a scalar Brownian motion process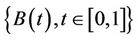 .
.
Recall that
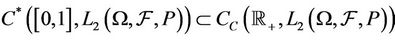 , We shall define the operators
, We shall define the operators  and
and  from
from  into
into 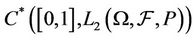 by
by
 (3.2)
(3.2)
and
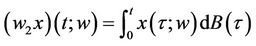 (3.3)
(3.3)
Note that in view of lemma 1.5 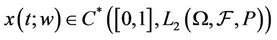 . Its clear that
. Its clear that 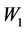 and
and 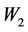 are linear operators.
are linear operators.
Theorem 3.1 The operators 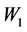 and
and 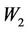 defined by (3.2) and (3.3) respectively, are continuous operators from
defined by (3.2) and (3.3) respectively, are continuous operators from 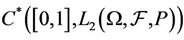 into
into .
.
Lemma 3.1 Let T be a continuous operator from  into itself. If B and D are Banach spaces stronger than
into itself. If B and D are Banach spaces stronger than 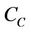 and the pair (B, D) is admissible with respect to T. Then T is a continuous operator from B to D.
and the pair (B, D) is admissible with respect to T. Then T is a continuous operator from B to D.
Proof of theorem 3.1 The fact that 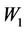 is a continuous operator from
is a continuous operator from  into
into 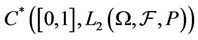 follows from lemma 3.1. From (3.3) we have
follows from lemma 3.1. From (3.3) we have
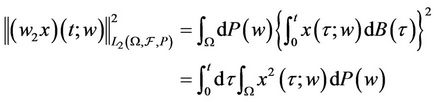
Furthermore
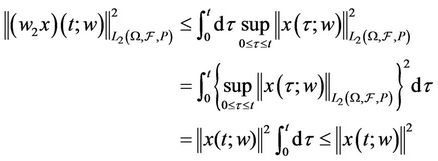
Therefore
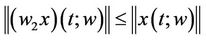
Thus 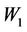 and
and 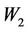 are continuous operators from
are continuous operators from 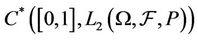 into
into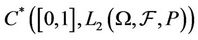 .
.
An Existence Theorem
We shall assume that lemma 3.1 holds with respect to the operators 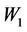 and
and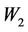 . Therefore there exist positive constants
. Therefore there exist positive constants  and
and 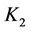 less than one such that
less than one such that
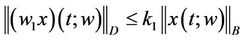 and
and 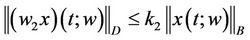
The following theorem gives sufficient conditions for the existence of a unique random solution, a second order stochastic process, to the Itô-Doob stochastic integral Equation (3.1).
Theorem 3.2 Consider the stochastic integral equation (3.1) under the following condition:
1) B and D are Banach spaces in
 which are stronger than
which are stronger than
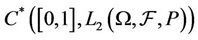 such that
such that 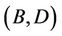 is admissible with respect to the operators
is admissible with respect to the operators 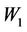 and
and 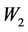
2) a) 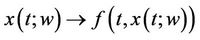 is an operator on
is an operator on
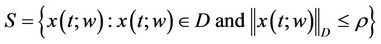
With values in B satisfying
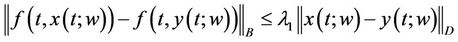
b)  is an operator on S into B satisfying
is an operator on S into B satisfying

where 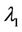 and
and 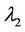 are constants. Then there exists a unique random solution to Equation (3.1) provided that
are constants. Then there exists a unique random solution to Equation (3.1) provided that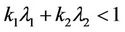 . And
. And
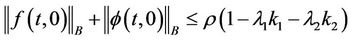
Proof. Define an operator U from the set S into D as follows
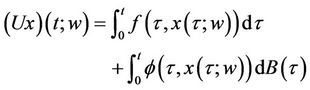
We need to show that U is a contraction operator on S and that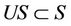 .
.
Let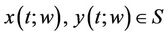 .
.
Then 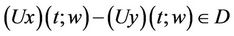 because D is a Banach space. Further, we have
because D is a Banach space. Further, we have
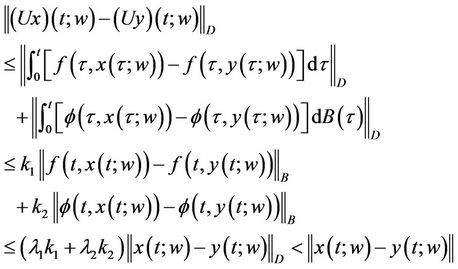
Thus U is a contraction operator.
For any element in S we have

Since  it follows that
it follows that
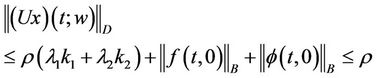
from the assumptions in the theorem.
Thus the existence and uniqueness of a random solution to Equation (3.1) follow from the Banach fixed-point theorem.
Theorem 3.4 (S. Banach’s fixed-point principle) ([11]).
If T is a contraction operator on a complete metric space H. then there exists a unique point 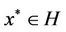 for which
for which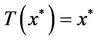 .
.
5. Conclusion
We investigated the existence and uniqueness of Itô stochastic integral equation by applying the theoretical techniques of probabilistic functional analysis. In fact author of [12] refers to probabilistic functional analysis as being concerned with the applications and extensions of the methods of functional analysis to the study of the various concepts, processes, and structures which arise in the theory of probability and its applications. Finally to develop and unify the theory of stochastic or random equations see [13-15].
REFERENCES
- K. Ito, “Stochastic Integral,” Proceedings of the Imperial Academy, Vol. 20, No. 8, 1944, pp. 519-524. doi:10.3792/pia/1195572786
- J. L. Doob, “Stochastic Processes,” Wiley, New York, 1953, pp. 426-432.
- Y. Dynkin, “Markov Processes,” Academic Press, New York, 1964, pp. 9-13.
- A. Jazwinski, “Stochastic Processes and Filtering Theory. Mathematics in Science and Engineering,” Vol. 64, Academic Press, New York, 1970, pp. 97-105
- K. Ito, “On a Stochastic Integral Equation,” Proceedings of the Japan Academy, Vol. 22, No. 2, 1946, pp. 32-35. doi:10.3792/pja/1195572371
- H. P. Mckean, “Stochastic Integrals,” Academic Press, New York, 1969, pp. 21-25.
- T. L. Satty, “Modern Nonlinear Equations,” McGrowHill, New York, 1967, pp. 216-226.
- L. Gikhmann and A. V. Skorokhod, “Introduction to the Theory of Random Process-Saunders,” Philadehphia, Pennsylvania, 1969, pp. 378-391.
- R. L. Stratonovich, “A New Representation for Stochastic Integrals and Equations,” Journal of SLAM Control, Vol. 4, 1966, pp. 362-371.
- E. Wong and M. Zakai, “On the Relation between Ordinary and Stochastic Differential Equations,” International Journal of Engineering Science, Vol. 3, No. 2, 1965, pp. 213-229. doi:10.1016/0020-7225(65)90045-5
- I. P. Natanson, “Theory of Functions of a Real Variable,” Vol. II, Ungar, New York, 2010.
- A. T. Bharucha-Reid, “On the Theory of Random Equations,” Proceedings of Symposia in Applied Mathematics, Vol. 16, 1964, pp. 40-69.
- G. Adomain, “Random Operator Equations in Mathematical Physics,” Journal of Mathematical Physics, Vol. 11, No. 3, 1970, pp. 1069-1074. doi:10.1063/1.1665198
- G. Adomain, “Linear Random Operator Equations in Mathematical Physics III,” Journal of Mathematical Physics, Vol. 12, No. 9, 1971, pp. 1944-1948. doi:10.1063/1.1665827
- G. Adomain, “Theory of Random Systems,” Transactions of the fourth Prague Conference on Information Theory, Statistical Decision Functions, Random Processes, Prague, 31 August-11 September 1965, pp. 205-222.

