Applied Mathematics
Vol. 3 No. 6 (2012) , Article ID: 20290 , 4 pages DOI:10.4236/am.2012.36094
Bounds for the Second Largest Eigenvalue of Real 3 × 3 Symmetric Matrices with Entries Symmetric about the Origin
1,3Department of Pure and Applied Mathematics, Jomo Kenyatta University of Agriculture and Technology, Nairobi, Kenya
2Department of Pure and Applied Mathematics, Kenya Polytechnic University College, Nairobi, Kenya
Email: geoffreyonkundi@yahoo.com
Received April 3, 2012; revised May 3, 2012; accepted May 10, 2012
Keywords: Bounds; Determinant; Eigenvalues; Trace
ABSTRACT
Let 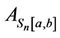 denote a set of all real nxn symmetric matrices with entries in the interval
denote a set of all real nxn symmetric matrices with entries in the interval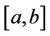 . In this article, we present bounds for the second largest eigenvalue
. In this article, we present bounds for the second largest eigenvalue  of a real symmetric matrix A, such that
of a real symmetric matrix A, such that .
.
1. Introduction
Throughout this article, 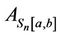 denotes a set of
denotes a set of 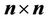 real symmetric matrices whose entries are in the interval
real symmetric matrices whose entries are in the interval . Eigenvalues of any real
. Eigenvalues of any real 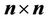 symmetric matrix A, will be represented by
symmetric matrix A, will be represented by
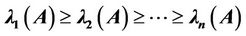 (1.1)
(1.1)
The smallest 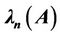 and the largest
and the largest 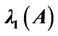 eigenvalues have been studied extensively in the recent decades. Recently, many researchers have turned attention to the second largest eigenvalue
eigenvalues have been studied extensively in the recent decades. Recently, many researchers have turned attention to the second largest eigenvalue 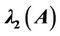 due to its applications in science and engineering. For example, thesecond largest eigenvalue governs the rate at which the statistics of the Markov chain converge to equilibrium. Here, we investigate bounds for
due to its applications in science and engineering. For example, thesecond largest eigenvalue governs the rate at which the statistics of the Markov chain converge to equilibrium. Here, we investigate bounds for 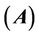 when entries of A vary in the interval
when entries of A vary in the interval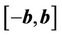 .
.
In 1985, Constantine [1] showed that if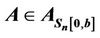 , then
, then
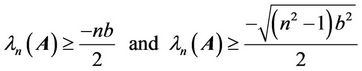 (1.2)
(1.2)
if n is even and odd respectively. Similar results are presented in [2]. In [3], Zhan gave bounds for both the largest eigenvalue 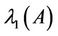 and the smallest eigenvalue
and the smallest eigenvalue 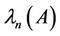 when entries of A are in a general interval
when entries of A are in a general interval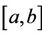 . In the same paper [3], Zhan posed the following problem: For a given integer j with
. In the same paper [3], Zhan posed the following problem: For a given integer j with , find
, find
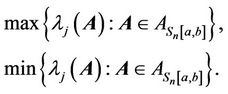 (1.3)
(1.3)
We are concerned with the case j = 2 when 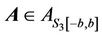 . We employ analytical approach discussed in [4] and the properties
. We employ analytical approach discussed in [4] and the properties
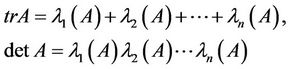 (1.4)
(1.4)
to determine these bounds. The following result will prove useful later. If 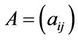 is any real 3 × 3 matrix such that
is any real 3 × 3 matrix such that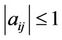 , then
, then 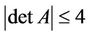 [5,6]. It immediately follows that if
[5,6]. It immediately follows that if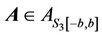 , then
, then
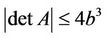 (1.5)
(1.5)
This paper is organized as follows. In Section 2, analytical method for eigenvalues of real 3 × 3 symmetric matrices is discussed. In Section 3, we derive bounds for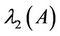 . Finally, a numerical example is given in Section 4.
. Finally, a numerical example is given in Section 4.
2. Analytical Calculation of Eigenvalues
A detailed description of this technique can be found in [4]. Let
 (2.1)
(2.1)
be a real 3 × 3 symmetric matrix. Eigenvalues of A can be directly calculated by solving the corresponding characteristic equation
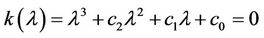 (2.2)
(2.2)
where,
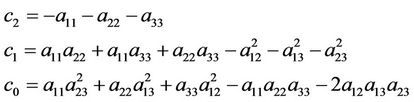 (2.3)
(2.3)
Equation (2.2) is then solved by first depressing it, i.e., transforming it to the form
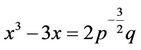 (2.4)
(2.4)
with,
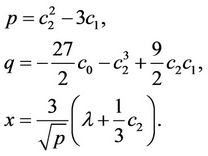 (2.5)
(2.5)
Solutions to Equation (2.4) are given by
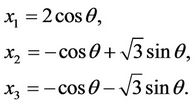 (2.6)
(2.6)
where,
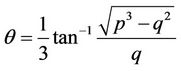 (2.7)
(2.7)
Finally, eigenvalues of A becomes
 , for
, for 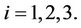 (2.8)
(2.8)
3. Bounds for the Second Largest Eigenvalue 
Note that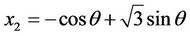 , corresponds to the second largest eigenvalue. We therefore determine the values of x2, p and c2 which minimizes or maximizes
, corresponds to the second largest eigenvalue. We therefore determine the values of x2, p and c2 which minimizes or maximizes . However, this is not straight forward since x2, p and c2 depends on the entries of A which vary in the interval
. However, this is not straight forward since x2, p and c2 depends on the entries of A which vary in the interval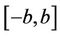 . We shall heavily rely on minimizing or maximizing
. We shall heavily rely on minimizing or maximizing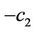 .
.
For the lower bound we require the largest possible value of p such that x2 and 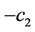 are minimum. Observe that if we put
are minimum. Observe that if we put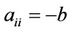 , then
, then
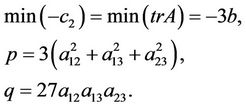 (3.1)
(3.1)
Setting 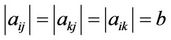 such that
such that
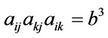 (3.2)
(3.2)
where  with
with 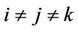 we obtain,
we obtain,
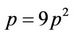 and
and .(3.3)
.(3.3)
Thus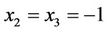 , as required. These correspond to the eigenvalues:
, as required. These correspond to the eigenvalues:
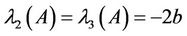 (3.4)
(3.4)
Now, suppose there exist 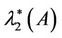 and
and  such that
such that
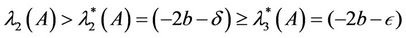 (3.5)
(3.5)
for some real numbers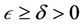 . Note that
. Note that
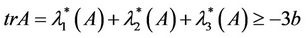 (3.6)
(3.6)
Therefore we must have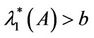 . However, this is impossible since from (1.5) we have
. However, this is impossible since from (1.5) we have
 (3.7)
(3.7)
We thus deduce that . Equality is attained by the following matrices:
. Equality is attained by the following matrices:
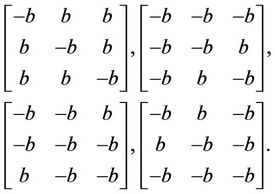 (3.8)
(3.8)
Similarly, for the upper bound, we require the largest possible value of p such that x2 and 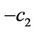 are maximum. Note that setting
are maximum. Note that setting 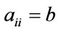 yields
yields
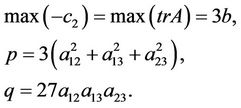 (3.9)
(3.9)
Now, if we put  such that
such that
 (3.10)
(3.10)
where 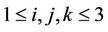 with
with 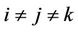 we have,
we have,
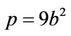 and
and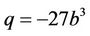 .
.
Check that
 60˚
60˚
and hence , corresponding to the eigenvalues:
, corresponding to the eigenvalues:
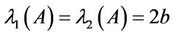 (3.13)
(3.13)
Again, assume there exist 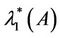 and
and 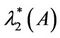 such that
such that
 (3.14)
(3.14)
for some real numbers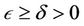 . Considering the fact
. Considering the fact
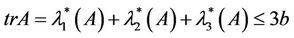 (3.15)
(3.15)
we necessarily have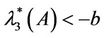 . Again from (1.5) we obtain
. Again from (1.5) we obtain
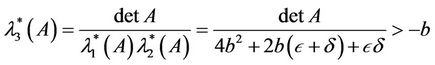 (3.16)
(3.16)
This is a contradiction and hence we conclude that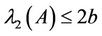 . Equality is attained by the following matrices:
. Equality is attained by the following matrices:
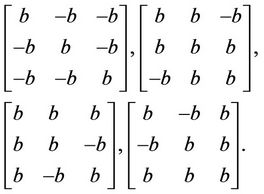 (3.17)
(3.17)
4. Numerical Example
Let . We first consider the lower bound for
. We first consider the lower bound for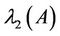 . According to Equation (2.8), we require
. According to Equation (2.8), we require , so that
, so that
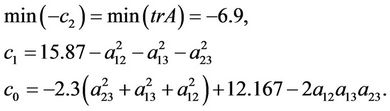 (4.1)
(4.1)
Substituting (4.1) into (2.5) yields
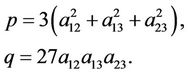 (4.2)
(4.2)
Now, p is maximum when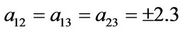 . However, by noting that
. However, by noting that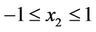 , we require
, we require . Thus we must have
. Thus we must have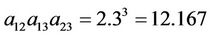 , with
, with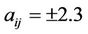 . Finally, from (2.6), (2.7) and (4.2), we easily have
. Finally, from (2.6), (2.7) and (4.2), we easily have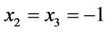 , corresponding to the eigenvalues
, corresponding to the eigenvalues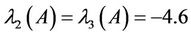 . We now let
. We now let  and
and 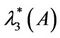 be eigenvalues such that
be eigenvalues such that ![]() for some real numbers
for some real numbers . It immediately implies that
. It immediately implies that
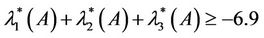 (4.3)
(4.3)
However, (4.3) is valid only if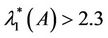 . Applying (1.4) results in
. Applying (1.4) results in

Note that

where  is the maximum determinant of a real 3 × 3 matrix whose entries are in a unit closed disc. Thus
is the maximum determinant of a real 3 × 3 matrix whose entries are in a unit closed disc. Thus . The minimizing matrices readily follow from (3.8). For the upper bound we set
. The minimizing matrices readily follow from (3.8). For the upper bound we set  2.3, giving
2.3, giving
 (4.4)
(4.4)
Substituting (4.4) into (2.5) results in
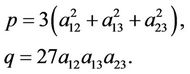 (4.5)
(4.5)
It is easy to check that if , such that
, such that , then
, then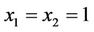 . This correspond to the eigenvalues
. This correspond to the eigenvalues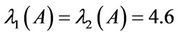 . Similarly if we let
. Similarly if we let 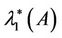 and
and 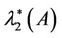 such that
such that
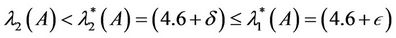 then
then
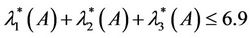 (4.6)
(4.6)
Check that (4.6) holds only if . However,
. However,
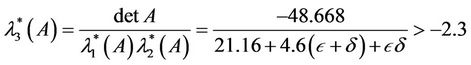
Thus  and the maximizing matrices follow from (3.17).
and the maximizing matrices follow from (3.17).
5. Acknowledgements
Thanks are due to the late Professor Cecilia Mwathi for her support during the initial stages of this research.
REFERENCES
- G. Constantine, “Lower Bounds for the Spectra of Symmetric Matrices with Nonnegative Entries,” Linear Algebra and its Applications, Vol. 65, 1985, pp. 171-178. doi:10.1016/0024-3795(85)90095-3
- R. Roth, “On the Eigenvectors Belonging to the Minimum Eigenvalue of an Essentially Nonnegative Symmetric Matrix with Bipartite Graph,” Linear Algebra and Its Applications, Vol. 118, 1989, pp. 1-10. doi:10.1016/0024-3795(89)90569-7.
- X. Zhan, “Extremal Eigenvalues of Real Symmetric Matrices with Entries in an Interval,” Siam Journal of Matrix Analysis and Applications, Vol. 27, No. 3, 2006, pp. 851-860. doi:10.1137/050627812
- J. Kopp, “Efficient Numerical Diagonalization of 3 × 3 Hermitian Matrices,” International Journal of Modern Physics C, Vol. 19, No. 3, 2008, pp. 523-548. doi:10.1142/S0129183108012303
- J. Brenner, “Hadamard Maximum Determinant Problem,” The American Mathematical Monthly, Vol. 79, No. 6, 1972, pp. 626-630.
- N. J. A. Sloan and P. Simon, “The Encyclopaedia of Integer Sequences,” Academic Press Inc., London, 1995.

