Advances in Chemical Engineering and Science
Vol.05 No.03(2015), Article ID:58420,10 pages
10.4236/aces.2015.53042
Solubility of Solids in Supercritical Fluids: The Mendez-Santiago Teja Model Revisited
Loubna Nasri1*, Zouhir Bensetiti2
1Departement of Pharmaceutical Engineering, University of Constantine 3, Constantine, Algeria
2Unisignal Inc., Brossard, Canada
Email: *loubnanasri@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 July 2015; accepted 25 July 2015; published 29 July 2015
ABSTRACT
For the development and enhancement of supercritical applications, it is crucial to know the solubility of the considered compound in the supercritical fluid (SCF) in order to determine the conditions to achieve the best outcome. Many models have been developed to calculate supercritical solubility behavior and most can be either a semi empirical relationship or based on an equation of state. The Mendez-Santiago and Teja (MST) model is one of the most semiempirical models used. In this work, a review of the (MST) model from an accuracy and ability viewpoint is accomplished to give concise discussion and so to the proposition of a modification.
Keywords:
Supercritical Fluids, Solubility, Dilute Solutions, MST Model

1. Introduction
Supercritical-Fluid Extraction (SCFE) is a separation method for which increased interest is shown for cases where traditional separation methods such as distillation have become too expensive, or cannot be applied. The advantages of SCFE are well documented and several commercial applications have been reported [1] . Supercritical fluids are environmentally benign solvents; their properties that are interesting from an extraction viewpoint include the diffusion coefficient, the density and the viscosity. The design and the development of SCFE processes depend on the ability to model and predict accurately the solid-supercritical fluid equilibria. Many of the existing simple predictive models are not sufficiently accurate to apply in the design and development of these processes [2] . Even the more sophisticated models are subject to serious errors when they are used for calculations near critical points, an area of great interest in terms of supercritical extraction. An additional complication is that many of the solute molecules of interest are large and polar, while the solvent molecules such as carbon dioxide tend to be small and of low polarity. This makes the thermodynamics less amenable to the usual modeling methods [3] .
2. Background
Different models have been used to predict the solubility of solids in SCFs, such as theoretical equations of state or semiempirical equations. Theoretical models like cubic equation of state or perturbed equations need large and complicated computational methods and the knowledge of the solid properties [4] . The problem starts with the availability of these properties, acentric factor and critical properties cannot be determined experimentally in most cases, so they should be evaluated using predictive methods, like group contributions (GC). Different approaches are proposed in the literature, but it is quite common to encounter molecules for which the methods are not applicable [5] . The same situation occurs with the sublimation pressure which plays a dominant role in the correlation of solubility data. In many cases, this quantity cannot be measured since its value is below the limit of any experimental method. Also for this property, GC methods have been suggested in the literature, but one has no way of controlling the validity of the calculated value [5] . Garnier et al. [6] stated that it was shown in the literature that the error in sublimation, which is very low for high molecular weight compounds, is in many cases responsible for large deviations between experimental and calculated solubilities. On the other hand, semiempirical equations like density based models do not need solid properties. They are based on simple error minimization and they use only available independent variables like pressure, temperature and density of pure solvent. The only drawback is the semiempirical character, which means that the solubility data are needed [4] . Recently, attempts have been reported to minimize the deficiency in prediction accuracy resulting from the error of sublimation pressures for non-volatile components that are used for the prediction of solubility solids in SFs [6] [7] . Among them we focus on the attempt of Mendez-Santiago and Teja [7] where they developed a simplified correlation to solid solubility data based on the theory of dilute solutions that was used earlier for the same purpose by Harvey [8] . In case of unavailability of sublimation pressure they have incorporated a Clausius- Clapeyron-type expression and derived a modified relation for the solid solubility.
In a previous work [9] , we have presented a methodology for the correlation and prediction of the solubility of some solids with different functional groups in different supercritical fluids. The methodology is based on the expanded liquid model theory which does not require the knowledge of the solute critical properties and sublimation pressure. For the comparison of results we have considered some literature models that account for effect of the system conditions in addition to the physical properties as sublimation pressure of the solute through their introduction of the enhancement factor such as those of Mendez-Santiago and Teja (MST). The results obtained show that for many of the 33 binary systems considered, the “modified” model of Mendez-Santiago and Teja gives better results (in term of average differences) than the original one. This was very surprising and motivates us to revisit the two models.
3. Solubility Correlation
Correlating the solubility to the fluid density is a common approach for modeling solid solubilities in SCF’s. Several authors have noticed that the logarithm of the solubility is a linear function of the density or sometimes of the logarithm of the density. The linearity of plots on these coordinates was first explained by Kumar and Johnston [10] in a derivation limited to the critical isotherms and they showed that this type of correlation is valid in the reduced density interval 0.5 ≤ rr ≤ 2.0 where rr º r/rc. A more general derivation was given by Harvey [10] who adapted the expression of Levelt Sengers [11] who has shown that near the critical point of the solvent, the expression for Henry’s constant can be simplified and may be written as:
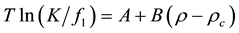 (1)
(1)
where T is the temperature, 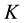 is Henry’s constant,
is Henry’s constant, 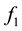 and
and 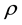 are the fugacity and density of the solvent at saturation,
are the fugacity and density of the solvent at saturation,  is the critical density of the solvent, and
is the critical density of the solvent, and 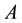 and
and 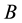 are constants. Harvey [8] worked with an effective Henry’s constant defined by
are constants. Harvey [8] worked with an effective Henry’s constant defined by
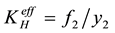 (2)
(2)
where  is the mole fraction solubility,
is the mole fraction solubility, 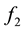 is the solute fugacity, which is fixed by the presence of an equilibrium solid phase and is proportional to the vapor pressure of the pure solid as follows:
is the solute fugacity, which is fixed by the presence of an equilibrium solid phase and is proportional to the vapor pressure of the pure solid as follows:
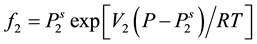 (3)
(3)
where  and
and 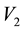 are the sublimation pressure and the molar volume of the solid. By substituting the fugacity in Equation (2) the effective Henry’s constant become:
are the sublimation pressure and the molar volume of the solid. By substituting the fugacity in Equation (2) the effective Henry’s constant become:
 (4)
(4)
Harvey [8] combined expression (1) and (4) to obtain:
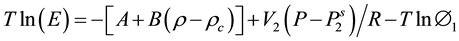 (5)
(5)
where E is the enhancement factor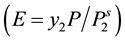 , and
, and 

Application of Equation (6) requires the sublimation pressure of the solute which is not available as stated in Section 2. Mendez-Santiago and Teja [7] circumvented this difficulty by the incorporation of a Clausius-Cla- peyron type expression and derived an equation with three adjustable parameters as below:

Correlation capability of Equations (6) and (7) are presented by Mendez-Santiago and Teja [7] in terms of absolute average difference AAD% between experimental and calculated solubilities:

At this point, reader can think obviously that if we have a common solute for which sublimation pressures are available and if these data are well represented by a Clausius-Clapeyron expression, Equation (6) and (7) must give the same AAD% (in the same range of T, P and for the same solubility data). But this is not the case, Mendez-Santiago and Teja [7] utilized Equations (6) and (7) for the same system solid-SC carbon dioxide just for two solutes: eicosanoic acid and myristic acid, and there is a difference of 33% between the AAD% of the two correlations. Also, previous results [9] show considerable differences between correlation utilizing Equations (6) and (7) for many systems among 33 systems solute-SCF considered. In fitting data, it’s known that increasing the number of model parameter will generally improve the correlation results, but in the case of Equation (7) the third parameter is not an additional one but it follows from the Clausius-Clapeyron expression.
From another point of view, to check the consistence and ability of Equations (6) and (7) we have reconsidered them for some systems presented in Table 1 as follows:

Using dimensionless equations is very useful as stated by Sparks et al. [12] , so by introducing reduced coordinates of solvent Equation (6) become:

where 

When sublimation pressure is not available, Equation (10) is decomposed as below:


A Clausius-Clapeyron-type expression for the sublimation pressure 
Table 1. Considered systems.
to apply Equation (12), (



From Table 2, if we note by 

And the parameter 

The difference between the two values of 
Table 2. Regression parameters and average deviations.
Figure 1. Histogram comparison of the different average differences.
Table 3. Solvents physical properties.
afrom reference [14] .
Table 4. Coefficients for sublimation pressure estimation and sublimation enthalpies of considered solids.
aData interpolated in this work, na/not available.
Table 5. References of solubility data.
The last point is based on the step of neglecting terms in Equation (5) which has not been argued by Mendez- Santiago and Teja [7] and some authors as Hansen et al. [39] stated that it was even a surprising step. So from the previous remarks, we can think that the neglected term (especially related to temperature) is for many systems solid-SCF non negligible.
For all these points, we opted for a modification to Equation (10) by adding a “correction” term proportional to the temperature without changing the original form as follows:

Subscript (m) is for the modification, and by introducing a cluasius-clapeyron expression for sublimation pressure, we can write:

Equation (16) can be presented as follows:

Thus, Equation (17) has the same form of Equation (14) but just with different parameters.
From Table 2 and Figure 1, we can see clearly that with the opted modification:
1) Correlation of data using Equation (15) and Equation (14) yield the same AAD%;
2) And if we note by 



4. Conclusion
This paper focuses on the application of the Mendez-Santiago Teja (MST) model for the correlation of solubility of solids in different supercritical fluids. Attention is paid to the presentation of the different limitations of the model. Analysis and results reported in this work show that a modification of the MST model is necessary. The modification proposed herewith keeps the simple form of original equations and is successful for all systems considered.
Cite this paper
LoubnaNasri,ZouhirBensetiti, (2015) Solubility of Solids in Supercritical Fluids: The Mendez-Santiago Teja Model Revisited. Advances in Chemical Engineering and Science,05,413-423. doi: 10.4236/aces.2015.53042
References
- 1. Coutsikos, P., Magoulas, K. and Kontogeorgis, G.M. (2003) Prediction of Solid-Gas Equilibria with the Peng-Robin- son Equation of State. The Journal of Supercritical Fluids, 25, 197-212.
http://dx.doi.org/10.1016/S0896-8446(02)00142-0 - 2. Cygnarowicz, M.L., Maxwell, R.J. and Seider, W.D. (1990) Equilibrium Solubilities of β-Carotene in Supercritical Carbon Dioxide. Fluid Phase Equilibria, 59, 57-71.
http://dx.doi.org/10.1016/0378-3812(90)85146-2 - 3. Ashour, I., Almehaideb, R., Fateen, S.-E. and Aly, G. (2000) Representation of Solid-Supercritical Fluid Phase Equilibria Using Cubic Equations of State. Fluid Phase Equilibria, 167, 41-61.
http://dx.doi.org/10.1016/S0378-3812(99)00314-3 - 4. Tabernero, A., del Valle, E.M.M. and Galán, Má. (2010) A Comparison between Semiempirical Equations to Predict the Solubility of Pharmaceutical Compounds in Supercritical Carbon Dioxide. The Journal of Supercritical Fluids, 52, 161-174.
http://dx.doi.org/10.1016/j.supflu.2010.01.009 - 5. Cortesi, A., Kikic, I., Alessi, P., Turtoi, G. and Garnier, S. (1999) Effect of Chemical Structure on the Solubility of Antioxidants in Supercritical Carbon Dioxide: Experimental Data and Correlation. The Journal of Supercritical Fluids, 4, 139-144.
http://dx.doi.org/10.1016/S0896-8446(98)00119-3 - 6. Garnier, S., Neau, E., Alessi, P., Cortesi, A. and Kikic, I. (1999) Modeling Solubility of Solids in Supercritical Fluids Using Fusion Properties. Fluid Phase Equilibria, 158-160, 491-500.
http://dx.doi.org/10.1016/S0378-3812(99)00151-X - 7. Méndez-Santiago, J. and Teja, A.S. (1999) The Solubility of Solids in Supercritical Fluids. Fluid Phase Equilibria, 158- 160, 501-510.
http://dx.doi.org/10.1016/S0378-3812(99)00154-5 - 8. Harvey, A.H. (1990) Supercritical Solubility of Solids from Near-Critical Dilute-Mixture Theory. The Journal of Phy- sical Chemistry, 94, 8403-8406.
http://dx.doi.org/10.1021/j100385a009 - 9. Nasri, L., Bensaad, S. and Bensetiti, Z. (2013) Correlation and Prediction of the Solubility of Solid Solutes in Chemically Diverse Supercritical Fluids Based on the Expanded Liquid Theory. Advances in Chemical Engineering and Sci- ence, 3, 255-273.
http://dx.doi.org/10.4236/aces.2013.34033 - 10. Kumar, S.K. and Johnston, K.P. (1988) Modeling the Solubility of Solids in Supercritical Fluids with Density as the Independent Variable. The Journal of Supercritical Fluids, 1, 15-22.
http://dx.doi.org/10.1016/0896-8446(88)90005-8 - 11. Johanna, M.H. and Sengers, L. (1991) Solubility near the Solvent’s Critical Point. The Journal of Supercritical Fluids, 4, 215-222.
http://dx.doi.org/10.1016/0896-8446(91)90013-V - 12. Sparks, D.L., Hernandez, R. and Estévez, L.A. (2008) Evaluation of Density-Based Models for the Solubility of Solids in Supercritical Carbon Dioxide and Formulation of a New Model. Chemical Engineering Science, 63, 4292-4301.
http://dx.doi.org/10.1016/j.ces.2008.05.031 - 13. Goldfarb, J.L. and Suuberg, E. M. (2008) Vapor Pressures and Enthalpies of Sublimation of Ten Polycyclic Aromatic Hydrocarbons Determined via the Knudsen Effusion Method. Journal of Chemical & Engineering Data, 53, 670-676.
http://dx.doi.org/10.1021/je7005133 - 14. Prausnitz, J.M., Lichtenthaler, R.N., de Azevedo, E.G. (1999) Molecular Thermodynamics of Fluid-Phase Equilibria. 3rd Edition, Prentice Hall Inc., Engelwood Cliffs.
- 15. Schmitt, W.J. and Reid, R.C. (1986) Solubility of Monofunctional Organic Solids in Chemically Diverse Supercritical Fluids. Journal of Chemical & Engineering Data, 31, 204-212.
http://dx.doi.org/10.1021/je00044a021 - 16. McEachern, D.M., Sandoval, O. and Iniguez, J.C. (1975) Vapor Pressures, Derived Enthalpies of Sublimation, Enthalpies of Fusion, and Resonance Energies of Acridine and Phenazine, The Journal of Chemical Thermodynamics, 7, 299- 306.
http://dx.doi.org/10.1016/0021-9614(75)90069-5 - 17. Delle, S.A. (1997) The Vapor Pressure of Environmentally Significant Organic Chemicals: A Review of Methods and Data at Ambient Temperature. Journal of Physical and Chemical Reference Data, 26, 157-193.
http://dx.doi.org/10.1063/1.556006 - 18. Hansen, P.C. and Eckert, C.A. (1986) An Improved Transpiration Method for the Measurement of Very Low Vapor Pressure. Journal of Chemical & Engineering Data, 31, 1-3.
http://dx.doi.org/10.1021/je00043a001 - 19. Oliveira, J.A.S.A., Monte, M.J.S., Notario, R. and Ribeiro da Silva, M.D.M.C. (2014) Experimental and Computational Study of the Thermodynamic Properties. The Journal of Chemical Thermodynamics, 76, 56-63.
http://dx.doi.org/10.1016/j.jct.2014.03.005 - 20. Huang, Z.S., Kawi, S. and Chiew, Y.C. (2004) Application of the Perturbed Lennard-Jones Chain Equation of State to Solute Solubility in Supercritical Carbon Dioxide. Fluid Phase Equilibria, 216, 111-122.
http://dx.doi.org/10.1016/j.fluid.2003.10.004 - 21. Bardi, G., Malaspina, L. and Piacenti, V. (1973) Vapor Pressure and Sublimation Enthalpy of Anthraquinone and of 1,5- and 1,8-Dihydroxyanthraquinone. Journal of Chemical & Engineering Data, 18, 126-130.
http://dx.doi.org/10.1021/je60057a024 - 22. Sasse, K., N’guimbi, J., Jose, J. and Merlin, J.C. (1989) Tension de vapeur d’hydrocarbures polyaromatiques dans le domaine 10-3-10 Torr. Thermochimica Acta, 146, 53-61.
http://dx.doi.org/10.1016/0040-6031(89)87075-3 - 23. Da Silva, M.A.V. and Ribeiro, Monte, M.J.S. (1990) The Construction, Testing and Use of a New Knudsen Effusion Apparatus. Thermochimica Acta, 171, 169-183.
http://dx.doi.org/10.1016/0040-6031(90)87017-7 - 24. Eckert, Z. (1983) Correlation and Prediction of Solid-Supercritical Fluid Phase Equilibria. Industrial and Engineering Chemistry Process Design and Development, 22, 582-588.
http://dx.doi.org/10.1021/i200023a005 - 25. Colomina, M., Jimenez, P., Roux, M.V. and Turrion, C. (1979) Thermochemical Properties of Naphthalene Derivatives. V. Formation Enthalpies of 2,3-Dimethylnaphthalene. Anales de Química, 75, 620-624.
- 26. Stephenson, R.M. and Malanowski, S. (1987) Handbook of the Thermodynamics of Organic Compounds. Elsevier, New York.
http://dx.doi.org/10.1007/978-94-009-3173-2 - 27. Lide, D.R. (2001) CRC Handbook of Chemistry and Physics. 84th Edition, CRC Press, Boca Raton.
- 28. Baccanari, D.P., Novinski, J.A., Pan, Y.-C., Yevitz, M.M. and Swain, H.A. (1968) Heats of Sublimation and Vaporization at 25° of Long Chain Fatty Acids and Methyl Esters. Transactions of the Faraday Society, 64, 1201-1205.
http://dx.doi.org/10.1039/tf9686401201 - 29. Welsh, W.J., Tong, W., Collantes, E.R., Chickos, J.S. and Gagarin, S.G. (1997) Enthalpies of Sublimation and Formation of Polycyclic Aromatic Hydrocarbons (PAHs) Derived from Comparative Molecular Field Analysis (CoMFA): Application of Moment of Inertia for Molecular Alignment. Thermochimica Acta, 290, 55-64.
http://dx.doi.org/10.1016/S0040-6031(96)03048-1 - 30. Arshadi, M.R. (1974) Determination of Heats of Sublimation of Organic Compounds by a Mass Spectrometric-Knu- dsen Effusion Method. Journal of the Chemical Society, Faraday Transactions, 70, 1569-1571.
http://dx.doi.org/10.1039/f19747001569 - 31. Colomina, M., Roux, M.V. and Turrion, C. (1974) Thermochemical Properties of Naphthalene Compounds. II. Enthalpies of Combustion and Formation of the 1- and 2-Naphthols. The Journal of Chemical Thermodynamics, 6, 571-576.
http://dx.doi.org/10.1016/0021-9614(74)90044-5 - 32. Huang, C.-C., Tang, M., Tao, W.-H. and Chen, Y.-P. (2001) Calculation of the Solid Solubilities in Supercritical Carbon Dioxide Using a Modified Mixing Model. Fluid Phase Equilibria, 179, 67-84.
http://dx.doi.org/10.1016/S0378-3812(00)00483-0 - 33. Balson, E.W. (1947) Studies in Vapor Pressure Measurement, Part III.—An Effusion Manometer Sensitive to 5 × 10-6 Millimeters of Mercury: Vapor Pressure of D.D.T. and Other Slightly Volatile Substances. Transactions of the Faraday Society, 43, 54-60.
http://dx.doi.org/10.1039/tf9474300054 - 34. Oja, V. and Suuberg, E. M. (1998) Vapor Pressures and Enthalpies of Sublimation of Polycyclic Aromatic Hydrocarbons and Their Derivatives. Journal of Chemical & Engineering Data, 43, 486-492.
http://dx.doi.org/10.1021/je970222l - 35. Malaspina, L., Bardi, G. and Gigli, R. (1974) Simultaneous Determination by knudsen-Effusion Microcalorimetric Technique of the Vapor Pressure and Enthalpy of Vaporization of Pyrene and 1,3,5-Triphenylbenzene. The Journal of Chemical Thermodynamics, 4, 1053-1064.
http://dx.doi.org/10.1016/0021-9614(74)90067-6 - 36. Tochigi, K., Iizumi, T., Sekikawa, H., Kurihara, K. and Kojima, K. (1998) High-Pressure Vapor-Liquid and Solid-Gas Equilibria Using a Peng-Robinson Group Contribution Method. Industrial & Engineering Chemistry Research, 37, 3731- 3740.
http://dx.doi.org/10.1021/ie970060m - 37. Chickos, J.S. and Acree Jr., W.E. (2002) Enthalpies of Sublimation of Organic and Organometallic Compounds.1910- 2001. Journal of Physical and Chemical Reference Data, 31, 537-698.
http://dx.doi.org/10.1063/1.1475333 - 38. Nass, K., Lenoir, D. and Kettrup, A. (1995) Calculation of the Thermodynamic Properties of Polycyclic Aromatic Hydrocarbons by an Incremental Procedure. Angewandte Chemie International Edition in English, 34, 1735-1736.
http://dx.doi.org/10.1002/anie.199517351 - 39. Hansen, B.N., Harvey, A.H., Coelho, J.A.P., Palavra, A.M.F. and Bruno, T.J. (2001) Solubility of Capsaicin and β- Carotene in Supercritical Carbon Dioxide and in Halocarbons. Journal of Chemical & Engineering Data, 46, 1054- 1058.
http://dx.doi.org/10.1021/je000255s
NOTES
*Corresponding author.





