Journal of Modern Physics
Vol.4 No.6(2013), Article ID:33459,4 pages DOI:10.4236/jmp.2013.46115
Studies on Transport Properties of Fe3+: Li2O-K2O-CdO-B2O3 Glass System: An Evidence of Mixed Alkali Effect
1Department of Physics, University College, Kakatiya University, Warangal, India
2Department of Physics, University College of Science, Osmania University, Hyderabad, India
Email: gpadmaja06@yahoo.com, pkistaiah@yahoo.com
Copyright © 2013 G. Padmaja, P. Kistaiah. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 25, 2013; revised April 27, 2013; accepted May 21, 2013
Keywords: Glassy Materials; Electrical Transport; Mixed Alkali Effect (MAE)
ABSTRACT
The glasses of the type (30 − x)Li2O − xK2O − 10CdO − 59B2O3 doped with 1 mol% of Fe2O3 were prepared by melt quench technique and their non-crystallinility has been established by XRD studies. The glasses were investigated for room temperature density and electrical conductivity in the temperature range 300 - 523 K and in the frequency range 102 to 105 Hz. The frequency and temperature dependence of conductivity as dielectric constant are presented.
1. Introduction
Oxide glasses containing Transition Metal Ions (TMIs) are technologically important because of their switching behaviour. These glasses are of semiconducting in nature. TMIs in these glasses exist in more than one valance state and electrical conduction here is of polaronic in nature, where the hopping of charge carriers is from low valance state ion to a high valance state ion. Electrical properties of oxide glasses containing TMI along with the alkali ions will be of mixed type, i.e. polaron and ionic [1-3]. Boron Oxide (B2O3) is unique in its ability to transform between two local environments when they mixed with alkali content. These B2O3 containing Alkali borate glasses are an important class of materials for various technological applications like, solid state electrolytes, insulation materials, textile fiber glass etc. In alkali borate glasses the number of ionic sites increases in the high temperatures because of the conversion of co-ordination changes leading to increase in NBO [4-7]. When the second alkali is introduced into glasses, they exhibit remarkably lower conductivity and the conductivity passes through a deep minimum. This phenomenon is called “Mixed Alkali Effect” (MAE). This property of alkali glasses is useful in electrochemical devices such as solid state batteries, fuel cells, chemical sensors and smart windows [8,9]. Mixed alkali glasses have a lower dielectric constant than the corresponding single alkali glasses, and larger dielectric loss than the corresponding single alkali glasses. An electrodynamic interaction between different types of neighbouring alkali ions in glass network can account for the increase in the energy of thermal activation of the ions as found from ionic conducting measurements. When an ion of a different type happens to exist within the neighbourhood of the ion of interest, their interaction energy, which increases the total energy required for activation of either ion, effectively reduces the mobilities of both ions involved [10]. In the present study, a.c. conductivity and dielectric properties of Fe3+ doped (30 − x)Li2O − xK2O − 10CdO − 59B2O3 where x = 0, 10, 15, 20 and 30, glasses are studied through electrical transport properties and the results are discussed in the following sections.
2. Experimental
Multi - component glasses with the composition, (30 − x)Li2O − xK2O − 10CdO − 59B2O3 − 1Fe2O3, where x = 0, 10, 15, 20 & 30 (LKCBF) were prepared through standard melt quenching technique. Thus prepared glasses were characterized through XRD, DSC, density and molar volume measurements. For dielectric measurements, a thin coating of silver paint was applied to the two sides of the samples to serve as electrodes. The dielectric measurements were taken on ZENTE CH 3305 LCR meter in the frequency range 102 - 105 HZ in the temperature range 30˚C - 250˚C.
3. Results and Discussion
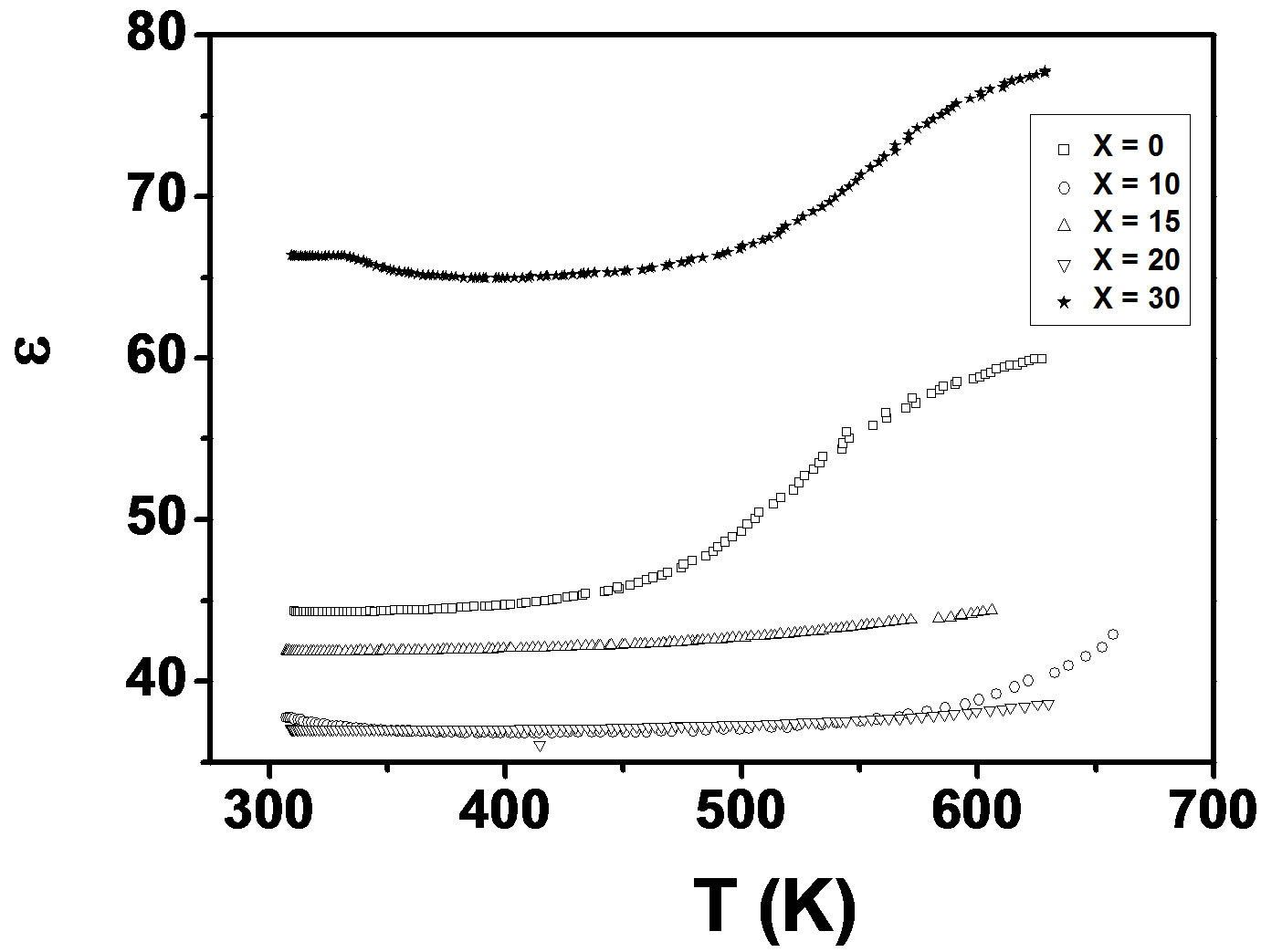
Figure 1(a) depicts the temperature dependence of dielectric constant (ε) and loss of LKCBF specimens at 100 KHz, respectively. The dielectric constant increases with temperature in x = 30 & 0 specimens and decreases in x = 10, 15, & 20 specimens. The variation of loss is also similar to the dielectric constant.
The a.c conductivity (σ) is calculated at different temperatures using the equation,
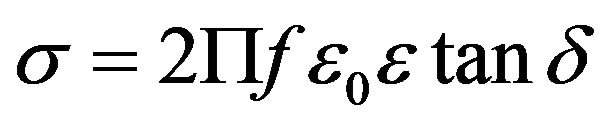 (1)
(1)
where f is frequency, ε0 is the vacuum dielectric constant, ε dielectric constant and tanδ is dielectric loss. Figure 1(b) shows a plot between σ vs 1000/T. The frequency dependence of dielectric constant ε and loss at 300 K in the range of 0 - 1 MHz for LKCBF specimens is shown in Figure 2. ε values at room temperature are found to decrease with the increasing frequency and dielectric loss also varies. Figure 3 shows the mixed alkali effect in dielectric constant values at different temperatures and different frequencies. Figure 4 shows mixed alkali effect at different temperatures and frequencies along with the concentration dependence of activation energy of LKCBF specimens.
From these plots, the activation energy for a.c conduction in the high temperature region over which a linear dependence of logσ with 1/T could be observed is calculated by fitting the data using least square fitting to the formulae [11],
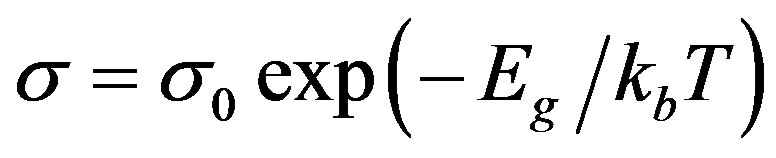 (2)
(2)
where σ0 is a prefactor, Eg is activation energy and k is Boltzmann’s constant.
The evaluated activation energy values are listed in Table 1 and compositional dependence is given in Figures 3 and 4. These values show a nonlinear trend in with the alkali ratio depicting the mixed alkali effect. The a.c. conductivity at 583 K for LKCBF specimens and 585 k for LKCBM specimens is listed in Table 1. These activation energies and conductivities vary non-linearly with the concentration of alkali ions.
In general the a.c conductivity of the amorphous materials, where charge carriers experience an approximately random potential energy, is found to obey the equation (Austin and Mott 1969) [12]
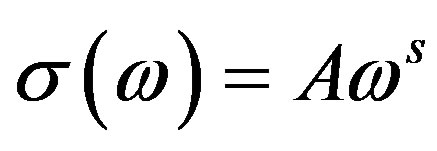 (3)
(3)
 (a)
(a) (b)
(b)
Figure 1. (a) Temperature dependence of e of LKCBF specimens at 100 KHz; (b) plot between s vs 1000/T of LKCBF specimens at 100 kHz.
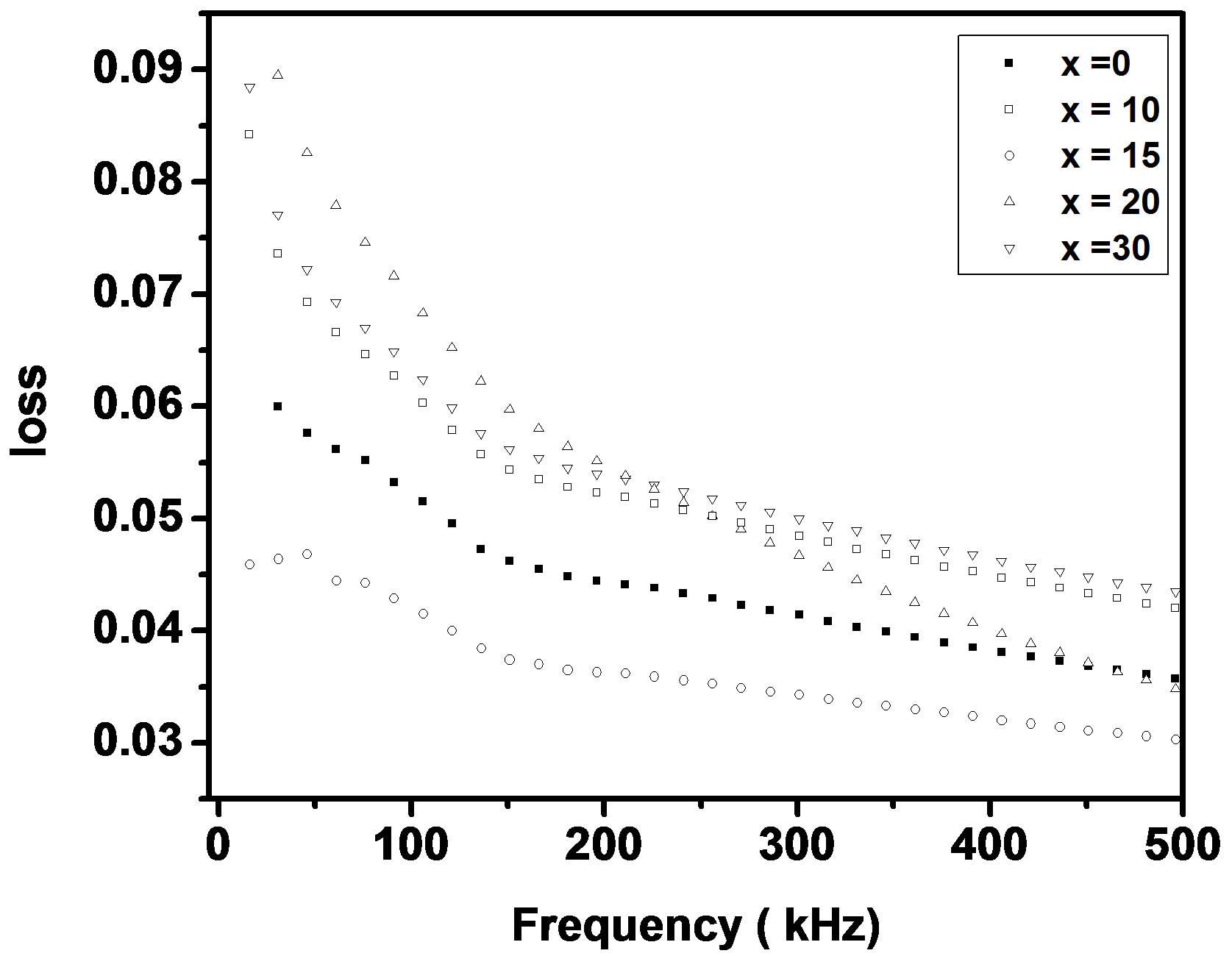
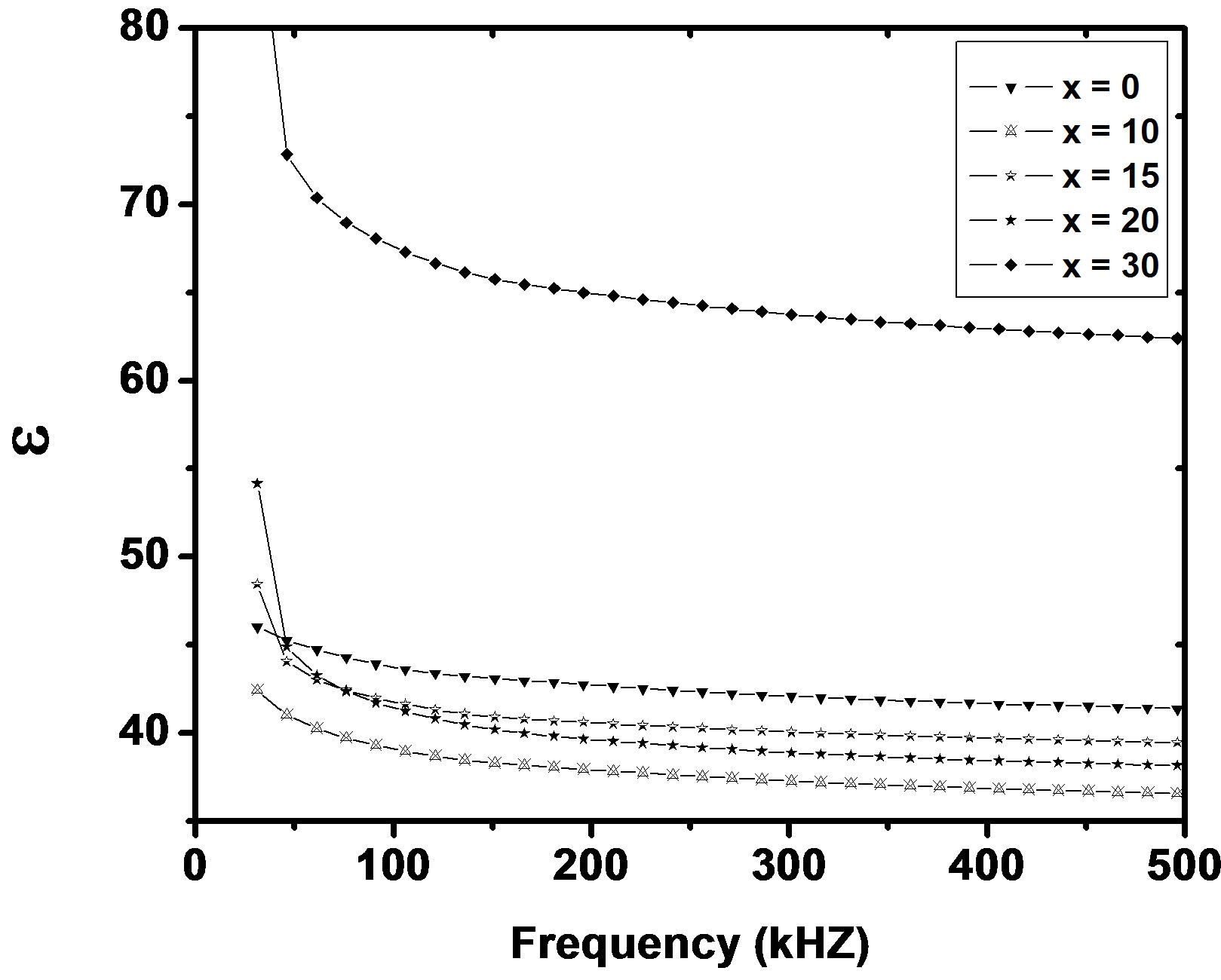
Figure 2. Frequency dependence of e and loss of LKCBF specimens.
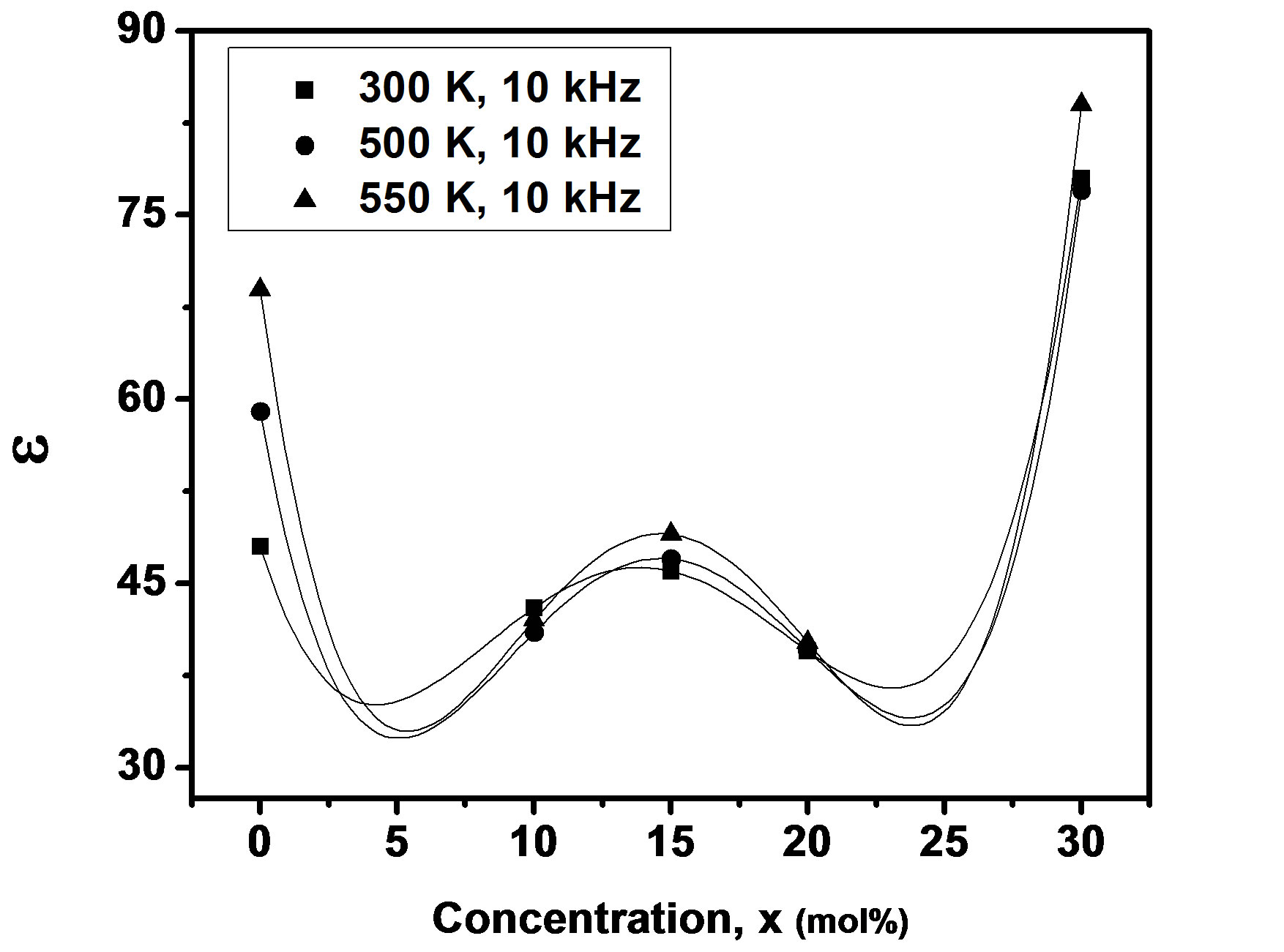
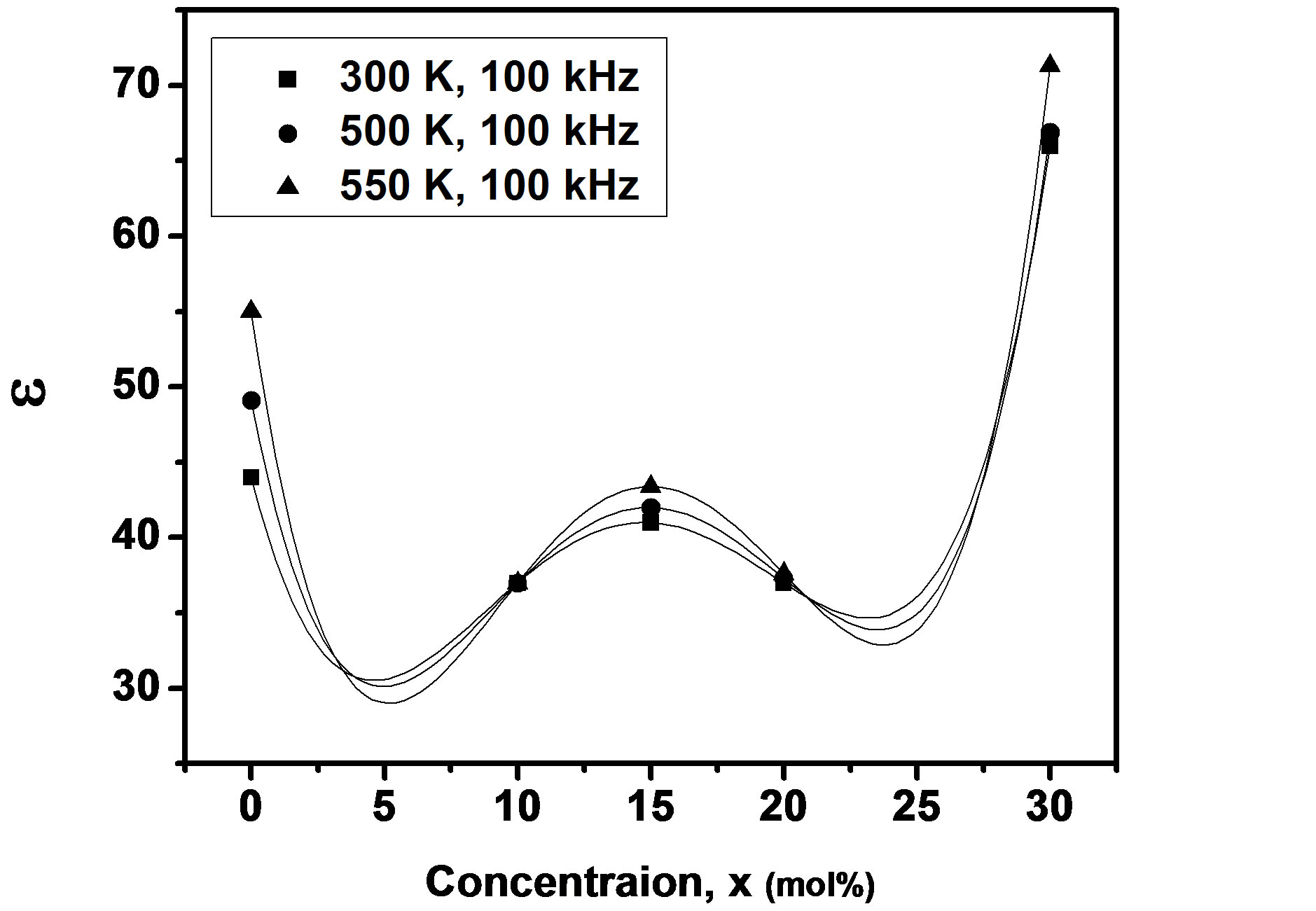
Figure 3. Concentration dependence of dielectric constant of LKCBF specimens.
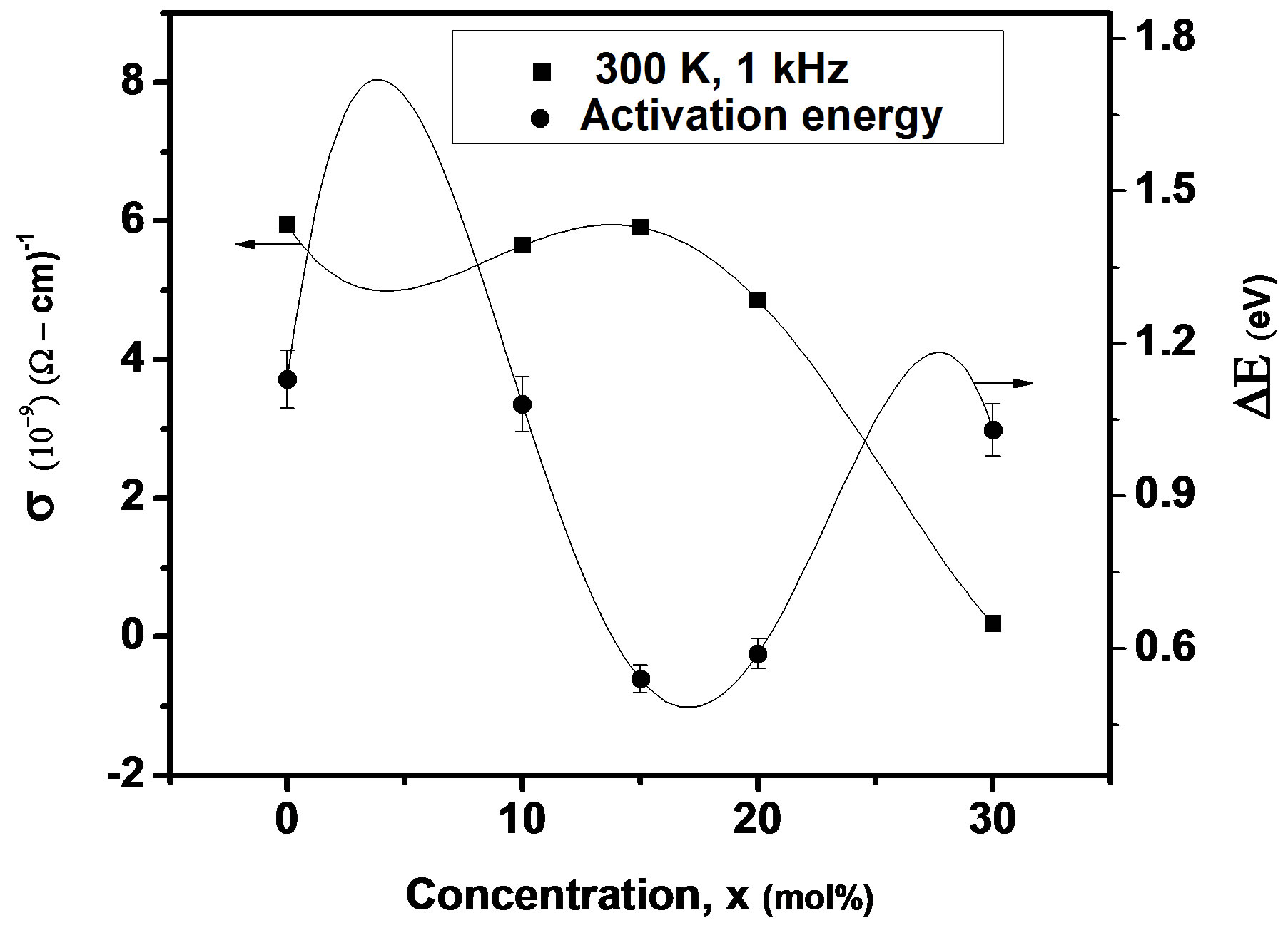
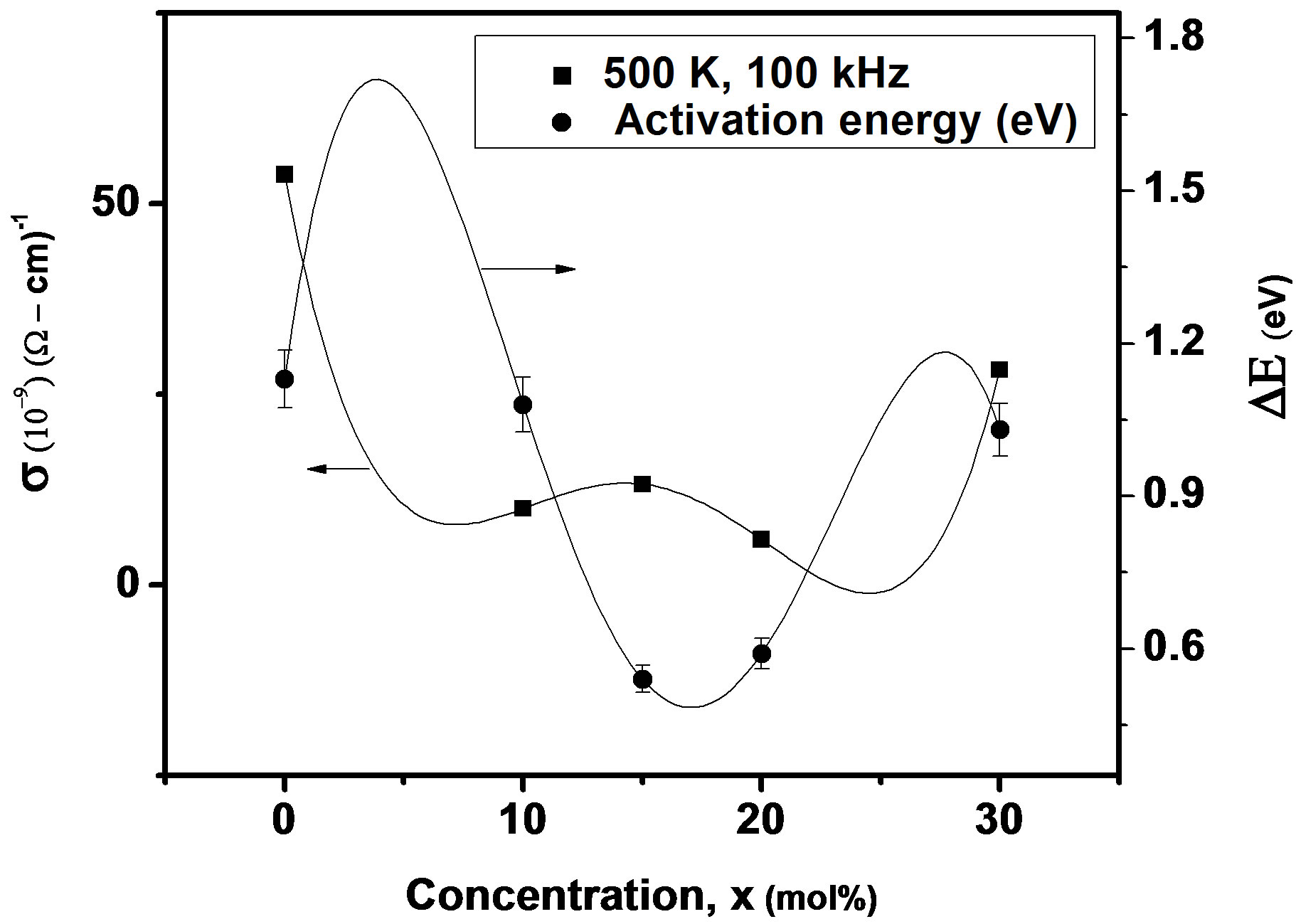
Figure 4. Concentration dependence of a.c conductivity and activation energy of LKCBF specimens at different temperatures and frequencies.
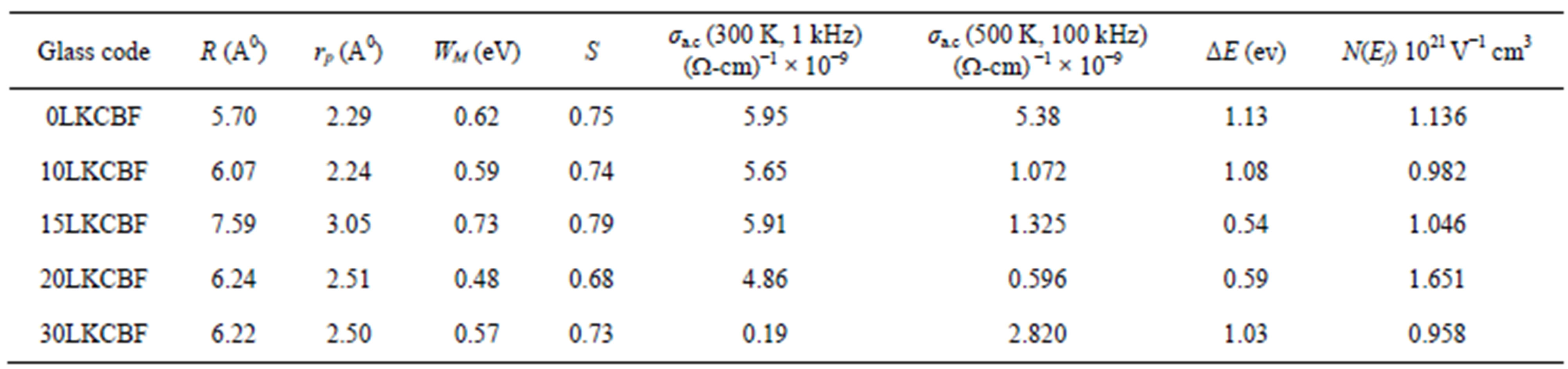
Table.1Evaluated polaron and transport parameters of KCBF glasses.
where A is constant, ω is frequency, s frequency exponent. Where s < 1 up to the frequency of 1 MHz .The frequency exponent S is defined as
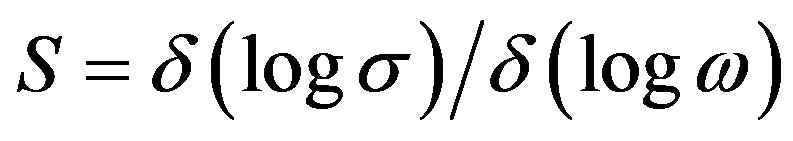 (4)
(4)
Here, the data has been analysed using HOB model. In this model the values of the exponent (s) are more than 0.8, which is permitted in the limit of the tunneling model, s is temperature dependent, the magnitude of s at any temperature is determined by the polaron binding energy (WM) in its localized states. The temperature dependent of s in this HOB model should follow an equation of the form [1]
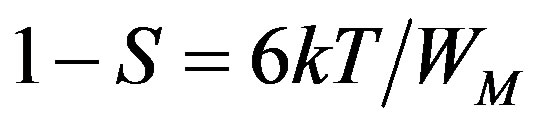 (5)
(5)
which indicate an almost constant value of s (~0.8) at different temperatures. In the present study we have calculated s at RT (300 k). The calculated S value lies between 0.68 - 0.79 for LKCBF specimens and WM value is observed to be in the range 0.48 - 0.73 eV for LKCBF specimens. Polaron radius (rp) and distance between polarons (R) and Density of states N(Ef) are also calculated and given in Table 1.
4. Conclusion
TMI doped K-Li borate glasses were prepared through melt-quenching method. The dielectric and conductivity properties were studied in detail. The observed activation energies and conductivities showed typical non-linear behaviour which was a manifestation of MAE. The emergence of MAE in these glasses was explained using Myuller and Stevel’s ideas.
5. Acknowledgements
One of the authors (G. Padmaja) thanks University Grants Commission, Govt. of India for providing financial assistance through merit fellowship.
REFERENCES
- M. M. El-Desoky Jr., Journal of Physics and Chemistry of Solids, Vol. 59, 1998, pp. 1659-1666. doi:10.1016/S0022-3697(97)00212-6
- G. B. Devidas, T. Sankarappa, B. K. Chougule and G. Prasad, Journal of Non-Crystalline Solids, Vol. 353, 2007, pp. 426-434.
- M. I. Mohammed, Kh. Abd-Allah and M. Y. Hassaan, Egyptian Journal of Solids, Vol. 27, 2004, p. 299.
- S. Murugavel and B. Roling, Physical Review B, Vol. 76, 2007, Article ID: 180202(R).
- K. S. Kim and P. J. Bray, Physics and Chemistry of Glasses, Vol. 15, 1974, p. 47.
- M. Gonguly, M. Harish Bhat and K. Rao, Materials Research Bulletin, Vol. 34, 1999, p. 1757.
- R. V. Aravekar, N. Devaji, G. Parthasaradhy, E. S. Rajagopal and Jr. Ramakrishna, Physics and Chemistry of Glasses, Vol. 30, 1989, p. 172.
- Y. Gao and C. Cramer, Solid State Ionics, Vol. 176, 2005, pp. 921-927. doi:10.1016/j.ssi.2004.11.010
- K. Hughes and J. O. Isard, In: J. H. Hladik, Ed., Physics of Electrolytes I, Academic Press, New York, 1972, p. 351.
- J. R. Hendrickson and P. J. Bray, Physics and Chemistry of Glasses, Vol. 13, 1972, p. 43.
- N. F. Mott and E. A. Davis, “Electronic Processes in NonCrystalline Materials,” Clarendon, Oxford, 1979.
- I. G. Austin and N. F. Mott, Advances in Physics, Vol. 18, 1969, p. 41. doi:10.1080/00018736900101267

