Received 8 December 2015; accepted 23 February 2016; published 26 February 2016

ABSTRACT

This paper has two parts, in this occasion we will present the first one. Until today, there are two formulations of classical mechanics. The first one is based on Newton’s laws and the second one is based on the principle of least action. In this paper, we will find a third formulation that is totally different and has some advantages in comparison with the other two formulations.

Keywords:

Classical Mechanics, Constant of Motion, Dissipation

1. Introduction

Until today, there are two formulations of classical mechanics. The first one is based on Newton’s laws and the second one is based on the principle of least action [1] . These formalisms have advantages and disadvan- tages. The main advantage of the second one compared to the first one is that it eliminates the constraint forces. The main disadvantage is that it has problems if the force does not come from a potential.

The objective of this paper is to introduce a new formulation that has some advantages (and disadvantages) compared to the above formalisms.

Suppose that there are n bodies interacting in a medium where the i-body is subjected to a force 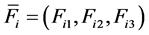that depends on the position of all bodies and to a drag force proportional to the square of the velocity given by

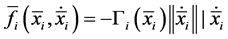(1)

where is the position of the center of mass of the i-body, is the euclidean norm and is given by 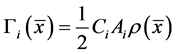[2]

(2)

where is the transverse motion area of the i-body, 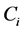is the drag coefficient which depends on the shape of the transverse motion surface and 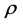is the medium density that depends on the position.

If we assume that the transverse motion surface of all bodies is constant along the time (this happens if the bodies are spheres or if they move only in one direction without rotation), then the equation of motion of the system, according to classical Newton’s second law, is given by

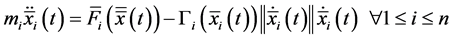(3)

where 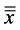is the matrix whose coefficients are.

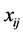On the one hand, in the vacuum case (), if 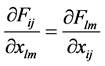it is well known that the following quantity is constant

(4)

where.

On the other hand, if there are just one body () moving in one direction and, it is also known that in the time interval, the following quantity is constant [3]

(5)

where, (which is constant because) and

(6)

(7)

In order to introduce our formalism, first we will find an equation equivalent to Equation (3) (we will call it the master equation of Equation (3)). We will say that our formalism is based on that equation. Then, from the master equation, we will try to generalize the constants of motion given in Equations (4) and (5) for the general case, i.e., for any medium and for the three dimensional case. Finally, we will see another advantage of the master equation. We will define the trajectory and the temporal equations and we will develop a more convenient algorithm for solving the equation of motion.

Notation: along this paper, we shall consider the variables t and. The derivatives respect to the variable t will be denoted by the symbol “” while the derivatives respect the variable will be denoted by the symbol apostrophe “”. In addition, if, we will denote:

•

•

•

•

•

2. Master Equation of Equation (3)

We propose as a solution of Equation (3) where

(8)

and will consider a time interval such that

(9)

Then we have

(10)

Let. There are two cases, or.

In the first case, using Equation (10) we obtain

Hence, the component j of Equation (3) becomes

(11)

In the second case, scaling by to both members of component j of Equation (3) it turns out to be equivalent to

(12)

We will call

(13)

(14)

and we will develop the two members of Equation (12).

///

Left member: using Equation (10) we have

Hence, according to Equations (13) and (14) we arrive to

(15)

Right member: using Equation (10) we have

(16)

In addition, since, then and hence. This implies that u does not change its sign and hence, if we arrive to

(17)

By Equations (13), (14), (16) and (17) and using that we obtain

(18)

Let

(19)

(20)

Using Equations (2), (19) and (20), Equation (18) turns

(21)

Finally, using Equation (21), the fact that and calling

(22)

we arrive to

(23)

///

Using Equations (15) and (23) we infer that Equation (12) becomes

(24)

On the other hand, using Equations (10), (13) and (14) we have

where

(25)

Then, if we use the fact that it follows that

(26)

Finally by Equations (24) and (26) we obtain the following set

(27)

This equation can be viewed as a differential equation of first order where is the unknown function. The solution is

(28)

Using Equations (11), (14) and (28) we finally obtain that Equation (3) is equivalent to

(29)

where, , , and are given in Equations (13), (19), (20), (22) and (25) respectively.

We will say that this is the master equation of Equation (3). It is worthwhile to point out that this equation is as important as Newton’s second law and that our formalism is based on this equation.

Note 1: using that the component j of Equation (3) implies Equation (12) we have that Equation (3) (and the master equation) implies

(30)

By taking and (which implies) in this equation, we also have that Equation (3) implies

(31)

where

(32)

(33)

Note 2: suppose that there is just one body and it moves only in one direction.

On the one hand, by condition (9), and hence is constant.

On the other hand, by Equation (20),

In addition, since and, then we have

Making a change of variable we finally obtain

(34)

where is given by Equation (6).

Note 3: in the vacuum case, i.e., when it is not necessary to ask condition (9).

3. Constant of Motion

In this section we will try to generalize the constants of motion given in Equations (4) and (5).

3.1. A Generic Constant of Motion

In Note 1 of the previous section, we saw that Equation (3) implies Equation (31). It follows that

Using the notation given at the beginning and that according to Equation (33) we arrive to

where

(35)

Since, it follows that

Hence, we obtain that the following quantity is a constant of motion

(36)

If we want to generalize the constants of motion of Equations (4) and (5) we need to express in function of and.

On the one hand, suppose that we have the following approximation

(37)

Hence, using Equations (25), (37) and the notation of the beginning we arrive to

(38)

On the other hand, using Equation (32) and the notation of the begining it is easily proved that

and then according to Equation (35) we have

If we call

(39)

we arrive to

If we want to write in function of, then there should be that satisfies

(40)

In that case we have

(41)

Hence, taking into account that is constant, it follows from Equations (36), (38) and (41) that the following quantity is a constant of motion

(42)

However, in order to satisfy Equation (40) we need that

(43)

Next we will prove that this equation is equivalent to

(44)

In addition, we will prove that if comes from a potential this equation becomes

(45)

///

Proof: we denote by.

According to Equation (39) we have

Since according to Equation (37) only depends on we arrive to

where is Kronecker’s delta.

Analogously we have

Hence, Equation (43) is equivalent to

Using the definition of Kronecker's delta it is easily proved that this equation is equivalent to Equation (44). In addition, if comes from a potential we have

and hence Equation (44) turns out to be equivalent to Equation (45).

///

Finally, if Equations (37) and (44) (or (45)) are satisfied, then the quantity given in Equation (42) is a constant of motion and it depends on and.

However, if comes from a potential, we can see that Equation (45) (the second one) has a problem since and are independent variables. Hence, this equation can be only satisfied in two particular cases, when (which implies) and when there is just one body (which implies and then).

Next, we will consider these two cases and we will obtain Equations (4) and (5) from Equation (42). In addition, we will obtain another constant of motion in the three dimensional case (with) under certain approximations.

3.2. Equations (4) and (5) and Another Constant of Motion

In the case, Equation (37) and (45) are necessarily satisfied and we can see in Equations (39) and (40) that is the potential of. Hence, taking into account that in this case, according to Equation (37), , we can obtain Equation (4) from Equation (42).

In the case where there is just one body Equation (45) becomes

(46)

where we omit the sub-index i, since.

In the one dimensional case, and then this equation is necessarily satisfied. In addition, we can use Equation (34) in order to satisfy Equation (37). Hence Equation (42) becomes:

where is given by Equation (6) and according to Equations (39) and (40) is given by Equation (7).

Scaling by to both members we obtain Equation (5).

In the three dimensional case, we will propose as a solution of Equation (46) the following

where V is the potential of.

We have

Then we can see that Equation (46) is satisfied.

In order to satisfy Equation (37), we shall approximate the function at the point by its Taylor polynomial of degree one.

Hence

(47)

According to Equation (32) and to the notation of the beginning we have

Then, if we differentiate Equation (37) we arrive to

Assuming that and taking into account that according to Equation (33) we obtain

(48)

Hence, Equation (47) becomes

(49)

According to Equation (48) its error is given by

where

Then, Equation (49) holds only if

(50)

We can see in this equation that there is a problem when. Then, in order to satisfy Equation (49) we necessarily have to ask. This problem cannot be solved even when we approach σ at a higher order, i.e., we cannot find a constant of motion depending on the position and velocity in a time interval where in this way.

We use Equations (39) and (40) and the fact that in order to find. We have

Hence, according to Equation (49) we arrive to

(51)

where and β is given by

(52)

Using Equations (49), (51) and (52) we finally obtain that Equation (42) becomes

Taking into account that and are constants and scaling this equation by we obtain that the following quantity is a constant of motion

(53)

where we are considering a time interval where Equation (50) holds.

4. Other Advantages of the Formalism

In this section, we will see other advantages of the formalism. First, we will see an interesting application of the master equation. By means of this equation, we will introduce two equations which are called the trajectory and the temporal equation respectively. Finally, we will develop a more convenient algorithm for solving the equation of motion.

Until now, we have considered in the master equation. We will see the consequences derived from taking. We will consider the vacuum case, taking into account that the general case is analogous. In this case by Equation (20) we have. Then, according to Equation (29), the master equation becomes

(54)

Equations (30) and (31) turns out to be

(55)

(56)

In addition, according to Equation (3), the equation of motion of the system is given by

(57)

Remember also that in this case it is not necessary to ask condition (9).

Next, we will see an application of the master equation.

4.1. An Application of the Master Equation

Let be the solution of Equation (57). This function is the parametrization of a certain curve given by

where is the curve described by.

Since represents the trajectory of the i-body, this curve represents the trajectory of the system. We are interested in the following problems:

1. Let be another parametrization of C.

The problem is to find which condition is satisfied by.

2. Suppose we have an arbitrary parametrization of the curve C.

The problem is to find a way to find the original parametrization from.

We solve these problems by using the master equation:

1. Let be a parametrization of C. Then, the original parametrization can be expressed like. In addition, we can suppose that there exists a function that satisfies Equation (8). Then, Equation (54) holds.

On the one hand, we know that this equation implies (55) and hence

Then we have

where means the relationship of parallelism (see Appendix).

Using Equation (10) and the identity we also have

Then we obtain that must satisfy the following condition

(58)

On the other hand, using Equation (54) we also have that implies Equation (11). Hence, must also satisfy the following conditions

(59)

(60)

Finally, if is a parametrization of C, it must satisfy conditions (58), (59) and (60).

2. Suppose we find a parametrization of C. Then, by the previous item, conditions (58), (59) and (60) must be satisfied.

By condition (58) we have

where i, j, l and m are indexes satisfying,.

In addition, there exists λ such that

(61)

By condition 60 we have

where i, j, l and m are indexes satisfying,.

Hence, we can define a function by the following prescription

(62)

where h can be any function, λ is given by Equation (61) and i, j, l and m are indexes satisfying and.

We will prove that this function u satisfies Equation (54) and

(63)

///

Proof: we will assume that is of class which implies that according to Equations (13) and (22)

and are continuous functions and they are well defined in J.

Let, and. We shall proceed according to the following three cases, , and, or. We will prove that in all cases we obtain Equation (54).

Case: in this case, by condition (59), we have and hence we obtain Equation (54) for.

Case and: there are two sub-cases, or.

In the first case, by Equation (62) for and, we obtain Equation (54) for.

In the second case, there exist l and m such that. Then, by Equation (62) for we have

Since and are continuous functions and are well defined in J, then u is also continuous and it is well defined in. Hence we have

In addition, since, there exists such that

Then we arrive to

Since this limit should exist and, then the following condition holds

Then, by l'Hopital's rule we have

Since we arrive to

Hence we have

Then we also obtain Equation (54) for.

Case: in this case we have that and hence, by Equation (62), we obtain Equation (54) for.

In all cases we obtain Equation (54). Then, we proved that the function u given in Equation (62) satisfies the master equation.

In order to prove Equation (63), let,. There are two cases, or.

In the first case, by Equation (61), and hence we obtain

In the second case, and hence by Equations (61) and (62) we obtain

Hence, by Equation (61) we also obtain

Since i and j were arbitrary, we finally proved that u satisfies Equation (63).

///

Let be such that with given in Equation (8).

On the one hand, we saw that u satisfies the master equation and hence satisfies Equation (3).

On the other hand, by condition (58), Equation (10) and the fact that we have

Then, is the solution of Equation (57) and it is the original parametrization of C.

According to the two solutions of the problems considered above, we can also conclude that the master equation is equivalent to conditions (58), (59) and (60) and to Equation (62).

Next, we will discuss the results obtained, we will give a name to Equations (8) and (58) and we will write them in a better way.

Note: suppose that. Then, satisfies condition (58). However, it satisfies conditions (59) and (60) if and only if. This result was expected since is a solution of Equation (57) if and only if it is an equilibrium point. Then, we can say that conditions (59) and (60) incorporates the constant solutions to the formalism.

4.2. Trajectory and Temporal Equations

According to the previous section, we have that is a parametrization of C if and only if it satisfies conditions (58), (59) and (60). Since C describes the trajectory of the system, then Equation (58) will be called the trajectory equation, taking into account that conditions (59) and (60) are just extra conditions for particular cases. However, there are two things to check in order to be sure that we are in the correct way.

The first one is that must be a solution of the trajectory equation, since it is a parametrization of C. This can be easily proved by using that satisfies Equations (56) and (57).

The second one is that if is a solution of the trajectory equation, then, given by, must be also a solution where. In order to prove this we require that and. In addition, we will prove that if satisfies conditions (59) and (60), then also satisfies them and that

(64)

///

Proof: on the one hand

On the other hand

where we made the change of variable and we used that and (which implies that is an increasing function).

Since

then there exists such that

This implies that

Hence, we arrive to

Using the results obtained before, this equation becomes

By calling

we finally have

Then, we proved that

In addition, since we have

Hence we arrive to

We finally proved that is a solution of the trajectory equation.

In order to prove conditions (59) and (60) we have

From these equations we can see that

Hence, using that satisfies conditions (59) and (60) we arrive to

Then, also satisfies conditions (59) and (60).

Finally, Equation (64) is easily proved by using that if and only if, if and only if and that

///

Next, we will write the trajectory equation in a better way. We will prove that it is equivalent to the following two equations

(65)

(66)

where we used the notation given at the beginning and in Equation (65), the sign ± has to be the same for all i.

///

Proof: on the one hand, since, then (see appendix) we have that

is equivalent to

In addition, is equivalent to. Hence, we only have to prove that Equation (58) implies and that Equations (65) and (66) imply. It is trivial to prove the first implication. Then, we will prove the second one.

Suppose that Equations (65) and (66) hold. From these equations we have

Evaluating this equation in we arrive to

Then, there exists λ such that

This implies that

On the other hand, since, then there exists such that:

where the sign of is the same for all i.

Hence we arrive to

There are two cases to consider, or.

In the first case, using this equation we have and then

In the second case we arrive to

Since the sign of is the same for all i, this implies that and hence we also have that

In both cases we obtain that

which implies.

///

On the one hand, note that in the one dimensional case, Equation (65) is already solved (except the condition). On the other hand, note that if there is just one body, i.e., when, Equation (66) is already solved. Due to this fact, we will call internal trajectory equation of the i-body to Equation (65) and external trajectory equation to Equation (66).

We will also baptize to Equation (8). Taking into account that it determines the relationship between the “real time” t and, we will call it the temporal equation. Sometimes, we will also call temporal equation to Equation (62).

We will prove that if the force comes from a potential V, then we can write this Equation (for) using the mechanical energy of the system as follows

(67)

where e is the energy.

///

Proof: on the one hand, we saw in the second answer of the previous section that the function u given in Equation (62) satisfies the master equation. On the other hand, we saw in Section 2 that the master equation implies Equation (55). Using the notation given at the beginning it follows that

In addition, if the force comes from a potential V we have

Then we obtain

where we used that is constant.

From this equation, we can easily obtain Equation (67).

///

Next, we will construct a more convenient algorithm for solving the equation of motion.

4.3. A More Convenient Algorithm for Solving the Equation of Motion

Using the results obtained before, we can construct the following algorithm in order to solve Equation (57):

1. Find a solution of the trajectory equation and check that it satisfies conditions (59) and (60).

2. Choose conveniently a function with and in order to build another solution given by.

3. Find the function u given in Equation (62) (or (67)).

4. Solve the temporal equation.

Finally, is the solution of Equation (57).

Note that the difficult step of this algorithm is the first one.

However, to find a solution of the trajectory equation is easier than to find the solution of Equation (57) for the following two reasons:

1. There are infinite solutions of the trajectory equation while there are just one solution of Equation (57). In addition, the solution of Equation (57) is also a solution of the trajectory equation.

2. According to the appendix, the trajectory equation is a system of equations while Equation (57) is a system of 3n equations.

Due to these facts, if we want to find the motion of the system, it is more convenient to follow this algori- thm.

In the second part of this paper, we will find a more convenient way of solving the temporal equation and then we will change the fourth step of this algorithm. We will also solve some examples using this formalism.

Note 1: in the second step, the phrase “choose conveniently a function” refers to choose so that the temporal equation can be solved easily.

Note 2: according to the appendix, the number of equations of the internal trajectory equation of the i-body is 2. In addition, the number of equations of the external trajectory equation is. Hence, the total number of equations remains.

Note 3: the set

is a system of equations. Hence, if we want to solve the trajectory equation, we have to find a function with that satisfies

and then solve the system of equations

5 Conclusions

We obtained an equation equivalent to Equation (3) (Equation (29)) and we called it the master equation. From this equation, we could deduce all the formalism.

We saw that if Equations (37) and (44) were satisfied, then we could generalize the constants of motion given in Equations (4) and (5) in Equation (42). If the force comes from a potential, Equation (44) turns out to be Equation (45) and it can be satisfied only in the vacuum case or in the case where there is just one body. In these cases, we obtain the constants of motion of Equations (4) and (5) from Equation (42) and we can generalize them in Equation (53), provide that Equation (50) is satisfied.

Then, we see another advantage of the master equation. We define the trajectory and the temporal Equations (Equations (8) and (58)) and we develop a more convenient algorithm for solving the equation of motion.

Finally, we can say that we develop a new formalism of classical mechanics based on Equation (29). We can conclude that the main advantages and disadvantages of our formalism, compared to the two formalisms mentioned in the introduction are the following:

• If the force does not come from a potential but it depends on the position, the formalism works well. This is an advantage compared to the Hamilton-Lagrange’s formalism.

• It includes the friction with the medium, considering a drag force proportional to the square of the velocity. This is also an advantage compared to the Hamilton-Lagrange’s formalism which in this case works only in the one dimensional case [3] .

• It has a more convenient algorithm for solving the equation of motion. This is an advantage compared to the other two formalisms.

• It does not work when there are constraint forces or even if the forces depend explicitly on the time or on the velocities (with the exception of the drag force). This is a disadvantage compared to the Hamilton-Lagrange’s formalism.

Cite this paper

FedericoPetrovich, (2016) A New Formulation of Classical Mechanics—Part 1. Journal of Applied Mathematics and Physics,04,412-431. doi: 10.4236/jamp.2016.42048

References

Appendix

Definition: Let A,. We will say that A is parallel to b () if there exists such that (can be null). If we shall write, while if we shall write.

Note 1: if and, then if and only if.

Note 2: if and only if.

Note 3: for any matrix A (taking).

Remark: Let, and let

Let also, be a base of and orthogonal subspace respec- tively where the dot product is given by

Then, the following conditions are equivalent:

1.

2.

3.

Note 1: we can see in this remark that condition is equivalent to a system of equations.

Note 2: it is easy to find a base of orthogonal subspace. For example if and, we can take and. This holds analogously for B.

Proposition: Let A, with. The following conditions are equivalent:

1.

2.

Proof:

1 2) Since, then there exists such that

On the one hand, this implies that

On the other hand,

Then, this also implies

2 1) On the one hand, since, then there exists such that

This implies

On the other hand, since, then there exists such that

Let. There are two cases, or.

In the first case, since , then . This implies (since) and then

In the second case we have

If we use again that we also have

Since i was arbitrary, then

Therefore

Note 1: if the above proposition holds analogously.

Note 2: if we change by or the above proposition also holds.