Journal of Applied Mathematics and Physics
Vol.2 No.7(2014), Article
ID:47028,9
pages
DOI:10.4236/jamp.2014.27073
Modelling Turbulent Heat Transfer in a Natural Convection Flow
Claudia Zimmermann, Rodion Groll
Center of Applied Space Technology and Microgravity, University of Bremen, Bremen, Germany
Email: groll@zarm.uni-bremen.de
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 March 2014; revised 10 April 2014; accepted 17 April 2014
ABSTRACT
In this paper a numerical study of a turbulent, natural convection problem is performed with a compressible Large-Eddy simulation. In a natural convection the fluid is accelerated by local density differences and a resulting pressure gradient. Directly at the heated walls the temperature distribution is determinate by increasing temperature gradients. In the centre region convective mass exchange is dominant. Density changes due to temperature differences are considered in the numerical model by a compressible coupled model. The obtained numerical results of this study are compared to an analogue experimental setup. The fluid properties profiles, e.g. temperature and velocity, show an asymmetry which is caused by the non-Boussinesq effects of the fluid. The investigated Rayleigh number of this study lies at Ra = 1.58 × 109.
Keywords:Turbulent Natural Convection, Compressible Flow, Large-Eddy Simulation, Heat Transfer

1. Introduction
Convection flows are one of the fundamental problems in fluid dynamics. They play a decisive role in meteorology where they appear as wind caused by solar radiation in the atmosphere. Moreover, they are important in industrial applications, where they are used, to mention just one example, in cooling systems to reduce possible noise exposures and technical failures. Although many theoretical, experimental and numerical investigations have been performed in the past, these flows are not quite understood and they are still of substantial interest. The main focus of this paper lies on a Large-Eddy simulation (LES) of the effective lift due to the occurred convection and the following thermal mixing of the flow. Therefore, a rectangular air-filled container with plane walls is chosen as computational geometry. The vertical side walls of the container are heated isothermally with a constant temperature difference 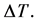 The computational test case is chosen analogously to a comparable experimental test case of Tian and Karayiannis in [1] .
The computational test case is chosen analogously to a comparable experimental test case of Tian and Karayiannis in [1] .
2. Test Case Configuration
To investigate the natural convection in the simulation, the computational test case is built of a rectangular, air-filled, enclosed container, with a length (L) of 0.75 m, a height (H) of 0.75 m and a depth (D) of 1.5 m. A scheme of the computational test case is displayed in Figure 1, left picture.
The vertical sidewalls of the setup are heated differently, but homogeneously with a constant temperature difference of 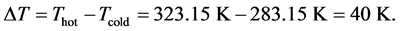 The vertical orientation of the heated walls implies a quasi-steady state flow in the setup. Due to a non-slip condition, the velocity field at all walls is zero
The vertical orientation of the heated walls implies a quasi-steady state flow in the setup. Due to a non-slip condition, the velocity field at all walls is zero . The experimental test case consists of highly conducting sidewalls [1] . This boundary condition is modelled in the simulation by an ideal linear temperature distribution between the hot and cold wall. Also an adiabatic temperature condition is analysed. The convection cell can be described by the parameters of the Rayleigh number Ra, the Prandtl number Pr, the Nusselt number Nu and its aspect ratios
. The experimental test case consists of highly conducting sidewalls [1] . This boundary condition is modelled in the simulation by an ideal linear temperature distribution between the hot and cold wall. Also an adiabatic temperature condition is analysed. The convection cell can be described by the parameters of the Rayleigh number Ra, the Prandtl number Pr, the Nusselt number Nu and its aspect ratios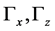 . These parameters are defined as
. These parameters are defined as
 (1)
(1)
where g is the gravitational acceleration, 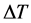 the temperature difference between the horizontal walls,
the temperature difference between the horizontal walls, 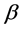 the coefficient of thermal expansion, H the height of the container,
the coefficient of thermal expansion, H the height of the container,  the thermal diffusivity,
the thermal diffusivity, 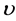 the kinematic viscosity and
the kinematic viscosity and  the temperature gradient directly at the heated walls (index w). The Nusselt number characterises the heat flux in the container. All parameters in Equation (1) correspond to the mean temperature field
the temperature gradient directly at the heated walls (index w). The Nusselt number characterises the heat flux in the container. All parameters in Equation (1) correspond to the mean temperature field 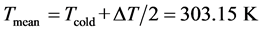 between both heated walls of the setup. The internal temperature field in the container is chosen as the mean temperature field,
between both heated walls of the setup. The internal temperature field in the container is chosen as the mean temperature field, 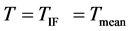 , analogously to the experiment in [1] . If the fluid exceeds a critical value of the Rayleigh-number, it starts moving, controlled by the temperature difference of the vertical, heated walls. The Prandtl number lies in this study at Pr = 0.71. The simulation assumes a nonBoussinesq fluid, consequently, temperature dependent fluid properties are calculated by the Sutherland model as stated in [2] . The computational geometry consists of a Cartesian block-structured mesh with 27 blocks. A scheme of the mesh can be seen in Figure 1, right picture. This mesh partition enables an exterior zone where a finer resolution can easily be chosen independently of the other blocks. Directly at the walls the mesh is clustered and the cell ratios decrease to the walls. In this way, all relevant turbulent scales can be resolved and no wall functions have to be considered. In the middle of the geometry, large scales of the flow are dominant. Thus, the mesh can have a coarser resolution in this region than close to the walls. The final mesh consists of
, analogously to the experiment in [1] . If the fluid exceeds a critical value of the Rayleigh-number, it starts moving, controlled by the temperature difference of the vertical, heated walls. The Prandtl number lies in this study at Pr = 0.71. The simulation assumes a nonBoussinesq fluid, consequently, temperature dependent fluid properties are calculated by the Sutherland model as stated in [2] . The computational geometry consists of a Cartesian block-structured mesh with 27 blocks. A scheme of the mesh can be seen in Figure 1, right picture. This mesh partition enables an exterior zone where a finer resolution can easily be chosen independently of the other blocks. Directly at the walls the mesh is clustered and the cell ratios decrease to the walls. In this way, all relevant turbulent scales can be resolved and no wall functions have to be considered. In the middle of the geometry, large scales of the flow are dominant. Thus, the mesh can have a coarser resolution in this region than close to the walls. The final mesh consists of
 cells in (x,y,z)-direction. The first grid point is located at
cells in (x,y,z)-direction. The first grid point is located at  in vertical distance to the hot, respectively cold, wall. To analyse possible grid dependencies, additionally to the 3D simulation also a 2D simulation is performed with a mesh resolution of
in vertical distance to the hot, respectively cold, wall. To analyse possible grid dependencies, additionally to the 3D simulation also a 2D simulation is performed with a mesh resolution of  cells in (x,y)-direction. The cells are equally spaced over the plane. The first grid point is located at
cells in (x,y)-direction. The cells are equally spaced over the plane. The first grid point is located at 
in vertical distance to the hot, respectively cold, wall. The non-dimensional distance from the wall 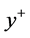 is given by
is given by
 (2)
(2)
where  is the wall shear rate,
is the wall shear rate, 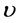 the kinematic viscosity and
the kinematic viscosity and ![]() dynamic viscosity.
dynamic viscosity.  marks the velocity gradient directly at the wall. Table 1 lists values of
marks the velocity gradient directly at the wall. Table 1 lists values of 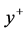 estimated in the first cell midpoint
estimated in the first cell midpoint 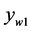 in the full turbulent flow for both simulation types and both temperature boundary conditions.
in the full turbulent flow for both simulation types and both temperature boundary conditions.
The different values between the simulation types are caused by different velocities close to the heated walls.
3. Governing Equations
Thermally driven flow in the setup is described as a turbulent compressible problem. “Compressible” referred in this case to density changes in the fluid due to temperature differences and not to a definition in terms of the Mach number. The turbulent, 3-dimensional flow field is calculated using a transient LES with the open-source


Figure 1. Left: Configuration of the computational test case. Right: Computational mesh resolution with cells.
cells.
Table 1. Temperature boundary conditions and values of the non-dimensional wall distance y+.
simulation tool OpenFOAM®. In a LES the flow is separated in large and small scales, the so-called subgrid scales (marked by index “sgs” in the following). The large scales are solved directly on the discretisation grid, while the subgrid scales are modelled with an applicable turbulence model, which is in this study the so-called model of Fureby [3] . This model is based on the compressible Smagorinsky model. It assumes a thermodynamic ideal gas
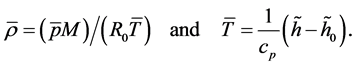 (3)
(3)
For the LES a space-time variable is separated and subsequent filtered as follows
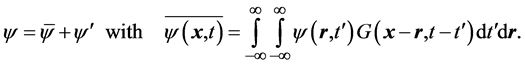 (4)
(4)
Additionally, the dense weighted Favre-filtering of Vreman [4] is used
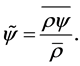 (5)
(5)
Hence, the governing equations are
Ÿ Compressible conservation of mass
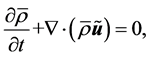 (6)
(6)
Ÿ Compressible conservation of momentum
 (7)
(7)
Ÿ Compressible conservation of enthalpy
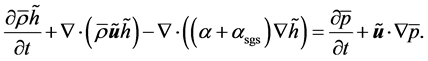 (8)
(8)
Additional force terms, which model the natural convection in the turbulent flow as in [5] [6] or a Boussinesq-approximation as in [7] [8] are not included in equation (7). The subgrid-scale dynamic viscosity  and the subgrid-scale thermal diffusivity
and the subgrid-scale thermal diffusivity  are defined as
are defined as
 (9)
(9)
The turbulent Prandtl number  is taken with
is taken with  according to [6] [9] [10] .
according to [6] [9] [10] .  is the subgridscale turbulent kinematic energy which is defined as
is the subgridscale turbulent kinematic energy which is defined as
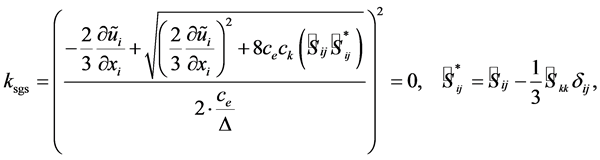 (10)
(10)
with the deviatoric part of the strain rate tensor  the filtered strain rate tensor
the filtered strain rate tensor
 (11)
(11)
and two model coefficients, 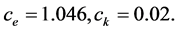 The temperature-dependence of the fluid properties is described by the Sutherland model [2] . For ideal gases it gives a relation between the dynamic viscosity
The temperature-dependence of the fluid properties is described by the Sutherland model [2] . For ideal gases it gives a relation between the dynamic viscosity  and the absolute temperature
and the absolute temperature 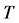
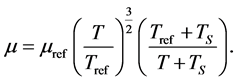 (12)
(12)
 is a reference dynamic viscosity at a reference temperature
is a reference dynamic viscosity at a reference temperature 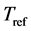 and
and 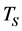 is the so-called Sutherland temperature. In this study these coefficients are chosen as
is the so-called Sutherland temperature. In this study these coefficients are chosen as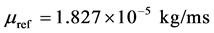 ,
,  and
and

4. Results
4.1. Temperature Profile between the Heated Walls
The flow movement of the convection is initialised by the temperature difference between the vertical walls. Thus, the temperature profile is one important aspect to understand the dynamic of the flow. Figure 2 displays the typical temperature and vertical velocity profile at the xy-midplane for a natural convection in the investigated setup. Near to the vertical walls, the temperature and vertical velocity can be described by a linear law. This region is called the inner layer of the boundary layer. In the following, the time-averaged temperature profile is estimated between the heated walls at the xy-midplane at ,
, 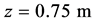 for three different heights,
for three different heights,
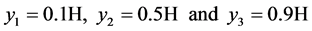 . The time-averaged results of the 3D and 2D simulation are plotted against the experimental data of Tian and Karayiannis [1] in Figure 3.
. The time-averaged results of the 3D and 2D simulation are plotted against the experimental data of Tian and Karayiannis [1] in Figure 3.
The thermal boundary layer near the heated walls and a variation of its thickness along the heated walls can clearly be seen. Further, a dependence on the particular boundary condition is visible. The boundary layer increases in the clockwise flow direction. Steep temperature gradients appear, before they reach their minimum at ca. 0.03 m afar from the hot wall (respectively 0.73 m from the cold wall), where the bulk region begins. Here, the temperature is almost stationary and almost equal to the mean temperature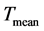 . The simulation profiles are not formed anti-symmetrically as in the experiment, but even asymmetrically. According to the study of Gifford in [11] , the anti-symmetrical profile vanishes for a non-Boussinesq-approximation. At midheight, all simulations approximate well the bulk temperature of the measured data. In vicinity of both horizontal walls the adiabatic results deviate significantly from the experiment, due to the adiabatic condition. Adiabatic walls entail no heat flux which implies lower temperatures. According to Tian and Karayiannis in [1] , the vertical thermal boundary layer of an experiment with an adiabatic boundary condition is thicker than the boundary layer of one with a conducting condition. This is fulfilled in the numerical results for the adiabatic case compared to the data of [1] . One exception is position
. The simulation profiles are not formed anti-symmetrically as in the experiment, but even asymmetrically. According to the study of Gifford in [11] , the anti-symmetrical profile vanishes for a non-Boussinesq-approximation. At midheight, all simulations approximate well the bulk temperature of the measured data. In vicinity of both horizontal walls the adiabatic results deviate significantly from the experiment, due to the adiabatic condition. Adiabatic walls entail no heat flux which implies lower temperatures. According to Tian and Karayiannis in [1] , the vertical thermal boundary layer of an experiment with an adiabatic boundary condition is thicker than the boundary layer of one with a conducting condition. This is fulfilled in the numerical results for the adiabatic case compared to the data of [1] . One exception is position 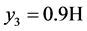 at the hot wall. This aspect could be a possible hint at shifted
at the hot wall. This aspect could be a possible hint at shifted
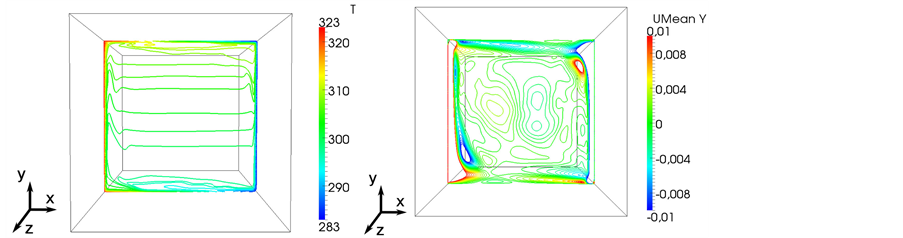
Figure 2. Instantaneous temperature (left) and vertical velocity (right) profile between the heated walls, linear temperature condition.




Figure 3. Time-averaged temperature profile at the vertical xy-midplane along the horizontal axis, at x = 0.75 m, z = 0.75 m and different heights. Top: Adiabatic bc. Bottom: Linear bc. Detailed plot of the hot/cold wall. In all pictures: y1 = 0.1H (blue), y2 = 0.5H (red) and y3 = 0.9H (black), − (solid line): 3D, − − − (dashed line): 2D.  study Tian and Karayiannis [1] , Ra = 1.58 × 109.
study Tian and Karayiannis [1] , Ra = 1.58 × 109.
circulation zones compared to the experiment. The 2D plot shows only slight deviations to the 3D plot. The linear results approximate the experimental data closer than the adiabatic results, due to the similar boundary condition. The results of the 2D-simulation lie even closer to the experimental data than the results of the 3D simulation.
4.2. Nusselt Number Profile along the Heated Walls
Besides the temperature distribution, also values of the Nusselt number are evaluated along the isothermal heated walls and plotted in Figure 4. With Equation (1) the heat flux is defined positive in direction from the hot wall into the container and in direction to the cold wall (respectively from the bottom to the top wall). The adiabatic 3D simulation matches at midheight of the hot wall exactly with the values of [1] . The cold wall value is slightly lower than in [1] . The time-averaged values at midheight deviate at most about 5% from the experiment, which can be neglected. From midheight on, the values underrun the experimental results due to lower temperature gradients as seen before in Figure 3. The 2D results display an equal tendency as the 3D ones and show only differences in vicinity to the heated walls. The time-averaged results of both simulation types of the linear case reveal an analogue profile to [1] , as it was expected due to the similar boundary conditions. The 3D case presents higher results than the 2D case, which is founded in steeper temperature gradients. The data of the

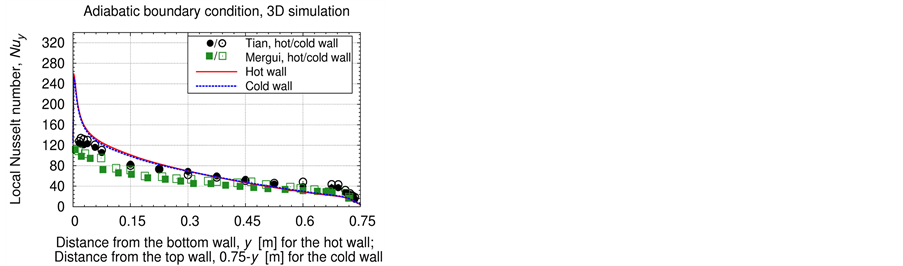


Figure 4. Time-averaged profile of the local Nusselt number along the heated walls. Top: Adiabatic bc. Bottom: Linear bc. Left: 3D simulation. Right: 2D simulation. In each picture: − (red solid line): hot wall, − − − (blue dashed line): cold wall. Study Tian and Karayiannis [1] : ●: hot wall,  cold wall, Ra = 1.58 × 109. Study Mergui, Penot and Tuhault [12] : ∎ : hot wall, □ : cold wall, Ra = 1.34 × 109.
cold wall, Ra = 1.58 × 109. Study Mergui, Penot and Tuhault [12] : ∎ : hot wall, □ : cold wall, Ra = 1.34 × 109.
3D case are slightly lower at the hot wall than at the cold one. But the values at midheight deviate in both simulations significantly from the data in [1] , of about at most 20%. This might possibly be caused by lower temperature gradients. The numerical data approximate well the numerical study of Mergui, Penot and Tuhault [12] .
4.3. Vertical Velocity Profile between the Heated Walls
Figure 2 shows a snapshot of the instantaneous mean velocity distribution at the xy-midplane in the container for the linear boundary condition. The plot reveals an exterior circulation zone as well as an interior one. Both circulations are reversed to each other. Furthermore, smaller circulations appear additionally in the left bottom and top right corner as well as top left and bottom right corner. In this section, the time-averaged vertical velocity profile at the xy-midplane between the temperatured walls is investigated and plotted in Figure 5. The profiles are estimated at the same positions as the temperature profiles before in Figure 3. For a better demonstration a constant was added to the results of each height, which are: 
As in the temperature profile, a clockwise circulation direction and an increase of the boundary layer along the heated walls in flow direction are visible. The boundary layer reaches its maximum width at the hot wall at height  (respectively at the cold wall at height
(respectively at the cold wall at height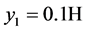 ). The thermal boundary layer is smaller than the velocity boundary layer. As in [1] , negative values appear between the inner and outer layer of the profile in the simulation results which indicate possibly a reverse flow. The vertical velocity component reveals at every height high peak values close to the vertical, heated walls. Minor decreases with negative values can be noticed outside the boundary layer at the hot wall (vice versa at the cold wall). According to [1] , this decrease/ increase might indicate two further possible clockwise circulation zones. The adiabatic profile shows a slightly smaller boundary layer than in the experiment, as it was expected. The peak values are located closer to the heated walls and lie beneath the experimental ones. No significant differences arise between the 2D and 3D simulation results. The profiles of the linear boundary case approximate well the results of [1] . Due to the different temperature conditions at the horizontal walls between the simulation and experiment of [1] , the peak values of the 3D and 2D simulation are higher than in the experimental study.
). The thermal boundary layer is smaller than the velocity boundary layer. As in [1] , negative values appear between the inner and outer layer of the profile in the simulation results which indicate possibly a reverse flow. The vertical velocity component reveals at every height high peak values close to the vertical, heated walls. Minor decreases with negative values can be noticed outside the boundary layer at the hot wall (vice versa at the cold wall). According to [1] , this decrease/ increase might indicate two further possible clockwise circulation zones. The adiabatic profile shows a slightly smaller boundary layer than in the experiment, as it was expected. The peak values are located closer to the heated walls and lie beneath the experimental ones. No significant differences arise between the 2D and 3D simulation results. The profiles of the linear boundary case approximate well the results of [1] . Due to the different temperature conditions at the horizontal walls between the simulation and experiment of [1] , the peak values of the 3D and 2D simulation are higher than in the experimental study.
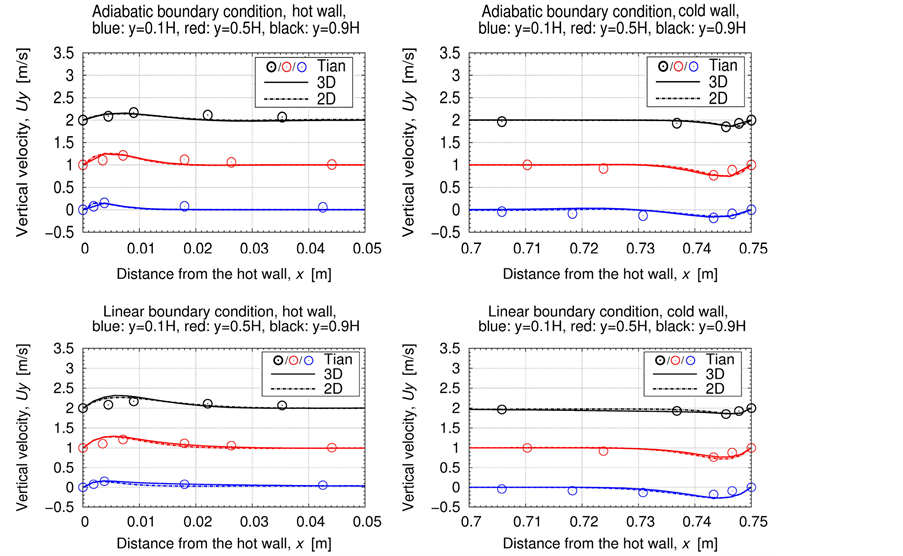
Figure 5. Time-averaged vertical velocity profile at the xy-midplane, at x = 0.75 m, z = 0.75 m and different heights. Top: Adiabatic bc. Bottom: Linear bc. Detailed plot of the hot/cold wall. In all pictures: y1 = 0.1H (blue), y2 = 0.5H (red) and y3 = 0.9H (black), − (solid line): 3D, − − − (dashed line): 2D.  study Tian and Karayiannis [1] , Ra = 1.58 × 109.
study Tian and Karayiannis [1] , Ra = 1.58 × 109.
4.4. Wall Shear Stress along the Heated Walls
According to Tian and Karayiannis in [1] , a cubic law can be assumed for the velocity profile in the outer region of the inner layer. Therefore, the shear stress profile is described as
 (13)
(13)
with the gradient of the vertical velocity component directly at the heated walls (index w) and a depending dynamic viscosity . Besides the experimental data of [1] also another experimental study of King [13] is compared to the numerical data of this study in Figure 6.
. Besides the experimental data of [1] also another experimental study of King [13] is compared to the numerical data of this study in Figure 6.
As Figure 6 shows, the time-averaged shear stress rises, analogously to the velocity, along the vertical, heated walls to its peak value and back to zero in the corners. The results of [1] reveal an asymmetry in the corner regions. The data of King [13] reveals higher values than in the study of Tian and Karayiannis [1] , which are possibly caused by a higher investigated Rayleigh number of King [13] according to [1] . The simulation profiles show an asymmetrical form, which is founded in the asymmetrical velocity profile. All simulations reveal negative values in the top hot and bottom cold corner which indicate anti-clockwise vortex regions as mentioned in [1] . The values along the heated walls in this study are higher than the data of [1] , due to higher velocity gradients and higher dynamic viscosity values. The high values of this study approximate rather the data of King [13] than of Tian and Karayiannis [1] .
5. Conclusion
A non-Boussinesq, compressible LES was performed for a turbulent, natural convection in an air-filled enclosed container with vertical heated walls. The results were compared to an analogue experimental setup of Tian and Karayiannis [1] . In the experiment, the setup consisted of conducting later walls, while in the numerical simulation two different related boundary conditions were tested. Additionally to the 3-dimensional simulations,
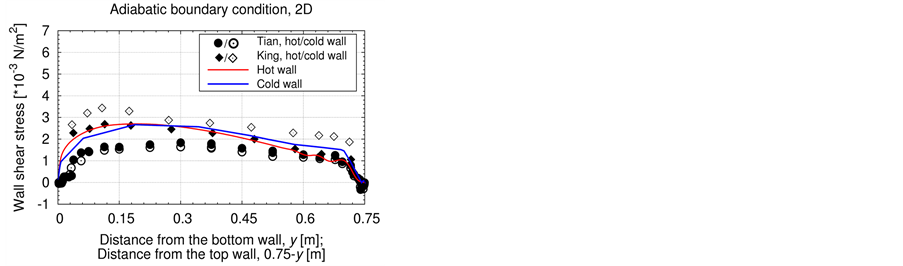


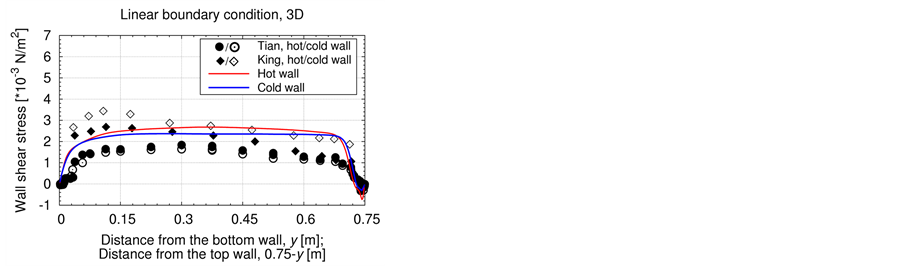
Figure 6. Time-averaged wall shear stress profile along the heated walls. Top: Adiabatic bc. Bottom: Linear bc. Left: 3D simulation. Right: 2D simulation. In all pictures: − (red solid line): hot wall, − (blue solid line): cold wall. Study Tian and Karayiannis [1] :  hot wall,
hot wall,  cold wall, Ra = 1.58 × 109. Study King [13] : ♦: hot wall, ◊: cold wall, Ra = 4.5 × 109.
cold wall, Ra = 1.58 × 109. Study King [13] : ♦: hot wall, ◊: cold wall, Ra = 4.5 × 109.
2-dimensional simulations were executed to investigate possible grid dependencies. Taking the different boundary conditions and the non-Boussinesq fluid assumption of the computational study into consideration, the results of the investigated fluid properties in all 3-dimensional simulations approximated well the experimental results of [1] . The simulation data showed the same profile tendencies as in the experiment [1] . The results of the 2- and 3-dimensional simulations revealed in most cases similar results and only small deviations to each other which appeared mainly in vicinity to the heated walls. These deviations have to be further investigated in future studies to find an additional explanation as the one of grid dependencies. Summarising, the presented LES is very qualified to model the flow structures and fluid properties profiles of a turbulent, natural convection flow in the investigated configuration of a rectangular container where the vertical walls are heated.
Acknowledgements
The authors wish to thank the North-German Supercomputing Alliance (HLRN) for providing their hardware during the numerical simulations of this study.
References
- Tian, Y.S. and Karayiannis, T.G. (2000) Low Turbulence Natural Convection in an Air Filled Square Cavity, Part I: The Thermal and Fluid Flow Fields. International Journal of Heat and Mass Transfer, 43, 849-866. http://dx.doi.org/10.1016/S0017-9310(99)00199-4
- Sutherland, W. (1893) The Viscosity of Gases and Molecular Force. Philosophical Magazine, Series 5, 36, 507-531.http://dx.doi.org/10.1080/14786449308620508
- Fureby, C. (1996) On Subgrid Scale Modeling in Large Eddy Simulations of Compressible Fluid Flow. Physics of Fluids, 8, 1301-1311. http://dx.doi.org/10.1063/1.868900
- Vreman, B. (1995) Direct and Large-Eddy Simulation of the Compressible Turbulent Mixing Layer. Ph.D. Thesis, University of Twente, Enschede.
- Kenjeres, S. and Hanjalic, K. (1999) Transient Analysis of Rayleigh-Bénard Convection with a RANS Model, International Journal of Heat and Fluid Flow, 20, 329-340. http://dx.doi.org/10.1016/S0142-727X(99)00007-7
- Sergent, A., Joubert, P. and Quéré, P. Le (2003) Development of a Local Subgrid Diffusivity Model for Large-Eddy Simulation of Buoyancy Driven Flows: Application to a Square Differentially Heated Cavity. Numerical Heat Transfer, Part A: Applications, 44, 789-810.
- Shishkina, O. and Wagner, C. (2008) Analysis of Sheet-Like Thermal Plumes in Turbulent Rayleigh-Bénard Convection. Journal of Fluid Mechanics, 599, 383-404. http://dx.doi.org/10.1017/S002211200800013X
- Shishkina, O. and Thess, A. (2009) Mean Temperature Profiles in Turbulent Rayleigh-Bénard Convection of Water. Journal of Fluid Mechanics, 633, 449-460. http://dx.doi.org/10.1017/S0022112009990528
- Kosovic, B., Pullin, D.I. and Samtaney, R. (2002) Subgrid-Scale Modeling for Large-Eddy Simulations of Compressible Turbulence, Physics of Fluids, 14, 1511-1522. http://dx.doi.org/10.1063/1.1458006
- Erlebacher, G., Hussaini, M.Y., Speziale, C.G. and Zang, T.A. (1992) Toward the Large-Eddy Simulation of Compressible Turbulent Flows. Journal of Fluid Mechanics, 238, 155-185. http://dx.doi.org/10.1017/S0022112092001678
- Gifford, W.A. (1991) Natural Convection in a Square Cavity without the Boussinesq-Approximation. 49th Annual Technical Conference-ANTEC’91, Montreal, 5-9 May 1991, 2448-2454.
- Mergui, S., Penot, F. and Tuhault, J.H. (1993) Experimental Natural Convection in an Air-Filled Square Cavity at . In: Henkes, R.A.W.M. and Hoogendoorn, C.J., Eds., Turbulent Natural Convection in Enclosures—A Computational and Experimental Benchmark Study, Proceedings of the Eurotherm Seminar no 22, Editions Européennes Thermique et Industrie, Paris, 9-108.
- King, K.J. (1989) Turbulent Natural Convection in Rectangular Air Cavities. Ph.D. Thesis, Queen Mary and Westfield College, University of London, London, UK.


