Theoretical Economics Letters
Vol.08 No.11(2018), Article ID:86553,21 pages
10.4236/tel.2018.811144
Integration of GDP and FDI in Economies at Different Stages of Growth
Shalini Talwar*, Shaila Srivastava
K J Somaiya Institute of Management Studies & Research, Vidyanagar, Vidyavihar (East) Mumbai, India

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 22, 2018; Accepted: August 6, 2018; Published: August 9, 2018
ABSTRACT
The objective of this study is to analyze the relationship between FDI and GDP for countries representing developed, developing and underdeveloped economies around the world. The countries identified for the purpose are Bhutan, Ethiopia, India, Brazil, USA and UK. Johansen cointegration test reveals that long-run equilibrium relationship between the two variables exists for Ethiopia, India and UK only. The VEC model shows no related short-run causality for any of these three countries. The study has implications in terms of policy decisions. Using FDI to boost GDP growth rate in the short-run is not an effective option for any country under the study. Since the vector error correction (VEC) model suggests that the two variables have a statistically significant adjustment mechanism for India, the study concludes that India can use FDI to leverage her long-term GDP. No evidence of link between the state of development of economy and integration of FDI and GDP is found by the study.
Keywords:
Cointegration Test, Foreign Direct Investment, Granger Causality Test, Gross Domestic Product, Unit Root Test, Vector Error Correction Model (VECM)

1. Introduction
For every country, the goal of development-oriented policies is to alleviate poverty and improve the standard of living of its people. To meet this objective, governments need formulate policies driven by the strategy of sustainable economic growth and investment in people. However, given the issue of resource constraint, countries cannot achieve this goal by utilizing their internal funds alone. They need to raise funds from sources outside their domestic economy. There are multiple sources of foreign funding that a country can use. FDI (Foreign direct investments) is one such source that countries across the world are trying to use to power their growth, measured in terms of GDP (Gross domestic product). It is a common understanding that countries should allow foreign inflows in the form of FDI for financing projects and programmes that propel growth. Many countries are pursuing highly liberal FDI-related policies. Currently, all types of economies are working towards attracting FDI flows to their countries and to achieve this, the concerned governments are formulating accommodative policies and endeavoring to improve their ranking in the Ease of Doing Business report of World Bank (http://www.doingbusiness.org/rankings).
The question is: are all these efforts of boosting FDI really pushing up growth? Though existing research has indicated that there is a linkage between FDI and GDP, yet there is a debate as to how much is the impact of FDI on GDP or vice versa, in the context of different categories of economies, namely, underdeveloped, developing and developed.
In this paper, the authors have tried to evaluate the causality and stable long-run linear relationship between GDP growth rate (GDPGR) and FDI over a period of thirty years using econometric tests for six countries, namely, Bhutan, Ethiopia, India, Brazil, USA and UK. Of the selected countries, Bhutan and Ethiopia represent the underdeveloped; India and Brazil represent the developing and USA and UK represent the developed economies. This categorization is important because the current study also seeks to verify the general impression of FDIs being more critical for the growth of the underdeveloped and developing economies as compared to the developed economies.
The FDI as percentage of GDP has grown from zero percent in 1987 to little less than half a percent in 2016 for Bhutan. GDP growth rate has varied over the years for Bhutan showing no steady trend of increase or decrease. In case of Ethiopia, FDI as percentage of GDP increased from 0 percent to 5.5 percent during the period under the study, with no particular trend in GDP growth. In case of Brazil and India, FDI as percentage of GDP increased from 0.4 percent to 4.35 percent, 0.08 percent to 1.96 percent respectively during the period under the study. During the same period, Brazil has recorded very low growth in GDP whereas India’s GDP growth has been largely steady. FDI as percentage of GDP was 11.07 percent for UK and 2.57 percent for US in 2016. The GDP growth rate was 1.5 percent for US and 1.8 percent for UK in 2016.
The choice of countries is completely guided by the availability of data in the case of the underdeveloped economies. In the case of the developing economies, two of the BRICS countries have been chosen deliberately. For the representation of the developed economies, UK and USA have chosen as they have been the leading economies in the world since past many decades. An in-depth statistical inference of the causality between foreign direct investment and economic growth is critically important from a policy point of view.
The study of causality in the context of economic growth has been quite popular with researchers. The direction of causality between financial development and economic growth in Zimbabwe and Malawi was examined in a study using the Johansen and Juselius and the Hsiao’s tests. The results of the tests revealed there was a distinct bi-directional causality between the two variables for Malawi [1] . Causal relationship between financial development and economic growth was examined in a study that presented a simple endogenous growth model to demonstrate the role of financial development in economic growth [2] . Another study tested the effects of population growth, openness and economic freedom on economic growth as well as the causality between economic freedom and economic growth [3] . Granger causality test confirmed the direction of causality from economic freedom to economic growth. Many other studies have also used econometric tests to evaluate various economic indicators and their relationship.
The findings of the study reveal the absence of short-run causality running from FDI to GDPGR for all the countries under the study. Further, the analysis has shown that long-run causality runs from FDI to GDP growth rate for India. This has key implications for policy makers in India looking to boost short- and long-run GDP. In addition to the above findings, this study has also highlighted the fact that there is no connection between the state of development of economies and their FDI/GDPGR causal relationship.
To the best of the knowledge of the authors, this is one of the very few studies undertaken to investigate the potentially causal relationship between FDI flows and GDP growth rate during the 1987-2016 period for the set of countries used by this study from the perspective of analyzing if there can be a generalization that FDI is more effective to power GDP growth rate for a particular type of economy.
The rest of the paper is organized as follows: the second section presents the literature reviewed by the author in brief. The third section gives the data description followed by the section on methodology used in the study. The fifth section focuses on analysis and discussion of results and the sixth section presents summary and conclusion. The seventh section discusses the limitations of the study and highlights the opportunities for future research.
2. Literature Review
Since economic indicators have policy implications, they have been widely researched across economies and rich literature is available to provide the right context to take the research in the field forward. The researchers have reviewed the related literature from the perspective of drivers of economic growth, importance of FDI in economies of different types and the linkages between FDI and GDP growth rate.
A study on the impact of FDI flows in South Africa on the current account balance found that since 2004, the dependence of the South African economy on capital inflows had increased to the extent that net dividend payments on FDI flows made up 36 per cent of the current account deficit for the period from 2004 through 2012 [4] .
A study examined the impact of the drivers of economic growth in developing countries and found that the growth rate of per capita GDP was linearly dependent on technological progress, gross capital formation, the initial level of output per capita, labor productivity growth and human capital formation [5] .
Another researcher [6] analyzed the effects of foreign aid and FDI on economic growth in middle income and low income African countries by employing a dynamic Generalized Method of Moments (GMM) model and found that the middle income countries tended to have more impact on their economic growth from FDI as compare to low income countries. Another study [7] based on Albania, revealed a strong positive relationship between the FDI inflows and the GDP for a period from 1995 to 2012. A recent study [8] examined the relationship between foreign direct investment (FDI) and economic growth in the five BRICS economies over the period 1989-2012 and found that FDI and economic growth were cointegrated at the panel level, indicating the presence of a long-term equilibrium relationship between them.
A study [9] revealed that FDI exerted an exogenous positive impact on economic growth. Further, FDI tended to have a larger impact on economic growth when there was sufficient absorptive capacity including R&D indicators and when occurring in technologically more advanced transition economies. In another recent study [10] the authors applied meta-analysis to understand whether FDI-related productivity spillovers at the firm had been of sufficient size to affect growth at the aggregate level in China. The study found the effect of FDI on Chinese economic growth to be quite small. Yet another study [11] found that FDI facilitated growth by enhancing physical and human capital accumulation but also had negative effects as it resulted in interregional growth gap. A study [12] investigated the impact of foreign direct investment (FDI), foreign aid and remittances on the economic growth of selected countries and found FDI to be significant only in the case of African countries.
Another study [13] applied Ng-Perron and DF-GLS unit root tests to determine the level of integration as well as the autoregressive distributed lag (ARDL) method to identify the long-run relationship between exports and inward foreign direct investment (FDI) on economic development in Greece and found long-run relationship between these variables. A study [14] based on Central and Eastern European countries found that FDI exerted a positive influence on growth, employment rate and income to the state budget, confirming the existence of the causal relation between FDI and economic growth.
Another study [15] investigated FDI-growth nexus for 16 developing countries of Latin American and the Caribbean countries during the last three decades. Toda-Yamamoto and Dolado-Lutkepohl (TYDL) methodology to test causality found evidence of unidirectional causality from growth to FDI for all countries except Bolivia, Colombia, Costa Rica, Dominican Republic, Ecuador, El Salvador, Guatemala, and Jamaica. Bidirectional causality was found for Argentina, Brazil, Mexico, Peru and Venezuela.
3. Data Description
The current study attempts to diagnose the causal relationship between FDI and GDP growth rate in both short and long run for six countries, namely, Bhutan and Ethiopia representing underdeveloped economies, India and Brazil representing developing economies and USA and UK representing developed economies.
The data for GDP growth rate and total net inflows for FDI used in this study is the annual time series at constant prices for three decades from 1987 through 2016. The data has been obtained from the relevant World Bank, International Monetary Fund, World Economic Outlook and World Investment reports.
The data used for the study is given in Table 1 and Table 2.
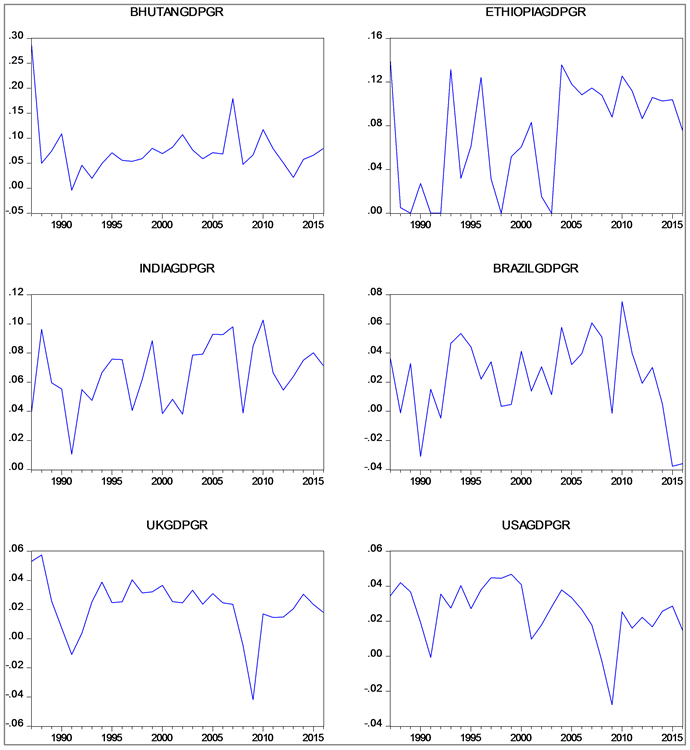
Descriptive statistics of the data series under the study is presented in Table 3 and the time series plot of the data under the study is given in Figure 1 and Figure 2. Mean, median standard deviation, minimum, maximum, skewness kurtosis and Jarque-bera values of dependent and independent variables are calculated for all six countries. Mean, median and standard deviation reveal the statistical nature of the time series under the study. Jarque-Bera statistic indicates the distribution of the series and tests the null hypothesis that data is normally distributed.
Table 1. Data for GDP for selected countries.
Source: World Bank data.
Table 2. Data for FDI for selected countries.
Source: World Bank data.
Table 3. Descriptive statistics for GDP growth rate and FDI for selected countries.
Source: Based on authors’ calculations.
Figure 1. Time series plot of GDP Growth rate for selected countries. Source: Based on authors’ calculations.
Starting with dependent variable, GDPGR, Bhutan has highest mean growth rate (0.075) and UK has least mean growth rate (0.022) amongst the countries
Figure 2. Time series plot of FDI for selected countries. Source: Based on authors’ calculations.
under the study. The variability in growth rate of GDP has also been maximum for Bhutan, as measured by standard deviation. In case of FDI related data, the average is highest for UK (0.038) and minimum for Bhutan (0.008) amongst the countries under the study.
Probability values of Jarque-Bera statistics in Table 3 confirm that the null of normal distribution cannot be rejected for any the GDPGR and FDI data of any country except both for Bhutan and UK and GDPGR at 5% level of significance. Thus, the variables are largely normally distributed.
4. Methodology
To achieve the objectives of the study, some preliminary statistical analysis has been performed on the time series under investigation. These initial steps include the use of ordinary least square regression to evaluate the dependency relationship among the two variables and Augmented Dickey Fuller unit root test to check the series for stationarity. Thereafter, Johansen’s cointegration test has been applied to all data series to assess the existence of long-run equilibrium relationship and to determine the subsequent test structure, such as a VAR or a VEC testing framework. Further, Granger causality test is applied to the data to detect the existence of unidirectional, bidirectional or no causality between GDP and FDI for each of the country under the study. A brief description of all tests used in the study is given in this section.
4.1. Ordinary Least Squares Method (OLS)
Ordinary least square regression has been performed in EViews with GDPGR as the dependent variable and FDI as the independent variable. The F-statistic in the regression output is used to evaluate the fit of the proposed linear model. The hypothesis tested here is that there is no relationship between Foreign Direct Investment (FDI) and Economic Growth in terms of GDP growth rate.
The null hypothesis is rejected on the basis of the p-value for the F-statistic being less than the significance level of 5percent to conclude that the proposed model provides a better fit than the intercept-only model. Further, R-squared has been used to estimate of the strength of the relationship between the two variables.
The linear regression equation proposed in the study is expressed as follows:
(1)
where, c(1) is the coefficient of regression. It indicates how a unit change in the independent variable (FDI) affects the dependent variable (GDPGR). c(2) is the non-random or the structural component. It is called constant or intercept. c(3) represents the “noise” or error term. The error term is incorporated in the equation to take into account other factors that may influence GDPGR.
The validity or strength of the OLS method depends on the accuracy of its assumptions. In this study, the Gauss-Markov assumptions used are:
1) That the dependent and independent variables (GDPGR and FDI) are linearly co-related,
2) The estimators, c(1) and c(2) are unbiased with an expected value of zero i.e., E (C(3)) = 0, which implies that on average the errors cancel each other.
OLS regression analysis can only establish the dependence of either GDPGR on FDI or vice versa; it does not necessarily imply direction of causation. With the result, Granger causality has been applied to take the analysis further.
4.2. Unit Root Test
Before applying the Granger causality Test, unit root test has been run to test the nature of the data. Augmented Dickey Duller (ADF) [16] ; [17] has been used for the purpose. The objective of this test is to empirically examine THE presence of unit root in the data that can make the data series non-stationary. The ADF test specifications include the intercept and the deterministic time trend variable. The Schwarz information criterion (SIC) is used for the lag length selection.
ADF tests the null hypothesis of unit root against the alternative hypothesis of stationarity and the null is rejected on the basis of low p-value (less than 0.05) for the test statistic thus computed. The ADF test assumes that a nonstationary process has infinite memory and tends to behave like AR (1) process with ρ = 1. ADF test examines if ρ = 1.
Mathematically:
(2)
For Equation (2), the hypothesis tested is if . The test uses the modified critical values tabulated in MacKinnon table. The lagged terms of are also included in the regression to get the white noise.
4.3. Granger Causality Test
Granger causality test [18] ; [19] is used to infer causal relationship between data series. Granger causality tests the null hypothesis of “x does not granger cause y” and “y does not granger cause x”. The null hypothesis is rejected on the basis of low p-value (less than 0.05) for the test statistic thus computed. If a series granger causes the other, it implies that the variable granger causing the other variable can be modeled to generate a more accurate prediction of the caused variable.
Though, FDI and GDPGR can be interlinked and co-related through various channels, the existence and direction of causation needs to be ascertained for the period and the countries under the study. For this reason, Granger causality test is carried out on FDI and GDPGR series. Since Granger causality test can be performed only on stationary data, log values of all data series have been used for testing causality.
Granger test is implemented by running the following regression [20] :
(3)
(4)
where, k represents the optimal lag order; d represents the maximal order of integration of the variables in the system; and represent the error term.
4.4. Johansen Cointegration Test
Johansen cointegration test [21] has been used in the current study to analyze whether there is any long-term relationship between the two variables for all the countries selected for the purpose of the study. Cointegration implies that even though individual data series under empirical analysis are non-stationary, one or more linear combinations of these time-series are stationary. Johansen derived two tests, the λ-max (maximum eigenvalue test) and the λ-trace (or trace test) to check cointegration. Each test has slightly different criterion. The Max test is expressed as:
(5)
The maximum eigenvalue test tests the null of r cointegrating vectors against the alternative hypothesis of r + 1 cointegrating vectors.
The trace test is expressed as:
(6)
Here T is the sample size and is the ith largest canonical correlation.
Detection of linear, stationary combination of variables confirms the existence of a long-run relationship between them. Consequently, the cointegration tests can provide key information on the role of FDI in GDP growth rate for the countries under the study.
Lag length to be used is also important and usually three methods, namely, Akaike [22] , Schwarz [23] and Hannan-Quinn [24] are used for the determination of lag length. These are considered to be the classical procedures for determining lag length [25] . Two more criteria, namely, LR (sequential modified LR test statistic) and FPE (Final prediction error) are also used by researchers to determine the lag order.
4.5. Vector Error Correction Method (VECM)
When a set of variables are found to have one or more cointegrating equations, VECM is applied as it adjusts to both short run changes in the variables and deviations from the long-run equilibrium. VECMs are a reparameterization of VAR models in levels and they can be represented symbolically as:
(7)
Equation (7) is called a VECM because it includes the lagged error correction (EC) term represented by .
Here, Γ is the matrix of variables.
The matrix β is the cointegrating matrix and the matrix α is the loading matrix.
is the non-stationary variable.
If the coefficient of the cointegrating model is negative in sign and significant then it indicates a long-run causality running from one variable in the system to the other variable. Short run causality is indicated when coefficient of the lagged value of the variable under consideration is not equal to zero. The null of this variable being equal to zero is tested through Wald test and it is rejected on the basis of the low p value (less than 0.05) of chi-square statistic.
5. Analysis and Discussion of Results
The results of the empirical tests conducted on the data series under the study including ordinary least squares regression, unit root test, Granger causality test, Johansen co-integration test and vector error correction model are summarized in this section.
5.1. Ordinary Least Squares Regression
OLS regression has been performed to evaluate the dependency relationship between GDP growth rate and FDI for each of the country under the study. The results for all six countries under the study are summarized in Table 4 and analyzed.
1) Bhutan
The F-statistic is statistically significant, confirming the existence of linear relationship between GDPGR and FDI. The equation with coefficients is represented as:
GDPGR = 0.6351 + 19.39 × FDI (8)
Thus, one unit increase in FDI can be expected to cause 19.39 unit increase in GDP growth rate. However, the R-squared is 0.327, indicating that only 32.7 percent of GDPGR variation is explained by this linear model. Though, the higher the R-squared, the better the model fits the data, yet low R-squared cannot be used to infer absence of significant relationship between GDP and FDI. In general, R-squared does not indicate whether a regression model is adequate and there can be low R-squared value for a good model.
2) Ethiopia
The F-statistic is statistically significant, confirming the existence of linear relationship between GDPGR and FDI. The equation with coefficients is represented as:
Table 4. Results of OLS regression for GDP growth rate and FDI for selected countries.
Source: Based on authors’ calculations.
GDPGR = 11.82 + 17.96 × FDI (9)
Thus, one unit increase in FDI can be expected to cause 17.96 unit increase in GDP growth rate.
The R-squared value suggests that the model explains 73.8 percent of the variability of the GDPGR data around its mean.
3) India
The ordinary least square method indicates that there is a positive relationship between FDI and GDPGR. The equation with coefficients is represented as:
GDPGR = 337.66 + 39.00 × FDI (10)
Thus, one unit increase in FDI can be expected to cause 39 unit increase in GDP growth rate. The R-squared value suggests that the model explains 86.4 percent of the variability of the response data around its mean.
4) Brazil
The ordinary least square method indicates that there is a positive relationship between FDI and GDP.
GDP = 405.16 + 21.55 × FDI (11)
Thus, one unit increase in FDI can be expected to cause 21.55 unit increase in GDP growth rate. The R-squared value suggests that the model explains 88.3 percent of the variability of the response data around its mean.
5) United Kingdom
The F-statistic is statistically significant, confirming the existence of linear relationship between GDPGR and FDI. The equation with coefficients is represented as:
GDPGR = 1522.42 + 5.10 × FDI (12)
Thus, one unit increase in FDI can be expected to cause 5.1 unit increase in GDP growth rate. However, R-squared is 0.316, indicating only 31.6 percent of GDPGR variation is explained by this linear model.
6) United States of America
The Ordinary least square method indicates that there is positive relationship between FDI and GDPGR. The equation with coefficients is represented as:
GDPGR = 6266.23+26.43 × FDI (13)
Thus, one unit increase in FDI can be expected to cause 26.43 unit increase in GDP growth rate. The R-squared value suggests that the model explains 68.7 percent of the variability of the response data around its mean.
5.2. Unit Root Test
The results of unit root test are summarized in Table 5. All twelve data series under the study are found to be non-stationary at levels and stationary at first difference using the ADF test. Thus all series are integrated of I (1) order. This is important because to apply Johansen cointegration test, the data series should be nonstationary at levels and integrated of the same order.
Table 5. Results of unit root test for GDP growth rate and FDI for selected countries.
*significance at 5% level. Source: Based on authors’ calculations.
5.3. Granger Causality Test
Results of Granger causality test are presented in Table 6. It can be inferred that the GDP growth rate does not Granger cause FDI for any of the countries under the study. Further, unidirectional causality from FDI to GDPGR is also found only in the case of India and USA.
5.4. Johansen Cointegration Test
Lag length has been calculated for each of the country under the study using the five criteria mentioned above. The lag length for Bhutan is 4 on the basis of LR, FPE and AIC. For all other countries under the study it is 1, based on all five criteria. It can be seen in Table 7 that Bhutan, Brazil and USA have no cointegration, indicating the absence of long-run equilibrium relationship between GDPGR and FDI for each of these countries over the period of the study. On the other hand, India, Ethiopia and UK have been found to have cointegration between FDI and GDPGR over the period of the study.
To ensure robustness of the findings, further analysis has been carried out to explore the nature of causality among the variables under the study. Since Granger causality did not shed much light on the direction of causality between the two variables for each of the country under the study, vector error correction model (VECM) has been estimated for the countries which are found to have cointegration between the variables, that is, India, Ethiopia and UK.
5.5. Vector Error Correction Model (VECM)
Since a stable long-run relationship between FDI and GDPGR has been found for Ethiopia, India and UK, it is possible to estimate an error correction (EC)
Table 6. Results of Granger causality test for GDP growth rate and FDI for selected countries.
Source: Based on authors’ calculations.
Table 7. Results of Johansen co-integration test for GDP growth rate and FDI for selected countries.
*denotes rejection of the hypothesis at; **MacKinnon-Haug-Michelis (1999) p-values. Source: Based on authors’ calculations.
model to capture both, the short-and long-run behavior of the FDI and GDPGR relationship [26] . VECM is helpful to understand the speed of adjustment towards equilibrium and evaluate short- and long-run causality running from FDI to GDPGR.
Treating GDPGR as the “dependent” variable, EC models estimated for these three countries are reported in Table 8. The target models for the three countries are:
(14)
(15)
(16)
In the above equations, C(1) is the coefficient of the cointegrating model. It is the error correction term. As can be observed in Table 8, for all three countries, the coefficient of the cointegrating models is negative in sign and significant, indicating long run causality running from FDI to GDPGR. In the case of Ethiopia, the EC term suggests that a 10 percent deviation from the long-run GDPGR and FDI relationship during the current year is corrected by about 6.6 percent on an annual basis. In the case of India and UK, the annual correction is 10.3 percent and 5.7 percent respectively.
Wald test output, given in Table 8, indicates that there is no short-run causality running from FDI to GDPGR for all three countries. This is concluded on the
Table 8. VEC models estimated for Ethiopia, India and UK.
Source: Based on authors’ calculations.
basis of the p-value of the chi-square test statistic generated in the Wald test, being greater than 0.05.
All three models indicating long-run causality need to be subjected to diagnostic checking to evaluate the model fit. This has been done using the F statistic. Further, the strength of relationship has been explored using R-squared. Both values for all three countries are given in Table 8.
For Ethiopia, the R-squared is 0.354, which is quite low. F-statistic is statistically significant at 5percent level, indicating a good fit.
For India, the R-squared is 0.522, which is not so low. F-statistic is statistically significant at 5percent level, indicating a good fit.
For UK, the R-squared is 0.402, which is quite low. F-statistic is statistically significant at 5percent level, indicating a good fit.
Since all models are indicating a good fit, residual diagnostic has also been undertaken in terms of checking for serial correlation, heteroskedasticity and normality of distribution. Absence of correlation, existence of homoscedaticity and normal distribution of residuals are essential preconditions for any model to have meaningful predictive value. The results are presented in Table 9.
The results of the Breusch-Godfrey serial correlation LM Test reveal that the residuals of VEC model for Ethiopia have serial correlation as the p-value of the observed R-squared statistic is less than 0.05. That is not desirable. In case of India and UK, there is no serial correlation in the residual series, confirming a good fit of the VEC model.
Breusch-Pagan-Godfrey test for heteroskedasticity shows that the residuals are homoscedastic for the VEC model of India and Ethiopia, confirming good fit of these models. However, heteroskedasticity in the residual series is found in the case of VEC model of UK. This is not desirable.
Normality of residuals has been tested using the Jarque Bera test statistic. The residuals of the VEC models of all countries are found to be normally distributed.
Table 9. Diagnostic tests of residuals of the VECM estimated for Ethiopia, India and UK.
Source: Based on authors’ calculations.
In summary, the VEC model of Ethiopia has the problem of serial correlation of residuals and R-squared of only 40 percent. So the model cannot be accepted. In the case of India, the diagnostic tests confirm the goodness of fit on all parameters and R-squared of 52 percent is quite acceptable. The VEC model of UK is also rejected as the residuals suffer from the problem of heteroskedasticity.
6. Conclusions
The main objective of this study is to identify interactive relationship between FDI and GDP growth rate for different types of economies in the world. To achieve the objective of the study, the annual FDI and GDP growth rate data, spanning a period from 1987 through 2016, has been used for six countries, namely Bhutan, Ethiopia, India, Brazil, UK and USA.
To begin with, preliminary analysis is performed using OLS regression to understand the nature of relationship between the two variables under the study for each of the six countries. The empirical analysis on basis of OLS method suggests that there is a positive relationship between FDI, the independent variable, and GDP growth rate, the dependent variable, for all countries under the study. However, based on the value of R-squared, the relationship can be concluded to be weak for Bhutan and UK and moderate for US.
The results of unit root test suggest that the variables used in this study are nonstationary at levels but stationary at first difference, thereby, integrated of same order I (1).
Granger causality test results suggest that there is no causality between FDI and GDP growth rate for any of the country under the study except India and USA, where there is a unidirectional causality running from FDI to GDPGR.
Further, Johansen cointegration test indicates that there is no linear long-run equilibrium relationship between FDI and GDP growth rate in the case of Bhutan, Brazil and USA. Due to detection of long run cointegrating relationship between the two variables for Ethiopia, India and UK, VEC model is also estimated for them to capture the behaviour of short- and long-run causality running from FDI to GDPGR. The models reveal the absence of short-run causality for all three countries. Of the three VEC models constructed, only the model estimated for India is found to pass all diagnostic tests for goodness of fit.
The cointegrating relation between FDI and GDPGR for India has shown that the two can be expected to move in tandem in the long-run and an increase in FDI can be expected to increase GDPGR. Further, based on the analysis of the unrestricted VECM specifications, it can be concluded that a 10 percent deviation from the long-run GDPGR and FDI relationship during a given year, gets corrected in the subsequent year by 10.3 percent.
The study has some interesting implications. The most obvious outcome of the study is that in the case of India, the policy makers can focus on FDI as a means to boost GDP growth rate in the long-run. The same is not suggested for other five countries under the study. Furthermore, the results are not specific to any economy-type, indicating that no generalization can be made for FDI and GDPGR relationship on the basis of the state of development of the country under consideration. For instance, both India and Brazil are developing economies but causality and cointegration between the variables are there found only for India.
7. Limitations of the Study and Directions for Future Research
Though the study has reported some interesting findings, further research and data are needed to come to more universal and robust conclusions regarding the nature of causality relationship between FDI and GDPGR. One of the limitations of the study is the sample size used. A larger sample size would ensure that the results are not taken as tentative. The second limitation pertains to the availability of data. The lack of availability of data prevented the authors from analyzing more countries in three broad economy groups. Again, analysis across large number of countries would make findings more robust.
Further, at the methodological level, the use of VECM has certain limitations. The VECM framework models the error correction mechanism of variables to their long-run equilibrium without determining, apriori, the endogeneity or exogeneity of the variables used in the model. The direction of causality between the variables is determined on the basis of econometric tests rather than on economic theory. The approach itself is, thus, criticized at time for it’s a prioiri, atheoretic and empirical methodology. However, VECM is used frequently by researchers as it has been found to generate better forecasts than the complex models rooted in economic theory.
Future research can be undertaken to validate the findings of the study using data spanning across longer time period for the same set of countries. More countries of each type can also be used to evaluate if it is possible to concluded causal relation between the two variables in the context of the type of economy and its state of development. Further, VAR (vector autoregression) can be applied to the data series of the countries where no cointegration was detected.
Acknowledgements
The authors are thankful to Madhur Saxena and Aritra Guha, PGDM (2016-2018), K J Somaiya Institute of Management Studies & Research, Mumbai, for their help in data collection and preliminary analysis.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Talwar, S. and Srivastava, S. (2018) Integration of GDP and FDI in Economies at Different Stages of Growth. Theoretical Economics Letters, 8, 2199-2219. https://doi.org/10.4236/tel.2018.811144
References
- 1. Takaendesa, P. and Odhiambo, N.M. (2007) Financial Sector Development and Economic Growth: An Empirical Analysis of Two Southern African Countries. Studies in Economics and Econometrics, 31, 61-80.
- 2. Aziakpono, M.J. (2011) Financial Development and Economic Growth: Theory and a Survey of Evidence. Studies in Economics and Econometrics, 35, 15-43.
- 3. Le Roux, P. and Gorlach, V. (2011) An Econometric Analysis of the Impact of Economic Freedom on Economic Growth in the SADC. Studies in Economics and Econometrics, 35, 1-14.
- 4. De Beer B., Rangasamy, L. and Rangasamy, L. (2015) Some Impacts of South African FDI Flows on the Current Account Balance. Studies in Economics and Econometrics, 39, 99-116.
- 5. Dao, M.Q. (2014) Drivers of Economic Growth in Developing Countries. Studies in Economics and Econometrics, 38, 75-85.
- 6. Alemu, A.M. (2017) Analyzing the Effects of Foreign Aid vs. FDI on Economic Growth in Africa. Journal of Economic Development, Management, IT, Finance & Marketing, 9, 1-13.
- 7. Koroci, A. (2018) Does FDI Influence Economic Growth in Albania? Academic Journal of Business, Administration, Law & Social Sciences, 4, 144-151.
- 8. Agrawal, G. (2015) Foreign Direct Investment and Economic Growth in BRICS Economies: A Panel Data Analysis. Journal of Economics, Business and Management, 3, 421-424. https://doi.org/10.7763/JOEBM.2015.V3.221
- 9. Silajdzic, S. and Mehic, E. (2016) Absorptive Capabilities, FDI, and Economic Growth in Transition Economies. Emerging Markets Finance & Trade, 52, 904-922. https://doi.org/10.1080/1540496X.2015.1056000
- 10. Gunby, P., Jin, Y. and Robert Reed, W. (2017) Did FDI Really Cause Chinese Economic Growth? A Meta-Analysis. World Development, 90, 242-255. https://doi.org/10.1016/j.worlddev.2016.10.001
- 11. Liu, X., Luo, Y., Qiu, Z. and Zhang, R. (2014) FDI and Economic Development: Evidence from China’s Regional Growth. Emerging Markets Finance & Trade, 50, 87-106. https://doi.org/10.1080/1540496X.2014.1013852
- 12. Nwaogu, U. and Ryan, M. (2015) FDI, Foreign Aid, Remittance and Economic Growth in Developing Countries. Review of Development Economics, 19, 100-115. https://doi.org/10.1111/rode.12130
- 13. Tsitouras, A. (2016) What Can Trigger the Resumption of Economic Growth in a Small Open Economy Like Greece: Exports or Inward FDI? International Economic Journal, 30, 504-526. https://doi.org/10.1080/10168737.2016.1151068
- 14. Cucos, P.R. (2016) The Effects of Foreign Direct Investment on the Economies of Central and Eastern Europe Countries. Annals-Economy Series, 4, 200-207.
- 15. Oladipo, O.S. (2013) Does Foreign Direct Investment Cause Long Run Economic Growth? Evidence from the Latin American and the Caribbean countries. International Economics & Economic Policy, 10, 569-582. https://doi.org/10.1007/s10368-012-0225-4
- 16. Dickey, D.A. and Fuller, W.A. (1979) Distribution of the Estimators for Autoregressive Time Series with a Unit Root. Journal of the American Statistical Association, 74, 427-431.
- 17. Dickey, D.A. and Fuller, W.A. (1981) Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica, 49, 1057-1072. https://doi.org/10.2307/1912517
- 18. Granger, C.W.J. (1969) Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica, 37, 424-438. https://doi.org/10.2307/1912791
- 19. Granger, C.W.J. (1988) Some Recent Developments in a Concept of Causality. Journal of Econometrics, 39, 36-67. https://doi.org/10.1016/0304-4076(88)90045-0
- 20. Seabra, F. and Flach, L. (2005) Foreign Direct Investment and Profit Outflows: A Causality Analysis for the Brazilian Economy. Economics Bulletin, 6, 1-15.
- 21. Johansen, S. (1991) Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica, 59, 1551-1580. https://doi.org/10.2307/2938278
- 22. Akaike, H. (1974) A New Look at the Statistical Model Identification. IEEE Transactions on Automatic Control, 19, 716-723. https://doi.org/10.1109/TAC.1974.1100705
- 23. Schwarz, G. (1978) Estimating the Dimension of a Model. The Annals of Statistics, 6, 461-464. https://doi.org/10.1214/aos/1176344136
- 24. Hannan, E. and Quinn, B. (1979) The Determination of the Order of an Auto Regression. Journal of the Royal Statistical Society, Series B (Methodological), 41, 190-195.
- 25. Lutkepohl, H. (1993) Introduction to Multiple Time Series Analysis. Springer, New York. https://doi.org/10.1007/978-3-642-61695-2
- 26. Engle, R.F. and Granger, C.W.J. (1987) Cointegration and Error Correction: Representation, Estimation, and Testing. Econometrica, 55, 252-276. https://doi.org/10.2307/1913236