Received 23 July 2016; accepted 22 August 2016; published 25 August 2016

ABSTRACT

We develop an analysis of optimal formulas for subnational tax revenue sharing for two cases of interest: when local public goods (lpg’s) show spillovers and are inter-regional perfect and imperfect substitutes. Our analysis could be relevant to understand the determinants of feasible competing alternatives for the design of tax revenue sharing systems. Our study shows that: 1) Inter-regional spillovers should be taken into account in the design of formulas for subnational revenue sharing when lpg’s are perfect inter-regional substitutes but should not be taken into account to supply lpg’s that are imperfect substitutes; 2) The distribution of preferences for lpg’s and population should be considered in formulas for revenue sharing when subnational governments provide both lpg’s that are perfect and imperfect substitutes; 3) For local public goods that are imperfect substitutes, the share of tax revenue is first increasing and then decreasing with increases in the population of the district; 4) For perfect substitute-lpg’s, the share of tax revenue in the district is increasing and concave with the district’s population; 5) The distribution of income should not be considered in the design of formulas for lpg’s that are perfect and imperfect substitutes. Other empirically relevant comparative analyses are considered in the paper.

Keywords:

Local Public Goods, State and Local Budget and Expenditures, Intergovernmental Transfers, Inter-Regional Externalities, Federalism

1. Introduction

Tax revenue sharing seeks to distribute revenue for central and subnational governments from a given tax base. Some of the advantages of tax revenue sharing recognized in the literature include: 1) Tax harmonization between the central and subnational governments to reduce inefficiency costs from tax competition; 2) Rao [1] argues that tax revenue sharing leads to welfare gains by ensuring greater subnational fiscal autonomy (by ensuring subnational governments a source of revenue), and 3) Revenue sharing is a tool to deal with vertical fiscal imbalances.

Tax revenue sharing is commonly implemented in many developed and developing countries through the use of formulas for the allocation of tax revenue between the central and subnational governments. Rao [1] classifies revenue-sharing systems in two types: in the first type, the central and sub-national governments share a tax base and different levels of governments can determine tax rates. In the second type, one level of government could collect tax revenue that is shared among different levels of governments¹. In spite of the empirical relevance of this policy, there is little formal research on the optimal design of formulas for subnational revenue sharing². Such analysis is worthwhile because knowing the properties of different forms of subnational revenue sharing systems would help us to identify potential advantages and shortcomings of feasible policy options. In this paper we seek to contribute to fill this gap in the literature and we analyze the optimal design of subnational tax revenue sharing. To do so, we study a model with a benevolent social planner in which subnational governments provide local public goods with inter-regional spillovers. The central government selects the nationwide tax rate on income to determine the optimal size of tax revenue and its shares to be allocated to subnational governments.

The main distinction of our analysis with respect the literature is that we consider the optimal design of formulas for subnational revenue sharing when local governments provide public goods with spillovers in two cases of interest: when local public goods are perfect and imperfect inter-regional substitutes^3,4. The main findings of our paper are the following: 1) Inter-regional spillovers should be taken into account in the design of formulas for revenue sharing when lpg’s are perfect inter-regional substitutes but should not be taken into account for imperfect substitutes; 2) The inter-regional distribution of preferences for lpg’s and population should be considered in formulas for revenue sharing when subnational governments provide lpg’s that are both perfect and imperfect substitutes; 3) For local public goods that are imperfect substitutes, an increase in the population of the district leads to an ambiguous outcome in the share of tax revenue in the district: for sufficiently high (low) initial values of the share of tax revenue, an increase in the district’s population leads to a fall (increase) in the share of tax revenue allocated to the district; 4) For perfect substitute-lpg’s, the share of tax revenue in the district is increasing and concave with the district’s population; 5) The distribution of income should not be considered in the design of formulas for lpg’s that are perfect and imperfect substitutes. Finally, we develop other comparative analysis on the optimal shares to be allocated among subnational governments.

The structure of the paper is as follows: in Section 2, we develop optimal formulas for tax revenue sharing for an economy with local public goods that are imperfect inter-regional substitutes. Section 3 contains the analysis for an economy with perfect substitutes. Section 4 concludes.

2. Optimal Tax Revenue Sharing for Local Public Goods that Are Imperfect Inter-Regional Substitutes

Consider an economy with individuals living in districts 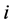and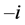. In our economy, the central government is responsible for collecting tax revenue and allocating (through the use of formulas) the shares of tax revenue for all districts. For simplicity of the analysis, we assume that local governments use the resources allocated to them by the central government to provide local public goods. 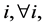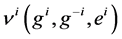In district there is a representative individual with an endowment and his indirect preferences are given by where 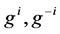are local public goods supplied by districts 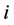and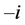. Direct preferences are given by 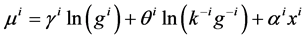where 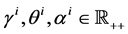are positive constants related with the individual’s intensity of preferences over local public goods and the private good ⁵. The parameter measures the extent of spillovers, if 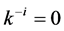there is no spillovers and if were equal to one then the local public good would be a pure national public good. The budget constraint of the individual is given by where is a proportional income tax implemented by the central government. In this economy, there is inter-regional heterogeneity of preferences, that is and without loss of generality we assume.

. To see that our preference relation for and characterizes local public goods that are imperfect inter-re- gional substitutes, note that the elasticity of substitution between and is positive but finite since where . In the case of perfect inter-regio-

nal substitutes, the elasticity of substitution is infinite (see Section 3).

We consider a benevolent social planner ruling the central government that seeks to maximize the nation’s so- cial welfare where are the populations of districts and. The problem of policy design for the central government is to maximize by choosing the size of the pro- portional income tax the budget B, and the formula for sharing revenue in districts and, to finance local public goods. The budget constraint of the central government is where is the central government’s budget. The distribution of tax revenue in the economy is determined by formulas for revenue sharing such that the budget constraints of subnational governments are given by and where is the share of the budget allocated to finance the local public good of district. For simplicity of the analysis, districts and only supply, respectively, and. In this section, we analyze the case of local public goods that are imperfect substitutes, which are defined by a finite elasticity of substitution, while for the case of local public goods that are perfect substitutes (analyzed in Section 3) the elasticity of substitution is infinite⁶. Formally, the problem of tax revenue sharing for the central government when local public goods are imperfect substitutes is:

(1)

(2)

where is the indirect utility function of the representative individual of district on feasible local public goods (a similar expression is given for).

Proposition 1. The optimal budget and formulas for distribution of tax revenue for local public goods that are imperfect inter-regional substitutes of districts and are given by:

(3)

With and

(4)

(5)

Proof

The first order conditions for the government’s problem are:

(6)

(7)

Rearrange terms to obtain conditions (3), (4) and (5).

Proposition 2. The optimal budget and formulas for distribution of tax revenue satisfy the following properties:

2.1) The implied distribution of local public goods, is Pareto efficient.

2.2) is a constant:.

2.3) The share of tax revenue allocated in district, also satisfies the following:

a) as and

b)

c)

d), that is is non decreasing with, and

e), that is is non decreasing with, and

Proof

See the Appendix.

Proposition 2 says that the equilibrium distribution of is Pareto efficient since takes into account the nationwide distribution of social marginal costs and benefits of local public goods. For this reason we can’t find an alternative feasible allocation in which we can benefit at least one individual without hurting someone else in this economy. Some other interesting results of our analysis are the following: for a local government in district supplying an imperfect substitute-local public good, the optimal formula for tax sharing, , is constant (see proposition 2.2) and it depends only on the distribution of parameters related with the intensity of preferences of individuals for local public goods in districts and, that is, and the distribution of the population in the economy (see condition 4).

An issue of interest for the design of a policy of tax revenue sharing is the relationship of with the dis-

trict’s population. Our analysis suggests that as. This is relevant for policy design

since empirical evidence suggests the use of linear formulas between and (see [10] ). However, our analysis suggests that the effect of an increase in the population of district over the share of tax revenue to be

allocated to district is contingent to the level of. For sufficiently low values of (for)

an increase in should lead to an increase in. However, for sufficiently high levels of (for

) an increase in should lead to a fall in. The explanation of this result is straightforward: from the optimality condition where

is the net social marginal benefit for residents of district of increasing where

is the gross social marginal benefit for residents of district of increasing (an increase in leads to a higher level of the local public good supplied by district which increases the wellbeing of residents of that district). Moreover, a higher means that falls which leads to a lower supply of and the ben-

efits for residents of district from consuming fall by. Hence the net benefit of a marginal in- crease in is. If then hence an increase in

leads to a net increase in the social marginal benefits of residents of district which leads to a higher share of

tax revenue allocated to this district (the opposite occurs if).

Other interesting outcomes from the characterization of are: the formula for does not depend on the distribution of spillovers and (see proposition 2.3b). The explanation of this outcome is that the marginal social benefits and costs of a change in do not depend on and (see condition 7). A similar explanation is given to the outcome that the distribution of income should not be considered in the design of formulas for lpg’s that are imperfect substitutes since (see condition 2.3c). Finally, proposition 3 says that an increase in the intensity of preferences of residents in district and of residents of district for the local public good provided by district (that is increases, respectively, in and) should increase the share of tax revenue allocated to district. This is the case because higher values of and increase the nation wide’s social marginal benefits of the public good provided by district.

3. Optimal Tax Revenue Sharing for Local Public Goods that Are Perfect Inter-Regional Substitutes

In this section, we analyze the case for formulas for subnational tax revenue sharing when local public goods are perfect inter-regional substitutes which means that the elasticity of substitution between and is infinite. To distinguish our notation from our previous section, we denote as the equilibrium level of the budget and as the allocation formula of tax revenue for district. For this case,

is the indirect utility for a resident in dis-

trict where are positive constants and and ⁷. For this economy, the problem of policy design is⁸:

(8)

(9)

Proposition 3. The optimal budget and formulas for distribution of tax revenue for local public goods that are perfect inter-regional substitutes in districts and are given by:

(10)

Recall and

(11)

And

(12)

Proof

The first order conditions for the government’s problem are:

(13)

(14)

Rearrange terms to obtain conditions (10), (11) and (12).

Proposition 4. The optimal budget and formulas for distribution of subnational tax revenue satisfy the following properties:

4.1) The implied distribution of local public goods, is Pareto efficient.

4.2) is a constant:

4.3) The share of tax revenue allocated in district, satisfies:

a) and

b) and.

c) and

d)

e) if with

f) if with

Proof

See the Appendix.

Proposition 4 shows some comparative static results on the determinants of formulas for revenue sharing for local public goods that are perfect inter-regional substitutes. In particular, is non decreasing with the population of the district, however, this relationship is not linear since. In addition, the distribution of tax revenue for district is increasing on the spillovers of the public good provided by district, and decreasing in the spillovers of the local public good supplied by district, (see propositions 4.3.b and 4.3c). These last results are very intuitive: a higher level of increases the nationwide social marginal benefits of (by the effect of the spillovers of over district) which leads to an increase in the tax revenue allocated to district. A similar effect occurs with an increase in which makes more attractive to allocate more resources in district and reduces. The distribution of income should not be considered in the design of formulas for lpg’s that are perfect substitutes since (see condition 4.3c). As in the previous section, the marginal social benefits and costs of a change in do not depend on and (see condition 11). Proposition 4 also shows that has an ambiguous relationship with the distribution of

the intensity of preferences for local public goods. To be specific, if and if then.

In terms of the practical significance of this paper, propositions two and four highlights the relevance of taking into account the inter-regional heterogeneity of preferences and the distribution of the country’s population in the allocation of tax revenue among sub-national governments, since the heterogeneity of preferences and population are the main determinants of formulas for local governments supplying local public goods that are perfect and imperfect inter-regional substitutes. In particular, one common determinant of formulas for revenue sharing is the district’s population. Our analysis shows that the relationship between the funds allocated in the district and the district’s population is not necessarily linear (a common practice in some countries, see [1] , [10] ) and in fact it could also be negative (an increase in the district’s population could lead to a lower share of the resources devoted to that district, see proposition 2.3a). Finally, the least intuitive finding of the paper is that the distribution of income in the federation should not determine the distribution of tax revenue sharing among sub-national governments. As mentioned before, in our paper this finding is explained by the fact that both the marginal social benefits and costs of allocating funds to some district in the federation do not depend on the household’s income. Although this result should be subject of further analysis to test whether this finding is general or closely related to the parametric functions used in this paper.

4. Concluding Remarks

In this paper, we study the optimal design of formulas for subnational revenue sharing when local governments provide public goods with spillovers in two cases of interest: when local public goods are perfect and imperfect inter-regional substitutes. Even though, tax revenue sharing policy is implemented in many developed and developing countries there is little formal research on the design of formulas for subnational revenue sharing. In this paper we seek to contribute to fill this gap. Our main contribution is to distinguish the determinants for optimal formulas for subnational revenue sharing when local governments provide local public goods with spillovers that are perfect and imperfect inter-regional substitutes. This analysis has the potential to provide relevant information for policy makers on the determinants and some properties of formulas for subnational tax revenue sharing.

Our analysis suggests the following: 1) Spillovers should be taken into account in the design of formulas for revenue sharing when lpg’s are perfect inter-regional substitutes but should not be taken into account for imperfect inter-regional substitutes; 2) The distribution of preferences for lpg’s and population should be considered in formulas for revenue sharing when subnational governments provide both lpg’s that are perfect and imperfect substitutes; 3) For local public goods that are imperfect substitutes, an increase in the population of the district leads to an ambiguous outcome in the share of tax revenue in the district: for sufficiently high (low) initial values of the share of tax revenue, an increase in the district’s population leads to a fall (increase) in the share of tax revenue allocated to the district; 4) For perfect substitute-lpg’s, the share of tax revenue in the district is increasing and concave with the district’s population; 5) The distribution of income should not be considered in the design of formulas for lpg’s that are perfect and imperfect substitutes. Other empirically relevant comparative analysis are considered in the paper.

Although the paper provides insights for the design of revenue sharing systems, it does not consider political institutions (such as electoral competition, the interaction between the executive and legislative bodies), the role of special interest groups and other issues raised by political economy models that might be central in shaping incentives of policy makers. Analysis on revenue sharing systems should also incorporate the role of mobility of households and firms, and adopt a systemic view of the optimal composition of the tax structure and spending of subnational governments and the central government. Future research on this topic should address these issues.

Acknowledgements

Raul Alberto Ponce Rodriguez thanks Consejo Nacional de Ciencia y Tecnología (CONACyT) for the financial support of the program “estancias sabáticas en el extranjero 2015” that helped to develop this research.

Cite this paper

Raul Alberto Ponce Rodriguez,Ikuho Kochi, (2016) Optimal Formulas for Subnational Tax Revenue Sharing. Theoretical Economics Letters,06,808-818. doi: 10.4236/tel.2016.64085

References

Appendix

Proposition 2. The optimal budget and formulas for distribution of tax revenue satisfy the following properties:

2.1) The implied distribution of local public goods, is Pareto efficient.

2.2) is a constant:.

2.3) The share of tax revenue allocated in district, also satisfies the following:

a) as and

b)

c)

d), that is is non decreasing with, and

e), that is is non decreasing with, and

Proof

2.1) Efficiency: local public goods are Pareto efficient. Since,

.

2.2) is a constant:. This follows trivially by the fact are constants. Mo-

reover, and

2.3) satisfies the following:

a) as and

From condition (4),. Since

, the term

. Moreover from

, it is simple to see that.

b)

From condition (4),.

c).

From condition (4),.

d) is non decreasing on and.

From (4), and

since

.

e) is non decreasing on and.

From (4), and

since

.

Proposition 4. The optimal budget and formulas for distribution of subnational tax revenue satisfy the following properties:

4.1) The implied distribution of local public goods, is Pareto efficient.

4.2) is a constant:

4.3) The share of tax revenue allocated in district, satisfies:

a) and.

b) and.

c) and.

d).

e) if with.

f) if with.

Proof

4.1) Efficiency: local public goods and are Pareto efficient since

and feasible

.

4.2) is a constant:. Since are constants. Moreover,

and

4.3) The share of tax revenue for district, , also satisfies the following:

a) and.

From (11),

since

.

It also holds that.

b) and

Note that and

.

c) and.

Define From proposition 4.3b

and.

d).

From condition (11),

e) if with

It is satisfied that

.

Moreover, it is simple to show.

f) if with.

From (11), as and.

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

NOTES

^*Corresponding author.

¹It is common that, under this type of revenue sharing, the central government is responsible for collecting tax revenue but subnational governments are in charge of the spending choices and (or) the administration of public programs.

²There is a large literature on the optimal design and effects of intergovernmental transfers, see (among many others) [2] - [5] , and more recently [6] . There has been also interest on revenue assignments, see [7] . However, to the best of our knowledge, there has been little interest on developing a formal theory of the optimal design of formulas for subnational revenue sharing.

³Spillovers of local public goods lead to some degree of inter-regional substitutability among lpg’s produced in different regions. Moreover, in real life, the mobility of households and firms makes lpg’s more substitutable. Hence, it is relevant to conduct an analysis of the distinction between lpg’s that are perfect inter-regional substitutes (which is the limiting case) and imperfect substitutes in the design of formulas for subnational tax revenue sharing. However, for simplicity of the analysis, in this paper we ignore inter-regional mobility. We leave such analysis for future research.

⁴In Section 2, we provide a formal distinction between local public goods that are perfect and imperfect inter-regional substitutes. A real life example of a perfect substitute-local public good with inter-regional spillovers could be productive local infrastructure (such as local bridges, roads etc.). To see this, consider a firm (similar examples can be found for the case of households) that sells products in all districts (regions). If a bridge in some district has a constant marginal rate of technical substitution with respect a bridge provided in some other district then these local public goods show spillovers and are considered as perfect inter-regional substitutes. For the case of imperfect substitutes, the marginal rate of technical substitution is not constant.

⁵Our choice of the utility function is for simplicity of the analysis. Moreover, this type of utility function is common in the literature see [8] and [9] , among many others.

⁶To distinguish local public goods that are perfect vs imperfect inter-regional substitutes, we use the elasticity of substitution

⁷To see that lpg’s are perfect inter-regional substitutes, note that the direct preferences of the representative individual of district are

where. Use the household’s budget constraint and the government’s budget con-

straint to characterize the indirect preferences denoted by. Recall, and since

and

⁸The indirect preferences of the representative individual of district are given by