Theoretical Economics Letters
Vol.06 No.02(2016), Article ID:65984,7 pages
10.4236/tel.2016.62032
From Disorder to Order
Xiaoguang Yue1, Yong Cao2, Michael McAleer3,4,5,6*
1Department of Engineering Management, School of Civil Engineering, Wuhan University, Wuhan, China
2Department of Computer Science, School of Computer and Information, Southwest Forestry University, Kunming, China
3Department of Quantitative Finance, National Tsing Hua University, Chinese Taipei
4Econometric Institute, Erasmus School of Economics, Erasmus University Rotterdam, Rotterdam, The Netherlands
5Tinbergen Institute, Amsterdam and Rotterdam, The Netherlands
6Department of Quantitative Economics, Complutense University of Madrid, Madrid, Spain

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 February 2016; accepted 24 April 2016; published 27 April 2016
ABSTRACT
In the physical and social sciences, and especially in physics and economics, respectively, order and disorder (alternatively, equilibrium and disequilibrium in economics) refer to the presence or absence of some symmetry or correlation in a many-particle system. It follows that it is important to examine whether there is any regularity hidden in the phase transition of the disorder- order relationship. In this paper a series of experiments are devised and executed to reveal the power law relationship between order and disorder, and to determine that the power law is indeed an important regular pattern in the phase transition from disorder to order.
Keywords:
Order, Disorder, Equilibrium, Disequilibrium, Power Law, Scale Invariance, Symmetry, Regularity, Physical Sciences, Social Sciences

1. Introduction
In the physical and social sciences, and especially in physics and economics, respectively, order and disorder (alternatively, equilibrium and disequilibrium in economics) refer to the presence or absence of some symmetry or correlation in a many-particle system.
Order is a necessary condition for any issue that the human mind might wish to understand. Arrangements such as the layout of a city or building, a set of tools, a display of merchandise, the verbal exposition of facts or ideas, or a painting or piece of music, are called orderly when an observer or listener can grasp their overall structure and the ramification of the structure in some detail.
In the presence of order (or equilibrium), it is possible to focus on what is alike and what is different, what belongs together, and what should be separated. When nothing superfluous is included and nothing indispensable is omitted, one can understand the interrelation of the whole and its parts, as well as the hierarchical scale of importance and power by which some structural features are dominant, and others are subordinate. The perceivable order tends to be manifested and understood as a reflection of an underlying order, whether physical, social, or cognitive.
Disorder (or disequilibrium) means a physical condition in which there is a disturbance of normal functioning, a condition in which things are not in their expected places, or a disturbance of the peace or of public order. In this connection, the term disorder is intended to mean that the single elements, with which the statistical approach operates, behave independently from one another. For example, thermal movement and white noise are manifestations of disorder.
Scientists have researched order and disorder for millennia. Entropy might be defined as the quantitative measure of the degree of disorder in a system. In information theory, entropy is also a measure of unpredictability of information content. There exist interesting problems of what a regular pattern relationship might be between disorder and order, and what mechanism might be determined as underlying the transition from disorder to order.
Physical, biological and economics systems are typically heterogeneous as individuals vary in their characteristics, their response to the external environment, and to each other. Ariel, Rimer and Ben-Jacob [1] examined the effect of heterogeneity in the context of the well-known scalar noise model. This model shows numerically that the system undergoes a phase transition between an ordered phase at low temperature/high density, and a disordered phase at high temperature/low density.
Woloszyn, Stauffer and Kulakowski [2] investigated the network model of community by Watts, Dodds and Newman as a hierarchy of groups [3] . Woloszyn et al. [2] used Glauber dynamics to investigate the order- disorder transition, and found the transition temperature. The results provided a mathematical illustration of the social ability to a collective action via weak ties, as discussed in Granovetter in 1973.
Lorinczi, Georgii and Lukkarinen [4] investigated the continuum q-Potts model at its transition point from the disordered to the ordered regime. They argued that the occurrence of a phase transition can be seen as a percolation in the related random cluster representation, and argued that the occurrence of a phase transition can be seen as percolation in the related random cluster representation.
Symbolic sequences have been analysed for an extended period in many areas, including economics, physics, biology, information science, and linguistics. There is an old saying in many cultures that says if billions of monkeys were to have tapped keyboards for billions of years, they are very likely to have written a Shakespearean masterpiece, or maybe even the Bible. This implies that there are some discernible patterns in the phase from disorder to order.
This paper designs an experiment-based method about symbolic sequences to research the regularity between order and disorder. About 128 students are asked to play monkeys to continue to tap keyboards thousands of times, and a power law is found in these experiments. It seems that a power law is indeed an emerging pattern from disorder to order.
The outline of the paper is as follows. Section 2 describes the power law, which is used widely in the physical and social sciences. Section 3 describes a series of experiments to reveal the regular patterns in the phase from disorder to order, and obtains the experimental results. Section 4 draws a conclusion that the power law is an important regular pattern that can be determined in the transition from disorder to order.
2. Power Law
Some classical distributions, such as the normal distribution, can be characterized by the mean and variance, but not all distributions are as straightforward to characterize. Among others, the power law has attracted particular attention over the years for its mathematical properties, which sometimes lead to surprising physical consequences, and for its appearance in a diverse range of natural and artificial phenomena.
The populations of cities, the intensities of earthquakes, volcanic activity and tsunami, the sizes of power outages, and financial turmoil, among others, are all viewed as having power law distributions. Quantities such as these are not well characterized by their typical or average values (see Clauset et al. [5] ). The power law describes the objects as self-similar under some change in scale, either strictly, or statistically.
Mathematically, a quantity x obeys a power law if it is drawn from a probability distribution:
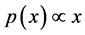 , (1)
, (1)
that is, a power law is a relationship between two scalar variables, x and y = p(x), which can be written as follows:
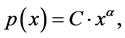 (2)
(2)
where C is the constant of proportionality and α is the exponent of the power law. Such a power law relationship shows as a straight line on a logarithmic graph as a logarithmic transformation of both sides of Equation (2) is equivalent to:
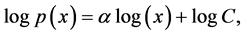 (3)
(3)
which has the same form as the equation for a straight line:
 (4)
(4)
The equation 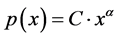 has a property that relative scale change p(sx)/p(x) = sα is independent of x. In this sense, p(x) lacks a characteristic scale. The constant α is an unknown exponent or scaling parameter of the distribution, and is scale invariant. As α and C are unknown constants, in practice they would be estimated from available data using standard estimation methods such as least squares.
has a property that relative scale change p(sx)/p(x) = sα is independent of x. In this sense, p(x) lacks a characteristic scale. The constant α is an unknown exponent or scaling parameter of the distribution, and is scale invariant. As α and C are unknown constants, in practice they would be estimated from available data using standard estimation methods such as least squares.
Specifications such as (2)-(4) are used widely in economics, for example, whereby output from a simple Cobb-Douglas production function depends exponentially (or log-linearly) on various inputs, such as labour, capital, energy and materials.
3. A Regular Pattern between Order and Disorder
Consider allowing students to play the above mentioned monkeys and ask them to continue to tap keyboards arbitrarily. The input random character sequence represents the disorder state, and the words that appear in the input sequence imply the order state.
Any regularity between order and disorder can be analysed, with the experiments devised as follows:
・ First, 128 students are asked to randomly tap the keyboard to input letters, and each student inputs 6000 letters arbitrarily.
・ Next the words in an electronic Oxford dictionary (more than 30,000) are input to a text file, and they are split by tab key in order that regular expression methods can be applied easily.
・ Then the number of words (according to the above text file of the Oxford dictionary), which appear in the input random character sequences of 2, 4, 8, 16, ∙∙∙, 128 students will be counted.
・ Finally, it can be determined whether a regular pattern such as a power law is found.
Of course, the power law requires varied scales. Here 2, 4, 8, ∙∙∙, 128 represent the nth power of 2 (n = 1, 2, 3, ∙∙∙, 7), and they are varied scales in the power law. The little corner of one input random character sequence is shown in following Figure 1. The text file of the electronic Oxford dictionary is shown in Figure 2. The number of words (according to the above text file of Oxford dictionary) appearing in input random character sequences of students is shown in Figure 3.
Then the number of words appearing in input random character sequences of 2, 4, ∙∙∙, 64, 128 students, respectively, are counted. Next the logarithm of the number of the input random sequences, the logarithm of the number of words appearing in random sequences (if the word appears repeatedly, it will be counted only once), and the logarithm of the cumulative number of words appearing in random sequences (if the word appears repeatedly, the cumulative number will be counted) are computed. The results are shown in Table 1.
We select 2 as a scale and take account of N(ϵ), which is the number of words appearing in the input random sequences. Then we change the scale with the nth power of 2 (n = 2, 3, ∙∙∙, 7) to obtain a new N(ϵ), and repeat the above steps to obtain a series of [ϵ, N(ϵ)] pairs. Then we treat the [ϵ, N(ϵ)] pair of series as a point in the logarithmic coordinate, and draw a log ϵ-log N(ϵ) chart to analyze the data.
It can be seen that the logarithmic points are almost in a straight line in Figure 4. The relationships between the number, cumulative number of words appearing and the number of input random sequences follow a power law. However, the logarithmic relationship between the cumulative number of words appearing and the number
Table 1. Logarithm of input random sequence number, number of words appearing and cumulative number of words appearing.
Figure 1. Part of one input random character sequence and the total of sequences is 128.
Figure 2. Text file of Oxford dictionary which includes words that occur more than 30,000 times.
Figure 3. Number of words that appear in the input random character sequences.
of input sequences fits the power law more accurately.
Next we count the number and the cumulative number of 2-, 3-, 4- and 5-letter words appearing in input random sequences, and obtain the new logarithmic relationships, which are shown in Figures 5-8.
It can be seen that the relationships between the number of the input random sequences and the number of 2-, 3-, 4- and 5-letter words appearing (if the word occurs repeatedly, we count it only once) do not follow the power law well.
However, the relationships between the number of the input random sequences and the cumulative number of 2-, 3-, 4- and 5-letter words appearing (if the word occurs repeatedly, we count the number of occurrences) follow the power law very well. It follows that the power law is an important regular pattern between order and disorder. The respective power law exponent α and coefficient C of 2-, 3-, 4- and 5-letterwords are shown in Table 2.
Figure 4. Logarithmic number of input random sequences.
Figure 5. Logarithmic relationships between the number and the accumulative number of 2-letter appearing words and the number of input random sequences.
Figure 6. Logarithmic relationships between the number and the cumulative number of 3-letter words and the number of input random sequences.
Figure 7. Logarithmic relationships between the number and the cumulative number of 4-letter words and the number of input random sequences.
Figure 8. Logarithmic relationships between the number and the cumulative number of 5-letter words and the number of input random sequences.
Table 2. The respective power law exponent and coefficient C of 2-, 3-, 4- and 5-letter words, namely the slope and the intercept of a log-log relationship in Figures 5-8.
4. Conclusions
The study of power laws spans many scientific disciplines, including economics, physics, biology, engineering, computer science, earth sciences, political science, sociology, and statistics.
In this paper, we devised and executed a series of experiments to reveal power law regularities between order and disorder, and obtained some experimental results. We counted the number of the input random character sequences and the accumulative number of words appearing in the input random sequences, and found that they follow the power law rather well.
The experimental results showed that the power law is indeed an important regular pattern in the phase transition procedure from disorder to order, or from disequilibrium to equilibrium in economics. Although there are many applications in the physical and social sciences, especially physics and economics, respectively, the mechanism underlying the power law requires further research in the future.
Acknowledgements
The first two authors acknowledge the financial support of the National Natural Science Foundation of China (NSFC) (61363061), and the third author wishes to thank the Australian Research Council and National Science Council (NSC), Taiwan.
Cite this paper
Xiaoguang Yue,Yong Cao,Michael McAleer,1 1,1 1,1 1, (2016) From Disorder to Order. Theoretical Economics Letters,06,282-288. doi: 10.4236/tel.2016.62032
References
- 1. Ariel, G., Rimer, O. and Ben-Jacob, E. (2015) Order-Disorder Phase Transition in Heterogeneous Populations of Self-Propelled Particles. J Stat Phys, 158, 579-588.
http://dx.doi.org/10.1007/s10955-014-1095-7 - 2. Woloszyn, M., Stauffer, D. and Kulakowski, K. (2007) Order-Disorder Phase Transition in a Cliquey Social Network. European Physical Journal B, 57, 331-335.
http://dx.doi.org/10.1140/epjb/e2007-00169-4 - 3. Watts, D.J., Dodds, P.S. and Newman, M.E.J. (2002) Identity and Search in Social Networks. Science, 296, 1302-1305.
http://dx.doi.org/10.1126/science.1070120 - 4. Lorinczi, J., Georgii, H.O. and Lukkarinen, J.M. (2005) The Continuum Potts Model at the Disorder Corder Transitional Study by Cluster Dynamics. Journal of Statistical Mechanics Theory and Experiment, 128, 62-69.
- 5. Clauset, A., et al. (2009) Power-Law Distributions in Empirical Data. Siam Review, 51, 661-703.
http://dx.doi.org/10.1137/070710111
NOTES
*Corresponding author.











