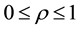Theoretical Economics Letters
Vol.05 No.02(2015), Article ID:55862,12 pages
10.4236/tel.2015.52037
The Inter-Temporal Causal Nexus between Indian Commodity Futures and Spot Prices: A Wavelet Analysis
Anto Joseph1*, Garima Sisodia1, Aviral Kumar Tiwari2
1Department of Finance and Accounting, IBS, Hyderabad, India
2Department of Economics, IBS, Hyderabad, India
Email: *ajoseph@ibsindia.org, garimasisodia@ibsindia.org
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 March 2015; accepted 20 April 2015; published 22 April 2015
ABSTRACT
This study examines the inter-temporal causal nexus between Indian commodity futures and spot prices by using wavelet analysis. Wavelet analysis offers an effective alternative tool to examine the inter-temporal causal relationship in time as well as frequency domains, providing a deeper understanding of direction, strength and extent of such causal relationship; whereas traditional econometric causality analysis tools focus only on the time domain. The empirical results of wavelet analysis suggest that the Indian commodity futures market has a powerful price discovery function in all the selected commodities, which in turn indicates the efficiency of the Indian commodity futures market.
Keywords:
Commodity Futures, Price Discovery, Causality, Wavelet Analysis

1. Introduction
Among several functions performed by commodity futures market, arguably price discovery is considered as the most important function. The quintessence of price discovery is to create a competitive reference price from which the spot price can be derived. Thus, futures price serves as the market’s expectation of subsequent spot price. Studies in market microstructure indicate that information is captured first in the futures market due to some of its inbuilt structural advantages and therefore results in price being discovered in the futures market. This subsequently gets transmitted to spot prices either instantaneously or with some lag. If futures market leads spot market, indicates futures market performs price discovery function and it is usually considered as one of the most important parameters for evaluating the efficiency of futures market. The extent to which futures market performs price discovery function can be measured from the inter-temporal causal relationship between futures and spot prices.
There is a significant amount of literature provides insights into the inter-temporal causal relationship between commodity spot and futures prices. For example, Garbade and Silber [1] examined the price discovery role of futures prices and the effect of arbitrage on price changes by developing a partial equilibrium model which characterises the price movements in cash and futures markets for storable commodities. Following Garbade-Silber model, Oellermann, Brorsen and Farris [2] and Schroeder and Goodwin [3] examined the feeder cattle market and the live hog market, respectively. Koontz, Garcia and Hudson [4] investigated the spatial price discovery mechanism in the livestock market by using Geweke’s causality test [5] and they found high degree of interaction between spot and futures prices. Iyer and Pillai [6] extended the model of Garbade and Silber [1] , by superimposing a two-regime TVAR model and examined whether futures markets play a dominant role in the price discovery process for six commodities.
Subsequent to the introduction of the statistical concept of cointegration of time series by the seminal works of Granger [7] , Engle and Granger [8] and Johansen [9] , several researchers have applied cointegration and error correction models to examine the long-run and short-run equilibrium relationship between futures and spot prices. For example, Serletis and Banack [10] , Crowder and Hamed [11] and Schwarz and Szakmary [12] examined efficiency of petroleum futures markets by using cointegration analysis. Chowdhury [13] examined the nonferrous metal futures markets’ efficiency by using cointegration for copper, lead, tin and zinc. Beck [14] performed tests on long run and short run market efficiency for cattle, orange juice, hogs, corn, copper, cocoa and soybean, with the help of cointegration and error correction model. McKenzie and Holt [15] investigated the long run and short run market efficiency using cointegration and GQARCH-M-ECM. The results show that live cattle, hogs, corn and soybean meal futures markets are both efficient and unbiased in the long run, however, inefficiencies and pricing biases in the form of a dynamic lag structure exist in the short run.
The existence of nonlinear structure in the process generating spot and futures returns and testing for nonlinear causal relationships have received considerable attention after the seminal work of Savit [16] [17] . He proposes that financial and commodity markets are likely to be examples of dynamical systems manifesting nonlinearities. These nonlinearities are normally attributed to nonlinear transaction cost functions, the role of noise traders, and to market microstructure effects (Abhyankar [18] ). As a result, many studies started focusing on the nonlinear causal relationships between futures and spot prices. For example, Silvapulle and Moosa [19] examined the relationship between the spot and futures prices of WTI crude oil by using linear and nonlinear Granger-causality tests. Linear causality test result showed that futures prices lead spot prices, but nonlinear causality test established the presence of bi-directional casual relationship. Bekiros and Diks [20] also investigated the linear and nonlinear Granger causality linkages between crude oil spot and futures prices and they found strong linear and nonlinear causality relationships. Mamatzakis and Remoundos [21] investigated the nonlinearity in the BRENT crude oil spot and futures price relationships by using a threshold vector error correction model.
Although many studies have examined the inter-temporal causal relationship between commodity spot and futures prices with the objective of examining issues such as price discovery and market efficiency, it is important to notice that previous studies analyse the data at their original level (time domain) and provide a one-shot measure of causal relationship which is supposed to apply across all periodicities. Further, studies evaluating the extent, strength and direction of causality across time and frequency domains leading to a complete inter-fre- quency characterization of the causality are almost non-existent. However, in a purely competitive market, information about direction, strength and extent of such inter-temporal causal relationship is very crucial for the commodity market participants for an effective financial risk management through arbitraging and hedging. In order to overcome this predicament, the present study examines the inter-temporal causal nexus between Indian commodity futures and spot prices by using wavelet based analysis.
The motive behind selecting Indian commodity market under study is due to several reasons. First, after the establishment of national-level commodity exchanges in the year 2003, the growth of Indian commodity futures markets has drastically increased in terms of turnover, number of products, participants, spatial distribution and volume of trade. Secondly, the leading commodity exchange in India, the Multi Commodity Exchange (MCX), is not only number one in India but has also achieved some global milestones. According to Futures Industry Association (FIA) Annual Volume Survey, globally, MCX is first in silver and gold futures; second in copper and natural gas futures and third in crude oil futures1. Thirdly, since India is either one of the major producers or consumers of many commodities and its growing global presence as a fast emerging market, examining the efficiency of Indian commodity futures market is of paramount importance to various stakeholders of commodities markets such as producers, traders, commission agents, commodity exchange’s participants, regulators and policy makers. To the best of our knowledge, this study is the first that examines the inter-temporal causal relationships between commodity spot and futures prices by using wavelet analysis. The application of wavelet analysis enables us to examine the inter-temporal causal relationship between commodity spot and futures prices in the time as well as frequency domains, providing a deeper understanding of direction, strength and extent of such inter-temporal causal relationship.
More specifically, the transformation of data by wavelet transform provides us more insight into the dynamics of economic/financial time series and several dynamic features such as non-stationarity, multi-resolution and approximate de-correlation emerges from wavelet filters. Thus, wavelet filtering provides a natural platform to deal with the time-varying characteristics found in most real-world time series, and thus the assumption of stationarity may be avoided. As a result, wavelet analysis has significant advantages over basic Fourier analysis2 when the object under study is locally stationary and inhomogeneous (Percival and Walden [22] ; Ramsay [23] ). It is important to appreciate that economic/financial time series may not need to follow the same relationship as a function of time horizon (scale). Hence, a transform that decomposes a process into different time horizons is appealing as it differentiates seasonalities, reveals structural breaks and volatility clusters, and identifies local and global dynamic properties of a process at these timescales (Gençay et al. [24] ). Thus, wavelet transform intelligently adapts itself to capture features across a wide range of frequencies and events that are local in time. This makes the wavelet transform an ideal tool for studying non-stationary time series (Fan and Gençay [25] ).
Further, wavelet transform of the data may bring more insights into the existence and nature of highly heterogeneous market participants who do trading at different frequencies. According to heterogeneous market hypothesis, the market participants like speculators, hedgers, market makers etc. differ in terms of expectations, beliefs, risk profiles, informational sets and many others aspects. This market heterogeneity leads to the presence of diverse dealing frequencies and thus, different reactions to the same news in the same market. Each market component has its own reaction time to information, related to its time horizon and dealing frequency characteristic (Dacorogna et al. [26] ). Given its ability to filter the financial time series and modelling financial market heterogeneity, wavelet approach is considered as the most effective tool. In the present study, the continuous wavelet analysis tool (wavelet coherence) is used for measuring the degree of inter-temporal causal relationships between commodity spot and futures prices in the time-frequency domain. It may be interesting to study how the correlations develop in time and also to examine whether the dependencies vary across different frequencies, i.e., if there are stronger dependencies in the longer or shorter investment horizons. In other words, continuous wavelet analysis helps to unravel local correlation and local causal relationship over different time periods and frequencies without relying on traditional econometric techniques.
2. Model and Empirical Approach
2.1. The Continuous Wavelets Transform (CWT)
The objective of the wavelet analysis is to determine the frequency content of a variable with a view to extracting the temporal variation of this frequency content (Heil and Walnut [27] ; Labat [28] ). A wavelet is a function with zero mean localized in both time and frequency. It grows quickly and decays within a limited period (Fan and Gançey [25] ) thereby obeying the conditions that 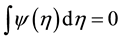 and
and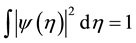 . A wavelet can be characterized by its localization in time
. A wavelet can be characterized by its localization in time  and frequency (
and frequency ( or the bandwidth).
or the bandwidth).
Thus, for a CWT of series 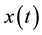
 (1)
(1)
where 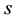 and
and 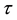 are the scale and location parameters and
are the scale and location parameters and 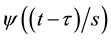 is known as the mother wavelet function that is possibly complex-valued. The symbol
is known as the mother wavelet function that is possibly complex-valued. The symbol 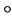 is the convolution operator. A complex wavelet function is of valuable utility in economic analysis as it gives information on local phase. One such function having this property is the Morlet wavelet function. Besides, the Morlet wavelet function can be shown to achieve an optimal localization between the resolution in time and in frequency due to its Gaussian envelop. This property is guaranteed by Heisenberg’s uncertainty theorem stating that there is a lower limit to the product of time and frequency resolution. Also implying a trade-off between the resolution in time and in frequency, the theorem ensures that any improvement in time degrades the frequency resolution and any improvement in frequency degrades the time resolution. Thus, to achieve optimal balance, we employ the Morlet wavelet function given by
is the convolution operator. A complex wavelet function is of valuable utility in economic analysis as it gives information on local phase. One such function having this property is the Morlet wavelet function. Besides, the Morlet wavelet function can be shown to achieve an optimal localization between the resolution in time and in frequency due to its Gaussian envelop. This property is guaranteed by Heisenberg’s uncertainty theorem stating that there is a lower limit to the product of time and frequency resolution. Also implying a trade-off between the resolution in time and in frequency, the theorem ensures that any improvement in time degrades the frequency resolution and any improvement in frequency degrades the time resolution. Thus, to achieve optimal balance, we employ the Morlet wavelet function given by
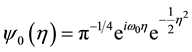 (2)
(2)
where  is dimensionless frequency and
is dimensionless frequency and  is dimensionless time. For optimal balance, we set
is dimensionless time. For optimal balance, we set 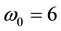 as suggested by Torrence and Compo [29] . Since the idea behind the CWT is to apply the wavelet as a band pass filter to the time series, the wavelet is stretched in time by varying its scale
as suggested by Torrence and Compo [29] . Since the idea behind the CWT is to apply the wavelet as a band pass filter to the time series, the wavelet is stretched in time by varying its scale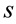 , so that
, so that 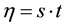 and normalizing it to have unit energy. For the Morlet wavelet, the Fourier period
and normalizing it to have unit energy. For the Morlet wavelet, the Fourier period 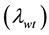

The discretized version of Equation (1) for time series 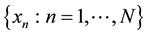
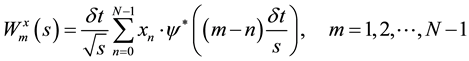
where 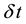
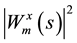
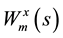
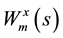
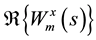
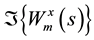
angle, 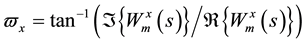
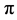
from edge effects caused by a discontinuity at the edge because wavelet is not completely localized in time. To cope with this challenge, the cone of influence (COI) has been introduced. The COI earmarks the area where edge effects cannot be ignored and determines the set of CWT coefficients influenced by the value of the signal at a specified position. Outside COI, edge effects are predominant and can distort the result. Here, the COI is taken as the area in which the wavelet power drops to 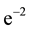
2.2. Wavelet Coherence (WTC)
Since the objective is to measure the extent of synchronization between two given time series, it is informative to measure the coherence between them. Wavelet coherence is a time-frequency counterpart of the time-domain coefficient of determination and shares property with traditional correlation coefficient. As in the Fourier spectral approaches, Wavelet Coherence (WTC) can be defined as the ratio of the cross-spectrum to the product of the spectrum of each series, and can be thought of as the local correlation, both in time and frequency, between two time series (Aguiar-Conraria et al. [30] ). Thus, WTC near one shows a high similarity between the time series, while coherency near zero shows no relationship. While the wavelet power spectrum depicts the variance of a time-series, with times of large variance showing large power, the cross wavelet power of two time-series depicts the covariance between these time-series at each scale or frequency. Following Torrence and Webster (1999), we define the wavelet coherence between two time series as
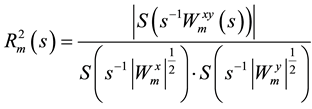
where 
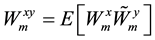



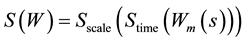
where 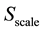
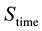

where
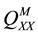
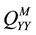

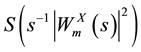
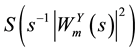

model was used in Ng and Chan [31] and is a specific form of the multivariate case, where the effects of all other variables are removed from the coherence between 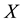

2.3. Significance Level and Background Noise of the Distribution
The statistical significance of wavelet power spectrum of the observed time series can be assessed relative to the null hypothesis that the signal generating the process is stationary. Since the series in this study cannot be said to be stationary at level, stationarity is induced by log-differencing. This transformation ensures that the observed time series is normal and can be modeled as a Gaussian AR (1) process. It is assumed that null hypothesis for power spectrum is normally distributed as AR (1) process. This assumption affects the acceptance of null hypothesis for the power spectrum of each time series or for the co-spectrum of any two time series as well as their coherence. The color of the noise on the other hand is important for both the spectrum and the co-spectrum while the wavelet coherence is insensitive to the choice of the color. Appendix 1 shows that red noise is an appropriate background to test against the theoretical AR (1) spectrum for the power decay closely matching the observed spectrum. The following simple AR (1) model will serve to illustrate the difference between white and red noise
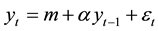
where
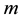
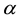
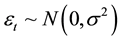
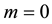
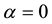
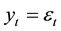
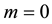
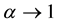

where 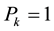
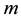
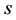
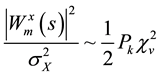
where 


where 
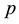
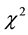
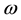
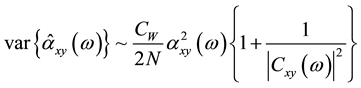
This result is an important demonstration of the relationship between the variability of the cross-amplitude estimate and the coherence of the series. It shows that at all frequencies where coherence is low; the estimate of the cross-amplitude may have an extremely large variance [32] . It is observed that this analogy may well be true of wavelet cross spectrum as well. Aside from this insight into the noted relationship, this conclusion has no damaging implication for the distribution in Equation (10) or for our results. For testing the statistical significance of results, Monte Carlo simulation approach is used and ARMA (1, 0) background noise is used to imitate the red noise. Again, it is important to mention that wavelet coherence is insensitive to the noise colour and the choice of background colour may not affect the result reported for coherence.
3. Data
The data sets used in this study are daily spot and futures closing price series of eight commodities namely gold, silver, crude oil, natural gas, aluminium, copper, chana and soybean, covering the period between 2nd January, 2006 and 31st December, 2014. The categories of commodities under the study are bullion, energy, metals and agricultural commodities. From each category, two top actively trading commodities are selected for the study. The prices of all commodities are collected from the website of MCX except chana and soybean. The prices of chana and soybean are collected from the website of National Commodity and Derivatives Exchange (NCDEX) because among the national level commodity exchanges, NCDEX leads in trading of these agricultural commodities. Both MCX and NCDEX account for more than 90 percentage of the total turnover on all the commodity exchanges in India.
In order to construct the futures price series, the nearby futures contracts are used because these are highly liquid and the most active contracts. Instead of splicing together the nearby futures contracts observations at or near the last trading day, the study employs a different splicing method. First, the nearby futures contract, which is a contract with the nearest active trading delivery month to the day of trading, is specified. Then based on consistent and objective criteria, trading activity3 is taken as the parameter for splicing the price series. Whenever a contract approaches maturity, the market changes its attention away from the nearby month contract to the next nearby contract before the nearby contract approaches its last trading day. It is important to notice that trading volume and open interest for a particular contract peak three or four weeks prior to the last trading day and start declining. The present method evades using observations near the maturity date of the contracts, which represent weakening and wobbly market interest. The criterion established to identify the shift from the nearby contract observations to the next nearby contract is based on when both the daily trading volume and open interest for the next nearby contract surpass those for the nearby contract; it is considered as the evidence of shifting market’s attention from the nearby contract4. At this point we roll-over the series to the next nearby contract.
4. Empirical Results and Discussions
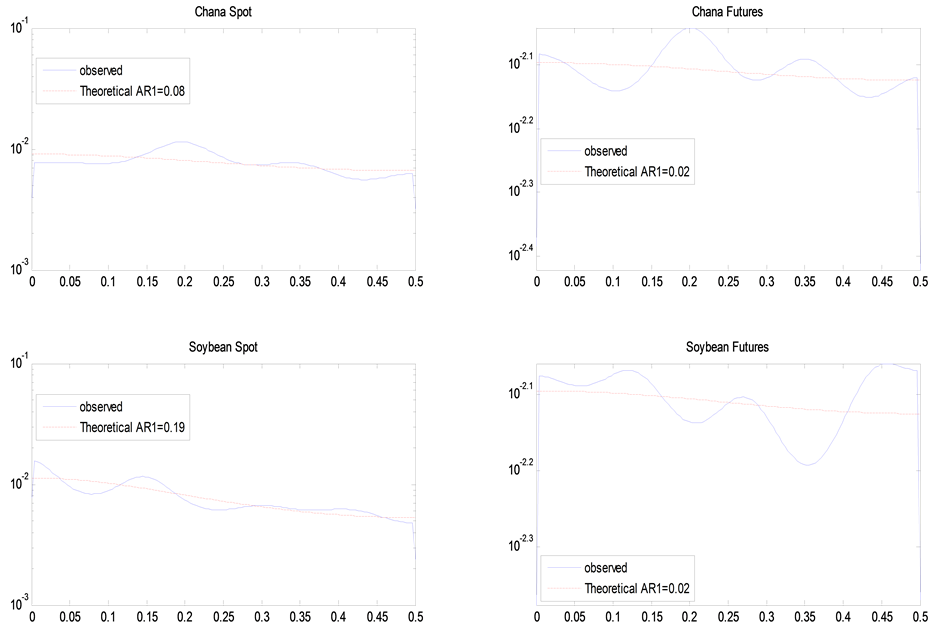
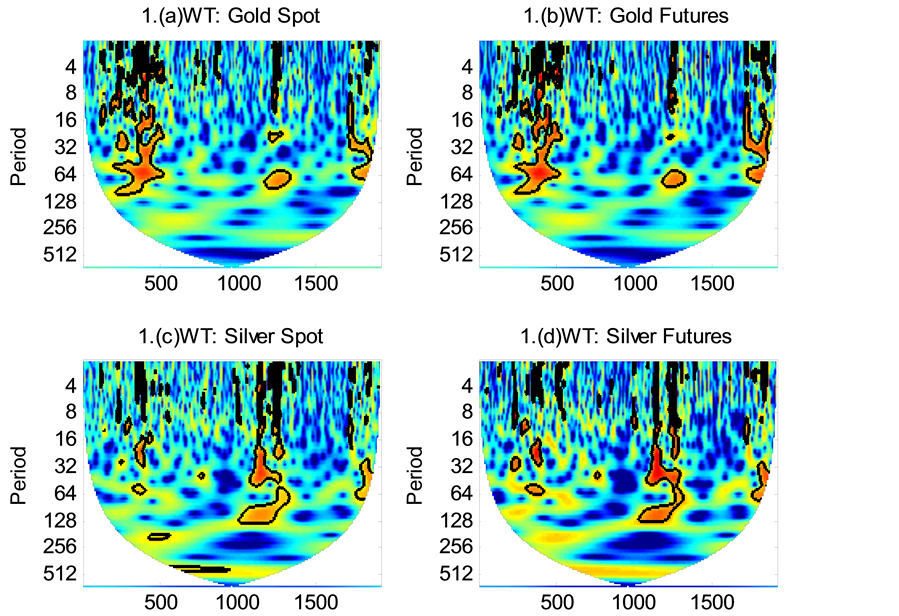
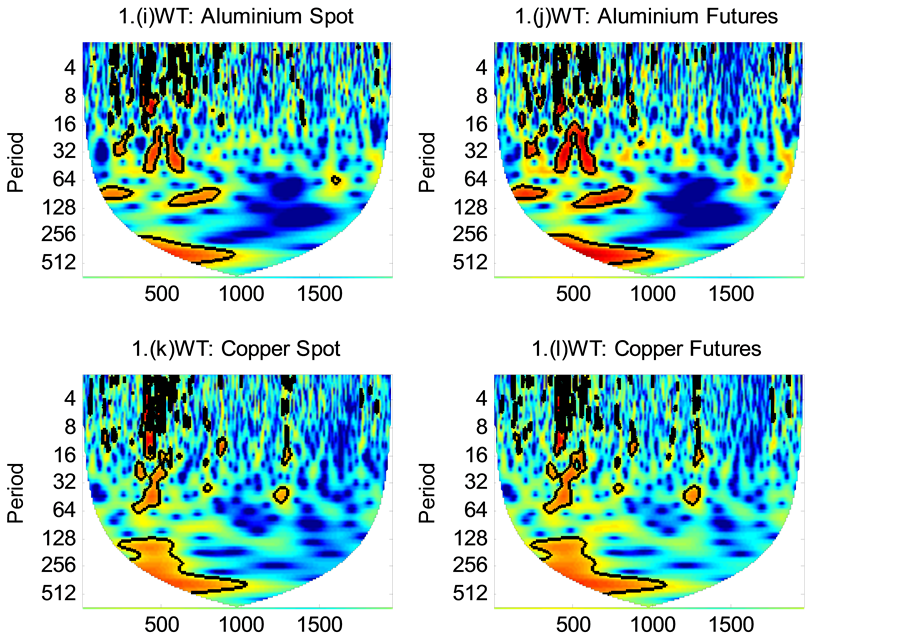
This section deals with the results based on the wavelet analysis. Power decay of the observed and the theoretical spectrums are shown in the Appendix 1 and the continuous wavelet power spectrums measure the volatility or variance of a variable (i.e., the futures and spot prices) in the time-scale space and these are shown in Appendix 2. The horizontal axis measures the time period studied, in terms of the number of days; while the vertical axis indicates frequencies or scales. The colour code for power ranges from blue (low power) to red (high power). In order to facilitate comparison across frequency periods and between time series, the wavelet power has been normalized. Areas with different shades, surrounded by contour curves, show normalized variances. A close observation of wavelet power spectrums indicates that the variance vanishing as the frequency period expands vertically downwards beyond 16 to 20 days. As the frequency periods expand further, or stretches vertically downward, the variance rises again. It is interesting to observe that there are some common islands (common features) in the wavelet power spectrum of spot and futures prices of all commodities except for natural gas and chana. Comparing these patterns of volatility lead towards the question of whether the volatility of one series leads that of another or merely a coincidence. In other words, could the volatility of futures prices lead that of spot prices and vice versa? As an attempt to answer this question, wavelet coherence has been used.
Wavelet coherence analysis provides a complex insight into this dynamics. As mentioned in the methodology section, wavelet coherence measures the local correlation between two time series as a function of frequency, with a value between 0 and 1. When the value is 1, the two series, futures and spot, are perfectly correlated at a particular frequency over a specific period. On the other hand, with a value of 0, there is no local correlation between two series at that particular frequency. Figure 1 shows the estimated wavelet coherence for all the
Figure 1. Wavelet coherence of gold, silver, crude oil, natural gas, aluminium, copper, chana and soybean pairs (futures and spot). The thick black contour designates the 5% significance level against red noise which estimated from Monte Carlo simulations using phase randomized surrogate series. The horizontal axis shows time, while the vertical axis shows the period in days. The phase difference between the two series is indicated by arrows. Arrows pointing to the right mean that the series are in phase. To the right and up, mean that futures price is leading. To the right and down, means that futures price is lagging. Arrows pointing to the left mean that the variables are out of phase. To the left and up, mean that spot price is leading. To the left and down, mean that spot price is lagging.
commodities examined. Time is shown on the x-axis, while the y-axis refers to frequency; the lower the frequency, the higher the scale. The convex curve stretching from the left margin to the right margin is the cone of influence, where the area beyond which is statistically insignificant.
Regions plotted in red colour represent areas with significant dependence. The darker is the shade within a contoured area, the higher the coherence. The lighter the colour is, suggests that the coherence is lower than 0.5, the less dependent the series are. Thus, we can clearly perceive both the frequency and the time intervals where the futures and spot prices move together significantly. The black regions in the high frequency area in Figure 1 depict that the two series are often locally correlated. When futures and spot prices are in-phase the directional arrows point to the right; on the other hand, arrows pointing to the left indicate that the two data series are completely out of phase with each other. An arrow pointing up indicates that futures prices lead spot prices whereas arrows pointing down indicate that spot prices lead futures prices. In case of almost all commodities under study, close to 16 days, the arrows are pointing right and up indicate that futures price leads spot price. In other words, there is a uni-directional temporal causal relationship exists from futures market to spot market during this period and indicates that futures market performs the price discovery function. Moreover, the arrows beyond frequency band higher than 16 days point to the right most of the time, suggest significant local correlations between futures and spot prices. There are short periods in which futures and spot prices seem to be leading each other. But, it is difficult to conclude that there is any bi-directional influence always because these trends are not consistent.
5. Conclusion
The novelty of this study lies in the application of wavelet analysis to study the inter-temporal causal relationship between commodity spot and futures prices in order to provide more insights into the direction, strength and extent of such inter-temporal causal relationship. Wavelet analysis offers an effective alternative tool by analysing the data in both time and frequency domain, whereas in traditional econometric causality analysis tools focus only on the time domain. Moreover, this technique is more appropriate for processing non-stationary data because it does not necessitate a time series to meet a stationarity requirement. Daily futures and spot price series on eight commodities like gold, silver, crude oil, natural gas, aluminium, copper, chana and soybean from the Indian commodity exchanges (MCX and NCDEX) were examined for the period 2nd January, 2006 to 31st December, 2014. The result of wavelet coherence analysis suggests that there is a strong uni-directional temporal causal relationship exists from futures market to spot market close to a frequency band of 16 days in case of almost all the selected commodities under the study. Moreover, the results suggest that in long term, futures and spot price series move together in phase with each other most of the time. This indicates that futures market has a powerful price discovery function in all the selected commodities; which in turn indicates the efficiency of Indian commodity futures market. Even though the study gives an extensive direction for policymakers and researchers, results from data collected at much higher frequencies would be exceptionally useful for policy makers, researchers and market participants. The use of intraday tick-by-tick data might be providing more robust results. The analysis of this study is based on daily closing price and it is calculated as the average of prices in the last half hour of trade in the market.
References
- Garbade, K. and Silber, W.L. (1983) Price Movement and Price Discovery in Futures and Cash Markets. The Review of Economics and Statistics, 65, 289-297. http://dx.doi.org/10.2307/1924495
- Oellermann, C.M., Brorsen, B.W. and Farris, P.L. (1989) Price Discovery for Feeder Cattle. The Journal of Futures Markets, 9, 113-121. http://dx.doi.org/10.1002/fut.3990090204
- Schroeder, T.C. and Goodwin, B.K. (1991) Price Discovery and Cointegration for Live Hogs. The Journal of Futures Markets, 11, 685-696. http://dx.doi.org/10.1002/fut.3990110604
- Koontz, S.R., Garcia, P. and Hudson, M.A. (1990) Dominant-Satellite Relationship between Live Cattle Cash and Futures Markets. Journal of Futures Markets, 10, 123-136. http://dx.doi.org/10.1002/fut.3990100204
- Geweke, J. (1982) Measurement of Linear Dependence and Feedback between Multiple Time Series. Journal of the American Statistical Association, 77, 304-324. http://dx.doi.org/10.1080/01621459.1982.10477803
- Iyer, V. and Pillai, A. (2010) Price Discovery and Convergence in the Indian Commodities Market. Indian Growth and Development Review, 3, 53-61. http://dx.doi.org/10.1108/17538251011035873
- Granger, C.W.J. (1986) Developments in the Study of Cointegrated Economic Variables. Oxford Bulletin of Economics and Statistics, 48, 213-228. http://dx.doi.org/10.1111/j.1468-0084.1986.mp48003002.x
- Engle, R.F. and Granger, C.W. (1987) Cointegration and Error Correction: Representation, Estimation and Testing. Econometrica, 55, 251-276. http://dx.doi.org/10.2307/1913236
- Johansen, S. (1988) Statistical Analysis of Cointegration Vectors. Journal of Economic Dynamics and Control, 12, 231-254. http://dx.doi.org/10.1016/0165-1889(88)90041-3
- Serletis, A. and Banack, D. (1990) Market Efficiency and Cointegration: An Application to Petroleum Market. Review of Futures Markets, 9, 372-385.
- Crowder, W.J. and Hamed, A. (1993) A Cointegration Test for Oil Futures Market Efficiency. The Journal of Futures Markets, 13, 933-941. http://dx.doi.org/10.1002/fut.3990130810
- Schwarz, T.V. and Szakmary, A.C. (1994) Price Discovery in Petroleum Markets: Arbitrage, Cointegration, and the Time Interval of Analysis. The Journal of Futures Markets, 14, 147-167. http://dx.doi.org/10.1002/fut.3990140204
- Chowdhury, A.R. (1991) Futures Market Efficiency: Evidence from Cointegration Tests. The Journal of Futures Markets, 11, 577-589. http://dx.doi.org/10.1002/fut.3990110506
- Beck, S. (1994) Cointegration and Market Efficiency in Commodities Futures Markets. Applied Economics, 26, 249- 257. http://dx.doi.org/10.1080/00036849400000006
- McKenzie, A.M. and Holt, M.T. (2002) Market Efficiency in Agricultural Futures Markets. Applied Economics, 34, 1519-1532. http://dx.doi.org/10.1080/00036840110102761
- Savit, R. (1988) When Random Is Not Random: An Introduction to Chaos in Market Prices. The Journal of Futures Markets, 8, 271-290. http://dx.doi.org/10.1002/fut.3990080303
- Savit, R. (1989) Nonlinearities and Chaotic Effects in Option Prices. The Journal of Futures Markets, 9, 507-518. http://dx.doi.org/10.1002/fut.3990090604
- Abhyankar, A. (1996) Does the Stock Index Futures Market Tend to Lead the Cash? New Evidence from the FT-SE 100 Stock Index Futures Market. Working Paper No. 96-01, Department of Accounting and Finance, University of Stirling, Stirling.
- Silvapulle, P. and Moosa, I.A. (1999) The Relationship between Spot and Futures Prices: Evidence from the Crude Oil Market. The Journal of Futures Markets, 19,175-193. http://dx.doi.org/10.1002/(SICI)1096-9934(199904)19:2<175::AID-FUT3>3.0.CO;2-H
- Bekiros, S.D. and Diks, C.G. (2008) The Relationship between Crude Oil Spot and Futures Prices: Cointegration, Linear and Nonlinear Causality. Energy Economics, 30, 2673-2685. http://dx.doi.org/10.1016/j.eneco.2008.03.006
- Mamatzakis, E. and Remoundos, P. (2011) Testing for Adjustment Costs and Regime Shifts in BRENT Crude Oil Futures Market. Economic Modelling, 28, 1000-1008. http://dx.doi.org/10.1016/j.econmod.2010.11.008
- Percival, D.B. and Walden, A.T. (2000) Wavelet Methods for Time Series Analysis. Cambridge Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511841040
- Ramsay, J.B. (2002) Wavelets in Economics and Finance: Past and Future. Studies in Nonlinear Dynamics and Econometrics, 6, 514-539. http://dx.doi.org/10.2202/1558-3708.1090
- Gençay, R., Selçuk, F. and Whitcher, B. (2002) An Introduction to Wavelets and Other Filtering Methods in Finance and Economics. Academic Press, Waltham.
- Fan, Y. and Gençay, R. (2010) Unit Root Tests with Wavelets. Econometric Theory, 26, 1305-1331. http://dx.doi.org/10.1017/S0266466609990594
- Dacorogna, M., Gençay, R., Muller, U., Olsen, R. and Pictet, V. (2001) An Introduction to High-Frequency Finance. Academic Press, San Diego.
- Heil, C.E. and Walnut, D.F. (1989) Continuous and Discrete Wavelet Transforms. SIAM Review, 31, 628-666. http://dx.doi.org/10.1137/1031129
- Labat, D. (2005) Recent Advances in Wavelet Analyses: A Review of Concepts. Journal of Hydrology, 314, 275-288. http://dx.doi.org/10.1016/j.jhydrol.2005.04.003
- Torrence, C. and Compo, G.P. (1998) A Practical Guide to Wavelet Analysis. Bulletin of the American Meteorological Society, 79, 605-618. http://dx.doi.org/10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2
- Aguiar-Conraria, L. and Soares, M.J. (2011) Oil and the Macro Economy: Using Wavelets to Analyze Old Issues. Empirical Economics, 40, 645-655. http://dx.doi.org/10.1007/s00181-010-0371-x
- Ng, E.K.W. and Chan, J.C.L. (2012) Geophysical Applications of Partial Wavelet Coherence and Multiple Wavelet Coherence. Journal of Atmospheric and Oceanic Technology, 29, 1845-1853. http://dx.doi.org/10.1175/JTECH-D-12-00056.1
- Priestley, M.B. (1981) Spectral Analysis and Time Series. Academic Press, London.
- Ripple, R.D. and Moosa, I.A. (2009) The Effect of Maturity, Trading Volume and Open Interest on Crude Oil Futures Price Range-Based Volatility. Global Finance Journal, 20, 209-219. http://dx.doi.org/10.1016/j.gfj.2009.06.001
Appendix 1: Power Decay of the Observed and the Theoretical Spectrum
Appendix 2: The Continuous Wavelet Power Spectrum of Both Spot and Futures
NOTES
*Corresponding author.
1For contracts traded during the calendar year 2013.
2Fan and Gençay ([25] , p. 1307) documented that, “The Fourier approach is appealing when working with stationary time series. However, restricting ourselves to stationary time series is not appealing, since most economic/financial time series exhibit quite complicated patterns over time (e.g., trends, abrupt changes, and volatility clustering). In fact, if the frequency components are not stationary such that they may appear, disappear, and then reappear over time, traditional spectral tools may miss such frequency components.”
3Trading activity includes both volume and open interest, which are considered as the representative of the focus of the market, information flow and market depth (Ripple and Moosa [33] ).
4We consistently observed that once both conditions are met, the near-month contract never revert back to the focus of trading activity.