Theoretical Economics Letters
Vol. 2 No. 3 (2012) , Article ID: 21519 , 4 pages DOI:10.4236/tel.2012.23061
Academic Crossover and Functional Differentiation of Universities
Research Institute for Higher Education, Hiroshima University, Hiroshima, Japan
Email: {yasumi, sw259}@hiroshima-u.ac.jp
Received May 27, 2012; revised June 28, 2012; accepted July 27, 2012
Keywords: Academic Crossover; Functional Differentiation; Resource Allocation; University Prestige
ABSTRACT
This study is motivated by a theoretical deficiency in the research on internal resource allocation and functional differentiation of higher education institutions in relation with their prestige maximizing behaviors. Our finding, despite its purely theoretical nature, suggests that a prestige-maximizing college or university achieves the highest potential prestige by optimally allocating its limited resources and equalizing the prestige of the closely associated academic departments or disciplines. The result certainly indicates that the interdisciplinary activities and functional differentiation, which represent two major efforts found in the recent higher education community, have indeed counteractive effects on their separate objectives.
1. Introduction
Academic crossover as typified by interdisciplinary research and learning have contributed tremendously to the creation of new knowledge in nearly every aspect of today’s multifaceted human activities. At large research universities in the US, internal resources are strategically allocated to encourage such cross-disciplinary activities to further enhance collaborative research and development. Yet, another noteworthy trend found in an increasingly diverse higher education environment is the rising importance of differentiating institutions with regard to their missions or functions (Gumport and Bastedo [1]). For instance, state-funded colleges and universities with multiple campuses in the US are often concerned about the cost-effectiveness of their regional system in funding redundant academic instruction and research activities (Nelms et al. [2]). A vital question from the perspectives of public finance and higher education policy, then, is whether or not these two forces, i.e., academic crossover and mission differentiation, produce synergetic effects that enhance, or counteractive effects to impede, the attainment of their separate objectives.
A theoretical foundation laid by Abe and Watanabe [3, 4] provides a mechanism which helps us understand optimizing behaviors of colleges and universities with regard to internal resource allocation and maximization of institutional prestige. Abe and Watanabe [5], using the same analytic apparatuses further show that different institutional funding schemes could cause different impacts on the extent to which functional differentiation is achieved by colleges and universities. However, the theoretical model developed by Abe and Watanabe hinges on an additively separable form of prestige functions, for which each institution of higher education is considered to simply maximize the sum total of prestige, earned independently in separate academic disciplines and/or functional activities offered by the institution. The additive separability is an unattractive feature for the analysis, particularly if different academic disciplines, e.g., economics, physics, and psychology, contribute non-negligibly through combined efforts to new knowledge production, which in turn leads to enhancement of academic strengths and eventually of overall institutional prestige.
This study is motivated by the theoretical deficiency in the relevant research and addresses the issue by explicitly incorporating the correlation potentially existing between different academic disciplines. Our main finding suggests that academic overlapping across multiple disciplines within an institution yield a neutralizing effect on the focus of the involved fields. That is, the result indicates that collaborative efforts involving multiple departments could impede functional differentiation of higher education institutions.
2. Basic Framework
Preceding studies exist in the literature, which perceive the industry of higher education as a marketplace where individual colleges and universities, acting as prestige or reputation maximizers, offer multiple products and services such as student instruction, research output, and community services, for their stakeholders which include students, alumni, communities, and governments (Baumol et al. [6], Breneman [7], Brewer et al. [8], Cyrenne and Grant [9], Del Rey [10]). Abe and Watanabe [3,4], in particular, demonstrate a mechanism through which optimal allocation arrangement of resources is sought by an institution of higher education in pursuit of the highest institutional prestige. The proposed model conceives the total prestige of an institution as the sum of the partial prestige collected from each field 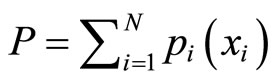 where
where
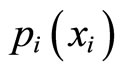 represents partial prestige independently earned in disciplines
represents partial prestige independently earned in disciplines , with xi being the corresponding financial resource input. We assume
, with xi being the corresponding financial resource input. We assume  and that an institution allocates its limited resources
and that an institution allocates its limited resources
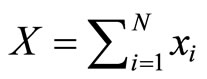 so as to maximize its overall prestige. Although the findings by Abe and Watanabe contribute to a fundamental understanding with regard to internal resource allocation and attainable prestige for colleges and universities, the additive separability of the prestige function certainly limits its full applicability, particularly when collaborative work by multiple departments jointly produce synergizing effects on the enhancement of institutional strengths.
so as to maximize its overall prestige. Although the findings by Abe and Watanabe contribute to a fundamental understanding with regard to internal resource allocation and attainable prestige for colleges and universities, the additive separability of the prestige function certainly limits its full applicability, particularly when collaborative work by multiple departments jointly produce synergizing effects on the enhancement of institutional strengths.
Assume instead that a university attempts to maximize a more generalized form of prestige function , which is not necessarily an additive separable function of
, which is not necessarily an additive separable function of  and satisfies
and satisfies 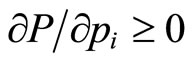 for
for . The optimization problem is simply formulated as
. The optimization problem is simply formulated as
 subject to
subject to  (1)
(1)
with the required optimality conditions
 (2)
(2)
 (3)
(3)
for . Then, it is an elementary matter that the solution is graphically presented where the possible prestige hypersurface, represented by a vector
. Then, it is an elementary matter that the solution is graphically presented where the possible prestige hypersurface, represented by a vector
 , and the iso-prestige hypersurface
, and the iso-prestige hypersurface , are tangent with each other, for a given level of financial resources
, are tangent with each other, for a given level of financial resources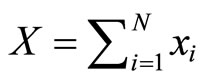 .
.
In contrast to solving the optimization problem with the additively separable prestige function, an obvious difficulty with the problem (1) is brought out by 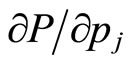 in the first-order condition (2) which may in general involve partial prestige
in the first-order condition (2) which may in general involve partial prestige 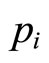 in fields
in fields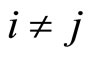 . In order to cope with the technical difficulty, we note that the possible prestige hypersurface
. In order to cope with the technical difficulty, we note that the possible prestige hypersurface 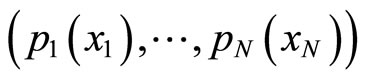 is drawn solely with allocation dependency and is not affected by the functional form of
is drawn solely with allocation dependency and is not affected by the functional form of . That is, the effect of changing allocation arrangement
. That is, the effect of changing allocation arrangement  is captured by the possible prestige hypersurface, whereas the effect of the change in the functional form of the prestige function
is captured by the possible prestige hypersurface, whereas the effect of the change in the functional form of the prestige function  is captured by the iso-prestige hypersurface. Thus, the effects of these two changes on the optimization may be analyzed and discussed separately.
is captured by the iso-prestige hypersurface. Thus, the effects of these two changes on the optimization may be analyzed and discussed separately.
3. Analysis
We consider, without loss of generality, a heuristically simple case with . The loci of attainable prestige combinations, i.e., possible prestige curve, for a given amount of institutional funding
. The loci of attainable prestige combinations, i.e., possible prestige curve, for a given amount of institutional funding , may be traced by
, may be traced by , whereas the iso-prestige curve is expressed by
, whereas the iso-prestige curve is expressed by 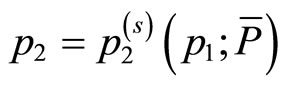 for a fixed level of prestige
for a fixed level of prestige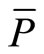 .1 Then, the following identities are satisfied by construction:
.1 Then, the following identities are satisfied by construction:
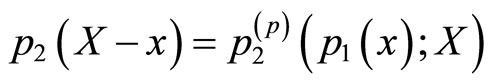 (4)
(4)
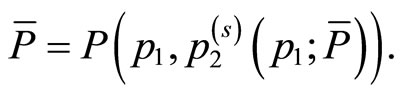 (5)
(5)
Using the identity (4), we derive
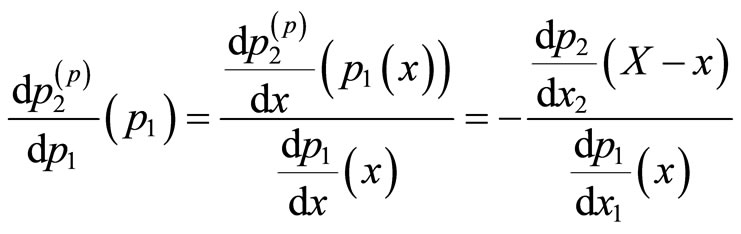 (6)
(6)
from which we obtain 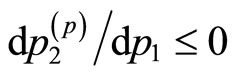 since
since  for
for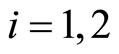 . Similarly, differentiating both sides of the identity (5) with respect to
. Similarly, differentiating both sides of the identity (5) with respect to 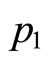 gives
gives
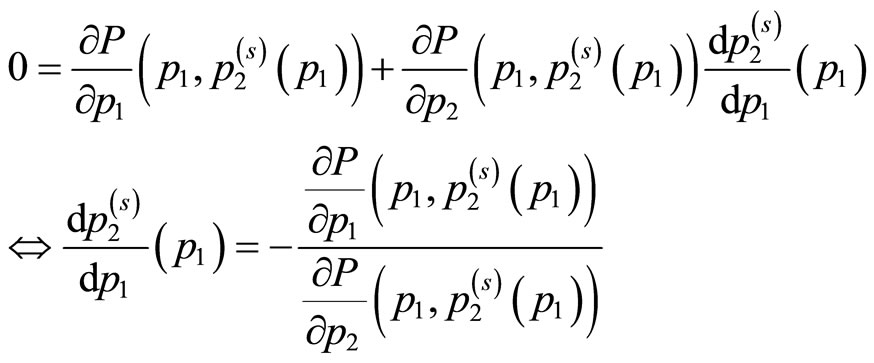 (7)
(7)
which also yields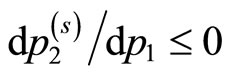 . As the optimization is sought where the two curves are tangent,
. As the optimization is sought where the two curves are tangent,
 (8)
(8)
certainly yielding the same optimality condition as given in Equation (2) above.
Suppose now that the functional form of P is altered slightly from the original form 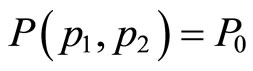 which has an additively separable form of prestige
which has an additively separable form of prestige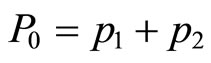 , to a more generalized form
, to a more generalized form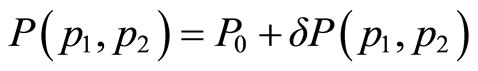 . We then examine the effect of
. We then examine the effect of  to its first-order approximation. The situation is depicted in Figure 1 below. For
to its first-order approximation. The situation is depicted in Figure 1 below. For , the optimality condition at
, the optimality condition at 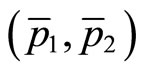
requires  as
as . For
. For
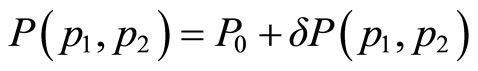 , the maximized prestige is attained at
, the maximized prestige is attained at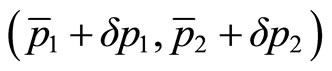 , where the condition requires
, where the condition requires
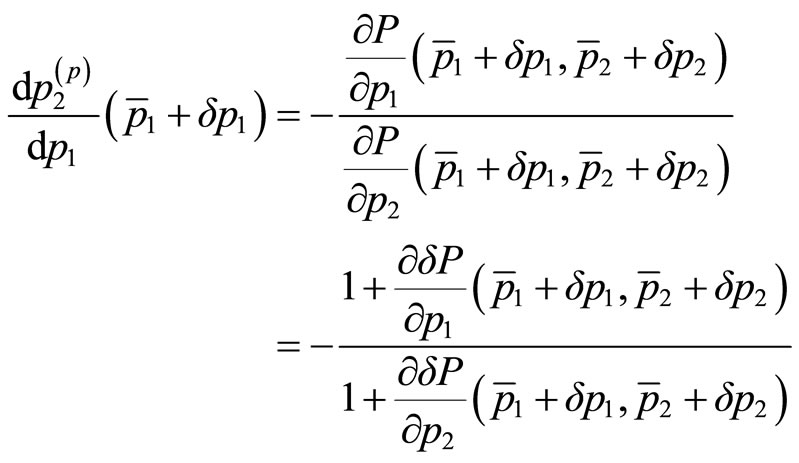 (9)
(9)
The new maximum is attained on the identical possible prestige curve, and the relation between  and
and  is written by
is written by
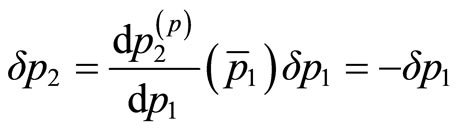 (10)
(10)
Expanding the Equation (9) to the first-order approximation with respect to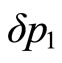 ,
,  , and
, and , and using the result (10) gives
, and using the result (10) gives
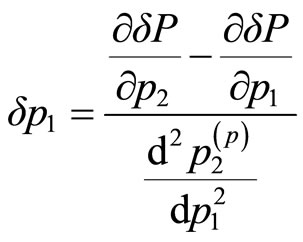 (11)
(11)
The slope of the iso-prestige curve at  is
is
 (12)
(12)
so  may be rewritten as
may be rewritten as
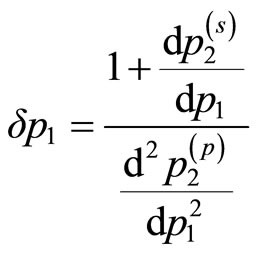 (13)
(13)
Since we have 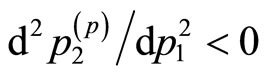 at the maximum
at the maximum , the sign of
, the sign of  is determined by whether the slope of the iso-prestige curve at
is determined by whether the slope of the iso-prestige curve at 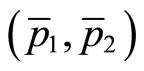 is greater or smaller than –1 after the change in the functional form P. We know with certainty that
is greater or smaller than –1 after the change in the functional form P. We know with certainty that 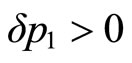 (and
(and 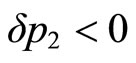 by
by
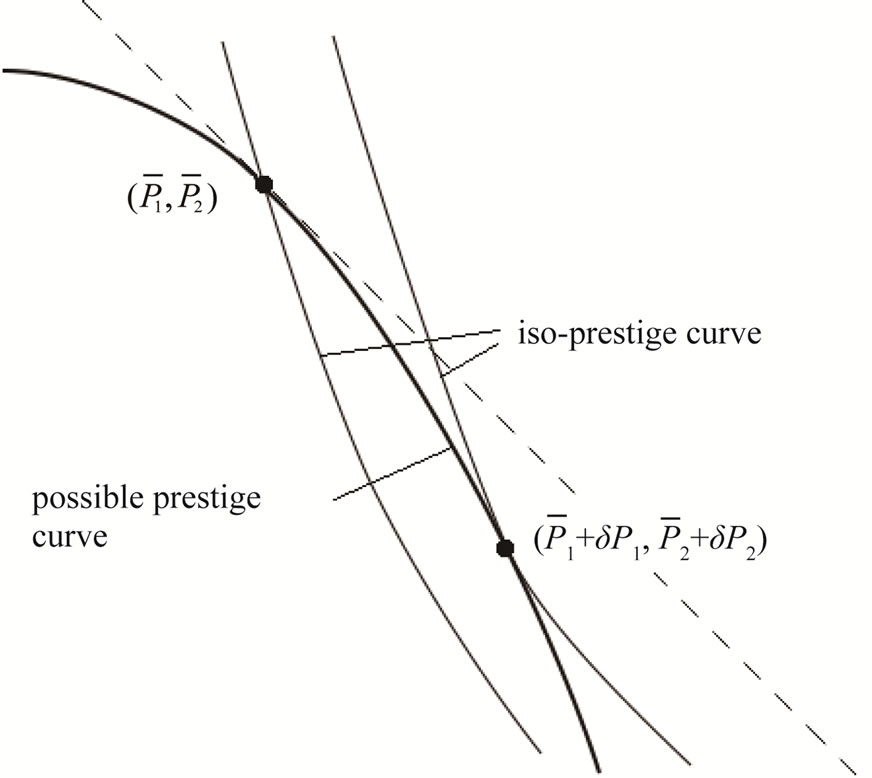
Figure 1. Shift in the optimizing point as a result of a change in the functional form of prestige function.
Equation (10)) if , and
, and 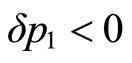 (and
(and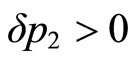 ) for
) for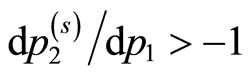 .
.
4. Impact on Functional Differentiation
For a heuristic analysis with N = 2, consider a college with only two academic departments, e.g., economics and physics, maximizing the objective function 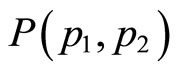 which explicitly involves the correlation term
which explicitly involves the correlation term
 (14)
(14)
The last term  represents the correlation between the two disciplines and is assumed to satisfy 1)
represents the correlation between the two disciplines and is assumed to satisfy 1)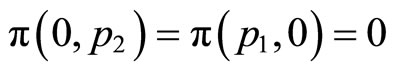 ; 2)
; 2) ; 3) differentiable for an appropriate number of times with respect to
; 3) differentiable for an appropriate number of times with respect to 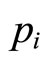 for
for ; and 4)
; and 4) ,
, 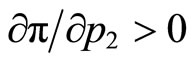 .
.
Using the result in Equation (7),
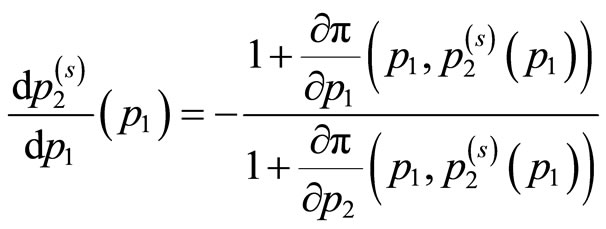 (15)
(15)
yielding . Since
. Since  is symmetric in
is symmetric in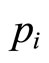 , i.e.,
, i.e., 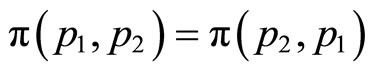 , we have
, we have 
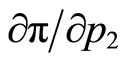 for
for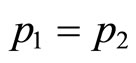 . Therefore, we obtain
. Therefore, we obtain 
 when
when .
.
We consider a situation in which a university encourages cross-disciplinary activities and further assume that 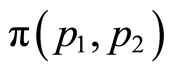 is monotonically decreasing in
is monotonically decreasing in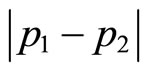 , which means that the correlation term takes larger values as the levels of prestige for the two disciplines become closer. In order to represent this property more precisely, we use the following variables instead of
, which means that the correlation term takes larger values as the levels of prestige for the two disciplines become closer. In order to represent this property more precisely, we use the following variables instead of  and
and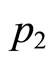 :
:
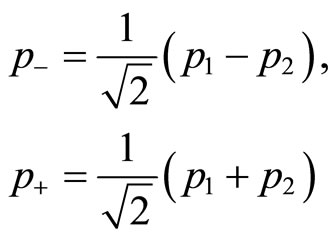 (16)
(16)
In terms of 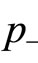 and
and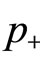 , the above-mentioned condition is given by
, the above-mentioned condition is given by 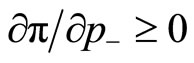 for
for 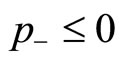 and
and 
for . Since
. Since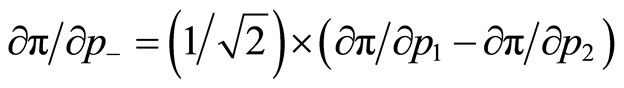 it follows that
it follows that  for
for , and
, and 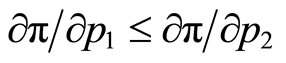 for
for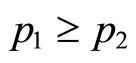 . This indicates in turn that
. This indicates in turn that
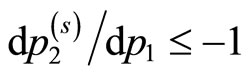 for
for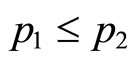 , and
, and 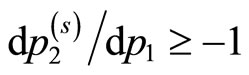 for
for
 .
.
Therefore, combining the result with the finding obtained in the third section, the optimizing solution with correlation is necessarily located closer to the diagonal array  than the optimization attainable by the prestige function without the correlation term. The result indicates that, when the conditions
than the optimization attainable by the prestige function without the correlation term. The result indicates that, when the conditions 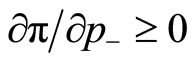 for
for 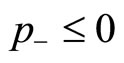 and
and 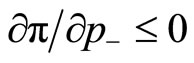 for
for 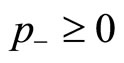 are satisfied,2 a university with two associated academic fields has an incentive to allocate its internal resources so as to gain an equal level of prestige in both fields. Thus, the result suggests that the functional differentiation among universities becomes more difficult when they manage the identical set of correlated disciplines and/or institutional activities than otherwise.
are satisfied,2 a university with two associated academic fields has an incentive to allocate its internal resources so as to gain an equal level of prestige in both fields. Thus, the result suggests that the functional differentiation among universities becomes more difficult when they manage the identical set of correlated disciplines and/or institutional activities than otherwise.
5. Conclusion
This study predicts the potential outcome for an institution with cross-disciplinary overlapping among multiple disciplines/activities with regard to the extent to which functional differentiation is achieved. Our finding, despite its purely theoretical nature, demonstrates that there exists a compelling force for a prestige-maximizing institution to make an internal allocation arrangement so as to gain the equal level of prestige for separate but correlated disciplines/departments. The result certainly indicates that the academic crossover and functional differentiation, which represent two major trends observed in the recent higher education industry, have counteractive effects on the attainment of their separate objectives. The analysis is also readily applicable to other scenarios, such as an institution attempting to differentiate its mission by undergraduate student instruction (e.g., as a liberal arts college) versus placing heavier weights on graduate teaching and faculty research (as a research university). The future agenda certainly involves empirical research with existing data and testing the validity of the proposed model as well as the predicted outcomes.
6. Acknowledgements
The authors would like to thank an anonymous referee for comments and suggestions. The basic concepts and motivation for this study were gained while one of the authors was a visiting scholar at the Center for Studies in Higher Education (CSHE), University of California, Berkeley. We would like to express sincere gratitude for all the encouragement and generous resources provided by CSHE and UC Berkeley.
REFERENCES
- P. J. Gumport and M. N. Bastedo, “Academic Stratification and Endemic Conflict: Remedial Education Policy at CUNY,” The Review of Higher Education, Vol. 24, No. 4, 2001, pp. 333-349. doi:10.1353/rhe.2001.0009
- C. Nelms, K. R. R. G. Louis, F. C. Richardson, M. Roberts, J. Schmit and M. Wilkerson, “Mission Differentiation at Indiana University: Eight Campus Identity, One Shared Destiny,” Final Report of the Mission Differentiation Project, 2005. http://www.indiana.edu/~dema/reports/mdpreport.pdf
- Y. Abe and S. P. Watanabe, “A New Approach to Analyzing University Prestige and Internal Resource Allocation: Geometric Interpretations and Implications,” Research and Occasional Paper Series, University of California, Berkeley, 2012. http://cshe.berkeley.edu/publications/docs/ROPS.Abe&Watanabe.UnivPrestige.6.11.2012.pdf
- Y. Abe and S. P. Watanabe, “A Theory of Optimal Resource Allocation and Prestige Maximization of Universities,” Unpublished Working Paper, 2012.
- Y. Abe and S. P. Watanabe, “The Impact of Different Funding Schemes on Functional Differentiation of Universities,” Unpublished Working Paper, 2012.
- W. J. Baumol, J. C. Panzar and R. D. Willig, “Contestable Markets and the Theory of Industry Structure,” Marcourt Brace Jovanovich, New York, 1982.
- D. W. Breneman, “The Ph.D. Production Process,” In: J. T. Froomkin, D. T. Jamison and R. Radner, Eds., Education as an Industry, National Bureau of Economic Research, Cambridge, 1976, pp. 1-52.
- D. J. Brewer, S. M. Gates and C. A. Goldman, “In Pursuit of Prestige: Strategy and Competition in US Higher Education,” Transaction Publishers, Piscataway, 2001.
- P. Cyrenne and H. Grant, “University Decision Making and Prestige: An Empirical Study,” Economics of Education Review, Vol. 28, No. 2, 2009, pp. 237-248. doi:10.1016/j.econedurev.2008.06.001
- E. Del Rey, “Teaching versus Research: A Model of State University Competition,” Journal of Urban Economics, Vol. 49, No. 2, 2001, pp. 356-373. doi:10.1006/juec.2000.2193
NOTES
1For notational simplification, we denote 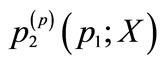 and
and 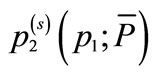 as
as 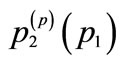 and
and , respectively.
, respectively.
2For example, 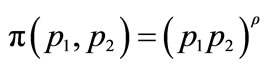 ,
,  satisfies the conditions.
satisfies the conditions.

