Theoretical Economics Letters
Vol. 2 No. 1 (2012) , Article ID: 17385 , 8 pages DOI:10.4236/tel.2012.21019
A Role of Chaotic Phenomenon and the Central Place System in a Firm’s Location Selections
Faculty of Economics, Chuo University, Hachioji, Japan
Email: ishiy@tamacc.chuo-u.ac.jp
Received October 30, 2011; revised November 30, 2011; accepted December 10, 2011
Keywords: Chaotic phenomenon; Central place system; Factory’s location
ABSTRACT
When a manufacturing firm has a plan to build a factory, the determination of the factory’s location site is one of the most important elements in the plan. Since the manufacturer does not have enough information of economic conditions of all potential location sites, the manufacturer cannot determine immediately its location site. A series of steps are taken to determine the location place. The firm makes range of searching area small step by step toward the site determination; 1) Determination of a prospective region in a large space; 2) Selection of a potential area in that region; 3) Choice of an urban district in that area; 4) Decision of a site in the district. This paper proposes that chaotic phenomenon, which is appeared in the calculation processes to specify the optimal location site, may be used to identify a prospective region. And then, it is shown in the paper that the central place systems laid in the region play a role in the selection of a potential area for the factory location. This paper elucidates how a firm searches step by step an appropriate factory’s location within a large geographical area.
1. Introduction
When a manufacturing firm projects to build a factory, the firm determines factory’s location site as well as the quantity and the price of the goods produced in the factory. Once a factory is constructed at a site, the firm will not easily move it to another place since the removing the factory bears enormous costs in many ways. Factory’s location affects the factory management in the long term so that the decision of location is always one of important tasks of the manufacturers.
Viewing the industrial location in these days1, there are two characteristic location trends. One is that firms fragment production processes to some blocs in order to reduce production costs2, and each bloc moves in the long distance to the place that is suitable to its production processes. Another is the trend that high-skilled workers like the places where they make full use of their ability and they move easily to those places. Being influenced by these trends, many factories tend to shift across countries to seek for an optimal place.
Corresponding to the above picture, this paper considers that when firms try to search location for their factories within a large geographical area, firms take a series of steps to determine the location place since they do not have enough information of economic conditions of all potential location sites: The firms make range of searching area small step by step in the site determination processes. The paper firstly proposes that in the first step chaotic phenomenon can be used to identify a prospective region for the possible factory’s location in a large space. Secondly, the paper elucidates a role of the central place system in a firm’s selection of the possible area in the prospective region. As is well known, Christaller [3] and Lösch [4] examine the central place system from the different viewpoints. This paper combines the central place system by Christaller with a factory’s location, and explains how this system influences a firm’s decisionmaking of location.
The paper is organized as follows: Section 2 investigates a factory’s location and price of goods by using the gradient dynamics. In Section 3 the relationships between a factory’s location and the central place system are examined. Section 4 explains four steps which a firm takes in decision-making of location when it chooses a location site in a large spatial area. Section 5 concludes the analysis3.
2. The Role of Chaotic Phenomenon in a Firm’s Decision of Location
2.1. Derivation of a Firm’s Profit
A firm’s profit function is derived on the following assumptions. A factory uses two kinds of raw materials m1, m2 to produce final goods m4. The factory uses an additional material m3 to complete the goods, that is, fuel or lubrication oil are needed to the operating the production processes. The materials m1, m2 and m3 are produced at points M1, M2 and M3 which are identified by coordinates (x1, y1), (x2, y2), (x3, y3), respectively on a large plain space. They are transported to the factory at point L indicated by (x, y). Freight rates of the materials m1, m2 are denoted by tm, and the rate of the material m3 is given by te. Mill prices of these materials are shown by p1, p2, and p3, and these prices are given. The price of the finished good p4 is determined by the firm to maximize the profits. The finished goods are transported from the factory to the market at point M4(x4, y4). The freight rate of the finished goods m4 is tg. Figure 1 illustrates the geographical relationship between the factory, the market and the producing points of the materials.
The factory’s production function is represented by equation (1):
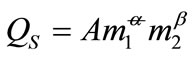 (1)
(1)
where QS is quantity produced. A, α and β are parameters and they are defined as A > 0, 0 < (α + β) < 1. Market demand function for the finished goods is given by equation (2):
 (2)
(2)
where Qd is quantity demanded, a is the maximum reservation price of the finished good. The factory produces just as much goods as the market demands: QS must be equal to Qd. The distances between the producing place Mi (i = 1, 2, 3) and the factory L are represented by d1, d2 d3, respectively:
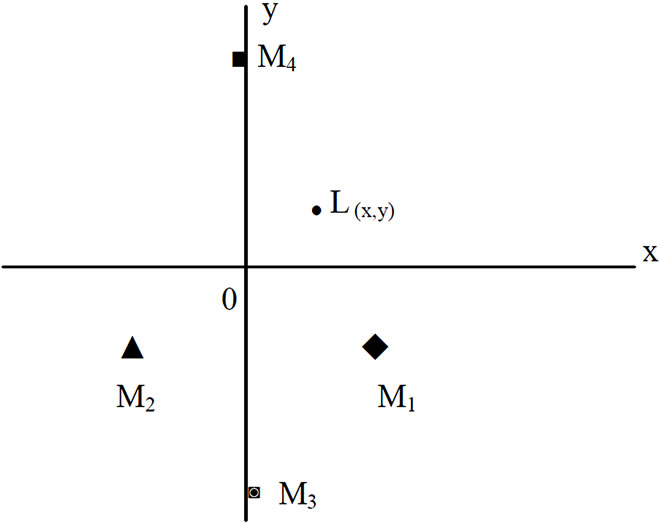
Figure 1. Factory’s location in large geographical area.
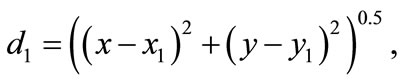 (3a)
(3a)
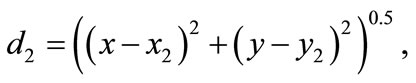 (3b)
(3b)
 (3c)
(3c)
The distance between the factory L and the market M4 is given by d4:
 (3d)
(3d)
If the amount of the material m3 is equal to QS and the fixed cost is F, the firm’s profits YM is given by equation (4),
 (4)
(4)
Making use of the law of equi-marginal productivity, that is, the ratio between the productivities of the two materials should be equal to the ratio between the delivered prices of them, quantities of the materials are derived as equations (5a) and (5b): (For simplicity, α and β are assumed α = β = 0.4):
 (5a)
(5a)
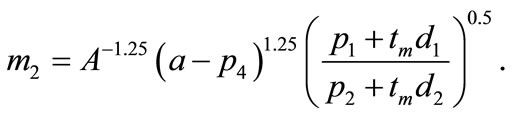 (5b)
(5b)
Since quantity of the material m3 is assumed to be a linear function of amount of the final goods, it is simply given by (5c),
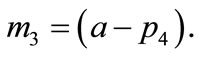 (5c)
(5c)
From the above equations, the firm’s cost C is obtained,
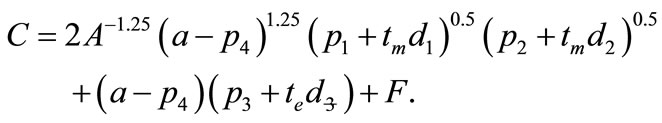 (6)
(6)
Thus, the firm’s profit function is rewritten as equation (7):
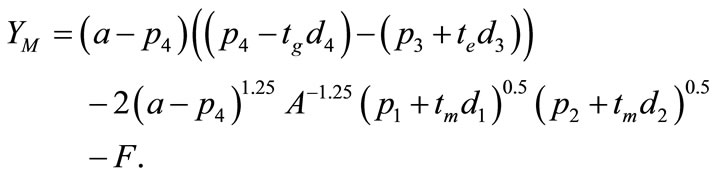 (7)
(7)
2.2. Determination of the Factory’s Location and Price of the Final Good
From the equation (7) it is possible to derive the profitmaximizing location (X, Y) and the price p4. A method to obtain them is to use a usual numerical calculation. In this case, however, the gradient dynamics which is shown by Puu (1998) is appropriate method since the possibility to derive the solution becomes higher by using this one. The essence of this method is that first, an initial value set is given to xn, yn, and p4n in the following equations (8a, b, c) as a temporal solution, and obtain the values of xn+1, yn+1, and p4n+1 by calculations indicated by the three Equations (8a), (8b), (8c). And then, the same calculation is iterated until a given tentative solution can be approximately judged as the solution: When the values of (xn+1, yn+1, p4n+1) in Equations (8a), (8b), (8c) become approximately the same as those of (xn, yn, p4n), this value set can be admitted as the solution.
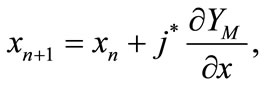 (8a)
(8a)
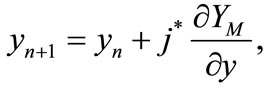 (8b)
(8b)
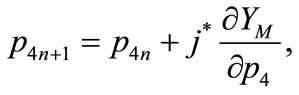 (8c)
(8c)
where j is the width of a step and n shows the number of the calculation, and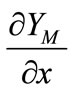 ,
, 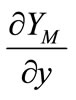 , and
, and 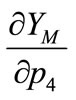 are given by Equations (9a), (9b), and (9c),
are given by Equations (9a), (9b), and (9c),
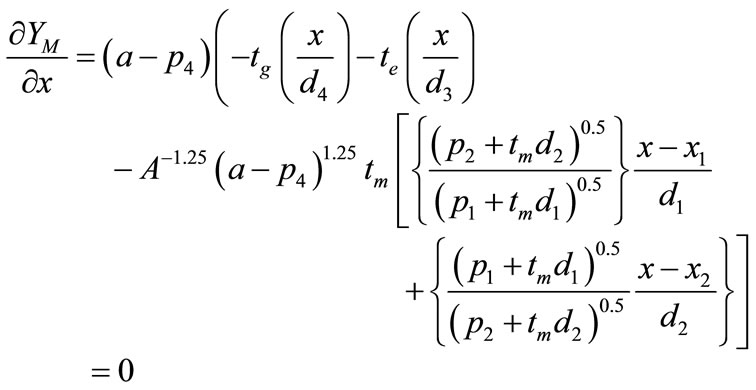 (9a)
(9a)
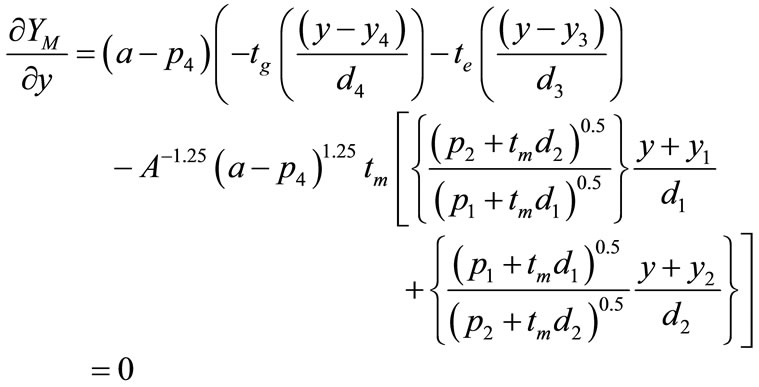 (9b)
(9b)
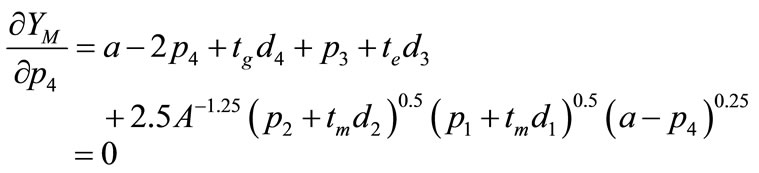 (9c)
(9c)
For example, assigning following values to the parameters, (x1 = 3, y1 = –0.5), (x2 = –1.73, y2 = –0.5), (x3 = 0, y3 = –1.5), (x4 = 0, y4 = 1), p1 = 2, p2 = 0.1, p3 = 0.2, tm = 0.11, te = 0.01, tg = 0.225, a = 5.5, A = 1, F = 0, the optimal location and price is obtained by this method as, (X = 1.732, Y = –0.5, P4 = 3.85)4.
Figure 2 shows a route from the first tentative solution to the final solution. In this case, the amount of production QS = 1.65, the materials m1 = 0.372, m2 = 9.359, and the profits of the firm YM is 3.564.
Now, it is not always possible to identify directly the profit-maximizing location (X, Y) and the price P4 because chaotic phenomenon often emerges in the process to reach the solution. When chaotic phenomenon appears, the solution is hidden by the phenomenon. Thus, this case becomes troublesome to obtain the solution. Let us concretely drive a chaotic phenomenon by the gradient dynamics, changing the parameter of A, which shows the productivity of the factory, from 1 to 2.62, and te = 0.105, p3 = 0.1, chaotic phenomenon appears near the market. Figure 3 shows this chaotic phenomenon.

Figure 2. A path to the solution.
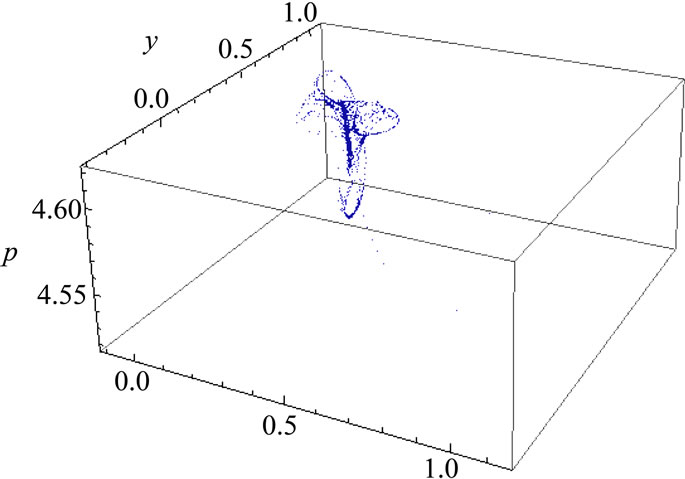
Figure 3. A chaotic phenomenon in the area near the market place M4.
It may suggest that an increase of the productivity of the factory leads the factory toward the market.
When a chaotic phenomenon emerges in the calculation process, additional calculation is needed to obtain the solution; it is necessary in this case to derive the firm’s profits at many points in the range of the phenomenon and to compare the obtained profits in order to specify approximately the optimal location site and price of the finished goods. Although this chaotic phenomenon seems to be troublesome for the firms that search the best location point, the phenomenon may provide useful information to the firms. The next subsection explains the usefulness of these chaotic phenomena.
2.3. Usefulness of Chaotic Phenomena in the Firm’s Location Selection
Chaotic phenomenon shown in the figure can be interpreted from the economic viewpoint as follow: If the firm decides the location site of the factory and price of the goods in the sphere of the chaotic phenomenon, the firm’s profits may not so decrease from the maximum level because the optimal location and price are contained in this sphere. It can be, therefore, considered that the range where the phenomenon occurs indicates a kind of a prospective region for a possible factory’s location. Thus, the manufacturing firm can squeeze the searching area in a large geographical space; they can reduce significantly the inquiring costs. Chaotic phenomena may provide manufacturers with useful information of possible location sites when the firms do not have adequate information about many sites in a large space.
It is also considered that even if the firm could identify the optimal site for the factory, it might not establish a factory at that place by some reasons. For instance, the place has been occupied by another firm, or land price is too expensive. In these cases, the firm has to search the second best sites around the optimal place. In this searching, chaotic phenomenon can be used for squeezing the spatial range to be searched: The firm can easily find out the second best sites around the best point in a relatively short period. Chaotic phenomena could be useful for alleviating the firms’ location problems.
3. The Central Place System as a Location Factor
If the prospective region is completed, a firm sets about selecting a potential area for a factory’s location within this region. In this selection of area, the firm can consider location issue in a broader perspective: Since within this region the firm’s profits are not so different, besides profits level, other location factors including workers’ welfare can be incorporated into the firm’s location decision. This paper proposes that the central place system is able to play an important role in a firm’s selecting of a potential area within the prospective region5.
3.1. The Central Place System Supporting Laborers and Firms
Laborers turn into consumers after they leave factories. They need various sorts of goods to sustain their lives. All goods are not supplied by a single retailer, but they are provided by many retailers scattering in area. Each retailer participates to location system with many retailers: This participation increases quantity purchased and retailer’s profits due to the reduction of transport costs borne by consumers. Location system of the retailers is called the central place system. It can be said that since the central place system sustains laborers’ lives, this system is indispensable for factory’s location.
In a region there are many central place systems which have different economic performances. Difference of their performances attracts the attention of the firms which plan to construct factories. Hence, structure of the central place system is considered as an important location factor for manufacturers.
The studies of the central place systems have been compiled on the memorable works of Christaller and Lösch. Reviewing a literature of the systems from the viewpoint of economics shows that Christaller’s theory is founded in quasi-monopolistic economic situation, while Lösch’s is formed on the monopolistic competition6. This paper, using Christaller’s work, builds two central place systems and inquires their economic performances. The performances are measured in terms of total quantity demanded and total profits of retailers. The revealing the difference in the performances makes it clear why the manufacturers should pay their attention to the structure of the systems that lay on a region.
3.2. Spatial Structures of Two Central Place Systems
Two central place systems which have different spatial structure are introduced to examine how the structures affect economic performances of the systems: One system is constructed by the supply principle; another is constructed by the transport principle.
Figure 4(a) shows the central place system formed by the supply principle. Point L forms the largest central place. This place sells four kinds of goods which are sold individually in four markets with different sizes according to the character of goods. Of four markets the largest market is shown by the bold lines. Points M1-M6, which carry three kinds of goods, are settled at the six vertices of the largest market; they are medium central places. Biggest markets of them are shown by the thin lines. Points S1-S6, which sell two kinds of goods, locate at the six vertices of market areas of the medium central places. They are small central places. Smallest central places H, which are not shown in Figure 4(a), sell one kind of goods.
Figure 4(b) describes the central place system formed by the transport principle. Point L is the largest central place. Location and market of this place are the same as those of the supply system. Medium central places, however, are settled at the mid-points of the six sides of the largest market. These central places are shown by points M1-M6. As a result, both their location and market pattern are different those of the supply system. This market formation is shown by the thin lines. Smaller central places S and H are also sited at the mid-points of the sides of the market areas of the higher-order central places. Points Si (i = 1, 2, ···, 8) show small central places, their location and market size are also different from those of the supply system.
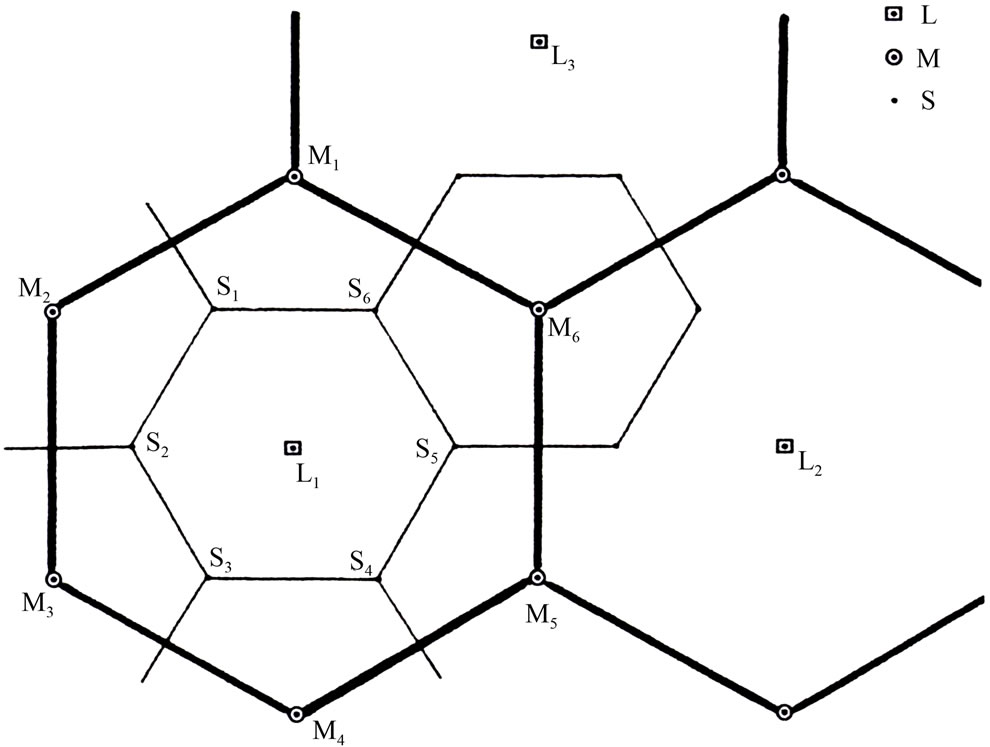 (a)
(a)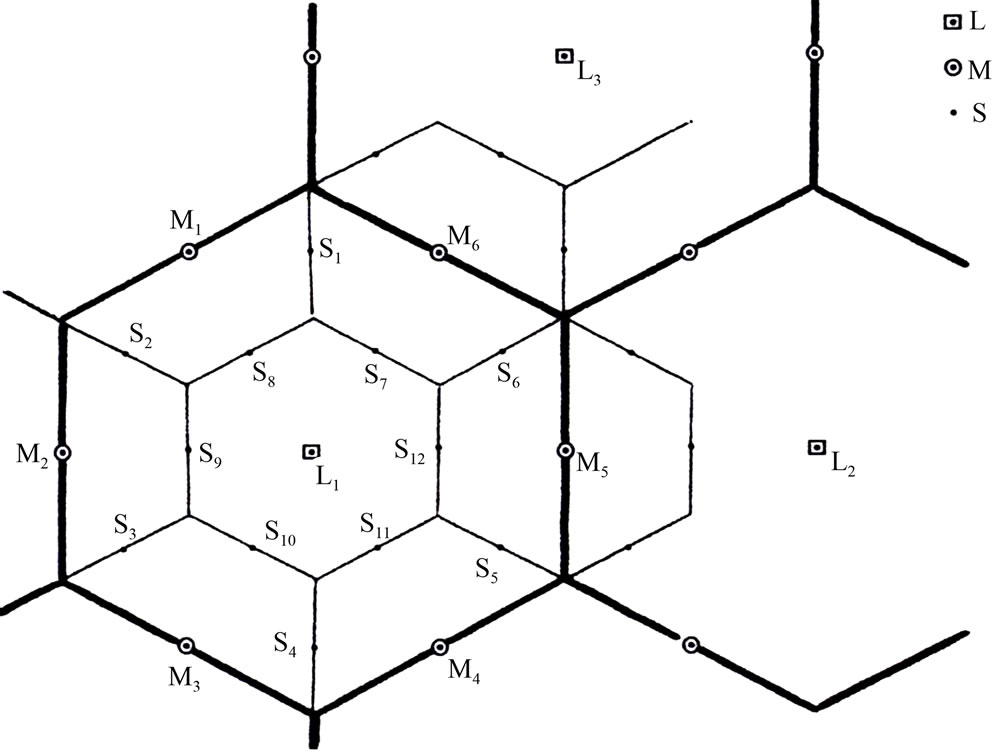 (b)
(b)
Figure 4. (a) Central place system formed by the supply principle; (b) Central place system formed by the transportation principle.
3.3. Economic Performances Achieved in the Central Place System
3.3.1. Basic Assumptions
Quantity demanded and retailers’ profits achieved in the central place system are derived under following assumptions7.
1) Consumers live evenly in area. They have the same demand function:
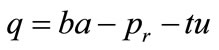 (10)
(10)
where q is quantity demanded, a is the maximum reservation price, b is the coefficient attached to a. According to the b’s value, the kind of good is specified. pr is price of the good at retailer’s shop. t is the transportation cost per mile, u is distance from a consumer to a retailer.
2) All consumers are supplied with all kinds of goods. The profits of the retailers dealing with the same sort of good are equal. Therefore, the retailers carrying with the same kind of good have the same market in size and shape: The possible market shapes are limited to three shapes, triangle, square, and hexagon. This paper adopts hexagonal market area. Quantity demanded in a market area, Qr, is derived by equation (11).
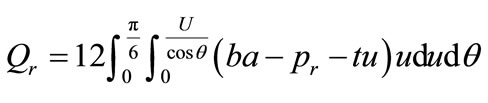 (11)
(11)
where U is the radius of the inscribed circle of market in question. θ is an angle formed at the firm’s location by two lines, one is the line connecting the firm’s location and the mid-point of the side of the market; the other is the line connecting the firm’s location and a vertex of the market. The value of θ is 30˚.
3) Retailer’s cost function is given by equation (12),
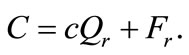 (12)
(12)
where C is total cost, c and Fr are marginal cost and fixed cost, respectively. Profit of a retailer Yr, therefore, is given by equation (13),
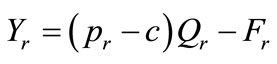 (13)
(13)
4) Retailer sets price to maximize its profit. The optimal price is derived from equation (13). Optimal price is given by equation (14),
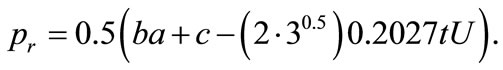 (14)
(14)
3.3.2. Performance of the Central Place System by the Supply Principle
If the radius of the largest market is given UL = 0.6495a, the radiuses of markets of other central places M, S, and H are uniquely settled as UM = 0.375a, US = 0.2165a, and UH = 0.125a. By these radiuses the b’s value in equation (10) is limited into the range from 1.5 to 0.19: Furthermore, the allocation of the b’s values between central places, L, M, S, and H are determined: Table 1 shows the kinds of goods sold by central places of each level by using b’s value.
Subsequently, assume that transport cost per mile t is 1, marginal cost c is zero. And fixed costs Fr of retailers in each level are assumed as follows: fixed cost of the retailers which have the largest market is 0.001a4; that of retailers whose market are medium and locate at places M is 0.00005a4; similarly, 0.00001a4 is assigned to the retailers at S, 0.000005a4 is allocated to the retailers at smallest places H.
Let us derive total quantity demanded TQ and total profit of all retailers TYr in this system. First, sales amounts Qt of the goods indicated by the b’s values of 1.5 - 1 are derived by equation (15):
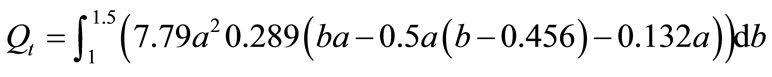 (15)
(15)
Qt is 0.2900a3. Profits of the retailers are as Equation (16).
 (16)
(16)
Secondly, the retailers which locate at both the largest place and medium ones sell the goods whose b values belong in the range from 1 to 0.58. Sale amounts of these goods are obtained8 Qt = 0.1617a3. And profits of these retailers are Yrt = 0.0448a4. Similarly, quantities demanded in smaller markets and profits of the retailers at the lower central places can be obtained. They are shown by Qt and Yrt in Table 1. Using these figures in this Table, total quantity of all kinds of goods, TQ and total profit of
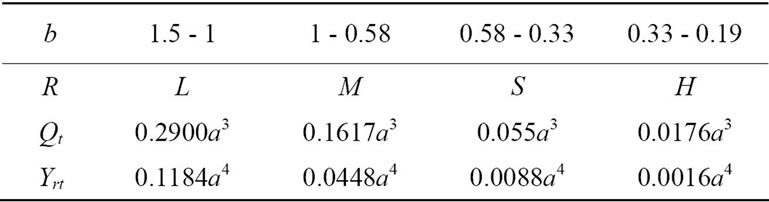
Table 1. Performance of the central place system of the supply principle.
all retailers, TYr are derived as TQ = 0.5246a3 and TYr = 0.1736a4.
3.3.3. Performance of the System of the Transport Principle
The radius of the largest market is also assumed UL = 0.6495a in the system formed by transportation principle. Then, both location and market of the largest central place are the same as the previous system. While location and market pattern of central places M, S, and H are different from those of the supply principle. The radiuses of their markets become smaller; UM = 0.3248a, US = 0.1624a, and UH = 0.0812a. Corresponding to the reduced market sizes, in this system the lower bound of b’s value is extended to 0.125, and the allocation of b’s values between central place levels is not coincided with that of the supply. The b’s values allocation is shown in Table 2. Sales amounts and retailer’s profits in each level are obtained by the same method used in the above section. They are shown by Qt and Yrt in Table 2. Total quantity demanded and profit in the system are derived as TQ = 0.5377a3, TYr = 0.1794a4, respectively.
3.3.4. A Manufacturing Firm’s Selection of the System
Tables represent the differences in economic performances achieved by the two systems. Performances in the system formed by the transport principle are larger than that of the supply principle. The system of the transportation principle is superior to the system of the supply one. It should be also noticed, however, that demanded quantities and retailers’ profits achieved at the central places of S and H level in the system of the supply principle are greater than those of the transport principle.
Which central place system is preferred by a manufacturing firm depends on the firm’s interest. If the firm attaches importance to laborers’ welfare, it selects the system of the transport principle because it provides consumers with larger quantity of goods. Furthermore, since this system produces more retailers’ profits, tax revenue may be relatively higher, and then public investment in infrastructure is larger, which leads to encourage firm’s activity and improve workers’ welfare in a region. Therefore, the system of the transport principle attracts the firm’s attention. While, if the firm makes much of demanded quantities of goods and profits of the retailers in relatively smaller central places, it selects the system of the supply principle, because small central places in this
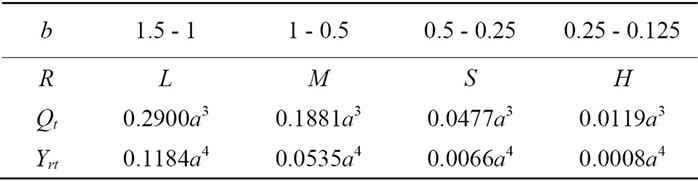
Table 2. Performance of the system of the transport principle.
system achieve greater quantity of goods and the retailers’ profits. It is said that the central place systems are important location factor in a firm’s selecting an area within the prospective region.
4. Firm’s Decision-Making of Location
Based on the previous analysis, it is considered that a firm takes four steps to determine its factory’s location in a large geographical area.
1) Based on the fundamental information of materials’ prices, their producing places and market condition, the firm decides the spatial range in which the factory should be located. Chaotic phenomenon has an opportunity to be used to the definition of the range, prospective region, in a large space.
2) Within this region the firm selects a potential area. Because the structure of central place system in the area influences not only the firm’s profits but workers’ welfare, this system can play an important role in the selecting area.
3) An urban district in the system is chosen by the firm. Since individual urban districts have different economic characteristics, each district in the system has the possibility to attract a factory: For example, the largest city provides various kinds of economic functions and is equipped with large scale infrastructures. Thus, this city may be chosen by the factories that need various external agents with respect to finance, market information and recruitment and so on. While, if a factory requires a large plot to produce goods, it may select a small city.
4) Finally, the firm decides a site within the urban district. The firm estimates various practical factors about potential sites in question such as the price of land, surrounding environment, and the difficulty of negotiation with landlords.
These steps should be taken by many manufacturing firms when they research a site for a factory within a large geographical area.
5. Conclusion Remarks
Location of factories affects various economic activities of a firm in different ways: It influences the production mode, the logistics of intermediate goods and final ones, and the price of goods and so on. Location issue has been one of the important tasks for manufacturers. Nowadays, there are two trends which characterize the manufacturing firms’ location choices: First, manufacturers search the most preferable site within vast geographical area: Secondly, many hi-skilled workers reside at the place that possesses comfortable circumstances to live. Without consideration of these facts current firms would not successfully manage its factories.
Corresponding to this view, the paper proposes that a firm should take a series of steps to determine a factory’s location site; 1) determination of a prospective region; 2) selection of a potential area within the region; 3) choice of an urban district within the area; 4) decision of a site in the district. In the first step, chaotic phenomenon may have the possibility to be used to define a prospective range. In the second step, a firm should consider the central place system as a factor to select an area. Because the central place system directly influences workers’ lives and indirectly affects firm’s profit, this system plays a significant role in a firm’s area selections.
Both fragmentation of production processes proceeds on a world wide scale, and fragmented production blocs are now able to move in the long distance and they across the borders of countries. At the same time, there are many regions which need many factories to vitalize their economies. Considering the results derived from the above analysis, it may be said that the local government of a region are required to not only care individual cities, but also to restructure the existing urban systems in order to attract factories into the region. The urban system should be considered as an important location factor to attract firms’ location and to develop regional economy.
REFERENCES
- S. W. Arndt and H. Kierzkowski (Eds.), “Fragmentation,” Oxford University Press, Oxford, 2001.
- B. Dluhosch, “Industrial Location and Economic Integration-Centrifugal and Centripetal Forces in the New Europe,” Edgar Elgar, Cheltenham, 2000.
- W. Christaller, “Die Zentralen Orte in Süddeutschland,” G. Fischer, Jena, 1933.
- A. Lösch, “Die räumliche Ordnung der Wirtshaft,” G. Fischer, Stuttgart, 1940.
- T. Ishikawa, “Determination of a Factory’s Location in a Large Geographical Area by Using Chaotic Phenomena and Retailers’ Location Networks,” Timisoara Journal of Economics, Vol. 3, 2009, pp. 141-150.
- T. Puu, “Gradient Dynamics in Weberian Location Theory,” In: M. J. Beckmann, et al., Eds., Knowledge and Networks in a Dynamic Economy, Springer, Vol. 34, 1998, pp. 221-233.
- R. Capello, “Regional Economics,” Routledge, London, 2007, pp. 203-205.
- T. Ishikawa and M. Toda, “Some Econ Economic Extensions of Central-Place Theory Involving Profit Maximisation,” Urban Studies, Vol. 37, No. 3, 2000, pp. 481-495. doi:10.1080/0042098002078
NOTES
1Fragmentation of production processes has been examined by many scholars; see Arndt Kierzkowski [1].
2Fragmentation derived from cost completion is explained in detail by Dluhosch [2].
3The possibility that chaotic phenomena are used in the firm’s decision-making is firstly pointed out by Ishikawa [5] based on the works of Puu [6] and the role of retailers’ networks in the firm’s decisionmaking is also analyzed by his paper.
4The values for the parameters are selected to be solved easily by a usual numerical calculation method.
5Capello [7] stresses the importance of the role of urban system in firm’s location choices in the context of local development.
6The relationship between competition types in market and central place systems is examined by Ishikawa-Toda [8].
7Social surplus could be used as a measure of economic performance.
8By using the way shown by equation (15), sale amounts of goods which are sold in a market of medium central place are obtained as 0.0539a3. Since the number of this market in this system is three, sum of quantities purchased is calculated as 0.1617a3. And then, profits of all retailers dealing with these goods are derived as 0.0448a3.

