Vol.2, No.5, 476-483 (2010) Natural Science
http://dx.doi.org/10.4236/ns.2010.25059
Evidence for the existence of localized plastic flow
auto-waves generated in deforming metals
Lev B. Zuev*, Svetlana A. Barannikova
1Institute of Strength Physics and Materials Science, Siberian Branch of Russian Academy of Sciences, Tomsk, Russia;
[e-mail]; *Corresponding Author:
Received 12 January 2009; revised 26 February 2009; accepted 8 March 2009.
ABSTRACT
The localized plastic flow auto-waves observed
for the stages of easy glide and linear work
hardening in a number of metals are considered.
The propagation rates were determined expe-
rimentally for the auto-waves in question with
the aid of focused-image holography. The dis-
persion relation of quadratic form derived for
localized plastic flow auto-waves and the de-
pendencies of phase and group rates on wave
number are discussed. A detailed comparison of
the quantitative characteristics of phase and
group waves has revealed that the two types of
wave are closely related. An invariant is intro-
duced for localized plastic flow phenomena
occurring on the micro-and macro-scale levels
in the deforming solid.
Keywords: Metallic Materials; Mechanical Testing;
Optical Interferometry; Strengthening and
Mechanisms; Crystal Plasticity; Fracture
1. INTRODUCTION
The experimental evidence obtained previously [1-4]
suggests that the plastic deformation tends to localize in
the deforming solid over the entire flow process. Plastic
flow localization is most pronounced on the macro-scale
level where the type of local strain pattern is governed
by the law of work hardening acting at a given flow stage,
i.e.

  ddE 1 (here Е is the elasticity
modulus). The localization of plastic deformation will
assume in this case the form of auto-wave1, i.e. a
self-excited process [3,4]. The occurrence of auto-
wave processes by the plastic deformation is consi-
dered, e.g. in the context of gradient plasticity theory
[6-8].
A considerable body of experimental and theoretical
evidence pertaining to plastic flow macro-localization
has been obtained thus far [1-4,6], which suggests that
the macro-scale inhomogeneities of localized plastic
flow have a typical scale of about 10–2 m. A characteris-
tic picture is created in the deforming specimen where
deformed material zones move in a concerted manner,
generating thereby localized plastic flow auto-waves,
which have typical wavelength of about 10–2 m. Thus a
deforming body would spontaneously separate into al-
ternating deformed and undeformed zones (Figure 1).
Following H. Hacken [9], the spontaneous emergence of
plastic flow inhomogeneities might be regarded as a
manifestation of self-organization processes occurring in
the deforming medium.
2. EXPERIMENTAL PROCEDURE AND
MATERIALS TESTED
On the base of available experimental evidence [1-4],
the quantitative characteristics of auto-wave processes
were determined for a wide circle of pure metals and
alloys, both single crystals and polycrystalline ones,
having FCC, BCC and HCP crystal lattice. It is found
that the mechanical characteristics of investigated mate-
rials and the shape of plastic flow curves obtained for the
test specimens would vary significantly, depending on
chemical composition, grain size of polycrystalline ma-
terials and extension axis orientation of single crystals.
In what follows the distinctive features common to all
the investigated materials are discussed.
The experimental observations of localized plastic
flow auto-waves [1-4] were conducted using the tech-
nique of focused-image holography related to speckle
photography [10]. This technique was specially deve-
1Autowaves are opposed to, e.g. elastic waves of the type
 kxwt sin , in that they are solutions to parabolic differential
equations in the partial derivatives
 yDyxy


 ,

[5], while
the latter obey hyperbolic equations of the type ycy 
 2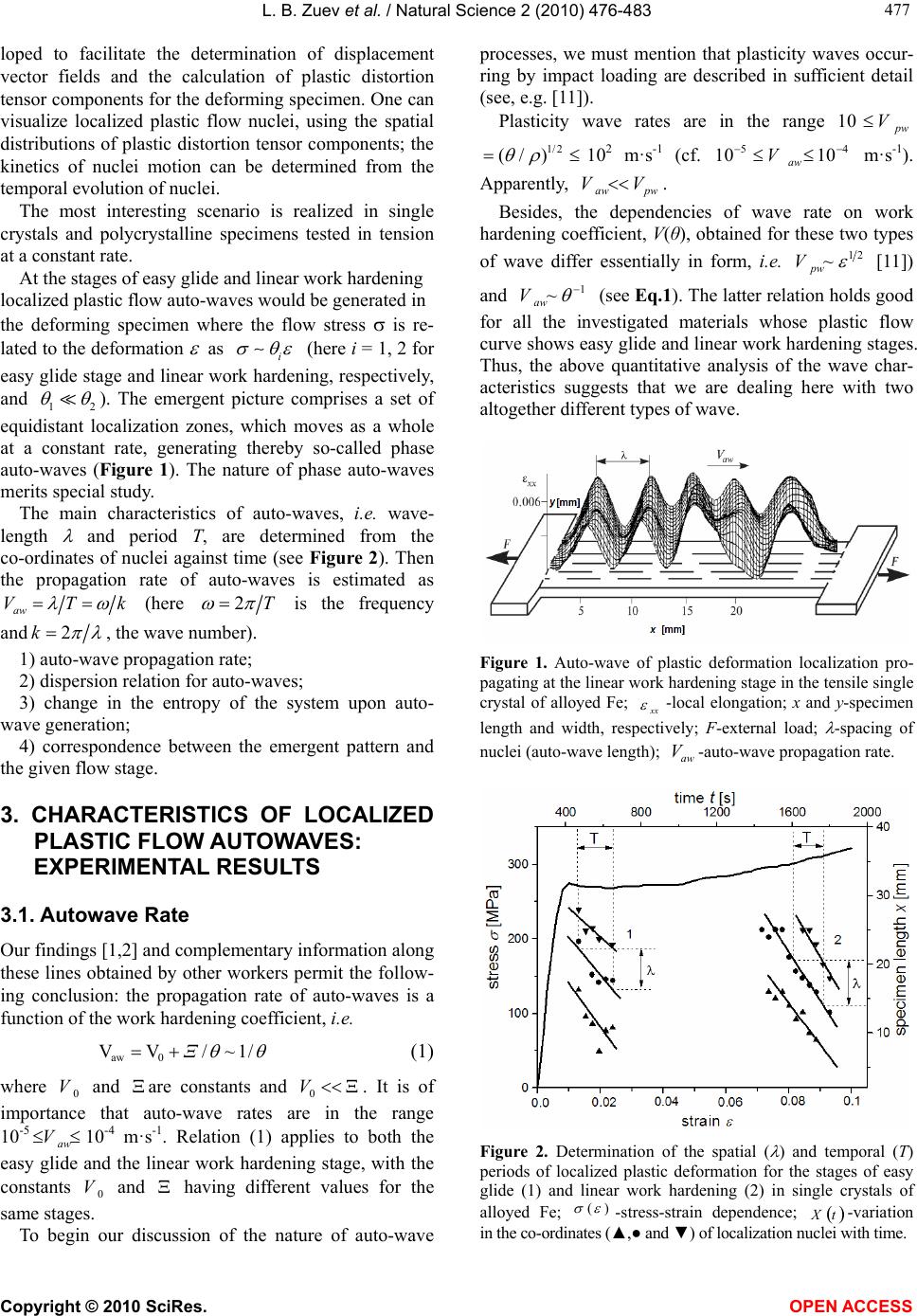
 .

L. B. Zuev et al. / Natural Science 2 (2010) 476-483
477
477
loped to facilitate the determination of displacement
vector fields and the calculation of plastic distortion
tensor components for the deforming specimen. One can
visualize localized plastic flow nuclei, using the spatial
distributions of plastic distortion tensor components; the
kinetics of nuclei motion can be determined from the
temporal evolution of nuclei.
The most interesting scenario is realized in single
crystals and polycrystalline specimens tested in tension
at a constant rate.
At the stages of easy glide and linear work hardening
localized plastic flow auto-waves would be generated in
the deforming specimen where the flow stress  is re-
lated to the deformation  as i

  (here i = 1, 2 for
easy glide stage and linear work hardening, respectively,
and 12

 ). The emergent picture comprises a set of
equidistant localization zones, which moves as a whole
at a constant rate, generating thereby so-called phase
auto-waves (Figure 1). The nature of phase auto-waves
merits special study.
The main characteristics of auto-waves, i.e. wave-
length
 and period Т, are determined from the
co-ordinates of nuclei against time (see Figure 2). Then
the propagation rate of auto-waves is estimated as
kTVaw


 (here T


2 is the frequency
and


2k, the wave number).
1) auto-wave propagation rate;
2) dispersion relation for auto-waves;
3) change in the entropy of the system upon auto-
wave generation;
4) correspondence between the emergent pattern and
the given flow stage.
3. CHARACTERISTICS OF LOCALIZED
PLASTIC FLOW AUTOWAVES:
EXPERIMENTAL RESULTS
3.1. Autowave Rate
Our findings [1,2] and complementary information along
these lines obtained by other workers permit the follow-
ing conclusion: the propagation rate of auto-waves is a
function of the work hardening coefficient, i.e.


 /1~/VV 0aw  (1)
where 0 V and are constants and 
0
V. It is of
importance that auto-wave rates are in the range
10-5 aw V10-4 m·s-1. Relation (1) applies to both the
easy glide and the linear work hardening stage, with the
constants 0 V and  having different values for the
same stages.
To begin our discussion of the nature of auto-wave
processes, we must mention that plasticity waves occur-
ring by impact loading are described in sufficient detail
(see, e.g. [11]).
Plasticity wave rates are in the range 10
p
w
V

1/2
(/ ) 

102 m·s-1 (cf. 54 10 10
aw
V

 m·s-1).
Apparently, pwaw VV

.
Besides, the dependencies of wave rate on work
hardening coefficient, V(θ), obtained for these two types
of wave differ essentially in form, i.e. 21 ~ 
pw
V [11])
and 1 ~ 
aw
V (see Eq.1). The latter relation holds good
for all the investigated materials whose plastic flow
curve shows easy glide and linear work hardening stages.
Thus, the above quantitative analysis of the wave char-
acteristics suggests that we are dealing here with two
altogether different types of wave.
Figure 1. Auto-wave of plastic deformation localization pro-
pagating at the linear work hardening stage in the tensile single
crystal of alloyed Fe; xx

-local elongation; x and y-specimen
length and width, respectively; F-external load;  -spacing of
nuclei (auto-wave length); aw V-auto-wave propagation rate.
Figure 2. Determination of the spatial (  ) and temporal (T)
periods of localized plastic deformation for the stages of easy
glide (1) and linear work hardening (2) in single crystals of
alloyed Fe; )(


-stress-strain dependence;


tX -variation
in the co-ordinates (▲,● and ▼) of localization nuclei with time.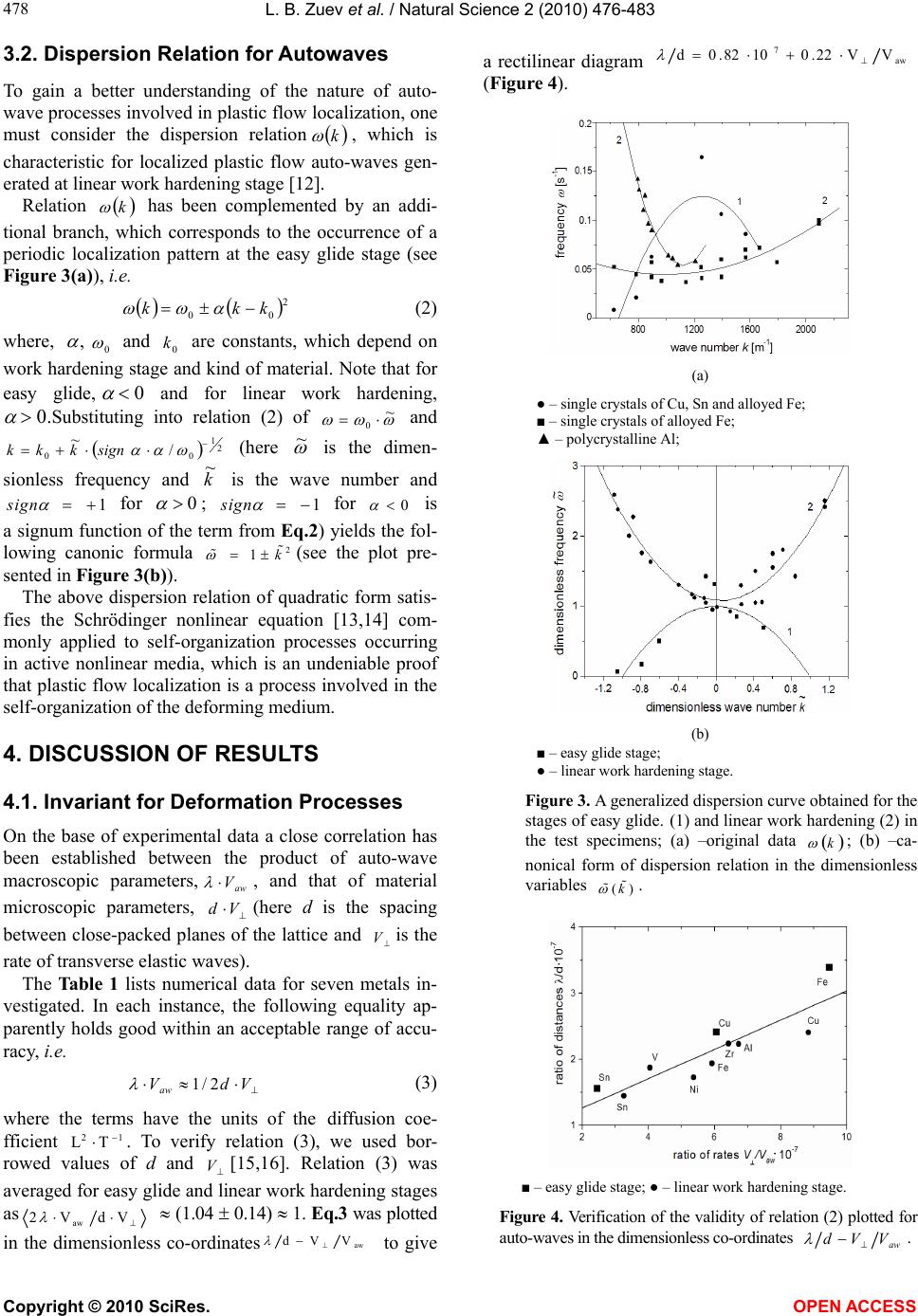

L. B. Zuev et al. / Natural Science 2 (2010) 476-483
478
3.2. Dispersion Relation for Autowaves
To gain a better understanding of the nature of auto-
wave processes involved in plastic flow localization, one
must consider the dispersion relation  k

, which is
characteristic for localized plastic flow auto-waves gen-
erated at linear work hardening stage [12].
Relation  k 
has been complemented by an addi-
tional branch, which corresponds to the occurrence of a
periodic localization pattern at the easy glide stage (see
Figure 3(a)), i.e.
 
2
00 kkk 

(2)
where, ,

0

and 0 k are constants, which depend on
work hardening stage and kind of material. Note that for
easy glide,   and for linear work hardening,
 Substituting into relation (2) of



~
0

 and

2
1
00 /
~

  signkkk (here

~
is the dimen-
sionless frequency and k
~
is the wave number and
1sign

 for 0

; 1sign

 for 0


is
a signum function of the term from Eq.2) yields the fol-
lowing canonic formula 2
1k 


(see the plot pre-
sented in Figure 3(b)).
The above dispersion relation of quadratic form satis-
fies the Schrödinger nonlinear equation [13,14] com-
monly applied to self-organization processes occurring
in active nonlinear media, which is an undeniable proof
that plastic flow localization is a process involved in the
self-organization of the deforming medium.
4. DISCUSSION OF RESULTS
4.1. Invariant for Deformation Processes
On the base of experimental data a close correlation has
been established between the product of auto-wave
macroscopic parameters,aw
V

, and that of material
microscopic parameters,  Vd (here d is the spacing
between close-packed planes of the lattice and 
Vis the
rate of transverse elastic waves).
The Table 1 lists numerical data for seven metals in-
vestigated. In each instance, the following equality ap-
parently holds good within an acceptable range of accu-
racy, i.e.


 VdVaw 2/1

(3)
where the terms have the units of the diffusion coe-
fficient 12 TL  . To verify relation (3), we used bor-
rowed values of d and 
V[15,16]. Relation (3) was
averaged for easy glide and linear work hardening stages
as 
VdV2 aw 
 (1.04  0.14)  1. Eq.3 was plotted
in the dimensionless co-ordinatesaw
VVd  
to give
a rectilinear diagram aw
7VV22.01082.0d
 
(Figure 4).
(a)
● – single crystals of Cu, Sn and alloyed Fe;
■ – single crystals of alloyed Fe;
▲ – polycrystalline Al;
(b)
■ – easy glide stage;
● – linear work hardening stage.
Figure 3. A generalized dispersion curve obtained for the
stages of easy glide. (1) and linear work hardening (2) in
the test specimens; (a) –original data
 k

; (b) –ca-
nonical form of dispersion relation in the dimensionless
variables ()k


.
■ – easy glide stage; ● – linear work hardening stage.
Figure 4. Verification of the validity of relation (2) plotted for
auto-waves in the dimensionless co-ordinates aw
VVd 


.

L. B. Zuev et al. / Natural Science 2 (2010) 476-483
479
479
Table 1. The productsaw V

and 
Vd matched for easy glide and linear work hardening stages.
Flow stage Metal aw
V

 107 (m2/s) D  1010 (m) 
V  10–3 (m/s)

Vd  107 (m2/s) 


Vd
Vaw
 2
Cu 1.90 2.08 2.30 4.78 0.79
Fe 3.03 2.07 3.32 6.87 0.88
Easy glide Sn 3.28 2.91 1.79 5.20 1.26
Cu 3.60 2.08 2.30 4.78 1.50
Al 7.92 2.33 3.23 7.52 2.10
Zr 1.92 2.46 2.25 5.53 0.70
V 2.80 2.14 2.83 6.06 0.92
Fe 2.55 2.07 3.32 6.87 0.74
Ni 2.10 2.03 3.22 6.54 0.64
Linear work
harde-ning
Sn 2.34 2.91 1.79 5.20 0.90
Eq.3 relates the micro-scale characteristics d and
V,
which are observed for elastic waves propa-gating in
crystals, to the macro-scale parameters

and aw
V,
which are observed for elastic waves propagating in
crystals, to the macro-scale parameters

and aw
V,
which are obtained for localized plastic flow auto-waves
generated in the same crystals. The products of these
values,  Vd and aw
V 
, are invariants for elastic and
plastic deformation processes, respectively (<< 1 and  1,
respectively). The above regularity stems from the fact
that the processes of elastic and plastic deformation are
closely related. In the course of deformation the
redistribution of elastic stresses occurs via micro-scale
processes at the rate 
V, while the rearrangement of
localized plastic flow nuclei involves macro-scale
processes occurring at the rate aw V, with the processes
of both types being related by Eq.3. Thus, the macro-
localization phenomena must be regarded as an attribute
of plastic deformation rather than a random disturbance
of plastic flow homogeneity.
4.2. On the Physical Meaning of Relation (1)
By considering the nature of localized plastic flow
auto-waves, it might be pertinent to discuss the origin of
dependency 1
~ 
aw
Vand, in particular, the meaning of
deformation processes occurring in crystals is the
propagation rate of elastic waves, i.e. sound rate S V.
For most metals S
V  5103 m·s-1; hence 10
10
S
V.
To account for relation (1), the Dirac large-numbers
hypothesis [17] was invoked. An appropriate dimen-
sionless relation of the same order was also required
which could be applied to the quantities associated with
the deformation processes2. The relation of deforming
medium’s viscosities defined for two limiting cases was
thought to be an appropriate one, with the limiting cases
being the quasi-viscous motion of dislocations, invol-
ving no interaction with local obstacles, and the break-
away of dislocation segments from local obstacles. In
the former case, the motion of dislocations occurs at
high acting stresses; the dislocation velocity as a func-
tion of applied stress  has the form BbVdisl   (here
b is the Bürgers vector; B  (1-3)10–4 Pas is the coeffi-
cient of dislocation drag, which characterizes the viscos-
ity of phonon gas in the crystal) [18]. In the latter case,
viscosity is defined from internal friction measurements
to yield   3106 Pas [19]. In the case of ultrasound
waves, stresses have low amplitudes; therefore, the vis-
cosities observed for micro-scale plastic deformation
processes might have similar values. Hence the ratio

B

1010 and, consequently, BVS  . Then one
can write
S
V/B



(4)
Eq.4 can be interpreted as follows. Complex systems
capable of structure formation will spontaneously sepa-
rate into an information subsystem and a dynamic one
[20]. It is thus assumed that the information subsystem,
which is characterized by low-amplitude stresses and
high viscosity, is represented by acoustic emission sig-
nals whereas the dynamic subsystem, which is charac-
terized by high-amplitude stresses and low viscosity, is
represented by the motion of individual dislocations and
dislocation ensembles, with Eq.4 formalizing the rela-
tionship between the two subsystems. Thus, the former
subsystem is related to the processes involving elastic
wave propagation and the latter, to dislocation plasticity
proper.
To better understand the physical meaning of Eq.1,
one can also invoke the notions incorporated into
the concept of work hardening. It is assumed that




lddVaw ~ (here l is the length of slip line). Accor-
ding to the work hardening concept proposed by Seeger
[21],




*
 l, with and *

depending on ma-
terial kind; for linear work hardening, the coeffi- cient of
work hardening


21
3 nb  (here b is the Bürgers
vector of dislocations and n is the number of dislocations
in a dislocation pileup). In the latter case,2 ~  
, i.e.

L. B. Zuev et al. / Natural Science 2 (2010) 476-483
480
2
aw /d)/(1nbкdV
  (5)
where the coefficient has the units [T–1]. With *  
depending only weakly on material type [21], Eq.1 can
be derived from (5), considering that
 /1)/(  nbкVaw (6)
where )/(
 nbк.
The coefficient  can be calculated by taking into
account that the values and *  depend only weakly on
material kind and deformation [21]. Indeed, the deriva-
tive

ddVaw  1.5·10–2 m·s can be estimated from the
data reported in [1,2]. For the increment in the deforma-
tion

  0.05, an increase in the length of slip line l is
about 3·10–4 m [21]. Hence



/)d/dV(кaw   10
s–1. Provided n  20 [21] and b  2·10–10 m,   8·10–7
m·s-1, which is close to the experimental value


5·10–7 m·s-1.
The physical significance of the above difference lies
in the fact that localized plasticflow auto-waves belong
to an altogether different class of wave phenomena,
which are not identical with plasticity waves [11]. There-
fore, these two types of waves cannot be grouped to-
gether.
4.3. Treatment of Dispersion Relation
Dispersion relation (2) of quadratic form can be ex-
plained as follows. Relation (3) can be rewritten as
kkVdVdVaw  



)4/(/1)2/( (7)
Let the rate of localized plastic flow auto-wave,
graw VV (here Vgr is the group rate); thendkdVaw
 .
Hence
dkkd 


(8)
Integration can be performed for Eq.8 as follows
 
0
00
kk
dkkd 


(9)
to yield the dependence.
  
2
00
2
002kkkkk 
 , which is
identical with dispersion relation (2) derived experi-
mentally for localized plastic flow auto-waves.
Apparently, the dispersion relation of quadratic form
 
2
00kkk 
 , which is obtained for localized
plastic flow auto-waves occurring at the stages of easy
glide and linear work hardening, follows from the equal-
ity 
 VdVaw21  , which relates the macro-scopic
characteristics of localized plastic flow auto-waves and
the microscopic parameters of material crystal lattice.
The right-hand side of Eq.3 can be rewritten as
D
dVd   
2
21 (here D

is the Debye frequency
and D dV



2). Using the well-known formula
DBD k



 (here B k is the Boltzmann constant;

2h

 is the Planck constant and D

is the tempe-
rature-ependent Debye parameter [22]), one can write
/)(2/1 2TkdVVd DBaw    (10)
Eq.10 may be useful since it predicts the temperature
dependence


TV Daw


~ for localized plastic flow
auto-waves [1].
4.4. Group and Phase Rates of Localized
Plastic Flow Autowaves
In accordance with dispersion relation (2), the phase and
group rates of localized plastic flow auto-waves can be
represented in the dimensionless variables

~
and k
~
(see Figures 5(a) and 5(b)) as kkkVph
~
1
~
~
~
~
~
 
and kkddVgr
~
~
~
~
~
 , respectively (see also Figure
3(a)).
From Eq.10 follows that
kkhkdkdV DBDBaw   )/(/1)/( 22  (11)
The experimental evidence suggests that kVgr ~. The
quantity DDBdhkd   22 from (11) is taken to
be a proportionality coefficient, which can be readily
calculated, using d values reported in [15] and the Debye
temperatures,

FeD

420 K and 
AlD

394 K ob-
tained for the single crystals of iron and aluminum [22].
The calculated values of the proportionality coeffi-
cient obtained for the single crystals of iron and alumi-
num are, respectively, hkd DB Fe
2
Fe
  ≈ 3.7·10–7
m2·s–1 and hkd DB Al
2
Al
  ≈ 4.45·10–7 m
2·s–1. The
experimental values determined for the same materials
from the inclination of  kVgr plots are Fe  = (1 ±
0.08)·10–7 m
2·s–1 and Al
 = (12.9 ± 0.15)·10–7 m
2·s–1,
respectively. Matching of the calculated and the experi-
mental values reveals a satisfactory agreement between
the two sets of data.
It also follows from Figures 5(a) and 5(b) that the
functions


kV ph
~
~
and


kVgr
~ ~ show fundamentally
different behaviours for the stages of easy glide and lin-
ear work hardening: in the former case, they would not
intersect for any k
~
values, while in the latter case, they
fully coincide for 1
~
k. The above difference in the
function behaviours is attributable to the fact that the
stage of easy glide is generally characterized by plastic
2We had to overcome a certain difficulty since Dirac’s hypothesis was
initially applied to values in the ratio of about 1032.

L. B. Zuev et al. / Natural Science 2 (2010) 476-483
481
481
flow instabilities, while at the stage of linear work hard-
ening the plastic flow will occur in a steady-state regime,
with the latter case evidently corresponding to the ab-
sence of dispersion, i.e. phgrV
~
V
~
.
4.5. Change in the Entropy of the Deforming
System by Auto-Wave Generation
The dependencies
 
w
V obtained for the above two
types of wave are found to differ radically in form, i.e.
21
~ 
pw
V and
1
~ 
aw
V. It might be also expected that
the thermodynamic properties of the medium, in par-
ticular, entropy, will change in a dissimilar way by the
generation of the two types of wave. It would appear
reasonable to suggest that plastic deformation w
V~


(here w
V is the rate of a certain type of wave). Provided
mobile dislocation density const
m

, the Taylor-
Orowan equation for plastic flow rate dislm Vb
 
 [23]
can be applied to give wdisl VV ~~

. For thermally ac-
tivated dislocation motion, the rate is given as
)/exp(~ TkGV Bdisl  (here ATSUG is the
Gibbs thermodynamic potential; U is the internal energy;
S is the entropy of the process;

 Ais the work of
external stresses by the deformation and  is the activa-
tion volume of an elementary deformation act [23]).
Hence the propagation rate is given for any type of wave
as
)/)(exp()/exp(~~~ TkUkSVV BBdislw





 (12)
The enthalpy

 UH observed for linear work
hardening stage is virtually the same for most metallic
materials. Consequently, taking the logarithm of (12)
evidently yields SV w~ln .
Thus, a close correspondence is found to exist between
the rectilinear diagrams
 
w
V plotted in the co- ordi-
nates

lnln 
w
V for the both types of wave process
(see Figure 6) on the one hand and the linear dependen-
cies

lnS obtained for the same processes on the
other hand. The diagrams were plotted using wave rates
listed in the table for the stage of easy glide in single
crystals and for the stage of linear work hardening in
single crystals and polycrystalline metals and alloys
(Figure 6, lines 1 and 2, respectively). The wave rates
were calculated from the expression 2
1
0)/(
 
p
w
V
(Figure 6, line 3) and the  values, from the loading
curves of investigated materials; besides, borrowed
0

values were used [15].
An analysis of the dependencies


w
V shows that in
the case of plasticity waves, an increase in the entropy of
the system would occur (0S) (see Figure 6, line 3),
which is characteristic for processes accompanied by
dissipation of energy. In the case of auto-waves, the en-
tropy of the system would decrease (0S) (see Figure
6, lines 1 and 2 for easy glide and linear work hardening,
respectively).
The above results suggest that localized plastic flow
waves differ radically from other types of wave process
related to plastic deformation in solids. The generation
of localized plasticity waves would cause a decrease in
the entropy of the deforming system, which is an indica-
tion of its self-organization (ordering) [9] since entropy
is a function of the parameter of order [24]. By consi-
dering localized plastic flow waves, the coefficient of
work hardening 1



might be regarded as a para-
meter of order so that

ln~S. With growing  value,
the entropy of the system would change linearly, with
0


S corresponding to auto-waves and 0S, to
(a)
(b)
Figure 5. Wave number dependencies of phase (■) and
group (●) propagation rates plotted for localized plastic flow
auto-waves in the dimensionless invariables kV
~
~
; (a)
easy glide stage; (b) linear work hardening stage.

L. B. Zuev et al. / Natural Science 2 (2010) 476-483
482
Figure 6. Changes in the entropies of plasticity waves (3)
and of localized plastic flow auto-waves plotted for the
stages of easy glide (1) and linear work hardening (2) in
the co-ordinates

lnln
w
V (see the axis SVw~ln ).
plasticity waves (see Figure 6).
The above suggests that plasticity waves [11] are
commonly known dissipative processes, while localized
plastic flow auto-waves are self-organization processes
that are liable to cause a decrease in the entropy of the
deforming system [9].
4.6. Correspondence Between Localized
Plastic Flow Patterns and Work
Hardening Stages
Of particular importance is the finding that localized
plastic flow patterns emerging in a deforming solid are
related to the respective flow stages [21]. These stages
can be readily distinguished on the flow curve of the
form [21]

n
  0 (13)
where 0

is the proof stress and n is the parabola ex-
ponent. The latter value will change discretely with the
deformation, which enables individual stages to be sin-
gled out on the flow curve.
Using this method, a correspondence rule has been
established for single crystals of metals and alloys and
polycrystalline materials. This holds that
For n = 0 (yield plateau) or n  0 (easy glide), a soli-
tary nucleus of localized plastic flow travels along the
extension axis;
For n = 1 (linear work hardening), localized plastic
flow auto-waves are generated, which have wavelength
and propagation rate aw V;
For n = ½ (parabolic work hardening or Tailor’s stage),
a set of immobile localized plastic flow nuclei is ob-
served;
For 0 < n < ½ (pre-failure stage), collapse of auto-
wave takes place, which corresponds to macro-necking
[25] and
For n = 0, ductile failure of material will occur.
The proposed rule evidently states that typical local-
ization patterns observed on the macro-scale level are
reflections of vastly different microscopic mechanisms
involved in material work hardening at the different flow
stages. This also testifies to the fact that the events in-
volved in the deformation on the micro-scale level are
directly related to those occurring on the macro-scale
level in the deforming medium.
5. CONCLUSIONS
At all its stages the plastic flow involves localization
processes that take the form of different types of auto-
wave. The plastic flow tends to localize over the entire
process; therefore, localization is taken to be its integral
attribute.
The parameters of localized plastic flow evolution are
found to be related to those of elastic deformation proce-
sses as 



VdVaw 2/1

. This suggests that the defor-
mation process will exhibit scale invariance on both the
micro-scale level




Vd and the macro-scale one


aw
V


.
Due to the deformation process exhibiting invariance,
the dispersion relation derived for localized plastic flow
auto-waves that are generated at the stages of easy glide
and linear work hardening has quadratic form, i.e.
2
~
1
~
k 
.
A decrease in the entropy of the deforming medium
strongly suggests that localized plasticity auto-waves are
processes involved in the self-organization of the me-
dium.
The localized plastic flow patterns are found to strictly
correspond to the respective flow stages in single crys-
tals and polycrystalline materials.
6. AKNOWLEDGEMENTS
This work was partly supported by the grant of RFBR (09-08-
00213-а).
REFERENCES
[1] Zuev, L.B. (2001) Wave phenomena in low-rate plastic
flow of solids. Annals of Physics, 10(11-12), 965-984.
[2] Zuev, L.B. (2007) On the waves of plastic flow loca-
lization in pure metals and alloys. Annals of Physics,
16(1), 286-310.
[3] Zuev, L.B. and Danilov, V.I. (1999) A self-excited wave
model of plastic deformation in solids. Philosophical
Magazine A, 79(1), 43-57.
[4] Zuev, L.B. and Semukhin, B.S. (2002) Some acoustic

L. B. Zuev et al. / Natural Science 2 (2010) 476-483
483
483
properties of a deforming medium. Philosophical Maga-
zine A, 82(6), 1183-1193.
[5] Zemskov, V.P. and Loskutov, A.Y. (2008) Oscillatory
traveling waves in excitable media. Journal of Experi-
mental and Theoretical Physics, 107(2), 344-349.
[6] Aifantis, E.C. (1996) Nonlinearly, periodicity and patter-
ning in plasticity and fracture. International Journal of
Non-Linear Mechanism, 31(8), 797-809.
[7] Aifantis, E.C. (1995) Pattern formation in plasticity.
International Journal of Engineering Science, 33(15),
2161-2178.
[8] Aifantis, E.C. (2001) Gradient plasticity. In Lemaitre, J.,
Ed., Handbook of Materials Behavior Models, Acade-
mic Press, New York, 291-307.
[9] Haken, H. (1988) Information and self-organization. A
Macroscopic Approach to Complex Systems. Springer
Verlag, Berlin.
[10] Zuev, L.B., Gorbatenko, V.V. and Polyakov, S.N. (2002)
Instrumentation for speckle interferometry and techni-
ques for investigating deformation and fracture. Procee-
dings of SPIE, 4900, 1197-1208.
[11] Kolsky, H. (1963) Stress waves in solid. Dover, New
York .
[12] Barannikova, S.A. (2004) Dispersion of the plastic strain
localization waves. Technical Physics Letters, 30(4),
338-340.
[13] Scott, A. (2003) Nonlinear science. University Press,
Oxford.
[14] Braun, O.M. and Kivshar, Y.S. (2004) The Frenkel-
Kontorova model. Springer, Berlin.
[15] Donnay, J.D.H. (1963) Crystal data. Determinate Tables,
Williams and Heintz Map Corp., Washington.
[16] Anderson, O.L. (1965) Determination and some applica-
tions of the isotropic elastic constants of polycrystalline
systems, obtained from single crystals data. In Mason, W.
P., Ed., Physical Acoustics: Principles and Methods, 3B,
Academic Press, New York, 43-95.
[17] Dirac, P.A.M. (1978) Directions in physics. John Wiley
and Sons, New York.
[18] Al’shits, V.I. and Indenbom, V.L. (1975) Phonon and
electron drag of dislocations. Soviet Physics-Uspekhi,
115(18), 3-39.
[19] Nowick, A.S. and Berry, B.S. (1972) Anelastic relaxa-
tion in crystalline solids. Academic Press, New York.
[20] Kadomtsev, B.B. (1994) Dynamics and information.
Physics-Uspekhi, 164(7), 449-530.
[21] Seeger, A. (1957) Mechanism of glide and work-harde-
ning in face-centered cubic and hexagonal close packed
metals. In Fisher, J.C., Ed., Dislocations and Mechanical
Properties of Crystals, John Wiley and Sons, Inc., New
York, 243-329.
[22] Ashcroft, N. and Mermin, N. (1976) Solid state physics.
Holt, Rinehart and Winston, New York.
[23] Aifantis, E.C. and Gerberich W.W. (1975) A theoretical
review of stress relaxation testing. Materials Science and
Engineering, 21(4), 107-113.
[24] White, R.M. and Geballe, T.H. (1979) Long range order
in solids. Academic Press, New York.
[25] Zuev, L.B., Danilov, V.I. and Barannikova, S.A. (2008)
Plastic flow, necking and failure in metals, alloys and
ceramics. Materials Science and Engineering A, 483-484,
223-227.