World Journal of Mechanics, 2012, 2, 61-76
doi:10.4236/wjm.2012.22008 Published Online April 2012 (http://www.SciRP.org/journal/wjm)
Thermal Fatigue Life Estimation and Fracture Mechanics
Studies of Multilayered MEMS Structures Using a
Sub-Domain Approach
Angelo Maligno1,2, David Whalley1, Vadim Silberschmidt1
1Wolfson School of Mechanical and Manufacturing Engineering, Loughborough University, Loughborough, UK
2Zentech International Ltd., London, UK
Received December 4, 2011; revised February 7, 2012; accepted February 20, 2012
ABSTRACT
This paper is concerned with the application of a Physics of Failure (PoF) methodology to assessing the reliability of
Micro-Electro-Mechanical-System (MEMS) switches. Numerical simulations, based on the finite element method
(FEM) using a sub-domain approach, were performed to examine the damage onset (e.g. yielding) due to temperature
variations and to simulated the crack propagation different kind of loading conditions and, in particular, thermal fatigue.
In this work remeshing techniques were employed in order to understand the evolution of initial flaws due, for instance,
to manufacturing processes or originated after thermal fatigue.
Keywords: Sub-Domain; FEM; Thermal Fatigue; Adaptive Remeshing
1. Introduction
Physics of Failure (PoF) methodologies have become
recently reliable tools for evaluating the risks of failure
of micro electro mechanical system (MEMS). For this
reason the Polynoe Programme is committed at improv-
ing the understanding, the modelling and the prediction
of the reliability of MEMS switches through a PoF ap-
proach [1]. Typical failure modes observed in MEMS
devices and their packages include fatigue, interface de-
lamination, and die cracking. In particular, delamination
is a condition that occurs when a materials interface loses
its adhesive bond. It can arise as the result of fatigue in-
duced by the long term cycling of structures with mis-
matched coefficients of thermal expansion. The effects of
delamination can be catastrophic and the loss of mass
might modify the mechanical characteristics, e.g. reso-
nant frequency of a structure [2]. This research aims,
firstly, to understand the effects of temperature variations
as a possible cause of damage, such as yielding in the
metal layers, and subsequent failure (e.g. interfacial de-
lamination, fracture) in multilayered MEMS packages.
The particular MEMS switches considered in this work
are DC switches, but the methodology is applicable to a
range of devices manufactured using similar technology.
However, the construction of full finite element models
of MEMS devices, such as DC MEMS switches, which
are detailed enough to accurately resolve the stresses
within each region of the model is difficult due to their
complex geometry. In general, simulation of full scale
models of the MEMS structures describe the device be-
haviour under different loading conditions and neglect
the determination of localised (internal and external)
stress/strain [2], which might trigger various modes of
failure such as interfacial delamination, fracture, etc.
Hence, an accurate determination of local stresses can be
achieved by the use of a representative sub-domain in
which the effect of the global stress/strain field at the
local micro-structural scale of the device can be com-
puted more accurately [3]. The sub-domain adopted in
this study is three-dimensional (3D), with the aim of
achieving an accurate and realistic tri-axial stress/strain
distribution within the FE model. This methodology al-
lows a detailed understanding of the effects of thermal
loading conditions on the stress/strain distribution at mi-
cro-structural level and in particular near the materials
interfaces [4,5]. The second part of this study aims to
simulate the crack evolution in metal layers in which the
high stress gradients, due to the material mismatch,
might lead to inter layer damage with the presence of
cracks. An automatic adaptive remeshing technique was
already implemented successfully by Maligno et al. [6]
to model 3D crack growths. In this paper a conceptual
model is presented for a software framework, based on
the remeshing tool Zencrack combined with the widely
used commercial FE code ABAQUS, which allows effi-

A. R. MALIGNO ET AL. 62
cient and automatic simulation of non-planar 3D crack
propagation.
2. MEMS Switch Description
DC Switch Presentation
The MEMSCAP DC switches are bi-stable and consume
no power in either ON or OFF position. The actuators
(Figure 1) are modified form of a thermal actuator,
which is commonly known as “heatuator”.
The “heatuator” is a U-shaped (Figure 2) structure
that uses differential thermal expansion to achieve mo-
tion along the wafer surface [1]. When a voltage is ap-
plied to the terminals, current flows through the device.
However, because of the different widths, the current
density is unequal in the two arms.
This leads to a different rate of Joule heating in the
two arms, and thus to different amounts of thermal ex-
pansion. The thin arm is often referred to as the hot arm,
and the wide arm is often referred to as the cold arm. In
this design the “cold” beam, which is used to carry the
electrical signal, is electrically isolated from the “hot”
beam, which is actuating the switch. In order to make a
latching switch, two such beams are used. The switch is
fabricated in the “open” position and in order to close the
switch an appropriate switching sequence, i.e. heating
sequence of the two actuators, is performed.
Figure 1. MEMSCAP DC switch. Green beams are the pas-
sive arms used to carry the electrical signal. Red beams are
the active arms used to actuate the switch.
Figure 2. Heatuator principle [1].
3. 3D Finite Element Modelling
3.1. Micromechanical Model
A simplified numerical model of the MEMS switches
used in the Polynoe Programme is shown in Figures 3
and 4 [1]. Nevertheless, to achieve reliable and detailed
information about the effects of thermal changes within
the multilayered structure, the numerical model shown in
Figure 1 is not suitable. In fact, very large numbers of
nodes are required in the mesh to detect the failure onset
(e.g. yielding). Therefore, a sub-domain approach has
been preferred to a full scale model.
The sub-domain used in these studies in order to ex-
amine the effects of thermal variation in the MEMS
structure and, in particular, to estimate the life of the me-
tal layers is depicted in Figures 5 and 6.
Although the numerical model is particularly simple, it
allows the use of great details. In fact, it is possible to
employ a mesh with a large number of solid brick ele-
ments (more than 300,000) with a quadratic interpolation
in order to detect, as accurately as possible, the yielding
onset in the metal layers and brittle failure within the
Figure 3. 3D representation of a multilayered MEMS switch
used in this research.
Figure 4. Detail of the cantilever beams.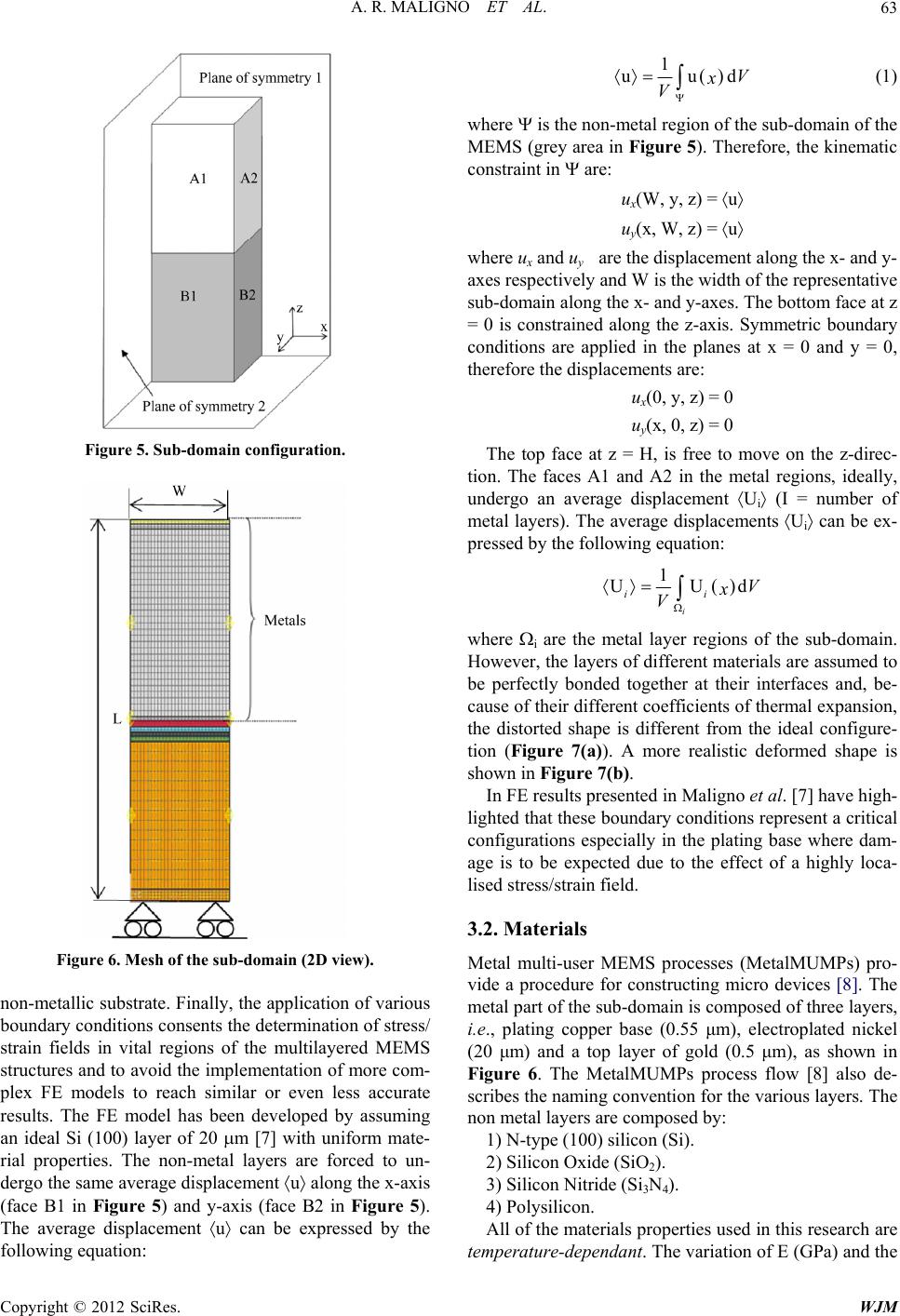

A. R. MALIGNO ET AL. 63
Figure 5. Sub-domain configuration.
Figure 6. Mesh of the sub-domain (2D view).
non-metallic substrate. Finally, the application of various
boundary conditions consents the determination of stress/
strain fields in vital regions of the multilayered MEMS
structures and to avoid the implementation of more com-
plex FE models to reach similar or even less accurate
results. The FE model has been developed by assuming
an ideal Si (100) layer of 20 m [7] with uniform mate-
rial properties. The non-metal layers are forced to un-
dergo the same average displacement u along the x-axis
(face B1 in Figure 5) and y-axis (face B2 in Figure 5).
The average displacement u can be expressed by the
following equation:

1
uud V
x
V
  (1)
where  is the non-metal region of the sub-domain of the
MEMS (grey area in Figure 5). Therefore, the kinematic
constraint in  are:
ux(W, y, z) = u
uy(x, W, z) = u
where ux and uy are the displacement along the x- and y-
axes respectively and W is the width of the representative
sub-domain along the x- and y-axes. The bottom face at z
= 0 is constrained along the z-axis. Symmetric boundary
conditions are applied in the planes at x = 0 and y = 0,
therefore the displacements are:
ux(0, y, z) = 0
uy(x, 0, z) = 0
The top face at z = H, is free to move on the z-direc-
tion. The faces A1 and A2 in the metal regions, ideally,
undergo an average displacement Ui (I = number of
metal layers). The average displacements Ui can be ex-
pressed by the following equation:

1
UU
i
ii
V
x
V
 d
where i are the metal layer regions of the sub-domain.
However, the layers of different materials are assumed to
be perfectly bonded together at their interfaces and, be-
cause of their different coefficients of thermal expansion,
the distorted shape is different from the ideal configure-
tion (Figure 7(a)). A more realistic deformed shape is
shown in Figure 7(b).
In FE results presented in Maligno et al. [7] have high-
lighted that these boundary conditions represent a critical
configurations especially in the plating base where dam-
age is to be expected due to the effect of a highly loca-
lised stress/strain field.
3.2. Materials
Metal multi-user MEMS processes (MetalMUMPs) pro-
vide a procedure for constructing micro devices [8]. The
metal part of the sub-domain is composed of three layers,
i.e., plating copper base (0.55 μm), electroplated nickel
(20 μm) and a top layer of gold (0.5 μm), as shown in
Figure 6. The MetalMUMPs process flow [8] also de-
scribes the naming convention for the various layers. The
non metal layers are composed by:
1) N-type (100) silicon (Si).
2) Silicon Oxide (SiO2).
3) Silicon Nitride (Si3N4).
4) Polysilicon.
All of the materials properties used in this research are
temperature-dependant. The variation of E (GPa) and the

A. R. MALIGNO ET AL. 64
(a)
(b)
Figure 7. Ideal deformed shape (a) and more realistic defor-
mation of the SUB-DOMAIN; (b) The shadowed area re-
presents the unreformed shape.
coefficient of thermal expansion
 (˚C–1) with the tem-
perature for the nickel are [9-14]:
1) E(T)  230 × (1 – 0.000286T) (2)
2)
 (T) = 13 × 10–6 × (1 + 0.000343T) (3)
The nickel layer undergoes a linear kinematic harden-
ing material behaviour and the kinematic strain harden-
ing rate H (i.e. the slope of the uniaxial stress-strain
curve beyond yielding) has been experimentally evalu-
ated to be 4 GPa (2%). For the plating copper (Cu) base,
the material properties of the passivated copper films and
the kinematic hardening model been considered. The li-
near dependence of initial yield strength with tempera-
ture can be described by the following relationship [17]:
0
0
1
y
T
T






d
(4)
where 
y is the initial yield strength, T is temperature,
and

0 and T0 are reference constants. For passivated
copper films, reliable results have been obtained with 
0
= 305 MPa, T0 = 1090 K and H = 77 GPa [12]. For the
thin gold layer an elastic-perfectly plastic constitutive
model has been adopted to simulate the material beha-
viour. The materials properties obtained by several sources,
e.g. [9-14], are summarised in Table 1.
3.3. Loading Conditions for Thermal Fatigue
Analysis
In the present analysis, the temperature cycle applied to
estimate the life of the multilayered sub-domain under
the described boundary condition is:
 Cyclic thermal loading: from 0˚C to 150˚C.
Moreover, effects of residual stresses arising during
manufacturing processes were considered. In fact, elec-
troplated metal thin films comprising nickel, copper and
gold are commonly used for micro-electromechanical
systems (MEMS) as they provide a simple technology
with superior material properties and device performances.
It is known that the microstructure and mechanical pro-
perties of a plated thin film depend upon the plating con-
ditions such as temperature, concentration and current
density [15]. Thus, in this study, an attempt to understand
the effect of temperature on residual stress build-up has
been investigated. Although electroplating processes, in
general, take place at relatively low temperatures (140˚C)
[8] other manufacturing process, such as packaging, might
reach higher temperatures [2]. In Maligno et al. [7] was
shown that, in general, starting from temperatures of
circa 80˚C, yielding processes are likely to occur in the
plating base (Cu layer). Therefore, to take into account
the effect of the fabrication process, the loading condi-
tions include a thermal cooling from 100˚C to 0˚C fol-
lowed by a cyclic thermal loading from 0˚C to 150˚C.
The thermal cooling has been applied to each layer of the
MEMS structure. Moreover, the metal and non-metal
layers undergo the same time-independent cooling rate.
The materials are assumed to be stress free. The total
induced strain of the layers due to thermal cooling can be
expressed as:
d()
ijij TT



where d 
ij is the total strain increment, α(T) the thermal
expansion coefficient which is dependent on the tem-
perature, dT the temperature change and 
ij is the Kro-
necker delta.
3.4. Loading Conditions for Delamination
Analysis
The crack propagation studies are based on the linear
elastic fracture mechanics (LEFM) approach. The sub-
domain used in the fracture mechanics studies has been
slightly modified (Figure 8) by adding a portion of a
cantilever beam of DC MEMS switches (Figure 6). The
use of a modified numerical model was necessary to
avoid conflicts during the remeshing procedure which
caused distorted elements. This was due to the addition

A. R. MALIGNO ET AL. 65
Table 1. Mechanical and thermal properties of the MEMS materials.
Ni Cu Au SiO2 Si3N4 Si Polysilicon
E
(GPa)
20˚C
400˚C
Equation
(2)
110
93
75
59.7
71.4
71.4
260
260
130
130
160
160
 20˚C
400˚C
0.31
0.31
0.3
0.3
0.42
0.42
0.16
0.16
0.25
0.25
0.28
0.28
0.23
0.23
 (T)
(10–6 × ˚C–1)
20˚C
400˚C
Equation
(3)
17
19.6
14.2
15.02
0.52
0.73
3.2
4.8
3.1
4.7
2.6
4.2

y(metals)

ult(non metals)
(
MPa
)
20˚C
400˚C
370
143
Equation
(4)
155
52 486 460 3790 2000
Figure 8. Applied displacements.
of several extra nodes on the faces placed on the plane of
symmetry-2 and on face A2 and B2 (Figure 5). In the
present analysis, initially two temperature variations have
been applied in order to investigate the effect of the
boundary conditions on failure onset within the multi-
layer sub-domain, namely:
 Cyclic thermal loading: from 0˚C to 150˚C.
 Cyclic thermal loading: from –55˚C to 150˚C.
Also, a cyclic displacement in the z-direction has been
superimposed to the cyclic thermal load to take into ac-
count the higher strains measured in the plastic FE
analyses and, mainly, to consider the displacements of
the cantilever beam during the DC MEMS switches func-
tioning life, as described in the MEMS mission profiles.
Two different displacements have been applied:
 Axial Displacement (z-direction): 0.1 m and 0.0033
m (Figure 8(a)).
 Bending Displacement (z-direction): 0.1 m and 0.0033
m (Figure 8(b)).
The value of 0.1 m has been observed during the
non-linear numerical analyses and it is has been applied
in this study to understand whether the structure is able
to withstand such a high displacement with minimum
damage. The value 0.0033 m, which corresponds at
circa 0.6% of the copper film thickness, represents the
maximum axial displacement that should be allowed in
proximity of the anchorage region during operational
service.
4. Local Stress Analysis
Yielding is detected at the temperature of approximately
65˚C in the copper plating base. The FE analyses have
shown that the applied loading and boundary conditions
are of vital importance on the yielding onset. The Cu
plating base undergoes severe stress concentration at the
interface with the silicon. Due to the effect of the highly
stiffer non-metallic substrates the Cu film shows only
totally negligible displacement at the Cu/silicon interface.
The high interfacial stresses generate the initial yielding
onset and, a probable, successive interfacial delamination.
The trend of the von Mises and Tresca stresses along the
edge of the sub-domain are shown Figure 9 at Cu/silicon
interface. FE results have proven that the Tresca failure
criterion is more conservative (circa 13.5%) than the von
Mises criterion.
According to the two failure criteria the corner of the
sub-domain at the Cu/silicon and the edges of the Cu thin
film, at Cu/silicon interface, are particularly at risk of
failure. The Cu/Ni interface displays lower levels of
stress (at the same temperature) and no yielding has been
detected within the gold (Au) and nickel (Ni) film layers
(Figure 10).
5. Thermal Cycle Analysis
Critical combinations of thermal loadings and boundary
conditions might lead to damage (such interfacial dela-
mination) in MEMS packages. The analyses have shown
that the most critical area is represented by the thin cop-
per plating base and in particular at the interface with the
polysilicon in which high stress gradients arise. Similar
results have been reached by research partners within the
Polynoe programme, which investigated, experimentally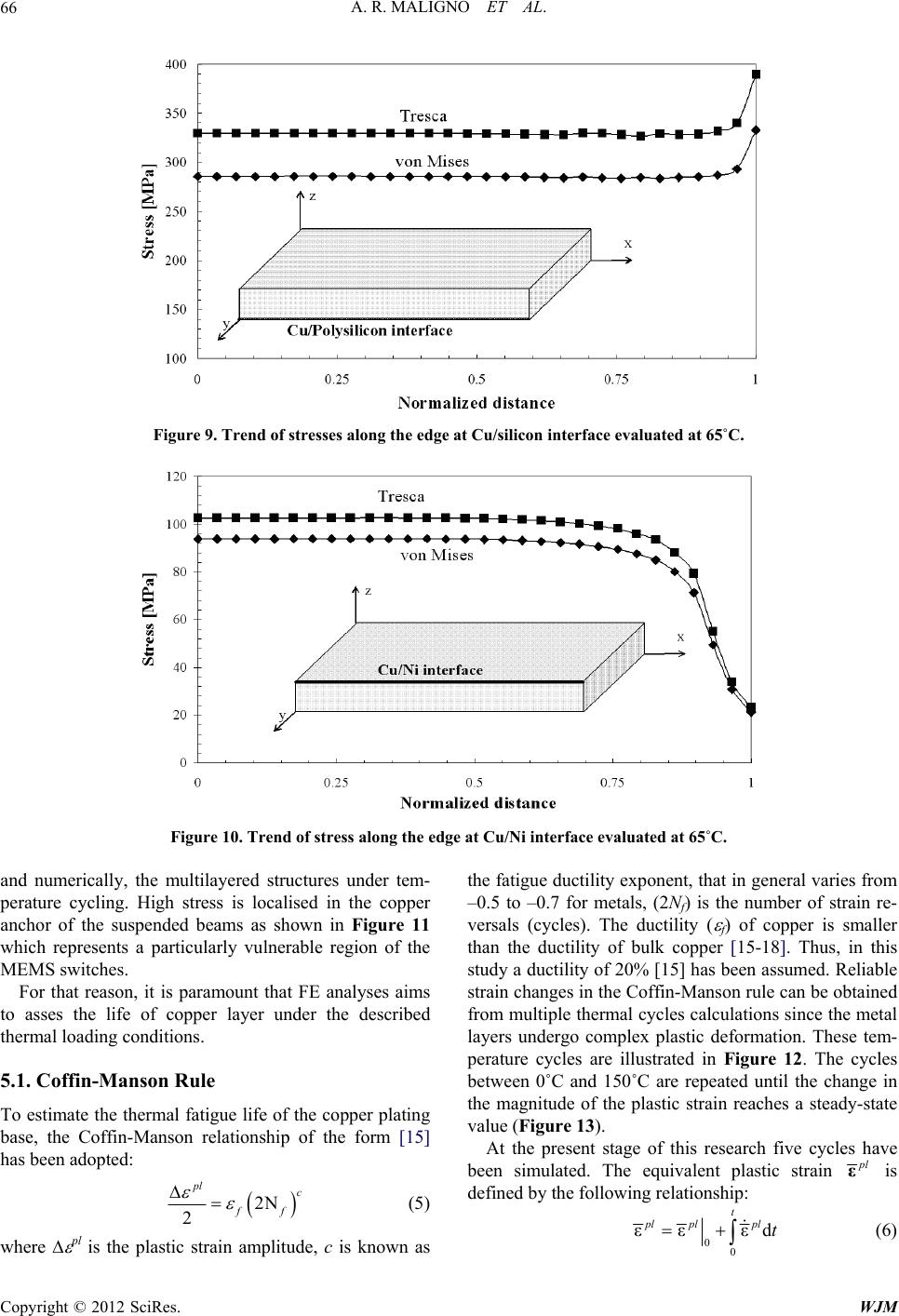

A. R. MALIGNO ET AL. 66
Figure 9. Trend of stresses along the edge at Cu/silicon interface evaluated at 65˚C.
Figure 10. Trend of stress along the edge at Cu/Ni interface evaluated at 65˚C.
and numerically, the multilayered structures under tem-
perature cycling. High stress is localised in the copper
anchor of the suspended beams as shown in Figure 11
which represents a particularly vulnerable region of the
MEMS switches.
For that reason, it is paramount that FE analyses aims
to asses the life of copper layer under the described
thermal loading conditions.
5.1. Coffin-Manson Rule
To estimate the thermal fatigue life of the copper plating
base, the Coffin-Manson relationship of the form [15]
has been adopted:

2N
2
pl c
ff
 

(5)
where  
pl is the plastic strain amplitude, c is known as
the fatigue ductility exponent, that in general varies from
–0.5 to –0.7 for metals, (2Nf) is the number of strain re-
versals (cycles). The ductility ( 
f) of copper is smaller
than the ductility of bulk copper [15-18]. Thus, in this
study a ductility of 20% [15] has been assumed. Reliable
strain changes in the Coffin-Manson rule can be obtained
from multiple thermal cycles calculations since the metal
layers undergo complex plastic deformation. These tem-
perature cycles are illustrated in Figure 12. The cycles
between 0˚C and 150˚C are repeated until the change in
the magnitude of the plastic strain reaches a steady-state
value (Figure 13).
At the present stage of this research five cycles have
been simulated. The equivalent plastic strain
p
l
ε is
defined by the following relationship:
00
εε εd
t
plplpl t
 (6)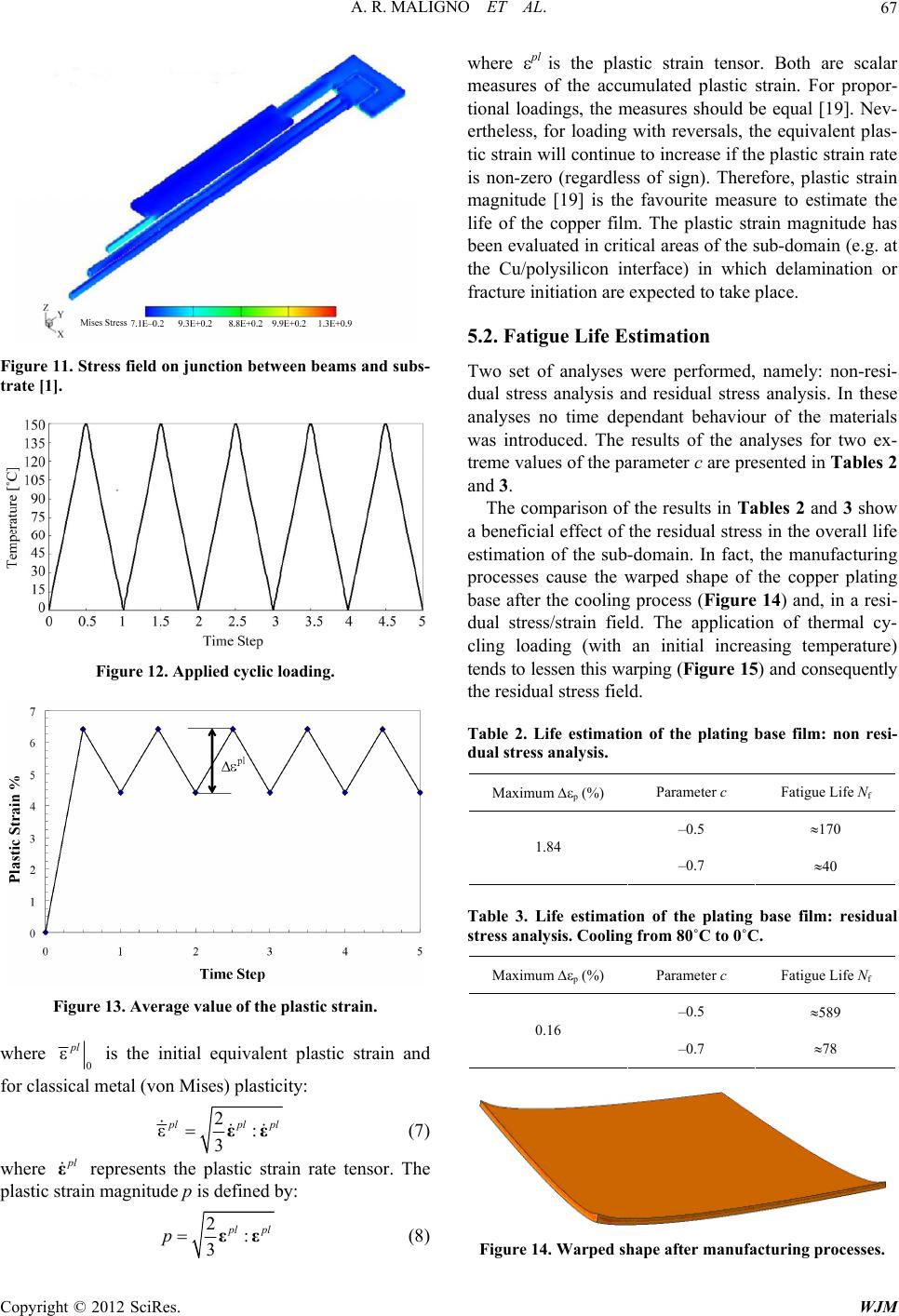

A. R. MALIGNO ET AL. 67
Figure 11. Stress field on junction between beams and subs-
trate [1].
Figure 12. Applied cyclic loading.
Figure 13. Average value of the plastic strain.
where 0 εpl is the initial equivalent plastic strain and
for classical metal (von Mises) plasticity:
2
ε:
3
p
lpl
εε

pl
(7)
where
p
l
ε
 represents the plastic strain rate tensor. The
plastic strain magnitude p is defined by:
2:
3
p
lpl
pεε (8)
where pl
is the plastic strain tensor. Both are scalar
measures of the accumulated plastic strain. For propor-
tional loadings, the measures should be equal [19]. Nev-
ertheless, for loading with reversals, the equivalent plas-
tic strain will continue to increase if the plastic strain rate
is non-zero (regardless of sign). Therefore, plastic strain
magnitude [19] is the favourite measure to estimate the
life of the copper film. The plastic strain magnitude has
been evaluated in critical areas of the sub-domain (e.g. at
the Cu/polysilicon interface) in which delamination or
fracture initiation are expected to take place.
5.2. Fatigue Life Estimation
Two set of analyses were performed, namely: non-resi-
dual stress analysis and residual stress analysis. In these
analyses no time dependant behaviour of the materials
was introduced. The results of the analyses for two ex-
treme values of the parameter c are presented in Tables 2
and 3.
The comparison of the results in Tables 2 and 3 show
a beneficial effect of the residual stress in the overall life
estimation of the sub-domain. In fact, the manufacturing
processes cause the warped shape of the copper plating
base after the cooling process (Figure 14) and, in a resi-
dual stress/strain field. The application of thermal cy-
cling loading (with an initial increasing temperature)
tends to lessen this warping (Figure 15) and consequently
the residual stress field.
Table 2. Life estimation of the plating base film: non resi-
dual stress analysis.
Maximum p (%) Parameter c Fatigue Life Nf
–0.5 170
1.84
–0.7 40
Table 3. Life estimation of the plating base film: residual
stress analysis. Cooling from 80˚C to 0˚C.
Maximum p (%) Parameter c Fatigue Life Nf
–0.5 589
0.16
–0.7 78
Figure 14. Warped shape after manufacturing processes.

A. R. MALIGNO ET AL. 68
Figure 15. Reduced deformed shape at increasing tempera-
tures.
6. FE Modelling of Automated Crack
Growth
In the delamination mechanics theory applied to film and
multi-layers, of particular interest are the Mode-I crack-
ing in films/layers driven by stress gradients. Therefore,
the evaluated high stress gradient present in the copper
plating base are likely trigger a Mode-I crack in the thin
layer which could propagate within the structure and,
eventually, lead to the drastic failure of the MEMS de-
vices. The purpose of this research was to understand the
crack behaviour in thin films such as the copper plating
base and, mainly, to understand the effect of the tem-
perature variation on the crack evolution. In order to si-
mulate the fatigue crack propagation in multi-layered
MEMS structures, the software Zencrack in combination
with the FE code ABAQUS was used. In this research
the software has been modified by introducing new algo-
rithms to describe, as accurately as possible, crack evolu-
tion in thin films and to avoid mesh and structural distor-
tion during the remeshing. The interfacial fracture tough-
ness of the copper has been adopted as the reference pa-
rameter to evaluate the catastrophic failure (e.g. delami-
nation) of the copper film. The interfacial fracture tough-
ness of the copper, used in this study, ranges from 0.4 to
2.61 J/m2 [20]. These values take into account the mate-
rial properties of copper at micro-level and, in particular,
different grain sizes.
6.1. Crack Growth Criteria
In order to predict linear elastic fracture mechanics
(LEFM) crack growth using FE method, three basic pa-
rameters are required: stress intensity factors (SIF), crack
propagation direction (CPD) and crack growth material
models, for example, the Paris equation [21]. There are
several approaches to calculating SIFs such as: the crack
tip opening displacement (CTOD) approach [22], the
crack tip stress field approach [23] and the SIF extraction
method from J-integral [24]. In the present work the SIFs
are extracted from the J-integral using the method of
Asaro and Shih [25], based on the following equation:

22 2
11
2

I
II III
JGK KK
EG
 (9)
where 
2
1
EE

 for three-dimensional problems.
The quarter-point node technique is used by Zencrack to
model the crack-tip singularity. Under mixed mode con-
ditions it is necessary to introduce an equivalent stress
intensity factor, Keq, considering Mode-I, II and III si-
multaneously. Several formulae have been proposed for
Keq and the most commonly used expression is:

22 2
1
eqI IIIII
K
KK K   (10)
In order to determine new crack front positions, the
CPD must be computed. There are several CPD criteria
available: the minimum strain density criterion, the maxi-
mum circumferential stress criterion and the maximum
energy release criterion. The maximum energy release
rate criterion or the G-criterion has been adopted in these
investigations. The G-criterion states that a crack will
grow in the direction of maximum energy release rate.
The CPD,  = 
o, is then determined by:
2
d0,
d
d0.
d
o
o
G
G












(11)
Numerous numerical techniques can be used to com-
pute G such as the path independent J-integral [24,25]
and the virtual crack extension (VCE) method [26,27].
The VCE method, which was already successfully em-
ployed in Maligno et al. [6], was also applied in this re-
search.
Virtual Crack Extension Directions
To determine the crack direction a “normal plane” can be
defined at any node on a 3D crack front. This is a plane
that is orthogonal to the crack front tangent at the node.
A series of virtual crack extensions in the normal plane
will produce a distribution of energy release rates. This is
shown schematically in Figure 16 as energy release rate
values G1 to G7. At some angle to the local crack plane
the energy release rate will be a maximum. Gmax denotes
this maximum energy release rate. The value of Gmax and
the corresponding angle is calculated for use in crack
growth prediction.
6.2. Adaptive Remeshing Method
A crucial problem in 3D fracture mechanics is related to
mesh generation for the FE analysis. The approach that
has been adopted in this research is the use of a “sub
modeling” strategy which models the details of the crack
region. In Figure 17 is presented the use of the “sub
modeling” methodology in generating a cracked mesh
from a user-supplied intact component. The method
works by replacing one or more elements in the un-
cracked mesh by “crack-blocks” that contain sections of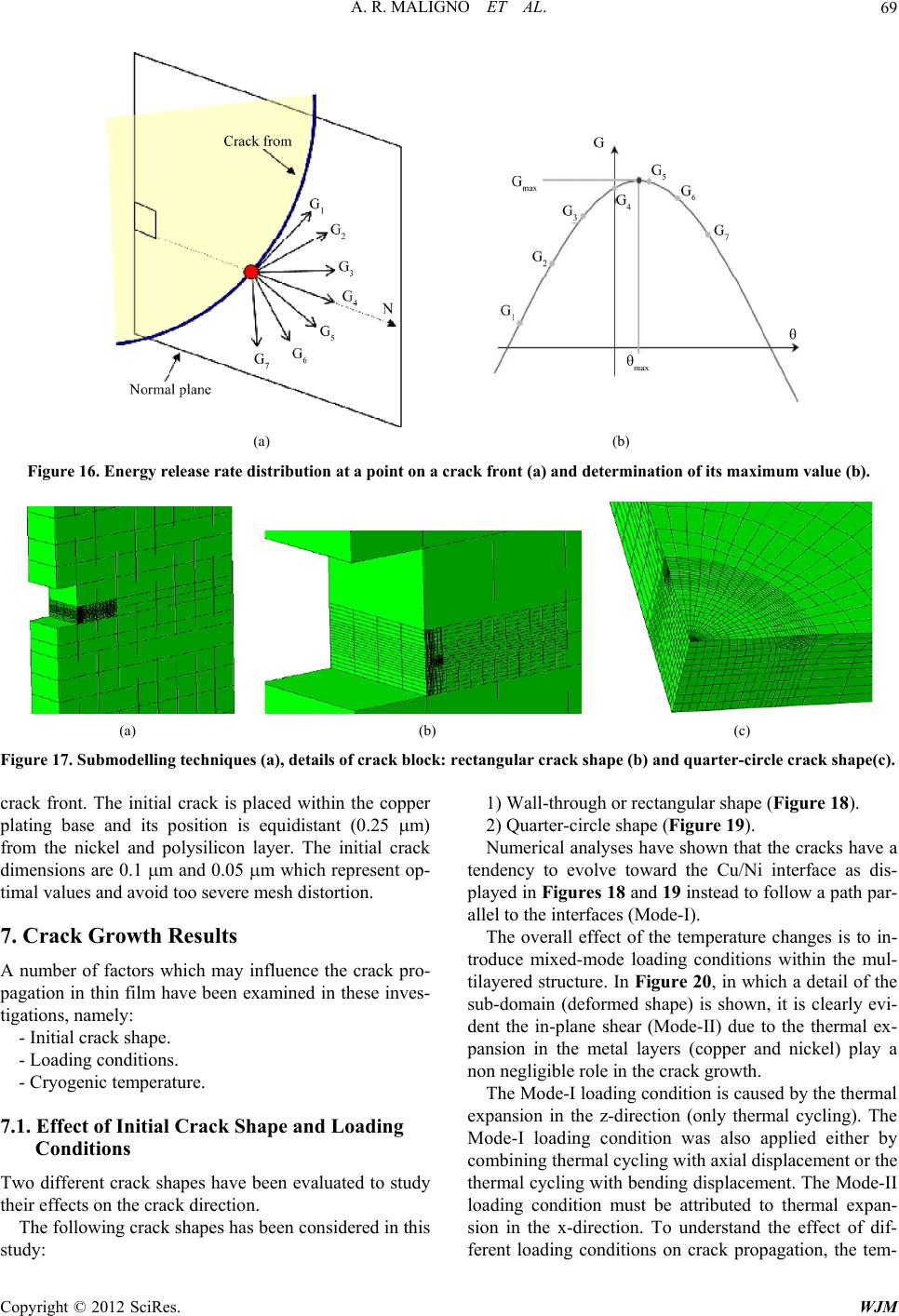

A. R. MALIGNO ET AL. 69
(a) (b)
Figure 16. Energy release rate distribution at a point on a crack front (a) and determination of its maximum value (b).
(a) (b) (c)
Figure 17. Submodelling techniques (a), details of crack block: rectangular crack shape (b) and quarter-circle crack shape(c).
1) Wall-through or rectangular shape (Figure 18). crack front. The initial crack is placed within the copper
plating base and its position is equidistant (0.25 m)
from the nickel and polysilicon layer. The initial crack
dimensions are 0.1 m and 0.05 m which represent op-
timal values and avoid too severe mesh distortion.
2) Quarter-circle shape (Figure 19).
Numerical analyses have shown that the cracks have a
tendency to evolve toward the Cu/Ni interface as dis-
played in Figures 18 and 19 instead to follow a path par-
allel to the interfaces (Mode-I).
7. Crack Growth Results The overall effect of the temperature changes is to in-
troduce mixed-mode loading conditions within the mul-
tilayered structure. In Figure 20, in which a detail of the
sub-domain (deformed shape) is shown, it is clearly evi-
dent the in-plane shear (Mode-II) due to the thermal ex-
pansion in the metal layers (copper and nickel) play a
non negligible role in the crack growth.
A number of factors which may influence the crack pro-
pagation in thin film have been examined in these inves-
tigations, namely:
- Initial crack shape.
- Loading conditions.
- Cryogenic temperature. The Mode-I loading condition is caused by the thermal
expansion in the z-direction (only thermal cycling). The
Mode-I loading condition was also applied either by
combining thermal cycling with axial displacement or the
thermal cycling with bending displacement. The Mode-II
loading condition must be attributed to thermal expan-
sion in the x-direction. To understand the effect of dif-
ferent loading conditions on crack propagation, the tem-
7.1. Effect of Initial Crack Shape and Loading
Conditions
Two different crack shapes have been evaluated to study
their effects on the crack direction.
The following crack shapes has been considered in this
study:

A. R. MALIGNO ET AL. 70
(a)
(b)
Figure 18. Rectangular crack shape: initial crack (a), final
crack growth (b).
(a)
(b)
Figure 19. 1/4 circle crack shape: initial crack (a), final
crack growth (b).
Figure 20. Mixed mode loading introduced by the tempera-
ture variation in the multilayered MEMS structure.
poral evolution of the nodes positioned on the crack front
was monitored with a particular attention to the nodes
placed on the boundaries of the crack blocks (Figures 21
and 22). The overall results of various combinations of
loading conditions for a displacement of 0.0033 m and
Gc = 2.61 J/m2 are summarised in Tables 4 and 5.
The displacements on the z-direction 0.1 m magni-
tude lead to the severe immediate structural collapse of
the thin copper plating base. If Gc is 0.4 J/m2, i.e. the
minimum value found in [20], the structural failure of the
copper plating base is detected even during thermal cy-
cling.
Figure 21 shows the values of the energy release rate
during thermal cycling. Because of the thin film structure
different kind of “crack blocks”, available in Zencrack,
have been used for mesh sensitivity studies. Very coarse
meshes give, in general, misleading results. In fact the
crack blocks used in this study are “tied” to the rest of
mesh [19] and high differences in the mesh density will
lead to erroneous stress fields within the crack blocks.
More significant in the numerical results was the en-
hancement of the software Zencrack. New algorithms
have allowed the possibility to obtain a more accurate
evaluation of fracture mechanics parameters (e.g. energy
Table 4. Results based on the calculated G for a rectangular
crack, displacement = 0.0033 m and Gc = 2.61 J/m2.
Loading Conditions Minimum Energy Release Rate
Thermal Cycling: 0˚C/150˚CG = 0.99 J/m2  Drastic failure
during crack evolution
Thermal Cycling: –55˚C/150˚CG = 0.721 J/m2  Drastic
failure during crack evolution
Thermal Cycling: 0˚C/150˚C
Axial Displacement
G = 9.16 J/m2  Instantaneous
structural collapse
Thermal Cycling: –55˚C/150˚C
Axial Displacement:
G = 12.8 J/m2  Instantaneous
structural collapse
Thermal Cycling: 0˚C/150˚C
Bending Displacement:
G = 0.117 J/m2  Long crack
evolution before failure
Thermal Cycling: –55˚C/150˚C
Bending Displacement:
G = 226.4 J/m2  Instantaneous
structural collapse
Table 5. Results based on the calculated G for 1/4 circle
crack, displacement = 0.0033 m and Gc = 2.61 J/m2.
Loading Conditions Minimum Energy Release Rate
Thermal Cycling: 0˚C/150˚CG = 1.13 J/m2  Drastic failure
during crack evolution
Thermal Cycling: –55˚C/150˚CG = 0.825 J/m2  Drastic failure
during crack evolution
Thermal Cycling: 0˚C/150˚C
Axial Displacement
G = 9.78 J/m2  Instantaneous
structural collapse
Thermal Cycling: –55˚C/150˚C
Axial Displacement:
G = 11.3 J/m2  Instantaneous
structural collapse
Thermal Cycling: 0˚C/150˚C
Bending Displacement:
G = 109.98 J/m2  Instantaneous
structural collapse
Thermal Cycling: –55˚C/150˚C
Bending Displacement:
G = 105.45 J/m2  Instantaneous
structural collapse

A. R. MALIGNO ET AL. 71
(a)
(b)
Figure 21. Trend of the energy release rate on boundary nodes under thermal cycle. Non-enhanced software (a), enhanced
software for thin film structures (b).
Figure 22. Trend of the energy release rate on boundary nodes: thermal cycle and axial displacement (0.1 m).

A. R. MALIGNO ET AL. 72
release rate) in particularly difficult geometries such as
thin film structures. The new data are shown in Figures
21(a) and (b). From Tables 4 and 5 it can be noted that
under thermal cycling, the multilayered structure of the
MEMS switches are unlikely to develop severe initial da-
mage (e.g. delamination) attributable to the crack growth,
driven by the high stress gradient, within the anchor layer
of copper. Nevertheless, the application of a coupled
thermo-mechanical loads implies the drastic increase of
the critical energy release rate at the initial conditions (i.e.
initial crack 0.1 m). The lowest calculated increase
(coupled thermal/axial cycling) of the energy release rate
is 300% higher than the Gc evaluated during the thermal
cycling loading. Furthermore, the stress intensity factors
KI and KII, which are related to Mode-I loading and
Mode-II loading respectively, are of the same order of
magnitude. In the coupled thermal/displacement loading
(Figure 23), the stress intensity factor KI is circa 70%
higher than the KI achieved during the thermal cycling as
displayed in Figure 24.
Hence, Mode-I loading becomes more influent with
respect to Mode-II loading and, the overall result of an
increasing KI (and consequently the relative energy re-
lease rate GI) is to reduce partially the effect of the mixed
mode loading. This effect is highlighted in Figure 25 in
which the crack paths of different loading conditions are
depicted. The effect of an increasing Mode-I loading is
represented by the tendency of the crack path to reduce
its slope toward the Cu/Ni interface and to develop par-
allel (pure Mode-I) to the copper layer interfaces. It is
worthwhile to notice that the KII value is not influenced
by the application of different loading conditions and its
magnitude remains in general at the same level.
In Figures 26 and 27, the trend of the energy release
rates related to the crack path of the loading conditions
described in Figure 25 are shown. It is worthwhile to
notice the particular behaviour of G for the coupled ther-
mal/bending cycling. The applied bending displacement
tends to reduce the stress field around the crack tip if the
crack shape is rectangular. This particular effect is not
present in circular crack shapes in which much higher
values are present.
Figure 23. Trend of the stress intensity factors: thermal cycling and axial displacement (0.1 m).
Figure 24. Trend of the stress intensity factors: thermal cycling (0.1 m).

A. R. MALIGNO ET AL. 73
(a) (b) (c)
Figure 25. Crack path for different loading conditions (rectangular crack shape). (a) Thermal cycling; (b) Thermal and axial
cycling; (c) Thermal and bending cycling.
Figure 26. Trend of the energy release rate in square crack (0.0033 m).
Figure 27. Trend of the energy release rate in rectangular and circular crack (0.0033 m).
The energy release rate, in the rectangular crack shape
case, remains constantly low and allows a crack propaga-
tion of circa 70% of the initial value 0.1 m. Unlike the
rectangular crack shape case, the quarter circle shape
(Table 5) does not allow any crack evolution and leads
to the drastic failure (e.g. stress-gradient originated de-
lamination) of the copper plating base.
7.2. Effect of Cryogenic Temperature
A critical parameter to consider in the design of MEMS
switches are the effect temperature dependant material
properties which have been, till now, investigated for a
range above 0˚C. Nevertheless, especially in aerospace
and defence applications it is necessary to examine the
effect of cryogenic temperatures. Therefore, the effect of
thermal cycling from –55˚C to 150˚C (according to the
mission profiles recommended by the Polynoe Pro-
gramme) was investigated. The FE simulations show the
crucial detrimental effect of cryogenic temperature on
the crack propagation (Figure 28) in coupled thermal/

A. R. MALIGNO ET AL. 74
Figure 28. Trend of the energy release rate with 1/4 circle crack and displacements of 0.0033 m.
displacement cyclic loading conditions whilst, in the
thermal cycling case the energy release rate still remains
confined to safe values as long as the Gc is greater than
0.825 J/m2 (Figure 28) which represents the initial value
of detected during thermal (cryogenic) cycling. Also, it
can be noticed that the cryogenic thermal cycling tends to
lower the initial value of the energy release rate. In fact,
the minimum value evaluated during thermal cycling
from 0˚C to 150˚C is circa 0.9 J/m2 (Figure 28).
This drastic delamination is also being investigated
experimentally. Preliminary accelerated tests have been
performed in order to estimate the maximum range of
temperature variations to use without cause catastrophic
damage (e.g. delamination). For the preliminary acceler-
ated tests a thermal shock approach was adopted. The
temperature ranges from 200˚C to –55˚C. The dwelling
time at 200˚C and –55˚C is one hour while, the transition
time from 200˚C to –55˚C is less than one minute. The
initial temperature of 200˚C was chosen to simulate the
effects of the packaging temperature. The surface mor-
phology of the DC MEMS presented in Figure 1 was
been examined before and after the thermal cycling. Ex-
perimental results show that drastic thermal variations
causes severe distortions, e.g. in the suspended beam,
after just few cycles (less than five cycles). Also delami-
nation is very likely to occur as high displacements in the
z-direction (Figure 29) were measured in proximity of
the anchorage between beams and substrate.
Although more detailed experimental tests are necessary
to fully understand the MEMS behaviour under tempera-
ture variation, the experimental tests confirms, in general,
the numerical results. In fact, the drastic change of tem-
perature implies rigorous displacements of the suspended
beams along the z-direction (Mode-I) and x-direction
(Mode-II) which leads to the damage onset such as crack
initiation and, to the following catastrophic propagation as
simulated in the delamination mechanics studies.
8. Conclusion
A FEM study has been performed on multilayered
MEMS structures to evaluate the reliability of these com-
ponents under different loading conditions and in par-
ticular, thermal fatigue. This study is based on a sub-
domain approach, therefore, only a tiny region of MEMS
switch, under various loading conditions, is considered.
The numerical simulations have shown that the most
vulnerable area of multilayered MEMS switches is rep-
resented by the copper plating base. Strong stress gra-
dients arises within the copper film due to the different
material behaviour between the Cu/Polysilicon interface
and Cu/Ni interface The life estimation of copper layer is
also influenced by the presence of residual stresses. More
refined fracture mechanics compared to the preliminary
studies [7] have demonstrated that the drastic failure of
the copper plating base may occur during thermal varia-
tion and it can cause the malfunctions of the DC MEMS
switches during the operational service. In these new
fracture mechanics studies a more refined mesh density
in the proximity of the initial flaws has been adopted and,
more importantly, the Zencrack code has been enhanced
to give more accuracy in particularly “squeezed” geome-
tries such as thin film layers. The results show that the
applied thermal variation implies higher values of the
energy release rate G than previously evaluated [7]. The
application of cryogenic thermal cycling is, in general,
slightly beneficial in terms of the reduction of the energy
release rate both for rectangular and the 1/4 circular
crack shape and in coupled (thermal and bending mo-
ment) loads with 1/4 circular crack shape. Cryogenic
temperatures lead to detrimental results in all the other
case in which coupled thermo-mechanical loading condi-
tions are applied and in particular when thermal and

A. R. MALIGNO ET AL. 75
(a)
(b)
Figure 29. Reference position (a) and measured displacements (b) of the beams after thermal cycling at anchor level.
bending moment are applied to a rectangular crack.
Moreover, the displacements applied at cryogenic tem-
perature are very likely to lead to instantaneous failures
of the internal MEMS structure and faults of the switches.
Further experimental tests have been planned to under-
stand the multilayered structure behavior under particu-
larly harsh loading conditions (e.g. thermal cycling in-
volving cryogenic temperatures) and to evaluate as accu-
rately as possible the critical energy release rate Gc and
the necessary parameters to carry out damage tolerance
studies. Finally, the comparison of different methods and
criteria for the determination of crack growth parameters is
also under evaluation.
9. Acknowledgments
This research is funded by the European Defence Agency
(EDA) through the POLYNOE Programme.
REFERENCES
[1] J. Dhennin and D. Lellouchi, “Implementation of Physics
of Failure for MEMS,” 2009.
http://polynoe.org/page1.htm
[2] T. Hsu, “MEMS and Microsystems,” 2nd Edition, Wiley,
New York, 2008.
[3] Y. Gu and T. Nakamura, “Interfacial Delamination and
Fatigue Life Estimation of 3D Solder Bumps in Flip-Chip
Packages,” Microelectronics Reliability, Vol. 44, No. 3,
2004, pp. 471-483. doi:10.1016/j.microrel.2003.11.002
[4] N. Kay, E. Madenci and S. Shkarayev, “Global/Local
Finite Element Analysis for Singular Stress Fields near
the Junction of Dissimilar Elastic and Elastic-Plastic Ma-
terials in Electronic Packages,” Proceedings Electronic
Components & Technology Conference, San Diego, 1999,
pp. 987-993.
[5] E. Madenci, S. Shkarayev and B. Sergeev, “Thermo-
Mechanical Stresses for a Triple Junction of Dissimilar
Materials: Global-Local Finite Element Analysis,” Jour-
nal of Theoretical Applied Fracture Mechanics, Vol. 30,
No. 103, 1998, pp. 103-117.
[6] A. R. Maligno, S. Rajaratnam, S. B. Leen and E. J. Wil-
liams, “A Three-Dimensional (3D) Numerical Study of
Fatigue Crack Growth Using Remeshing Techniques,”
Engineering Fracture Mechanics, Vol. 77, No. 11, 2010,
pp. 94-111.
[7] A. R. Maligno, D. Whalley, V. Silberschmidt, “Interfacial
Failure under Thermal Fatigue Loading in Multilayered
MEMS Structure,” Materials Science and Engineering,
Vol. 10, No. 1, 2010, Article ID: 012087.
[8] A. Cowen, “MetalMUMPs Design Handbook,” Revision
1.0, 2002.
http://www.memscap.com/__data/assets/pdf_file/0015/18
33/MetalMUMPs.DR.4.0.pdf
[9] D. Hill, W. Szyszkowski and E. Bordatchev, “On Mod-
eling and Computer Simulation of an Electro-Thermally
Driven Cascaded Nickel Micro-Actuator,” Sensors and
Actuators A, Vol. 126, No. 1, 2006, pp. 253-263.
doi:10.1016/j.sna.2005.09.030
[10] J. King, “Materials Handbook for Hybrid Micro Elec-
tronics,” Artech House, Boston, 1988.
[11] H. S. Ho, et al., “Measured Mechanical Properties of
LIGA Ni Structures,” Sensors and Actuators A, Vol. 103,

A. R. MALIGNO ET AL. 76
No. 1-2, 2003, pp. 59-63.
doi:10.1016/S0924-4247(02)00314-X
[12] Y. L. Shen, “Externally Constrained Plastic Flow in
Miniaturized Metallic Structures: A Continuum-Based
Approach to Thin Films, Lines, and Joints,” Progress in
Materials Science, Vol. 53, No. 5, 2008, pp. 838-891.
doi:10.1016/j.pmatsci.2008.03.001
[13] MEMS and Nanotechnology Exchange, “An information
Portal for the MEMS and Nanotechnology Community,”
2009. www.memsnet.org
[14] Online Materials Information Resource, 2009.
www.matweb.org
[15] K. Weinberg and W. H. Muller, “A Strategy for Damage
Assessment of Thermally Stressed Copper Vias in Micro-
electronic Printed Circuit Boards,” Microelectronics Re-
liability, Vol. 48, No. 1, 2008, pp. 68-82.
doi:10.1016/j.microrel.2007.03.003
[16] D. B. Barker and A. Dasgupta, “Thermal Analysis in
Plated-Through-Hole Reliability,” In: J. H. Lau, Ed.,
Thermal Stress and Strain in Microelectronic Packaging,
Van Nostrand Reinhold, New York, 1993.
[17] M. Niewczas and J. D. Embury, “Approaching the Theo-
retical Strength in Ductile Copper,” In: N. Zabaras, et al.,
Eds., The Integration of Material, Process and Product
Design, Taylor & Francis, Rotterdam, 1999.
[18] J. K. Luo, et al., “Young’s Modulus of Electroplated Ni
Thin Film for MEMS Applications,” Materials Letters,
Vol. 58, No. 17-18, 2004, pp. 2306-2309.
doi:10.1016/S0167-577X(04)00137-5
[19] Simulia, “ABAQUS User’s Manual,” Version 6.9, 2008.
[20] M. J. Cordill, T. Muppidi, N. R. Moody and D. F. Bahr,
“Effects of Microstructure on the Mechanical Properties
of Copper Films for High Aspect Ratio Structures,” Mi-
crosystems Technologies, Vol. 10, No. 6-7, 2004, pp.
451-455. doi:10.1007/s00542-004-0370-y
[21] P. C. Paris and F. Erdogan, “A Critical Analysis of Crack
Propagation Laws,” Journal of Basic Engineering, Vol.
85, No. 4, 1960, pp. 528-534. doi:10.1115/1.3656900
[22] P. C. Adrian and M. H Aliabadi, “Dual Boundary Ele-
ment Assessment of Three-Dimensional Fatigue Crack
Growth,” Engineering Analysis with Boundary Elements,
Vol. 28, No. 9, 2004, pp. 1157-1173.
doi:10.1016/j.enganabound.2004.01.005
[23] M. Guagliano and L. Vergani, “A Simplified Approach to
Crack Growth Prediction in a Crank Shaft,” Fatigue and
Fracture of Engineering Materials and Structures, Vol.
17, No. 5, 1994, pp. 1295-1306.
[24] J. R. Rice, “A Path Independent Integral and the Ap-
proximate Analysis of Strain Concentrations by Notches
and Cracks,” Journal of Applied Mechanics, Vol. 35, No.
2, 1968, pp. 379-386. doi:10.1115/1.3601206
[25] F. Z. Li, C. F. Shih and A. Needleman, “A Comparison of
Methods for Calculating Energy Release Rate,” Engi-
neering Fracture Mechanics, Vol. 21, No. 2, 1985, pp.
405-421. doi:10.1016/0013-7944(85)90029-3
[26] D. M. Parks, “The Virtual Crack Extension Method for
Nonlinear Material Behaviour,” Computer Methods in
Applied Mechanics and Engineering, Vol. 12, No. 3,
1977, pp. 353-364. doi:10.1016/0045-7825(77)90023-8
[27] H.G. DeLorenzi, “On the energy release rate and the
J-integral for 3D crack configurations,” Journal of Frac-
ture, Vol. 19, No. 3, 1982, 183-193.
doi:10.1007/BF00017129