Journal of Information Security, 2012, 3, 138-148
http://dx.doi.org/10.4236/jis.2012.32016 Published Online April 2012 (http://www.SciRP.org/journal/jis)
New Video Watermark Scheme Resistant to Super Strong
Cropping Attacks
Ming Tong, Tao Chen, Wei Zhang, Linna Dong
School of Electronic Engineerin, Xidian University, Xi’an, China
Received January 14, 2012; revised February 28, 2012; accepted March 20, 2012
ABSTRACT
Firstly, the nonnegative matrix factorization with sparseness constraints on parts of the basis matrix (NMFSCPBM) method is
proposed in this paper. Secondly, the encrypted watermark is embedded into the big coefficients of the basis matrix that
the host video is decomposed into by NMFSCPBM. At the same time, the watermark embedding strength is adaptively
adjusted by the video motion characteristic coefficients extracted by NMFSCPBM method. On watermark detection, as
long as the residual video contains the numbers of the least remaining sub-blocks, the complete basis matrix can be
completely recovered through the decomposition of the nonnegative matrix of the least remaining sub-blocks in residual
videos by NMFSCPBM, and then the complete watermark can be extracted. The experimental results show that the av-
erage intensity resistant to the various regular cropping of this scheme is up to 95.97% and that the average intensity
resistant to the various irregular cropping of this scheme is up to 95.55%. The bit correct rate (BCR) values of the ex-
tracted watermark are always 100% under all of the above situations. It is proved that the watermark extraction is not
limited by the cropping position and type in this scheme. Compared with other similar methods, the performance of
resisting strong cropping is improved greatly.
Keywords: Digital Watermarking; Cropping Attack; Geometric Attacks; Nonnegative Matrix Factorization (NMF);
Sparseness Constrain
1. Introduction
The watermarking robustness has been a focus in multi-
media research field, and how to resist geometric attacks
is the hotspot and difficulty of the study [1]. Geometric
attacks destroy the synchronization between the water-
mark and the videos, which seriously affect the robust-
ness of the watermarking and pose a deadly threat to the
watermarking security. At the same time, with the ap-
pearance and maturity of a variety of video signal proc-
essing tools, the video data can be cropped, copied and
tampered in various forms and different degrees much
more conveniently, faster and more casually. Especially
to strong cropping, the embedded watermark information
is cropped directly and enormously and the copyright of
digital video products is facing serious challenges. How
to extract and recover the complete watermark in residual
videos has always troubled researchers [2]. Consequently,
the research on video watermark methods resisting to
strong cropping attacks can help strengthening the copy-
right authentication and management, standardizing the
market of video products, and solving the technology
bottleneck problem of commercializing watermark, which
has important academic research value and extensive
market application prospect.
A four-level dual-tree complex wavelet transform (DT
CWT) is applied to every video frame of the host video
in [3], which embeds the watermark in the coefficients of
low frequency sub-band. This method takes the advan-
tage of perfect reconstruction, shift invariance, and good
directional selectivity of DT CWT, and can resist the
cropping attacks with a certain strength. In [4], the wa-
termark is embedded into 8 × 8 sub-blocks of each
I-frame, which is robust to row and column cropping
attacks with small strength. Since the geometrical distor-
tions operations for every frame along the time axis in a
video sequence are the same [5], the watermark is em-
bedded into the same position in the video frame by
modifying the pixels of texture complex or sports intense
area. But the information of the watermarks embedded
by this method is less, and the robustness is greatly in-
fluenced by host carrier characteristics. So this method
cannot resist cropping attacks. In [6], the watermark is
embedded into the singular value of the coefficient ma-
trix of nonnegative matrix factorization (NMF). This
method is robust to noise, filtering and other general at-
tacks, but cannot resist strong cropping attacks. Theo-
retical analysis and experimental results show that most
existing video watermarking methods [2-7] resisting to
C
opyright © 2012 SciRes. JIS

M. TONG ET AL. 139
geometric attack can resist cropping attacks with smaller
strength, but are sensitive to strong cropping attacks.
Nonnegative matrix factorization (NMF) is a matrix
factorization method under the condition that all the ele-
ments of the matrix are nonnegative, which can greatly
reduce the dimensions of the data. The decomposition
characteristics meet the experience of human visual per-
ception, and the decomposition results have interpretabil-
ity and clear physical meaning. Since it is proposed, N-
MF has been paid to great attentions, and it succeeds in
the application to pattern recognition, computer vision
and image engineering etc [8-11].
This paper proposes a new video watermarking scheme
based on nonnegative matrix factorization with sparseness
constraints on parts of the basis matrix (NMFSCPBM), in
which the watermark is embedded into the basis matrix
of NMFSCPBM. It uses video motion coefficients to
adaptively control the watermark embedding strength.
This scheme can resist various high-intensity cropping
attack, and experimental results show the effectiveness of
this scheme.
2. Complete Basis Matrix Recovery and
Video Motion Components Extraction
Based on NMFSCPBM
The NMF with sparseness constraints (NMFSC) method
is proposed in [12], which uses a nonlinear projection
operator to achieve the precise control of the sparseness
by adding sparseness constraints in all basis vectors. But
the data is described insufficiently under higher sparse-
ness constraints. A NMFSCPBM method is proposed in
this paper, in which controllable sparseness constraints
are added in the part of basis vectors. Not only can the
NMFSCPBM method extract video motion components
quickly and correctly, and filter out the static background
interference completely, but also solve the problems of
the NMFSC method under higher sparseness constraints.
Meanwhile it reduces the decomposition error and speeds
up the convergence rate.
2.1. NMFSCPBM Model Construction
Sparse matrix is the matrix that most of the elements are
zero or approach to zero and only a few are nonzero. The
sparse degree of a vector is defined as Equation (1).



2
1
ii
ny y
n


mn
r
 
2
, ij ij
ij
DBWHB WH




sparseness y  (1)
where n is the dimension of y [12].
So the NMFSCPBM can be transformed into the fol-
lowing constrained optimization problem that given a
nonnegative matrix B of size , solve the basis
matrix W of size and coefficient matrix H of
size , where r is the decomposition dimension of B.
If squared Euclidean distance D of primitive matrix and
reconstructed matrix is defined as the target evaluation
function, shown as Equation (2), which is used to de-
scribe the error between primitive matrix B and recon-
structed matrix WH, W and H should satisfy the condi-
tion of Equation (3).
m
rn
(2)



min , ,0,0
sparseness(), 1, 2, ,
ii
DBWH WH
wsi zzr







w
w


, 0
0,
ij ijjk
ik
k
ij ij
ij
ii
WW WHBH
WifW
Welse
wLw
   







 




(3)
where i is the ith column of the basis matrix I, and si is
the expected sparseness of .
i
The iteration rules of NMFSCPBM are described as
follows:
1) Basis matrix W:
(4)

where

Lw
w


i is performing nonlinear projection opera-
tion to [12].
i
2) Coefficient matrix H:
T
kj
kjkj T
kj
WB
HH
WWH

W
wWsparseness(, )ws
k
wk w
Wdw
(5)
Firstly, the definitions of some parameters used in it-
erative process are given. L is iterations. s is sparseness
degree. new is the sparse constraint matrix to be added.
k is the kth column of new . k is the
adding sparseness constraints with the sparseness degree
s for . is the column vector after the sparse con-
straint. newj is sparseness constraints matrix. is
intermediate variable,

is penalty factor.

is pen-
alty factor threshold.


is the convergence error thre-
shold of objective function. T is transpose operation.
Therefore, the iterative steps of NMFSCPBM can be
described below. The algorithm input is B, r, and L. The
output is W and H.
Step 1. Initialize

, set the loop variable I = 1, and
initialize W and H to random positive matrices.



Step 2.
T
T
WB
HH WWH 

,2 , DBWHB WH .


T
dwWHBH , Step 3. 12, .

1j
new
WW dw
Step 4. Add partly sparseness constraints to W and
start the iteration.
(a)



.

M. TONG ET AL.
JIS
140

, . kzzr

(b) .

sparseness, ,1,
kk
wws

(c)

2
newj
B WH, newj DBW H.
(d) If



H, , DBW
newj or DBW H

 , then
newj , turn to Step 5. Otherwise, return to Step 4(a),
and set
WW
2

 , . 1jj
Step 5. If 2 BWH
F


or i, then exit. Oth-
erwise, return to Step 2, and set .
L
1ii
H b

2.2. Complete Basis Matrix Recovery Based on
the Least Remaining Sub-Blocks
First of all, the definition of least remaining sub-blocks is
given, followed by the Theorem 1 and its proof, which is
the theoretical basis of resisting strong cropping attack of
this scheme. Here, the residual video is defined as the
remaining of the watermarked video after it is suffered
from cropping attacks.
The number of least remaining sub-blocks is defined
as the number of the least complete video sub-blocks
needed to recover the complete basis matrix from the
residual video.
Set the basic NMF modelmnmr rn . i is
the ith column of B. i is the ith column of H.
BW

h


12mn n and, , , bBbb


12rn , , , n
H
hh h
 are
substituted in the basic model of NMF, then:





12
, , ,
nmr
bbbW


12
, , ,
n
hh h

(6)
Outspread Equation (6), then Equation (7) is obtained.

1,
ri
hi n
aaK
im
bW

 (7)
Firstly, perform blocking preprocessing to video, shown
as Figure 1. The rules of blocking are as follows. Divide
original video V into sub-blocks with size of


along the temporal axis, and outspread each sub-block as
one column of nonnegative matrix B. Let
j
C


mod ()
2, 1, 2,,kK
2, , c
be the jth
sub-block of V, then:
directly set to 0, shown as Figure 2. Let c denote the
number of remaining complete sub-blocks after strong
cropping attacks. For convenience, the remaining com-
plete sub-blocks are rearranged from 1,


B
ac-
cording to blocking order. Then the data matrix

, the
coefficient matrix
H

and the base matrix W corre-
sponding to the remaining sub-blocks are as follows:
11 121
21 222
12
c
c
mm mc
bb b
bbb
B
bb b







See the Equation (8).
where denotes rounding operation toward 0,
denotes modulus operation, K is the number of
video frames, , and .
2
, iKa1,
Actually, cropping attacks may occur in anywhere of
the video. If video sub-blocks at its position suffer from
cropping attacks, the corresponding data in the data matrix








 

11 121
21 222
12
c
c
rr rc
hhh
hh h
H
hh h








 

11 121
21 222
12
r
r
mm mr
ww w
ww w
W
ww w
, ,














 

r
'BWH

, where is the dimension

of nonnegative matrix factorization. According to Equa-
tion (7), Equation (9) is obtained.
(9)


B
Equation (9) shows that after the video suffers strong
cropping attacks,

is obtained by Equation (8) and
'
H
and complete matrix W can be obtained by the
iteration rules of NMFSCPBM. Therefore, the following
Theorem 1 is established.
Theorem 1: When the watermarked video suffers
from strong cropping attacks, as long as the residual
video contains the number of least remaining sub-blocks
and meets, the complete basis matrix W can be
recovered from residual video uniquely and correctly.
cr
''
TT T
Theorem 1 is proved as follows. Transpose Equation
(9) to obtain Equation (10).
H
WB
B
(10)

, Take '
H
and W into Equation (10), then Equa-
tion (11) is obtained.
See the Equation (11).
Let ,,
, ,,
, , ,
then Equation (11) is converted into:

11112 1
T
r
wwww

22122 2
T
r
www w


12
T
mmmmr
wwww

111121
T
c
bbb b

22122 2
T
c
bbbb

12
T
mmm mc
bbb b
 


  
mod, ,1, mod, 0
,1, mod, 0
j
j
Ciaiaakkifia
Caiaa kkifia


(, )Bi j
 





 


11 2111121111 211
2221222212222
1 212
rmm
rmm
crcrrmrc cmc
hhhwwwbbb
h wwwbbb
h wwwbbb
 
 
 

 
 
 
 
 
 
 


(8)
12
12
c
hh
hh
 (11)

M. TONG ET AL. 141
1
2
K
a
aa
a
12



n v

B=
v
v
aaK

Frame number
Column Column Column Column
Figure 1. Video blocking of this paper.


12
,, ,,,
vn
b
B
bb b


1,,,0,,0,,,
s
vn
b

  
B
bb b
Original videoBlocking
Strong
cropping attacks


1,,,,,
s
vn


 
B
bbbb
Figure 2. Vide suffer from strong cropping.




12
'T
12mm
H
www bb b
'T
(12)
Let
A
H, then Equation (12) can be converted to
the following linear equations, shown as Equation (13),
where A is the coefficient matrix of each equations and


12 m
w w
11
22
mm
T
Ww is the unsolved unknown
vectors.
A
wb
A
wb
A
wb










 (13)
What follows is: taking the linear equation 11
A
wb

as example, the existence and uniqueness of its solution
is discussed. By the uniqueness of nonnegative matrix
decomposition results, we know that, 11
A
wb is solv-
able and has a unique solution. In fact, the necessary
and sufficient conditions of r-dimensional homogeneous
linear equations are


RA RA r, where


11
'T
A
Ab

H b


 
is the augmented matrix of A,
and

RA

RA are the rank of A and
A
respec-
tively, , and



min ,r

cRA

RA

min 1,rc
r
. It
can be divided into three cases. 1) If c

and


RA cRA r, 11
A
wb has infinite solutions;
2) If and cr


RARAr, 11
A
wb

has infi-
nite solutions. The above two cases violate to uniqueness
of the nonnegative matrix factorizing results, the solu-
tions are rejected. 3) If and
cr


RA rRA,
11
A
wb has the unique solution. Similarly, other equa-
tions have the same conclusions.
We can see from the above solution process, if cr



RA RA r, , ,
m
ww w
crW
and

, 12 separately has
unique solution, or the base matrix W has a unique
solution. In other words, when the watermarked video
suffers from strong cropping attacks, as long as the re-
sidual video contains complete video sub-blocks and the
number meets , the complete basis matrix can
be recovered from residual video uniquely and correctly.
Namely, Theorem 1 is established. Experimental results
of this paper verify the correctness of theoretical analysis.
2.3. Video Motion Components Extraction Based
on NMFSCPBM
The basis matrix and coefficient matrix can be obtained
by nonnegative matrix factorizing. Basis matrix repre-
sents the major features of video. Coefficient matrix is
the linear projection of nonnegative matrix to basis ma-
trix and represents the local feature weights of video.
Video frames can be seen as linear weighted sum of the
static components and motion components. In general,
the static components are nonsparse, while the motion
components are sparse. So motion component can be
separated from the static background by controlling
sparseness constrains of the basis matrix, and then extract
the motion components. The motion component extrac-
tion processes based on NMFSCPBM includes:
1) Video pre-processing. Take the target frame of the
movement components to be extracted as the center for
the original video


Vm mK
21
l
xy and choose the for-
ward and the next l frames separately. Let the total

.

frames compose of a video frame group V

Outspread V one-dimensionally as one column of non-

M. TONG ET AL.
142
negative mix B, shown as Equation (14), where the
size of video frame is
atr
x
y
mm

, 1, 2, ,
x
y
imm,
1, 2, , 21jl. The p-
chosen too large, calculation is risen
significantly. Ifl is chosen too small, there have no
obvious motion information between video frames.

arameter l needs a reason
able choice. If l is
 
, , mod, , Bi jVimimj


 xx
factorization. Perform
(14)
2) NMFSC NMFSCPBMPBM
to matrix B, and set r as the factorization dimension. Add
sparseness constraints to the


1r basis vectors, so the
basis vectors constrained spars

1,2, , 1
i
wi r
represents the motion components o
3) Solving Video motion components. Motio
eness
f video [12].
n com-
ponents
M
of target frame can be obtained by weight-
ing and mming to the

1r su

motion components,
shown as Equation (15).
1r
,1
1
iil
i
MwH



eighting coefficient o

,1 is the w
spon
(15)
il Hf basis vectors
e
where,
tar
i
w corrding to target frame. For each pixels of the
get frame, there is one element in
M
which is cor-
responding to it,
M
has the same size with target frame,
the bigger of the element in
M
, the more intensity of
the corresponding pixels movinn target frame.
Motion components extracted by the NMFS
g i
and other similar methods are shown in Figure 3. It can
be seen that, the motion components in Figure 3(b) ex-
tracted by the proposed method filter out the static back-
ground interference completely, and show the trajectory
clearly compared with Figure 3(a). Figure 3(c) cannot
distinguish the moving target from static background and
cannot show the trajectory. Figure 3(d) has improved a
little compared with Figure 3(c), but still cannot separate
the moving target from static background completely. To
quantitatively assessment the effectiveness of the motion
components extraction of this paper, the matching rate
[13] τ is defined to evaluate as follows:



CPBM
 
,
,,
,SMD,
,, SMD,SMD,
xy R
xy RxyR
Ixy xy
I xyIxyxyxy



 



(16)


SMD ,
x
y is the motion components extracted, where


,
I
xy
R
is the manually specified target motion area,
and is the target frame. The more the

is close to
1, the more matching of the extracted motion features
compared with the features specified motion area. When
the extracted motion features are exactly the same with
the features specified motion area, 1

.
The experiment chooses “hall”, “stefan” and “tennis”
as test videos. (http://trace.eas.asu.edu/yuv/index.html).
(a)
(b)
(c)
(d)
. ults obtained byFSCPBM method and other similar methods. (a) Original Figure 3Motion components extraction res NM
video; (b) Motion components extraction results obtained by NMFSCPBM; (c) Motion components extraction results ob-
tained by NMFSC; (d) Motion components extraction results obtained by NMF.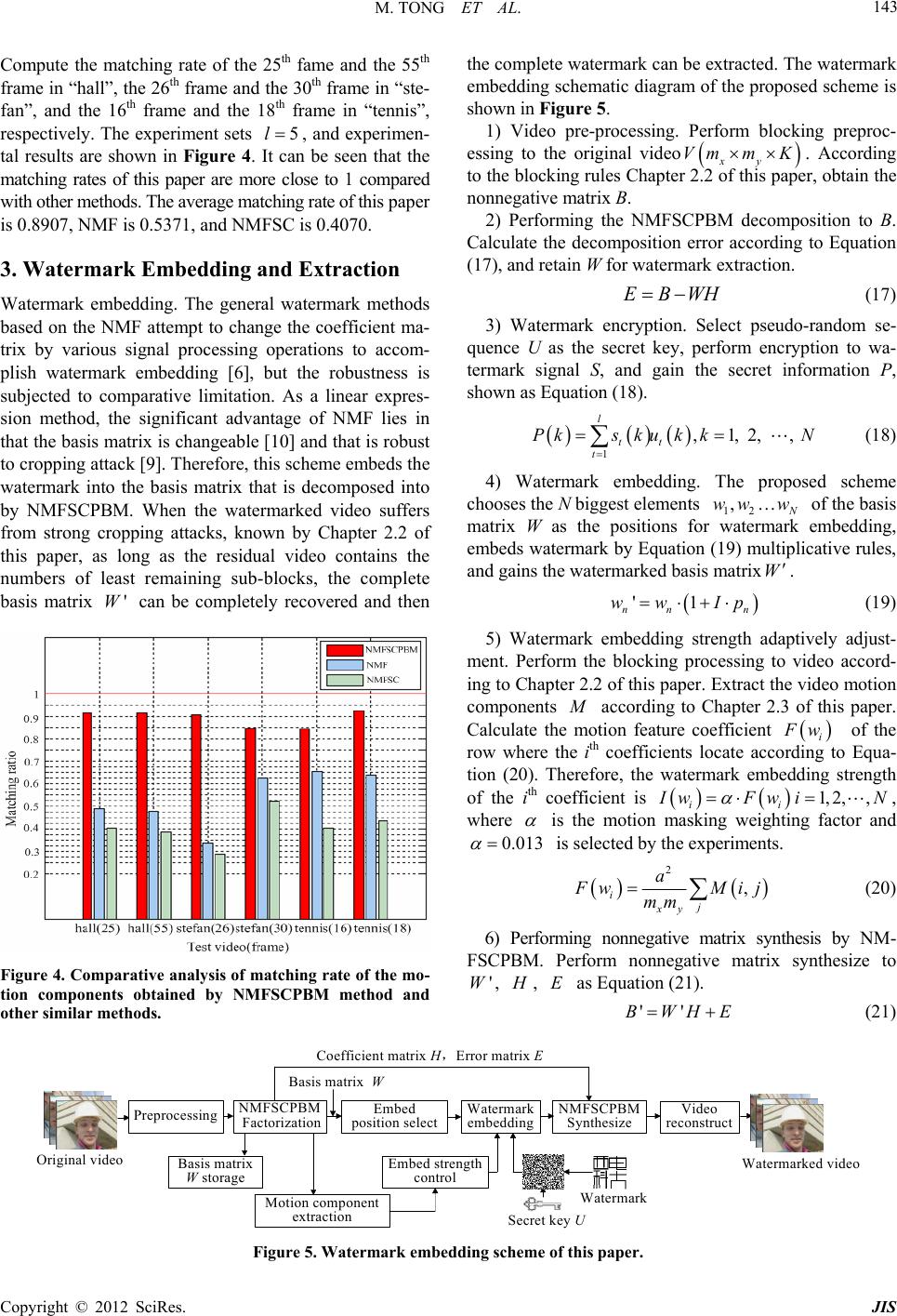

M. TONG ET AL. 143
ompute the matching rate of the 25th fame and the 55th C
frame in “hall”, the 26th frame and the 30th frame in “ste-
fan”, and the 16th frame and the 18th frame in “tennis”,
respectively. The experiment sets 5l, and experimen-
tal results are shown in Figure 4. It can be seen that the
matching rates of this paper are more close to 1 compared
with other methods. The average matching rate of this paper
is 0.8907, NMF is 0.5371, and NMFSC is 0.4070.
3. Watermark Embedding and Extraction
ds Watermark embedding. The general watermark metho
based on the NMF attempt to change the coefficient ma-
trix by various signal processing operations to accom-
plish watermark embedding [6], but the robustness is
subjected to comparative limitation. As a linear expres-
sion method, the significant advantage of NMF lies in
that the basis matrix is changeable [10] and that is robust
to cropping attack [9]. Therefore, this scheme embeds the
watermark into the basis matrix that is decomposed into
by NMFSCPBM. When the watermarked video suffers
from strong cropping attacks, known by Chapter 2.2 of
this paper, as long as the residual video contains the
numbers of least remaining sub-blocks, the complete
basis matrix 'W can be completely recovered and then
Figure 4. Comparative analysis of matching rate of the mo-
atermark can be extracted. The watermark
cessing. Perform blocking preproc-
es
2.2 of this pape
MFSCPBM decomposition to B.
C
tion components obtained by NMFSCPBM method and
other similar methods.
the complete w
embedding schematic diagram of the proposed scheme is
shown in Figure 5.
1) Video pre-pro
sing to the original video

xy
Vm mK . According
to the blocking rules Chapterr, obtain the
nonnegative matrix B.
2) Performing the N
alculate the decomposition error according to Equation
(17), and retain W for watermark extraction.
E
BWH

 (17)
3) Watermark encryption. Sel
qu

1
,1, 2, ,
tt
t
Pks kukkN

 (18)
4) Watermark embedding. The proposed scheme
ch
ect pseudo-random se-
ence U as the secret key, perform encryption to wa-
termark signal S, and gain the secret information P,
shown as Equation (18).
 
l

ooses the N biggest elements 12 ,
N
ww w of the basis
matrix W as the positions for embedding,
embeds watermark by Equation (19) multiplicative rules,
and gains the watermarked basis matrixW.

'1
nn n
ww Ip
watermark
(19)
5) Watermark embedding strength
m
adaptively adjust-
ent. Perform the blocking processing to video accord-
ing to Chapter 2.2 of this paper. Extract the video motion
components
M
according to Chapter 2.3 of this paper.
Calculate theotion feature coefficient

i
m
F
w of the
row where the ith coefficients locate according to Equa-
tion (20). Therefore, the watermark embedding strength
of the ith coefficient is


1, 2,,
ii
I
wFwi N  ,
where

is the motion d
0.0
masking weighting factor an
13


is selected by the experiments.
 
2
a
F
,
i
j
xy
wMij
mm
 (20)
6) Performing nonnegative matrix synthesis by NM-
FSCPBM. Perform nonnegative matrix synthesize to
'W,
H
, E as Equation (21).
''BWHE

 (21)
Basis matrixW
Coefficient matrix H，Error matrix E
NMFSCPBM
Factorization
NMFSCPBM
Synthesize

W
Secret key U
Watermark
Original viWatermarked video deo
Preprocessing Watermark
embedding
Video
reconstruct
Embed
position select
Basis matrix
W storage
Embed strength
control
Motion component
extraction
Figure 5. Watermark embedding sche me of this paper.

M. TONG ET AL.
144
7) Video reconstructiocon
lter
mark extraction. The watermark extraction sche-
m
sid
in
W
2),
1if ww (22)
4. Experiment and Analysis
is paper, the videos
4.1. Transparency Tests
frame video captures of
and after the watermark is em-
4.2. Bit Rate Constancy Tests
e bit rate constancy of
n. Restruct 'B according to of video coding before
b ocking rules, and then output the wamarked video
finally.
Water
atic diagram of the proposed scheme is shown in Fig-
ure 6. Firstly, perform the blocking preprocessing for the
watermarked video that has been attacked according to
Chapter 2.2 of this paper, obtaining the nonnegative ma-
trix B constituted by the remaining complete sub-blocks
in reual video. Secondly, perform the NMFSCPBM
decomposition toB, getting the watermarked complete
basis matrix 'W residual video. Finally, by compar-
ing W with ', the encrypted watermark is extracted
as Eation (2 and then it is decrypted by the secret
key U. From the process of watermark extraction, we
know that the watermark extraction of this scheme does
not need original video. So it is a blind watermark scheme.
0if ww 

qu
'
p

In order to verify the validity of th
“football”, “mother-daughter”, “tempete”, “mobile”, “aki-
yo”, “hall”, “foreman” and “soccer” with the format of
CIF and the length of 300, 260, 260, 300, 300, 300, 300
and 300 frames are selected as the host video for ex- pe-
riment respectively. A 64 × 64 binary image is selected
as the watermark, the size of sub-block is 8 × 8, the de-
composition dimension r of NMFSCPBM is 32, and the
experimental software environment is matlab 7.2. The
experiment conducts the test and analysis about the
transparency, bit rate constancy, robustness, real-time
property, and the algorithm efficiency etc. for this scheme
respectively. Due to the length limitation of this paper,
only a partial list of results are listed such as the transpar-
ency, bit rate constancy, and strong cropping attacks etc.
Figures 7(a) and (b) are the I-
the original frame and watermarked frame from football
sequence. It can be seen that there is no significant visual
perceptive distortion before and after the watermark is
embedded. From the quantization assessment data shown
in Tab le 1, we also know that the difference value ΔPSNR
bedded decreases only by average 0.025dB (PSNR, Peak
Signal to Noise Ratio of video coding) and that there is
no influence on visual perception. The reason is that the
proposed scheme sufficiently considers the visual mask-
ing features for watermark embedding position selection
and strength control, embeds the watermark into the big
coefficients of the basis matrix, and meanwhile embeds
comparatively strong strength watermark into the regions
where the motion is intense [14], eliminating the flicker
influence and guaranteeing the transparency of the method.
Table 2 shows the test results of th
this paper. The experiment is assessed by the bit in-
creased rate (BIR) before and after the watermark is em-
bedded, as Equation (23).
_
BIR watermarked B 
-_ 100 %
_
R originalBR
original BR (23)
where original_BR is the bit rate before the watermark is
4.3. Strong Cropping Attacks Experiments
nd ir-
embedded, and watermarked_BR is the bit rate after the
watermark is embedded. It can be seen that the increase
in video BIR after the watermark is embedded in this
paper is under 0.15%, with a good bit rate constancy.
Strong cropping attacks include various regular a
regular cropping, such as row and column cropping, edge
cropping, top right corner cropping and center cropping
etc. The same type and intensity of cropping attacks are
synchronously carried out to paper [3], and the compara-
tive analysis is given. The experimental results are as-
sessed by the bit correct rate (BCR) of the extracted wa-
termark, as Equation (24).
BCR 100%
m (24)
where e is the number of correct bits of the extracted
e

watermark, and m is the number of total bits of the ex-
tracted watermark. The more the BCR is close to 100%,
the more higher of the correct rate. Let the threshold
70.00%T

that is determined by experiments. If
he watermark is detected. Some figures and BCR >T , t
Basis
matrix W
W

Watermarked
video
Waterma rk
Secret key U
Strong
cropping attacks
Residual
video NMFSCPBM
Factorization
Preprocessing Nonnegative
Matrix B Watermark extraction
Figure 6. Watermark extraction scheme of this paper.

M. TONG ET AL. 145
(a) Original video and watermark (b) Watermarked video and extracted waterark(c) Left bottom cropping 95.01%, BCR = 100%m
(d) Column corpping 97.73%, BCR = 100% (e) Row and column cropping 97.98%, BCR=100%(f) Row cropping 97.22%, BCR = 100%
(g) Row and column cropping 97.98%, (h) Edge cropping 97.73%, BCR=100% (i) Row and column cropping 96.72%,
BCR = 100% BCR = 100%
(j) Irregular cropping 94.51%, BCR = 100% (k) Irregular cropping 95.04%, BCR = 100% (l) Irregular cropping 95.50%, BCR = 100%
(m) Irregular cropping 95.53%, BCR = 100% (n) Irregular cropping 96.17%, BCR = 100% (o)Irregular cropping 96.56%, BCR = 100%
. Sis p
Table 1. Transparency test results of this paper.
Figure 7trong cropping attacks test results of thaper.
Table 2. Bit rate constancy tests results of this paper.
PSNR (dB)
Test video Without wa watermark
△PSNR
termark With(dB)
football 33.25 33.24 0.01
motter
fo
her-daugh37.90 37.87 0.03
tempete 32.92 32.88 0.04
mobile 32.22 32.17 0.05
akiyo 38.45 38.44 0.01
hall 36.31 36.28 0.03
reman 35.15 35.14 0.01
soccer 34.31 34.29 0.02
Bit rate (kbps)
Test video watermarked_BR original_BR BIR
football 166768.89 0. .98 160546%
mo0.0720%
f
s
ther-daughter222.22 222.38
tempete 1101.06 1101.61 0.0500%
mobile [phone].0018%
akiyo 226.49 226.52 0.0130%
hall 415.98 416.05 0.0168%
oreman489.58 490.33 0.1500%
occer 654.55 655.44 0.1400%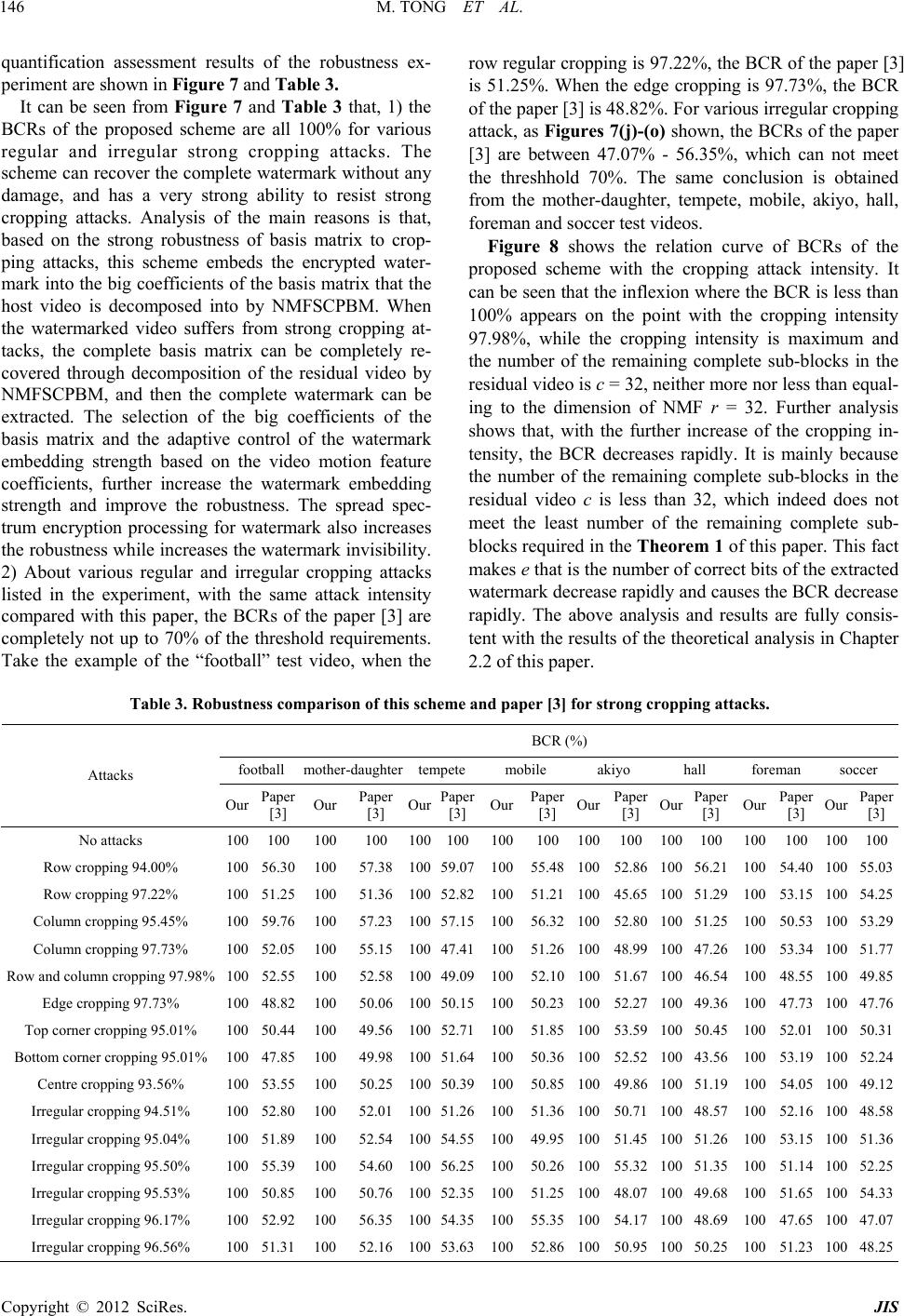

M. TONG ET AL.
146
quann assesslts oobu-
perime shown ie 7 and.
for various
curve of BCRs of the
pr
and paper [3] for strong cropping attacks.
tificatioment resuf the rstness ex
ent arn Figur Table 3
It can be seen from Figure 7 and Table 3 that, 1) the
BCRs of the proposed scheme are all 100%
regular and irregular strong cropping attacks. The
scheme can recover the complete watermark without any
damage, and has a very strong ability to resist strong
cropping attacks. Analysis of the main reasons is that,
based on the strong robustness of basis matrix to crop-
ping attacks, this scheme embeds the encrypted water-
mark into the big coefficients of the basis matrix that the
host video is decomposed into by NMFSCPBM. When
the watermarked video suffers from strong cropping at-
tacks, the complete basis matrix can be completely re-
covered through decomposition of the residual video by
NMFSCPBM, and then the complete watermark can be
extracted. The selection of the big coefficients of the
basis matrix and the adaptive control of the watermark
embedding strength based on the video motion feature
coefficients, further increase the watermark embedding
strength and improve the robustness. The spread spec-
trum encryption processing for watermark also increases
the robustness while increases the watermark invisibility.
2) About various regular and irregular cropping attacks
listed in the experiment, with the same attack intensity
compared with this paper, the BCRs of the paper [3] are
completely not up to 70% of the threshold requirements.
Take the example of the “football” test video, when the
row regular cropping is 97.22%, the BCR of the paper [3]
Table 3. Robustness comparison of this scheme
is 51.25%. When the edge cropping is 97.73%, the BCR
of the paper [3] is 48.82%. For various irregular cropping
attack, as Figures 7(j)-(o) shown, the BCRs of the paper
[3] are between 47.07% - 56.35%, which can not meet
the threshhold 70%. The same conclusion is obtained
from the mother-daughter, tempete, mobile, akiyo, hall,
foreman and soccer test videos.
Figure 8 shows the relation
oposed scheme with the cropping attack intensity. It
can be seen that the inflexion where the BCR is less than
100% appears on the point with the cropping intensity
97.98%, while the cropping intensity is maximum and
the number of the remaining complete sub-blocks in the
residual video is c = 32, neither more nor less than equal-
ing to the dimension of NMF r = 32. Further analysis
shows that, with the further increase of the cropping in-
tensity, the BCR decreases rapidly. It is mainly because
the number of the remaining complete sub-blocks in the
residual video c is less than 32, which indeed does not
meet the least number of the remaining complete sub-
blocks required in the Theorem 1 of this paper. This fact
makes e that is the number of correct bits of the extracted
watermark decrease rapidly and causes the BCR decrease
rapidly. The above analysis and results are fully consis-
tent with the results of the theoretical analysis in Chapter
2.2 of this paper.
BCR (%)
football mother-daughtertempetemobakiyo hall foreman soccer ile
Attacks
O OrOrOurOur er OrOr
ur Paper
[3] Our Paper [3] ur Pape [3]ur Pape [3] rPape [3]
Pap
[3] ur Pape [3] ur Pape [3]
No attacks 100 100 100 100 100100100100100100100 100 100 100 100100
Row 00%
C
Row8%
To
B
Irregular cropping 94.51%
cropping 94.100 56.30 100 57.3810059.0710055.4810052.86100 56.21 100 54.4010055.03
Row cropping 97.22% 100 51.25 100 51.3610052.8210051.2110045.65100 51.29 100 53.1510054.25
olumn cropping 95.45%100 59.76 100 57.2310057.1510056.3210052.80100 51.25 100 50.5310053.29
Column cropping 97.73% 100 52.05 100 55.1510047.4110051.2610048.99100 47.26 100 53.3410051.77
and column cropping 97.9100 52.55 100 52.5810049.0910052.1010051.67100 46.54 100 48.5510049.85
Edge cropping 97.73% 100 48.82 100 50.0610050.1510050.2310052.27100 49.36 100 47.7310047.76
p corner cropping 95.01%100 50.44 100 49.5610052.7110051.8510053.59100 50.45 100 52.01 100 50.31
ottom corner cropping 95.01%100 47.85 100 49.9810051.6410050.3610052.52100 43.56 100 53.1910052.24
Centre cropping 93.56% 100 53.55 100 50.2510050.3910050.8510049.86100 51.19 100 54.0510049.12
100 52.80 100 52.0110051.2610051.3610050.71100 48.57 100 52.16 10048.58
Irregular cropping 95.04% 100 51.89 100 52.5410054.5510049.9510051.45100 51.26 100 53.15 10051.36
Irregular cropping 95.50% 100 55.39 100 54.6010056.2510050.2610055.32100 51.35 100 51.14 10052.25
Irregular cropping 95.53% 100 50.85 100 50.7610052.3510051.2510048.07100 49.68 100 51.65 10054.33
Irregular cropping 96.17% 100 52.92 100 56.3510054.3510055.3510054.17100 48.69 100 47.65 10047.07
Irregular cropping 96.56% 100 51.31 100 52.1610053.6310052.8610050.95100 50.25 100 51.23 10048.25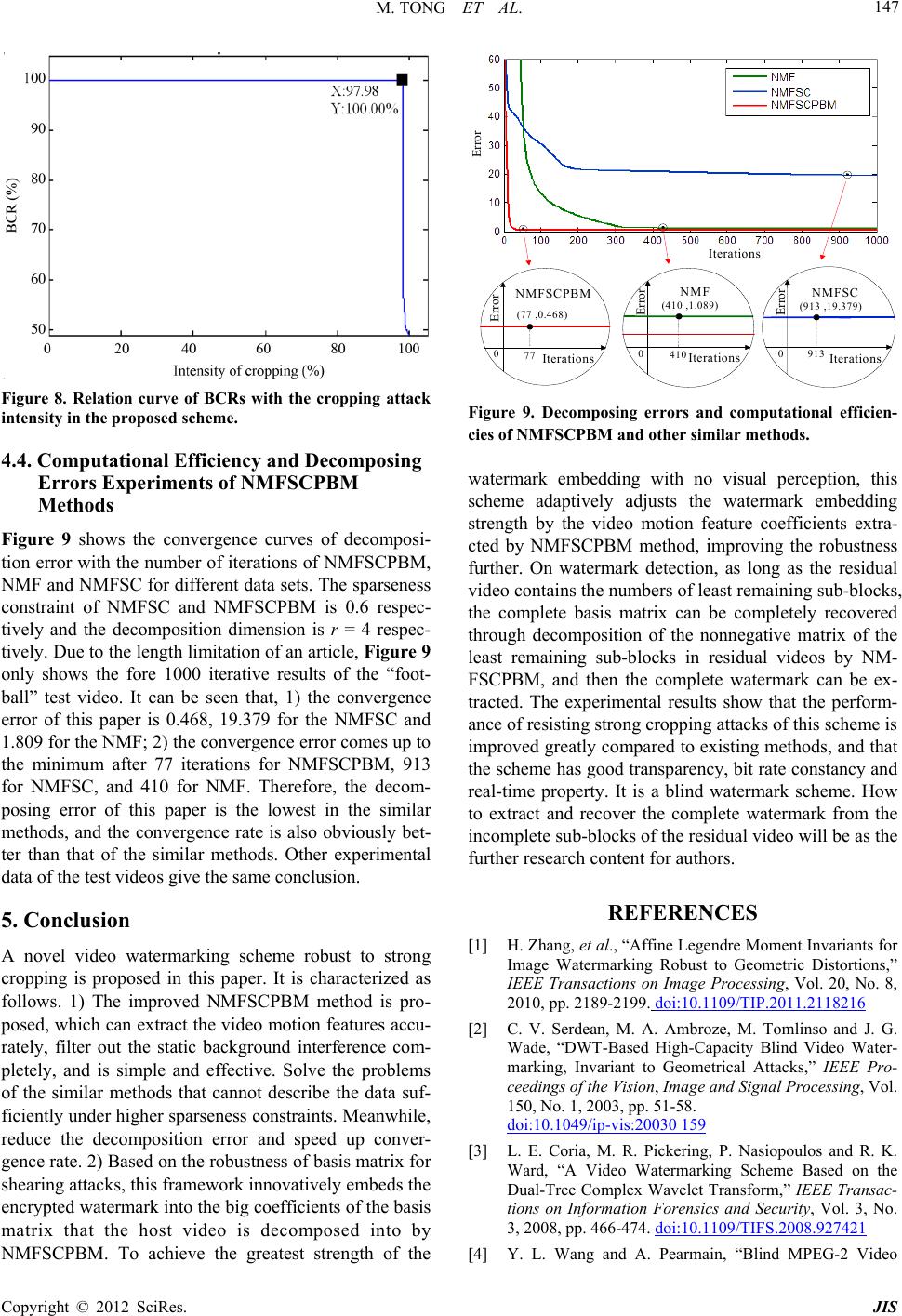

M. TONG ET AL. 147
Figure 8. Relation curve of BCRs with the cropping attack
intensity in the proposed scheme.
y and Decomposing
Figu he convergence curves of decomposi-
termarking scheme robust to strong
4.4. Computational Efficienc
Errors Experiments of NMFSCPBM
Methods
re 9 shows t
tion error with the number of iterations of NMFSCPBM,
NMF and NMFSC for different data sets. The sparseness
constraint of NMFSC and NMFSCPBM is 0.6 respec-
tively and the decomposition dimension is r = 4 respec-
tively. Due to the length limitation of an article, Figure 9
only shows the fore 1000 iterative results of the “foot-
ball” test video. It can be seen that, 1) the convergence
error of this paper is 0.468, 19.379 for the NMFSC and
1.809 for the NMF; 2) the convergence error comes up to
the minimum after 77 iterations for NMFSCPBM, 913
for NMFSC, and 410 for NMF. Therefore, the decom-
posing error of this paper is the lowest in the similar
methods, and the convergence rate is also obviously bet-
ter than that of the similar methods. Other experimental
data of the test videos give the same conclusion.
5. Conclusion
A novel video wa
cropping is proposed in this paper. It is characterized as
follows. 1) The improved NMFSCPBM method is pro-
posed, which can extract the video motion features accu-
rately, filter out the static background interference com-
pletely, and is simple and effective. Solve the problems
of the similar methods that cannot describe the data suf-
ficiently under higher sparseness constraints. Meanwhile,
reduce the decomposition error and speed up conver-
gence rate. 2) Based on the robustness of basis matrix for
shearing attacks, this framework innovatively embeds the
encrypted watermark into the big coefficients of the basis
matrix that the host video is decomposed into by
NMFSCPBM. To achieve the greatest strength of the
(77 ,0.468)
77
(410 ,1.089)
410
(913 ,19.379)
NMFSCPBM NMF NMFSC
913
Error
Iterations
000
Iterations
Error
Error
Iterations Iterations
Error
Figure 9. Decomposing errors and computational efficien-
cies of NMFSCPBM and other similar methods.
ents extra-
Moment Invariants for
Image Watermarking Robust to Geometric Distortions,”
IEEE Transacng, Vol. 20, No. 8,
2010, pp. 2189
watermark embedding with no visual perception, this
scheme adaptively adjusts the watermark embedding
strength by the video motion feature coeffici
cted by NMFSCPBM method, improving the robustness
further. On watermark detection, as long as the residual
video contains the numbers of least remaining sub-blocks,
the complete basis matrix can be completely recovered
through decomposition of the nonnegative matrix of the
least remaining sub-blocks in residual videos by NM-
FSCPBM, and then the complete watermark can be ex-
tracted. The experimental results show that the perform-
ance of resisting strong cropping attacks of this scheme is
improved greatly compared to existing methods, and that
the scheme has good transparency, bit rate constancy and
real-time property. It is a blind watermark scheme. How
to extract and recover the complete watermark from the
incomplete sub-blocks of the residual video will be as the
further research content for authors.
REFERENCES
[1] H. Zhang, et al., “Affine Legendre
tions on Image Processi
-2199. doi:10.1109/TIP.2011.2118216
ol.
[2] C. V. Serdean, M. A. Ambroze, M. Tomlinso and J. G.
Wade, “DWT-Based High-Capacity Blind Video Water-
marking, Invariant to Geometrical Attacks,” IEEE Pro-
ceedings of the Vision, Image and Signal Processing, V
150, No. 1, 2003, pp. 51-58.
doi:10.1049/ip-vis:20030 159
[3] L. E. Coria, M. R. Pickering, P. Nasiopoulos and R. K.
Ward, “A Video Watermarking Scheme Based on the
Dual-Tree Complex Wavelet
tions on Information Forensic
Transform,” IEEE Transac-
s and Security, Vol. 3, No.
3, 2008, pp. 466-474. doi:10.1109/TIFS.2008.927421
[4] Y. L. Wang and A. Pearmain, “Blind MPEG-2 Video

M. TONG ET AL.
148
Watermarking Robust against Geometric Attacks: A Set
of Approaches in DCT Domain,” IEEE Transactions on
Image Processing, Vol. 15, No. 6, 2006, pp. 1536-1543.
doi:10.1109/TIP.2006.873476
[5] X. M. Niu, et al., “A Video Watermarking against Geo-
metrical Distortions,” Chinese Journal of Electronics, Vol.
12, No. 4, 2003, pp. 548-552.
[6] M. Silja and K. Soman, “A Watermarking Algorithm
chnologies in Communica-
based on Contourlet Transform and Nonnegative Matrix
Factorization,” Proceedings of the International Confer-
ence on Advances in Recent Te
tion and Computing, Kottayam, 27-28 October 2009, pp.
279-281. doi:10.1109/ARTCom.2009.198
[7] A. D’Angelo, Z. P. Li and M. Barni, “A Full-Reference
Quality Metric for Geometrically Distorted Images,” IE-
EE Transactions on Image Processing, Vol. 19, No. 4, 2010,
pp. 867-881. doi:10.1109/TIP.2009.2035869
[8] Z. Y. Yang, et al., “Blind Spectral Unmixing Based on
Sparse Nonnegative Matrix Factorization,” IEEE Trans-
actions on Image Processing, Vol. 20, No. 4, 2011, pp.
1112-1125. doi:10.1109/TIP.2010.2081678
[9] M. Tong, T. Yan and H.-B. Ji, “Strong Anti-Robust Wa-
terMarking Algorithm,” Journal of Xidian University,
Vol. 36, No. 1, 2009, pp. 22-27.
[10] D. Gai, X. F. He, J. W. Han and T. S. Huang, “Graph
Regularized Nonnegative Matrix Factorization for Data
Representation,” IEEE Transactions on Pattern Analysis
and Machine Intelligence, Vol. 33, No. 1, 2011, pp. 1-13.
doi:10.1109/TPAMI.2010.231
[11] T. Gao and M.-Y. He, “Using Improved Nonnegative
Matrix Factorization with Projected Gradient for Sin-
s Constraints,” Journal of Machine Learning Re-
e Background Gen-
gle-Trial Feature Extraction,” Journal of Electronics &
Information Technology, Vol. 32, No. 5, 2010, pp. 1121-
1125.
[12] P. O. Hoyer, “Nonnegative Matrix Factorization with Sp-
arsenes
search, Vol. 5, 2004, pp. 1457-1469.
[13] T. K. Kim, et al., “Video Object Segmentation and Its Sa-
lient Motion Detection Using Adaptiv
eration,” Electronics Letters, Vol. 45, No. 11, 2009, p. 542.
[14] S.-W. Kim, K. R. Rao, S. Suthaharan and H.-K. Lee,
“Perceptually Tuned Robust Watermarking Scheme for
Digital Video Using Motion Entropy Masking,” Pro-
ceedings of the International Conference on Consumer
Electronics of the IEEE ICCE, Los Angeles, 22-24 June
1999, pp. 104-105. doi:10.1109/ICCE.1999.785187