Productivity Growth, Technological Progress, and Efficiency Change in Vietnamese Manufacturing Industries: A Stochastic Frontier Approach

doi:10.4236/ojs.2012.22028

Paper Menu >>

Journal Menu >>

Open Journal of Statistics, 2012, 2, 224-235

http://dx.doi.org/10.4236/ojs.2012.22028 Published Online April 2012 (http://www.SciRP.org/journal/ojs)

Productivity Growth, Technological Progress, and

Efficiency Change in Vietnamese Manufacturing

Industries: A Stochastic Frontier Approach*

Nguyen Khac Minh1, Pham Van Khanh2, Nguyen Thi Minh3, Nguyen Thi Phuong Anh4

1Faculty of Economics, Water Resources University, Hanoi, Vietnam

2Military Technical Academy, Hanoi, Vietnam

3National Economics University, Hanoi, Vietnam

4Hanoi University of Science and Technology, Hanoi, Vietnam

Email: khacminh@gmail.com, van_khanh1178@yahoo.com

Received February 3, 2012; revised March 8, 2012; accepted March 19, 2012

ABSTRACT

This study applies a stochastic frontier production approach to decompose the sources of total productivity (TFP)

growth into technical progress and changes in technical efficiency of 8057 firms in Vietnamese manufacturing indus-

tries during 2003-2007. Using both total manufacturing industry and sub-manufacturing industrial regressions, the

analysis focuses on the trend of technological progress (TP) and technical efficiency change (TEC), and the role of

productivity change in economic growth. According to the estimated results, the annual technical progress for the

manufacturing industry and sub-manufacturing industries are calculated directly from the estimated parameters of the

translog stochastic frontier production function by taking a partial derivative of output with respect to time t. The aver-

age technical changes in manufacturing industry and sub-man ufacturing industries are positive, with an average techni-

cal change about 5.2%, 5.8%, 5.4%, 11.8%, 4.6%, 4.1%, 7.3%, 4.8%, 4.8% and 4.8% for total sample, food products &

beverages, textile & wearing apparel, footwear, paper & products, industrial chemicals, rubber & plastic products, non-

metallic mineral, basic & fabricated metal and other sub-industries, respectively. Total TFP in the manufacturing sector

has grown at the annual rate of 0.052, although the rate of growth decreased continuously during the sample period. For

the sub-industry estimates during the sample period, TFP grew fastest in the footwear sub-industry, with annual average

growth rate of 11.8%, followed by the rubber & plastic products with a rate of 7.3%, and the food products & beverages

with a rate of 5.8% pe r ann um .

Keywords: Total Factor Productivity; Technical Efficiency Change; Technological Progress; Stochastic Frontier

Approach; Vietnamese Manufacturing Industry

1. Introduction

In the “Solow residual approach”, technical progress is

usually considered to be the unique source of TFP growth.

TFP growth can be defined as the residual of output

growth after the contribution of labor and capital inputs

and subtracted from total output growth . This appro ach is

based on the assumption that the economies are produc-

ing along the production possibility frontier with full

technical efficiency (it does not allow inefficiency).

The concept of the efficiency frontier has been used to

present inefficiencies.

A varies of methods have been used to measure effi-

ciency and decomposition total factor productivity (TFP)

into technical progress, changes in technical efficiency.

These methods differ to the assumptions on the outer

bound of the frontier, which deterministic or stochastic

frontier production function, and to the method of meas-

urement parametric or non-parametric.

For nonparametric method, such as data envelopment

analysis (DEA). This method cannot separate deviation

from the frontier technology into their systematic and

random components. However, this method has the ad-

vantage of imposing no restrictions on the underlying

technology and have an advantage in dealing with disag-

gregated inpu ts and multiple output technologies.

An alternative method is called a stochastic frontier

production function approach. The most important dif-

ference between the stochastic frontier production func-

tion approach and the Solow residual approach to pro-

ductivity growth analysis lies in one assumption that

firms do not fully utilize existing technology since vari-

*The third author was supported by the National Foundation for Science

Technology Development, Vietnam (NAFOSTED), No. II6.2-2010.07.

N. K. MINH ET AL. 225

ous factors that lead to inevitable technical inefficiencies

in production.

The stochastic frontier production function approach

allows decomposing TFP into efficiency change (TE)

and technical progress (TP). From a policy perspective,

the decomposition of TFP into efficiency changes and

technical changes provides useful information in produc-

tivity analysis.

Since Nishimizu and Page [1] first proposed the de-

composition of TFP into efficiency changes and technical

changes, researchers have applied this approach to vari-

ous datasets in order to investigate productivity growth.

Bauer [2] estimated a translog cost frontier using da ta on

the US airline industry to decompose TFP growth into

efficiency, technical progress, and scale components.

Sangho Kim and Gwangho Han [3] applied a stochastic

frontier production model to Korean manufacturing in-

dustries to decompose the sources of total productivity

(TFP) growth into technical progress, changes in techni-

cal efficiency, and changes in allocative efficiency, and

scale effects. Empirical results based on data from 1980-

1994 showed that produ ctivity growth was driven mainly

by technical progress, that changes in technical effi-

ciency had a significant positive effect, and that alloca-

tive efficiency had a negative effect. They suggested that

specific guidelines are required to promote productivity

in each industry, and provided additional insights into

understanding the recent debate about TFP growth in

Korean manufacturing.

Hailin Liao et al. [4] applied a stochastic frontier ap-

proach to sector-level data within manufacturing and

examined total factor productivity (TFP) growth for eight

East Asian economies during 1963-1998, using both sin-

gle country and cross-country regression. The analysis

focuses on the trend of technological progress (TP) and

technical efficiency change (TEC), and the role of pro-

ductivity change in economic growth. The empirical re-

sults reveal that although input factor accumulation is

still the main source for East Asian economies’ growth,

TFP growth is accounting for an increasing and impor-

tant proportion of output growth, among which the im-

proved TEC plays a crucial role in productivity growth.

Nguyen Khac Minh et al. [5] applied a non-parametric

approach method to decompose the sources of total pro-

ductivity (TFP) growth of three sectors of Vietnamese

economy into technical progress and changes in technical

efficiency.

This study develops the study of Nguyen Khac Minh

et al. [6] “A decomposition of total factor productivity

growth in Vietnamese industries—a stochastic frontier

approach” to decompose TFP growth in Vietnamese

manufacturing industries from 2003-2007. We attempt to

decompose TFP growth in Vietnamese manufacturing

using a stochastic frontier production model, and provide

additional insights into understanding on TFP growth of

Vietnamese sub-manufacturing industries.

This paper is organized as follows. Section 2 presents

a decomposition of TFP and presents the functiona l form

of the estimation model. Section 3 discusses the data and

estimation results. Section 4 contains the conclusions.

2. Decomposition and Functional Form

2.1. Decomposition of TFP

A stochastic frontier production function can be defined





,exp

it itit

fxt u



1, ,iN

(1)

where it is the output of the ith firm in

the tth time perio d





1, ,tT



;

 is the production

frontier;



is an input vector, t is a time trend index

that serves as a proxy for technical change; and u (non-

negative) is the outpu t-oriented technical inefficiency.



Taking total differentials xt with respect to

time to get









dln,ln,ln,

fxt fxtfxt

tt xt















(2)

whereas the first and second terms on the right-hand side

are the output elasticit y of fron tier out put with resp ect to

time, defined as TP, the second term measures the input

growth weighted by output elasticities with respect to

input , ln ln





. A dot over a variable in-

dicates its rate change.

The derivative of the logarithm of (1) with respect to

time t and using (3) is gi ven by:

TP d



 





(3)

from Equation (3), TFP growth can be defined technical

change (TP) and technical efficiency change.

2.2. Model Specification

In our empirical study, we employ the stochastic frontier

approach. The output of the manufacturing industry (or

sub-industries) is assumed to be a function of two inputs,

namely capital and labor. The components of productiv-

ity change can be estimated within a stochastic frontier

approach, and the time-varying production frontier can

be specified in translog form as:

ln ln

lnln

ln, ,,

itojjit t

jl litjittt

tjjt itit

yxt

txv ujlLK

 





 











(4)

N. K. MINH ET AL.

226

In Equation (4), it is the observed output, t is the

time variable and x variab les are inpu ts, subscrip ts j an d l

index inputs. The efficiency error, u, accounting for pro-

duction loss due to un it-specific technical inefficiency, is

always greater than or equal to zero and assumed to be

independent of the random error, v, which is assumed to

have the usual properties . Equation (4)

can be rewritten as the following form:



~ 0,

iid N



1) Specification model for whole manufacturing in-

dustry



 



ln lnln

lnlnln

ln2

jjj

itL it KitLL

KKitLK itit

tKittttit it

LnyL K2

tL it

Ktttv u

 





 











where

is the firm’s output. The subscripts i repre-

sent the ith firm for . N is equal to 8057

for the total sample. t represents year for

and so T is equal to 5. The subscripts j represent the jth

industry for,

1,2,,iN

1, 2,,tT

, 1,2,jH

and

L represent ca-

pital and labor, respectively. The



 and





are un-

known parameters to be estimated.

2) Specification model for each industry



 



lnln2

lnlnln

itL it KitLL

KKitLK itit

tKittttit it

LnyL K2

tL it

Kt ttvu

 





 













(5)

The distribution of technical inefficiency effects, it,

is taken to be the non-negative truncation of the normal

distribution





, following Battese & Coelli [7],

to take the form as







T



tiex

itt ii

uuupt



,



 (6)

Here, the unknown parameter



represents the rate

of change in technical inefficiency, and the non-negative

random variable ui, is the technical inefficiency effect for

the ith firm in the last year for the data set. That is, the

technical inefficiency effects in earlier periods are a de-

terministic exponential function of the inefficiency ef-

fects for the corresponding forms in the final period (i.e.)

iTi given that data for the ith firm are available in

period t).

uu







is the set of T time periods. A firm with

a positive



is likely to improve its level of efficiency

over time and vice-verse. A value of 0







TE exp

it it

u

implies no

time-effect.

Since the estimates of technical efficiency are sensitive

to the choice of distribution assumptions, we consider

truncated normal distribution for general specifications

for one-sided error , and half-normal distribution can

be tested by LR test.

Given the estimates of parameters in Equations (5) and

(6), the technical efficiency level of a firm at time t is

defined as

(7)

and TEC is the change in TE, and the rate of technical

progress is defined by,





 

TPln ln

it t

itttttLitKi

fx LK

 









(8)

If technical change is non-neutral then this technical

change may vary for different input vectors. Hence, we

use the geometric mean between adjacent periods as a

proxy,



,1, 1

ln ln

TP 111

it jit t

fx fx















 











TEit TPit

(9)

Both and vary over time and across the

firms.

The output elasticities of input K and L are

ln ln ln

KKKKLKt

LL KLLLLt











 



 



The above equations indicate the percentage change in

output due to a 1% change in inputs. They can be used to

obtain an estimate of aggregate return to scale. The elas-

ticity of scale is defined as : e



.

The elasticity of scale (e) measures how output varies

as a particular input bundle is augmented by a scalar. If

the scale elasticity is unity, then the technology exhibits

constant returns to scale.

3. Data and Empirical Results

3.1. Data Issues

The panel data of Vietnamese manufacturing sectors’

annual time-series during 2003-2007 are used in esti-

mating production functions. The sectors and their SIC

classification numbers are listed in Table 1.

The sample consists of 8057 firms in Vietnamese

manufacturing industries. Data for these firms have been

taken for 5 years from 2003 to 2007. All these firms that

are selected at least 5 workers.

The basic data for the analysis have been drawn the

Database, 2007 version from General Statistics Office

(GSO). It contains information for about characterized

enterprises. The coverage includes public, private, and

N. K. MINH ET AL. 227

Table 1. Manufacturing sectors.

1) Manufacturing sector (Total

sample) 6) Industrial chemicals

2) Food products an d beverages 7) Rubber and plastic products

3) Textile and wearing apparel 8) Non-metallic mineral

4) Footwear 9) Basic & fabricated metal

products

5) Paper & products 10) Other manuf act uring industries

joint sector companies. The coverage of this database is

total manufacturing firms that existed from 2003 to 2007

with number of workers greater than 5.

The available Information includes data from the en-

terprises’ profit, balance sheets. Key variables on which

data were collected for this study include gross fixed

assets, wages, revenue, gr oss out put a n d fo re ign eq uity .

3.2. Variables for the Estimation of the Model

As discussed above, a two-input production function

framework is used to estimate technical efficiency. This

requires, for each firm, data on output, labor input and

capital input.

Deflated revenue has been taken as the measure of

output. For this purpose, the products of each enterprise

were matched with the wholesale price indices classifica-

tion, and the best available price series was chosen for

deflation.

Total number of employees connected to the produc-

tion has been taken as the measure of labor input for each

firm in our sample.

Gross fixed capital stock at constant prices (at year

2000) has been taken as the measure of capital input.

4. Empirical Results

The estimation of parameters in the stochastic frontier

mode given by Equations (8) and (9) are carried out via

maximum-likelihood method, using the program FRON-

TIER 4.1. Two kinds of panel are constructed. Individual

sub-Industry panel is used in the single regression, con-

sisting of total sample and 9 sub-manufacturing sectors

and 5 years’ observations; panel data is used in the re-

gression. Instead of directly estimating 2



and 2



FRONTIER 4.1 seeks estimates of





, 222







v v

(10)

which are also reported in the result table. These are as-

sociated with the variances of the stochastic term in the

production function, it and the inefficiency term it .

The parameter



must lie between zero and one. If the

hypothesis 0



 is accepted, this would indicate that



is zero and thus the efficiency error term,

should be remove from the model, leaving a specification

with parameters that can be consistently estimated by

OLS. Conversely, if the value of



is one, we have the

full-frontier model, where the stochastic term is not pre-

sent in the model.

4.1. Hypotheses Tests and Preferred Model

Chosen

We performed a number of LR test to identify the ade-

quate functional form and presence of inefficiency. We

examine various hypotheses, such as non-presence of

technical inefficiency effects, which can be tested by

using the generalized likelihood ratio statistics



, given

by:













2ln lnLH LH













where L(H0) is the value of the likelihood function for

the frontier model in which the parameter restrictions

specified by the null hypothesis H0 are imposed and L(H1)

is the value of the likelihood function for the general

frontier model. If the null hypothesis is true, then



has

approximately a mixed Chi-Squared distribution with

degrees of freedom equal to the difference between the

numbers of parameters estimated under H1 and H0, res-

pectively.

4.2. Hypotheses Tests for Aggregated Samples

Table 2 presents the test results of various null hypothe-

ses on the total sample.

1) The first null hypothesis that the technology in

Vietnamese manufacturing is a Cobb-Douglas





:0H

 

oLL KKKL tt



, is rejected for the total

sample and all aggregated-samples. Thus, the Cobb-

Douglas production function is not an adequate specifi-

cation for the Vietnamese manufacturing sector, given

the assumptions of the translog stochastic frontier pro-

duction function model, implying that the translog pro-

duction function better describes the technology for

Vietnamese manufacturing industries.

2) The second null hypothesis, that there is no techni-

cal change





:0H

 

o ttKtLtt



 is strongly

rejected by the data in all cases. It implies that the exis-

tence of technical progress, given the specified produc-

tion model.

3) The third null hypothesis, that technical progress is

neutral





:0H



otK tL.



Not that the translog parameterization of this stochas-

tic frontier model allows for non-neutral TP. TP is neu-

tral if all tj



s are equal to zero. Total sample, food &

beverages, footwear, paper & products, Industrial chemi-

cals, non-metallic mineral, basic & fabricated metal and

ther manufacturing industries cannot reject the hypothe- o

N. K. MINH ET AL.

228

Table 2. Generalized likelihood ratio of hypotheses for parameters of the SFPF for Vietname se manufac turing industries.

Hypothesis Log-likelihood value Test statistics Critical value Decision

1% 5%

Cobb-Douglas production function, H0: all



s are equal to zero (df = 6)

Total sample –48319.83 21475.94 16.81 12.59 reject

Food products & be verages –7559.98 31.65 16.81 12.59 reject

Textile & wearing apparel –4781.91 41.92 16.81 12.59 reject

Footwear –1007.15 29.69 16.81 12.59 reject

Paper & products –2731.46 25.00 16.81 12.59 reject

Industrial chemicals –1604.32 21.13 16.81 12.59 reject

Rubber & plastic products –2238.63 50.15 16.81 12.59 reject

Non-metallic mineral –3394.03 107.98 16.81 12.59 reject

Basic & fabricated me tal –10757.17 94.99 16.81 12.59 reject

Others –9754.55 86.46 16.81 12.59 reject

No technical change, 0



ttLtKtt

 





0:0

tL tK



(df = 4)

Total samp le –38319.59 1475.40 13.28 9.49 reject

Food products & beverages –7700.38 312.45 13.28 9.49 reject

Textile & wearing apparel –4871.20 220.51 13.28 9.49 reject

Footwear –1038.66 92.71 13.28 9.49 reject

Paper & products –2786.94 135.95 13.28 9.49 reject

Industrial chemicals –1622.30 57.08 13.2 8 9.49 reject

Rubber & plastic products –2339.36 51.61 13.28 9.49 reject

Non-metallic mineral –3408.05 136.03 13.28 9.49 reject

Basic & fabrica ted metal –10900.30 381.25 13.28 9.49 reject

Others –9871.85 32.06 13.28 9.49 reject

Neutral technical progress :



0:0



(df = 2)

Total sample –37582.35 0.99 9.21 5.99 accept

Food products & beverages –7551.48 14.65 9.21 5.99 reject

Textile & wearing apparel –4765.83 9.77 9.21 5.99 reject

Footwear –992.42 0.23 9.21 5.99 accept

Paper & products –2719.95 1.98 9.21 5.99 accept

Industrial chemicals –1595.48 3.44 9.21 5.99 accept

Rubber & plastic products –2216.81 6.49 9.21 5.99 reject at 5%

Non-metallic mineral –3340.88 1.68 9.21 5.99 accept

Basic & fabricated metal –10709.84 0.33 9.21 5.99 accept

Others –9712.29 1.93 9.21 5.99 accept

No technical inefficiency, H



 (df = 3)

Total sample –48321.28 21477.8 4 10.501 7 .045 reject

Food products & beverages –9464.15 3839.99 10.501 7.045 reject

Textile & wearing apparel –5977.24 2432.59 10.501 7.045 reject

Footwear –1277.32 569.79 10.501 7.045 reject

Paper & products –3658.84 1877.77 10.501 7.045 reject

Industrial chemicals –2113.51 1036.06 10.501 7.045 reject

Rubber & plastic products –3076.49 1725.86 10.501 7.045 reject

Non-metallic mineral –4358.00 2035.93 10.501 7.045 reject

N. K. MINH ET AL. 229

Continued

Basic & fabrica ted metal –13321.73 5223.78 10.501 7.045 reject

Others –12002.09 4579.61 10.501 7.045 reject

Half-normal distribution of technical inefficiency, 0:0H





(df = 1)

Total sampl e –37582.35 837.03 6.63 3.84 reject

Food products & beverages –7544.15 96.11 6.63 3.84 reject

Textile & wearing apparel –4760.95 169.35 6.63 3.84 reject

Footwear –992.42 32.43 6.63 3.84 reject

Paper & products –2719.95 91.22 6.63 3.84 reject

Industrial chemicals –1595.48 12.31 6.63 3.84 reject

Rubber & plastic products –2213.56 25.55 6.63 3.84 reject

Non-metallic mineral –3340.88 162.24 6.63 3.84 reject

Basic & fabrica ted metal –10709.84 191.64 6.63 3.84 reject

Others –9712.29 229.34 6.63 3.84 reject

Time invariant technical inefficiency, 0:0H





(df = 1)

Total samp le –37115.2 97.27 6.63 3.84 reject

Food products & beverages –7496.09 12.46 6.63 3.84 reject

Textile & wearing apparel –4676.28 32 6.63 3.84 reject

Footwear –976.21 33.96 6.63 3.84 reject

Paper & products –2674.30 32.97 6.63 3.84 reject

Industrial chemicals –1589.31 0.16 6.63 3.84 accept

Rubber & plastic products –2199.78 43.45 6.63 3.84 reject

Non-metallic mineral –3258.92 4.01 6.63 3.84 reject at 5%

Basic & fabricated metal –10614.02 21.32 6.63 3.84 reject

Others –9597.62 8.81 6.63 3.84 reject

The critical value for this test involving γ = 0 is obtained fr om Table 1 of Kodde and Palm (1986).

sis. Then, the existence of neutral technical progress in

the data set of these industries. In the case of food prod-

ucts & beverages, textile & wearing apparel and rubber

& plastic products, the hypothesis is rejected it implies

that the existence of non-neutral technical progress in the

data set of these industries.

4) Given the specification of stochastic frontier model,

there is a particular interest in testing the hypothesis of

the non-existence of sector-level inefficiency, expressed

by 0:0H







:0H





The first null hypothesis is str-

ongly rejected at the 1% significance level for all sam-

ples, suggesting that the average production function is

an inadequate representation of the aggregated models

for all cases and will underestimate the actual frontier

because of the manufacturing sector for all cases and will

underestimate the actual frontier because of the existence

of technical inefficiency effects.

5) The fifth null hypothesis, specifying that technical

inefficiency effects have half-normal distribution

0 against truncated normal distribution, is

rejected at the 1% significance level for the total sample

and all sub-samples.

6) The last null hypothesis, that technical inefficiency

is time-invariant





:0H





is rejected for total sam-

ple, food products and beverages, textile and wearing

apparel, footwear, paper & products, rubber and plastic

products, non-metallic mineral, basic & Fabricated metal

products and Other manufacturing industries at least the

5% significance level. The industrial chemicals are only

the case that cannot reject the hypothesis.

4.3. Estimation of Stochastic Production

Functions

Given the specifications of translog frontier with time-

varying inefficiency effects the results of statistical tests

of the estimated parameters, the preferred frontier models

are chosen and the estimates of their parameters are

given in Tables 3 and 4.

To estimate production frontier for the total sample

and aggregated samples, the maximum—likelihood es-

timates of the parameters in the translog stochastic fron-

tier production function, defined by Equations (4) and (5),

are employed in this study.

Moreover, since there may exist some uncontrollable

N. K. MINH ET AL.

230

Table 3. Panel estimation of stochastic frontier production and technical inefficiency model.

Total sample Food Textiles Footwear Paper

Variable Coefficient Coefficient Coefficient Coefficient Coefficient

Const t



2.928***

(0.076) 2.2214***

(0.171) 3.6363***

(0.250) 3.272***

(0.477) 4.1904***

(0.256)

lnK



0.497***

(0.019) 0.659***

(0.042) 0.5172***

(0.059) 0.403***

(0.124) 0.3306***

(0.070)

lnL



0.555***

(0.022) 0.4891***

(0.056) 0.3559***

(0.059) 0.526***

(0.117) 0.4411***

(0.091)

T t



0.13***

(0.01) 0.0968***

(0.029) –0.017***

(0.038) 0.047

(0.062) 0.0816

(0.025)***

tlnK



0.0092**

(0.004) 0.0088**

(0.004)

tlnL tL



–0.017***

(0.005) 0.0055

(0.004)

lnKlnL



–0.01***

(0.004) 0.0099

(0.011) –0.0219**

(0.009) –0.086***

(0.024) 0.0011

(0.021)

lnK2



0.005***

(0.002) –0.0214**

(0.005) 0.0008

(0.005) 0.033**

(0.013) 0.0055

(0.008)

lnL2



0.005

(0.003) 0.0154

(0.009) 0.0364***

(0.007) 0.066***

(0.016) 0.0226

(0.017)

t2 tt



–0.017***

(0.001) –0.0198***

(0.004) –0.0133***

(0.004) –0.015*

(0.008) –0.0144***

(0.004)



2 0.71***

(0.014) 0.7608***

(0.034) 0.6756***

(0.037) 0.465***

(0.045) 0.4413***

(0.028)



0.676***

(0.006) 0.6524

(0.018)*** 0.6782

(0.012)*** 0.578

(0.042)*** 0.6434

(0.021)***



1.254

(0.032) *** 1.155***

(0.086) 1.3537***

(0.061) 1.003***

(0.14) 1.0657***

(0.067)



0.027***

(0.003) 0.0254***

(0.007) 0.0426***

(0.008) 0.103***

(0.018) 0.0493***

(0.008)

log-likelihood function –37111.57 –7489.87 –4660.92 –959.229 –2657.86

Source: Authors’ estimates from the data source; Note: 1) standard errors are given in the parenthesis; 2) */**/***Denotes statically significant at the 10, 5 and 1

per cent levels, respectively.

stochastic shocks, such as changes of government poli-

cies or other conditions affecting firms’ production effi-

ciency, a stochastic frontier production approach is ap-

plied. Concerning productivity, there are two indices to

indicate whether firms in Vietnamese manufacturing

industry have a high or low production efficiency: 2



represents total variance of output, containing a random

error term v





and a technical inefficiency term







. However large value of 2



does not necessary

mean a less efficient way of production since it includes

two types of production variation.

The estimates of



are positive (or at least zero) in

the cases, except for the non-metallic mineral sub-indus-

try.

Almost coefficients of variables in all equations are

statistically significant. A significant



along with a

positive and significant



implies the existence of tech-

nical inefficiency that declines over the years, except for

the Industry Non-metallic Mineral.

Table 5 presents the average technical efficiency (TE)

for Vietnamese manufacturing industries for time period

during 2003-2007. Estimates of TE vary considerably,

both across manufacturing industries, and cross time pe-

riods. The average TE is 0.309 for the total sample. The

industrial chemical and rubber and plastics industries

have the highest and second highest estimates, 0.417 and

3.91, respectively. and the textile & wearing apparel and

non-metal mineral industries have the lowest and second

lowest estimates, 0.267 and 0.290, respectively. The

other industries have estimates the range from 0.300 to

0.342.

The average TE for all industries improves throughout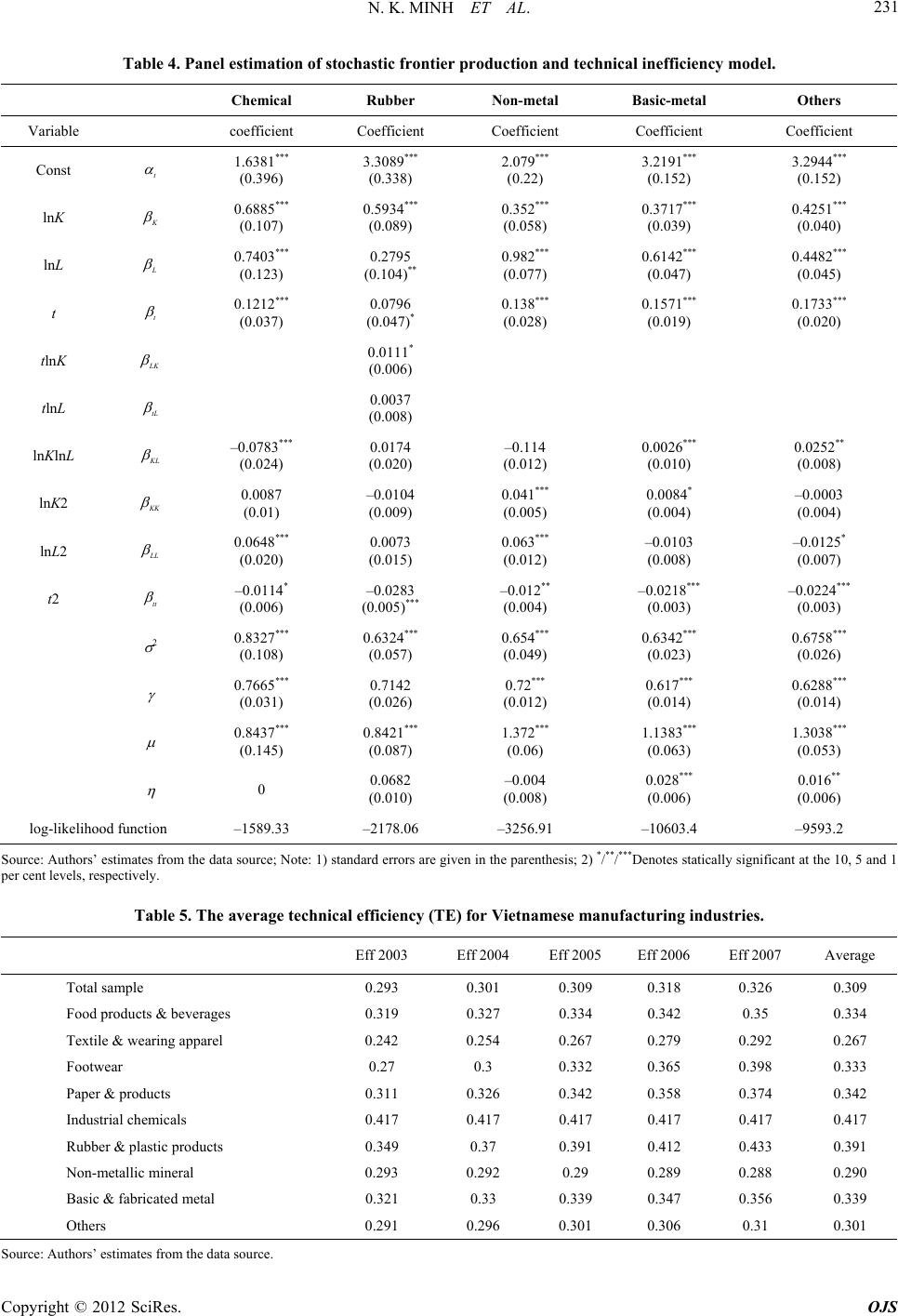

N. K. MINH ET AL. 231

Table 4. Panel estimation of stochastic frontier production and technical inefficiency model.

Chemical Rubber Non-metal Basic-metal Others

Variable coefficient Coefficient Coefficient Coefficient Coefficient

Const t



1.6381***

(0.396) 3.3089***

(0.338) 2.079***

(0.22) 3.2191***

(0.152) 3.2944***

(0.152)

lnK



0.6885***

(0.107) 0.5934***

(0.089) 0.352***

(0.058) 0.3717***

(0.039) 0.4251***

(0.040)

lnL



0.7403***

(0.123) 0.2795

(0.104)** 0.982***

(0.077) 0.6142***

(0.047) 0.4482***

(0.045)

t t



0.1212***

(0.037) 0.0796

(0.047)* 0.138***

(0.028) 0.1571***

(0.019) 0.1733***

(0.020)

tlnK



0.0111*

(0.006)

tlnL tL



0.0037

(0.008)

lnKlnL



–0.0783***

(0.024) 0.0174

(0.020) –0.114

(0.012) 0.0026***

(0.010) 0.0252**

(0.008)

lnK2



0.0087

(0.01) –0.0104

(0.009) 0.041***

(0.005) 0.0084*

(0.004) –0.0003

(0.004)

lnL2



0.0648***

(0.020) 0.0073

(0.015) 0.063***

(0.012) –0.0103

(0.008) –0.0125*

(0.007)

t2 tt



–0.0114*

(0.006) –0.0283

(0.005)*** –0.012**

(0.004) –0.0218***

(0.003) –0.0224***

(0.003)



2 0.8327***

(0.108) 0.6324***

(0.057) 0.654***

(0.049) 0.6342***

(0.023) 0.6758***

(0.026)



0.7665***

(0.031) 0.7142

(0.026) 0.72***

(0.012) 0.617***

(0.014) 0.6288***

(0.014)



0.8437***

(0.145) 0.8421***

(0.087) 1.372***

(0.06) 1.1383***

(0.063) 1.3038***

(0.053)



0 0.0682

(0.010) –0.004

(0.008) 0.028***

(0.006) 0.016**

(0.006)

log-likelihood function –1589.33 –2178.06 –3256.91 –10603.4 –959 3 .2

Source: Authors’ estimates from the data source; Note: 1) standard errors are given in the parenthesis; 2) */**/***Denotes statically significant at the 10, 5 and 1

per cent levels, respectively.

Table 5. The average technical efficiency (TE) for Vietnamese manufacturing industries.

Eff 2003 Eff 2004 Eff 2005 Eff 2006 Eff 2007 Average

Total sample 0.293 0. 3 0 1 0.309 0.318 0.326 0.309

Food products & beverages 0.319 0.327 0.334 0.342 0.35 0.334

Textile & wearing apparel 0.242 0.254 0.267 0.279 0.292 0.267

Footwear 0.27 0.3 0.332 0.365 0.398 0.333

Paper & products 0.311 0.326 0.342 0.358 0.374 0.342

Industrial chemicals 0.417 0.417 0.417 0.417 0.417 0.417

Rubber & plastic products 0.349 0.37 0.391 0.412 0.433 0.391

Non-metallic mineral 0.293 0.292 0.29 0.289 0.288 0.290

Basic & fabricated metal 0.321 0.33 0.339 0.347 0.356 0.339

Others 0.291 0.296 0.301 0.306 0.31 0.301

ource: Authors’ estimates from the data source.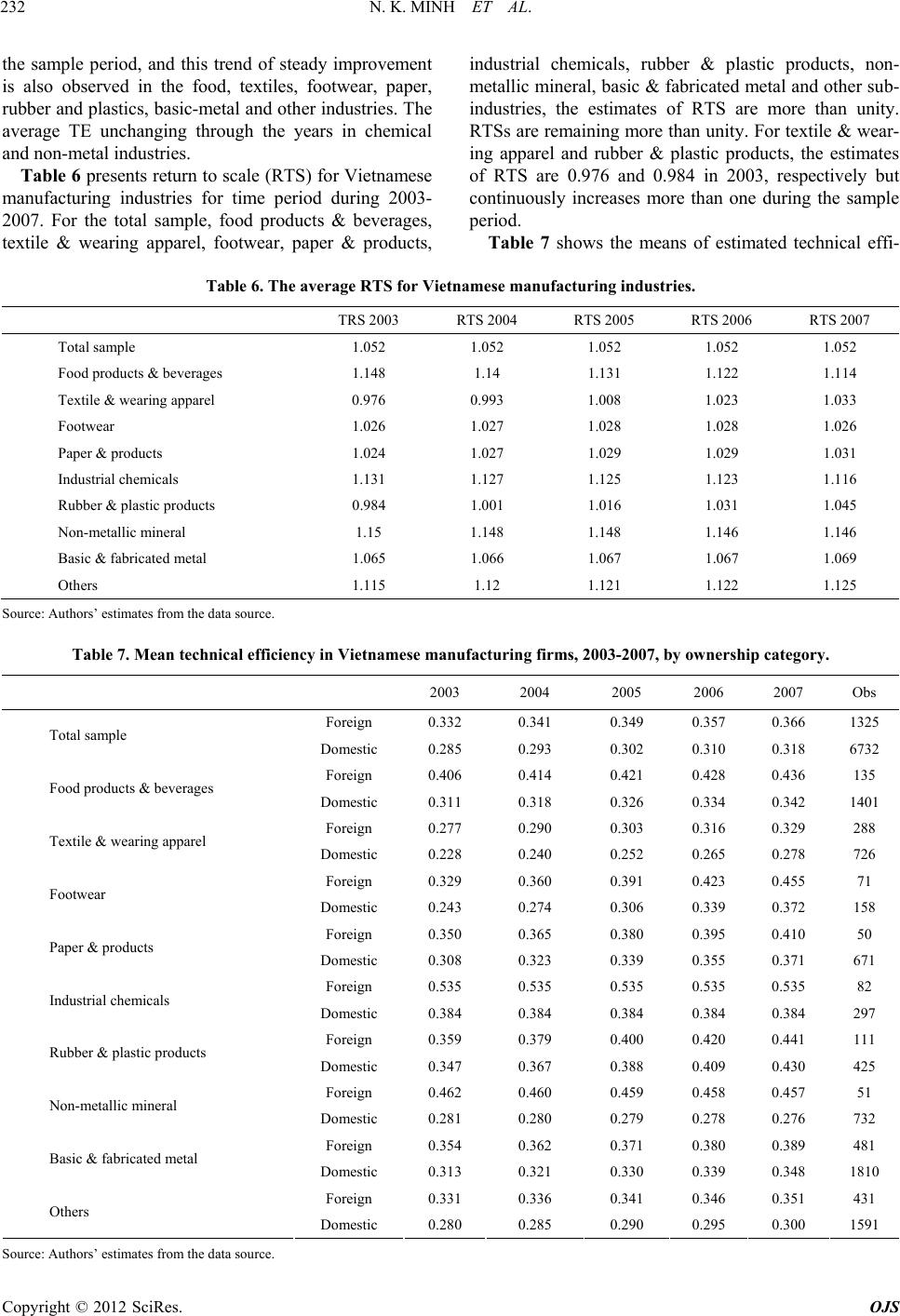

N. K. MINH ET AL.

232

the sample period, and this trend of steady improvement

is also observed in the food, textiles, footwear, paper,

rubber and plastics, basic-metal and other industries. The

average TE unchanging through the years in chemical

and non-metal industries.

Table 6 presents return to scale (RTS) for Vietnamese

manufacturing industries for time period during 2003-

2007. For the total sample, food products & beverages,

textile & wearing apparel, footwear, paper & products,

industrial chemicals, rubber & plastic products, non-

metallic mineral, basic & fabricated metal and other sub-

industries, the estimates of RTS are more than unity.

RTSs are remaining more than unity. For textile & wear-

ing apparel and rubber & plastic products, the estimates

of RTS are 0.976 and 0.984 in 2003, respectively but

continuously increases more than one during the sample

period.

Table 7 shows the means of estimated technical effi-

Table 6. The average RTS for Vietnamese manufac turing industries.

TRS 2003 RTS 2004 RTS 2005 RTS 2006 RTS 2007

Total sample 1.052 1.052 1.052 1.052 1.052

Food products & b e v erages 1.148 1.14 1.131 1.122 1.114

Textile & wearing apparel 0.976 0.993 1.008 1.023 1.033

Footwear 1.026 1.027 1.028 1.028 1.026

Paper & products 1.024 1.027 1.029 1.029 1.031

Industrial chemicals 1.131 1.127 1.125 1.123 1.116

Rubber & plastic products 0.984 1.001 1.016 1.031 1.045

Non-metallic mineral 1.15 1.148 1.148 1.146 1.146

Basic & fabricate d metal 1.065 1.066 1.067 1.067 1.069

Others 1.115 1.12 1.121 1.122 1.125

Source: Authors’ estimates from the data source.

Table 7. Mean technical efficiency in Vietnamese manufacturing firms, 2003-2007, by ownership category.

2003 2004 2005 2006 2007 Obs

Foreign 0.332 0.341 0.349 0.357 0.366 1325

Total sample Domestic 0.285 0.293 0.302 0.310 0.318 6732

Foreign 0.406 0.414 0.421 0.428 0.436 135

Food products & beverages Domestic 0.311 0.318 0.326 0.334 0.342 1401

Foreign 0.277 0.290 0.303 0.316 0.329 288

Textile & wearing apparel Domestic 0.228 0.240 0.252 0.265 0.278 726

Foreign 0.329 0.360 0.391 0.423 0.455 71

Footwear Domestic 0.243 0.274 0.306 0.339 0.372 158

Foreign 0.350 0.365 0.380 0.395 0.410 50

Paper & products Domestic 0.308 0.323 0.339 0.355 0.371 671

Foreign 0.535 0.535 0.535 0.535 0.535 82

Industrial chemicals Domestic 0.384 0.384 0.384 0.384 0.384 297

Foreign 0.359 0.379 0.400 0.420 0.441 111

Rubber & plastic products Domestic 0.347 0.367 0.388 0.409 0.430 425

Foreign 0.462 0.460 0.459 0.458 0.457 51

Non-metallic mineral Domestic 0.281 0.280 0.279 0.278 0.276 732

Foreign 0.354 0.362 0.371 0.380 0.389 481

Basic & fabricated metal Domestic 0.313 0.321 0.330 0.339 0.348 1810

Foreign 0.331 0.336 0.341 0.346 0.351

431

Others Domestic 0.280 0.285 0.290 0.295 0.300 1591

ource: Authors’ estimates from the data source.

N. K. MINH ET AL. 233

ciency for the foreign owned firms, domestically owned

(including private sector firms and public sector firms for

different years during the period, 2003 to 2007).

It is evident from the comparison presented in Table 5

that the mean technical efficiency of foreign firms was

higher than that of domestically owned firms each year

of the period under study. For the five-year period, 2003

to 2007, on an average, technical efficiency of foreign

firms in total sample and sub-samples were higher tech-

nical efficiency than domestically owned firms. The av-

erage technical efficiency levels of foreign firms for in-

dustrial chemicals, non-metallic mineral, footwear over

period 2003-2007 are 0.535, 0.457, 0.455 about, 39, 66

and 22.3 percent higher than that for domestic firms, re-

spectively.

The estimates of the average annual rate of change in

efficiency for the manufacturing industries and some

sub-manufactu ring ind ustries are prese nted in Table 8.

We calculated these efficiency changes using Equation

(2) (Titst ). The rate of growth

in efficiency is an indicator of an industries’ perform-

ance.

echnical change

The estimate of the average rate of growth in effi-

ciency in Vietnamese manufacturing industries suggests

that the level efficiency has increased over the whole

period (except Non-metallic mineral industry). For ex-

ample the sub-industry, with average rate of growth in

efficiency about 8.2% (highest rate) is footwear, follow-

ing by rubber & plastic products (about 6.3%) and textile

& wearing apparel (about 5.4%).

The annual technical progress change estimates for the

manufacturing industry and submanufacturing industries

are presented in Table 9. The technical progress change

index between any two adjacent periods s and t were

calculated directly from the estimated parameters of the

translog stochastic frontier production function by taking

a partial derivative of output with respect to time t. Then,

we calculated technical change for each sub-industry,

and given period by using Equation (3).

Table 10 shows that average technical changes in

manufacturing industry and sub-manufacturing industries

are positive, with an average technical change about 5.2%,

TE TE

Table 8. Technical efficiency change in Vietnamese manufacturing firms, 2003-2007.

TEC 2003-2004 2004-2005 2005-2006 2006-2007 2003-2007

Total sample 0.039 0.04 0.037 0.036 0.030

Food products & b e v erages 0.034 0.03 0.032 0.031 0.025

Textile & wearing apparel 0.071 0.07 0.065 0.062 0.054

Footwear 0.111 0.11 0.099 0.09 0.082

Paper & products 0.065 0.06 0.059 0.056 0.048

Industrial chemicals 0 0 0 0 0.000

Rubber & plastic products 0.087 0.08 0.076 0.07 0.063

Non-metallic mineral –0.006 –0.01 –0.006 –0.006 –0.006

Basic & fabricate d metal 0.036 0.04 0.034 0.033 0.029

Others 0.022 0.02 0.022 0.021 0.017

Source: Authors’ estimates from the data source.

Table 9. Technical progress change in Vietnamese manufacturing firms, 2003-2007.

TPC 2003-2004 2004-2005 2005-2006 2006-2007 2003-2007

Total sample 0.079 0.05 0.011 –0.023 0.023

Food products & b e v erages 0.071 0.05 0.032 0.012 0.033

Textile & wearing apparel 0.041 0.02 –0.011 –0.038 0.002

Footwear 0.047 0.05 0.047 0.047 0.038

Paper & products 0.04 0.01 –0.016 –0.044 –0.002

Industrial chemicals 0.087 0. 0 6 0.041 0.019 0.041

Rubber & plastic products 0.097 0.04 –0.015 –0.071 0.010

Non-metallic mineral 0.102 0.08 0.054 0.03 0.053

Basic & fabricate d metal 0.091 0.05 0.004 –0.039 0.021

Others 0.106 0.06 0.016 –0.029 0.031

Source: Authors’ estimates from the data source.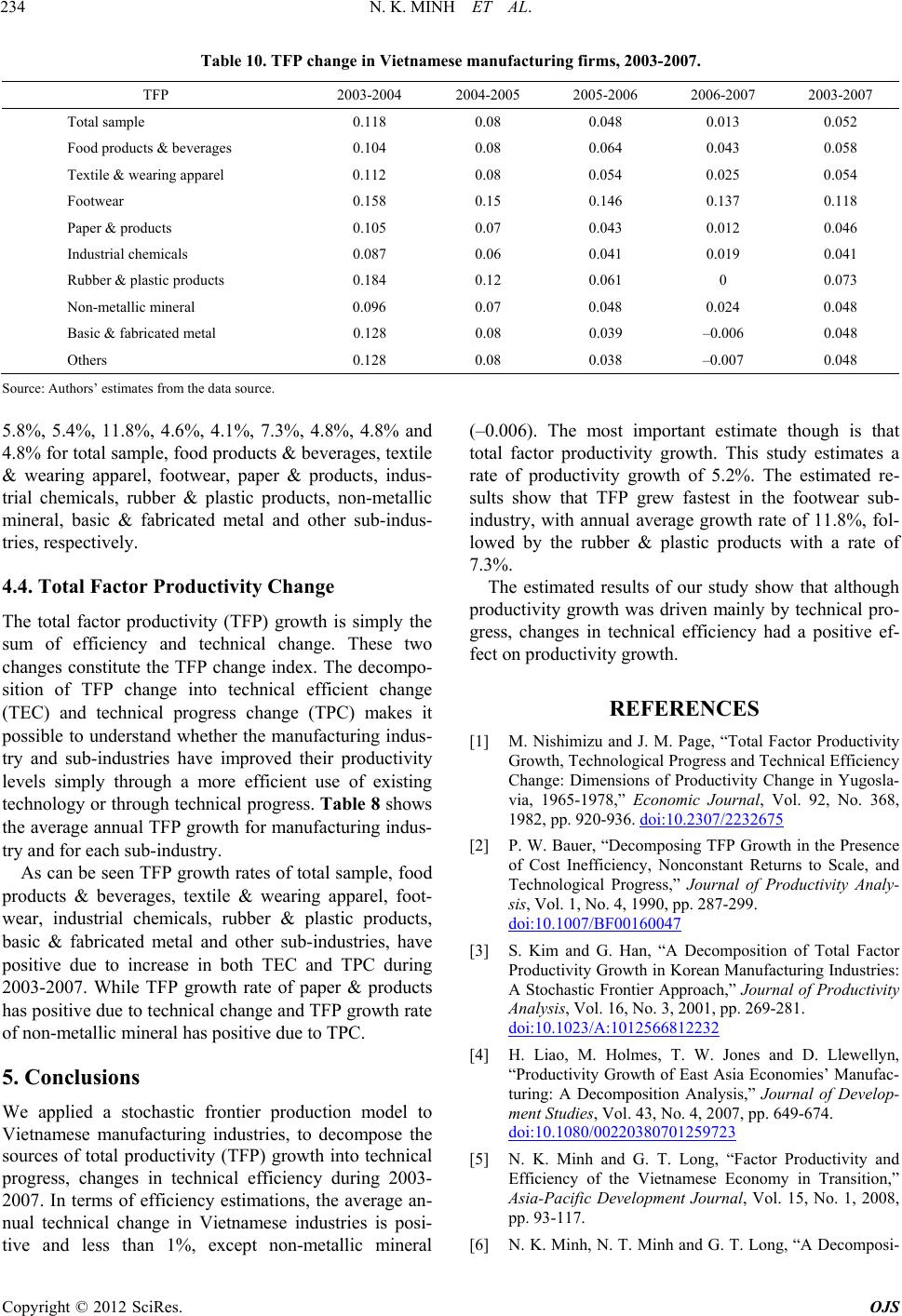

N. K. MINH ET AL.

234

Table 10. TFP change in Vietnamese manufacturing firms, 2003-2007.

TFP 2003-2004 2004-2005 2005-2006 2006-2007 2003-2007

Total sample 0.118 0.08 0.048 0.013 0.052

Food products & b e v erages 0.104 0.08 0.064 0.043 0.058

Textile & wearing apparel 0.112 0.08 0.054 0.025 0.054

Footwear 0.158 0.15 0.146 0.137 0.118

Paper & products 0.105 0.07 0.043 0.012 0.046

Industrial chemicals 0.087 0. 0 6 0.041 0.019 0.041

Rubber & plastic products 0.184 0.12 0.061 0 0.073

Non-metallic mineral 0.096 0.07 0.048 0.024 0.048

Basic & fabricate d metal 0.128 0.08 0.039 –0.006 0.048

Others 0.128 0.08 0.038 –0.007 0.048

Source: Authors’ estimates from the data source.

5.8%, 5.4%, 11.8%, 4.6%, 4.1%, 7.3%, 4.8%, 4.8% and

4.8% for total sample, food products & beverages, textile

& wearing apparel, footwear, paper & products, indus-

trial chemicals, rubber & plastic products, non-metallic

mineral, basic & fabricated metal and other sub-indus-

tries, respectively.

4.4. Total Factor Productivity Change

The total factor productivity (TFP) growth is simply the

sum of efficiency and technical change. These two

changes constitute the TFP change index. The decompo-

sition of TFP change into technical efficient change

(TEC) and technical progress change (TPC) makes it

possible to understand whether the manufacturing indus-

try and sub-industries have improved their productivity

levels simply through a more efficient use of existing

technology or through technical progress. Table 8 shows

the average annual TFP growth for manufacturing indus-

try and for each sub-industry.

As can be seen TFP growth rates of total sample, food

products & beverages, textile & wearing apparel, foot-

wear, industrial chemicals, rubber & plastic products,

basic & fabricated metal and other sub-industries, have

positive due to increase in both TEC and TPC during

2003-2007. While TFP growth rate of paper & products

has positive due to technical change and TFP growth rate

of non-metallic mineral has positive due to TPC.

5. Conclusions

We applied a stochastic frontier production model to

Vietnamese manufacturing industries, to decompose the

sources of total productivity (TFP) growth into technical

progress, changes in technical efficiency during 2003-

2007. In terms of efficiency estimations, the average an-

nual technical change in Vietnamese industries is posi-

tive and less than 1%, except non-metallic mineral

(–0.006). The most important estimate though is that

total factor productivity growth. This study estimates a

rate of productivity growth of 5.2%. The estimated re-

sults show that TFP grew fastest in the footwear sub-

industry, with annual average growth rate of 11.8%, fol-

lowed by the rubber & plastic products with a rate of

7.3%.

The estimated results of our study show that although

productivity growth was driven mainly by technical pro-

gress, changes in technical efficiency had a positive ef-

fect on productivity growth.

REFERENCES

[1] M. Nishimizu and J. M. Page, “Total Factor Productivity

Growth, Technological Progress and Technical Efficiency

Change: Dimensions of Productivity Change in Yugosla-

via, 1965-1978,” Economic Journal, Vol. 92, No. 368,

1982, pp. 920-936. doi:10.2307/2232675

[2] P. W. Bauer, “Decomposing TFP Growth in the Presence

of Cost Inefficiency, Nonconstant Returns to Scale, and

Technological Progress,” Journal of Productivity Analy-

sis, Vol. 1, No. 4, 1990, pp. 287-299.

doi:10.1007/BF00160047

[3] S. Kim and G. Han, “A Decomposition of Total Factor

Productivity Growth in Korean Manufacturing Industries:

A Stochastic Frontier Approach,” Journal of Productivity

Analysis, Vol. 16, No. 3, 2001, pp. 269-281.

doi:10.1023/A:1012566812232

[4] H. Liao, M. Holmes, T. W. Jones and D. Llewellyn,

“Productivity Growth of East Asia Economies’ Manufac-

turing: A Decomposition Analysis,” Journal of Develop-

ment Studies, Vol. 43, No. 4, 2007, pp. 649-674.

doi:10.1080/00220380701259723

[5] N. K. Minh and G. T. Long, “Factor Productivity and

Efficiency of the Vietnamese Economy in Transition,”

Asia-Pacific Development Journal, Vol. 15, No. 1, 2008,

pp. 93-117.

[6] N. K. Minh, N. T. Minh and G. T. Long, “A Decomposi-

N. K. MINH ET AL. 235

tion of Total Factor Productivity Growth in Vietnamese

Manufacturing Industries: A Stochastic Frontier Ap-

proach,” Proceedings of the DEA Symposium, Taiwan,

19-21 January 2010, pp. 164-168.

[7] G. E. Battese and T. J. Coelli, “Frontier Production Func-

tions, Technical Efficiency and Panel Data: With Appli-

cation to Paddy Farmers in India,” Journal of Productiv-

ity Analysis, Vol. 3, No. 1-2, 1992, pp. 153-169.

doi:10.1007/BF00158774