Journal of Transportation Technologies, 2012, 2, 129-143
http://dx.doi.org/10.4236/jtts.2012.22014 Published Online April 2012 (http://www.SciRP.org/journal/jtts)
Modeling of Energy Processes in Wheel-Rail Contacts
Operating under Influence of Periodic
Discontinuous Forces
Zdzislaw Trzaska
Department of Management, Warsaw University of Ecology and Managemenet, Warsaw, Poland
Received December 16, 2011; revised January 22, 2012; accepted February 24, 2012
ABSTRACT
In this paper we present new numerical simulation approaches for determining the energy processes under periodic
conditions caused by time-discontinuous forces in the wheel-rail contacts. The main advantage of the presented method
is the total elimination of frequency analysis, which in effect introduces important simplifications in the identification of
the effects in the contact. The second important feature is the fact that the method is based on the analysis of appropriate
loops on the energy phase plane leading to an easy estimation of the rail strength through the evaluation of the loop’s
area. That model based simulation in the applied dynamics relies on advanced methods for model setup, robust and ef-
ficient numerical solution techniques and powerful simulation tools for practical applications. Fundamental properties
of contact displacements of the rail surface have been considered on the basis of the newly established method. The
contact zone between railway wheels and the rail surfaces made of bulk materials is perceived as strong enough to re-
sist the normal (vertical) forces introduced by heavy loads and the dynamic response induced by track and wheel ir-
regularities. The analysis is carried out for a wheel running on an elastic rail rested on sleepers arranged on completely
rigid foundation. The equations of displacement motion are established through the application of the Lagrange equa-
tions approach. The established model of the wheel-rail contact dynamics has been applied to that same roll plane but
with taking into account a nonlinear characteristic of the sleeper with respect to the ground. Attention then is focused
completely on the modeling of the energy absorbed by the rail. The applied method employs the energy state variables
as time functions leading to determine the susceptibility of a given contact on the strength induced by the rail roll.
Keywords: Wheel-Rail Contact; Energy Process; Periodic Discontinuous Force; One-Period Energy; Energy Loop
1. Introduction
In the analysis of wheel-rail contact several modeling
methods can be applied and in the course of the last dec-
ade new demands have emerged. They are mainly con-
nected with the reduction of costs of maintenance, tech-
nical diagnostics of the track and of railway vehicles, and
elimination of negative effects on the environment. Many
of the works have been related to the increase in train
speed of railway vehicles without affecting safety and
comfort [1-6].
Recently, the advanced technology is confronted in-
creasingly with damping problems that do not address to
issues of scaling. The contact zone (roughly 1 cm2) be-
tween a railway wheel and rail is small compared with
their overall dimensions and its shape depends not only
on the rail and wheel geometry but also on how the
wheel meets the rail influence. Thus, studying the com-
plex motions of railway vehicles could give significant
new insight into the defect properties of materials—a
research domain where relatively little first-principles
progress has been made.
A hard problem arises when the wheel-rail contact is
subject to an action of time-discontinuous forces. It is
well known that in the contact zone between railway
wheel and rail the surfaces and bulk material must be
strong enough to resist the normal (vertical) forces in-
troduced by heavy loads and the dynamic response in-
duced by track and wheel irregularities. Thus, the inter-
actions of the surface and the volume of a solid rail are
important. It is not possible to materials grow without
dislocations and/or other disturbances to crystalline order,
such as vacancies, interstitials, or substitution impurities.
In the case of polycrystalline materials, the memory fea-
tures of hysteresis may be important according to the
methods of their fabrication. Long before defects escalate
to the point of incipient failure, they still influence vibra-
tions. In its simplest form the equations of dynamic mo-
tion of a wheel-rail system are given by a non-linear
C
opyright © 2012 SciRes. JTTs

Z. TRZASKA 130
second order system of ordinary differential equations
(ODEs) of moderate dimension that may be solved nu-
merically by standard methods [7-17].
The goal of this paper is to assist the subject progress
towards a healthier balance between these extreme fac-
tors. The main attention is focused on modeling of the
energy absorbed by the rail rested on an elastic sleeper
and completely rigid foundation. To determine the su-
sceptibility of a given contact to the strength induced by
the rail roll, an approach employing the energy state
variables (time functions) is established. Then, the estab-
lished model of the wheel-rail contact dynamics has been
applied to that same roll plane but with taking into ac-
count a nonlinear characteristic of the sleeper with re-
spect to the ground. We conclude that under operations
of periodic discontinuous forces the energy absorbed in
contact can be measured by loops of one-period energy
in the energy phase plane. Several numerical examples
are included.
2. The Problem Description
The contact between wheel and rail is the basic constitu-
tive element of railway vehicle dynamics. For its model-
ing two aspects have to be considered: 1) the geometric
or kinematical relations of the wheel-rail contact, and 2)
the contact mechanical relations for the calculation of the
contact forces. Strictly connected to contact mechanics is
the problem of formation of corrugations on the rail treat,
which is now in the centre of attention of many research
teams. The knowledge of railway vehicle dynamics al-
lows us to predict with confidence what the values of
contact stress, tangential creep forces and creep age in
the wheel/rail contact patch are for a wide range of dif-
ferent conditions. This gives a valuable insight into the
influence of the many different factors that affect the
incidence of rolling contact fatigue in rails due to the
combination of these parameters [18-27].
At present, many scientific centers in the world are
involved in research focused on different problems of
railway vehicle dynamics. Increasing operational speeds
and comfort demands require focusing on both riding
qualities of railway vehicles, transport safety and comfort.
Several factors have a negative influence on ride comfort,
and emphasize the necessity of more advanced suspen-
sions. As the challenges of higher speed and higher loads
with very high levels of safety require ever more innova-
tive engineering solutions, better understanding of the
technical issues and use of new computer based tools is
required [27-35].
Usually, railway vehicles operating in modern coun-
tries use wheel sets comprising two wheels fixed to a
common axle (Figure 1). Wheels are rigidly connected
with the axle and roll in the direction which they are
heading for. As both wheels are rotating at the same
(a)
b)
1360 mm
20 KN
4 mm
1435 mm
Plane resting
across the tops o
f
the two inclined
rails
(b)
Figure 1. Schematic views: (a) Train vehicle; (b) Wheels,
axle, rail and sleeper.
speed, the contact forces ultimately are repartitioned
symmetrically on both wheels. These forces are a major
cause of the rails wear.
A completely linear multi-body formalism must be
taken into considerations and the kinematical nonlinear-
ity can be replaced by quasi-linearization. Strictly con-
nected to contact mechanics is the problem of formation
of corrugations on the rail treat, which is now in the cen-
tre of attention of many research teams [2,21].
The development of rolling contact fatigue in rails de-
pends on the interplay between crack growth, which is
governed by the contact stress and the tangential force at
the contact patch. Moreover, the wear depends on the
tangential force and the creep age at the contact patch
(Figure 2). These parameters are dependent on a large
number of inter-dependent factors, in particular:
 Vehicle Configuration: wheelbase, axle load, wheel
diameter,
 Suspension design: in particular primary yaw stiff-
ness,
 Track geometric quality,
 Wheel profiles: nominal profile and state of wear,
 Rail profiles: nominal profile and state of wear,
 Wheel/rail friction,
 Cant deficiency (depending on speed, radius and
cant),
 Traction and braking forces,
 Wheel and rail material properties.

Z. TRZASKA 131
(a) (b)
Figure 2. Spalling from high contact stresses of the: (a) Rail;
(b) Wheel.
The estimates have showed that in the case of the
wheel-rail system, the elastic correlation length far ex-
ceeds the length of the contact region (about 1 cm). Mul-
tibody dynamics and wheel-rail contact models make
detailed analysis possible not only for ride and handling,
but also for determining their effects on rail non-uni-
formities. Experimental studies have revealed that esti-
mations of both the size of the contact region and pres-
sure distribution in the contact depend on the accuracy of
which the surface micro-relief was determined.
The size and shape of the contact zone where the rail-
way wheel meets the rail can be calculated with different
techniques. The surfaces of railway wheels and rails, as
many other technical surfaces, have micro-heterogenei-
ties at many scale levels; by experimental studies it has
been established that these are self-similar surfaces in the
wide range of surface scales and can be referred to the
class of fractal ones [9,10]. This suggests that both the
size of the contact region and pressure distribution in the
contact depend on the accuracy with which the surface
micro-relief can be determined.
Through mathematical analysis it is possible to build a
deep and functional understanding of the wheel-rail in-
terface, suspension and suspension component behavior,
simulation and testing of mechanical systems interaction
with surrounding infrastructure, noise and vibration.
3. Dynamic Model of Wheel-Rail Contacts
The contact between wheel and rail is the constitutive
element of railway vehicle dynamics. The geometric or
kinematical relations of the wheel-rail contact and the
contact mechanical relations for the calculation of the
contact forces are to be dealt with very careful attention.
This can be done within a completely linear multi-body
formalism taking into account kinematical nonlinearities
by quasi-linearization. From the short-term dynamic cal-
culations a periodic non-harmonic motion can be ob-
tained in terms of the generalized displacements. For the
subsequent calculation of stress only typical contact
characteristics are of interest. As is well known the po-
tential and success of vehicle-track dynamic simula-
tions very much depends on how well the system is
mathematically modeled and fed with pertinent input
data. We use a simplified dynamic model for the wheel
set and rail contact. The wheelset is running on straight
track and the wheelset and track are considered as rigid
bodies. Any contact stiffness is included. However, the
contact stiffness is not the only one elasticity to be taken
into account, and the track stiffness itself can be used to
smooth out the load variation.
A large part of the wheel-rail contact modelisation
leads to the load transfer when flanging, and more gener-
ally when there is a jump between two contact points on
the profiles. We assume that the wheelset is rigid and in
the rail model the discrete sleepers under the rail are
resting on completely rigid foundation. The interface
between the wheel and the rail is a small horizontal con-
tact patch. The contact pressure on this small surface is
closer to a stress concentration than in the rest of the
bodies. The centre of this surface is also the application
point of tangential forces (traction and braking Fx, guid-
ing or parasite forces Fy, see Figure 3). The knowledge
of these forces is necessary to determine the general
wheelset equilibrium and its dynamic behavior.
For the overall model we need to consider all specific
phenomena occurring in the system during the train
movement on the rail. To have a large set of information
on the contact, as a function of the vertical relative dis-
placement dz the study of a single wheel-rail pair is
enough. The first modelisation of the flange contact has
been presented to consider it as an elastic spring whose
value comes from the track and the rail beam deforma-
tion. For these purposes we consider a scheme presented
in Figure 4. The rail is considered as Timoshenko beam
which can be divided into small segments so that a
sleeper is assigned to every segment. The sleeper has
both a mass and the pad between rail and sleeper and the
ballast are replaced by springs and dampers. As a natural
improvement a more complex model is also considered.
It takes into account the roll effect of the other wheel-rail
pair of the wheelset. The lateral displacement and the yaw
x
z
y
0
Figure 3. Rail, wheel and contact frames.

Z. TRZASKA 132
F
sleepe
r
rigid foundation
F
F F
Figure 4. Subdivision of the wheel-tr a c k se t into se gments.
angle can be considered as two small displacements rela-
tive to the track and they do not exceed approximately
±1%. Then we take into account the fact that the
wheelsets are connected to the chassis of the bogies by a
set of joints, which control the relative motion between
wheels and chassis, and by a set of springs and dampers.
In turn, the bogie chassis is connected to a support beam
to which one of the carshell connecting shaft is attached.
The connection between chassis and support beam is also
done by a set of kinematic joints, springs and dampers,
designated by secondary suspension [13,28]. Each train
carbody is generally mounted in the top of two bogies.
The attachment between the carbody and each bogie is
done by a shaft rigidly connected to the carbody that is
inserted in a bushing joint located in the support beam of
the bogie. Moreover, the rail remains in its original 1in20
or 1in40 inclined position. Measured values showed a
maximum of about 0.3 and 0.95 degrees respectively for
the UK and German sites. In light of this reason it is as-
sumed for the developments that follow that the motion
of each wheelset tracks exactly the geometry of the rail-
way and lateral inclinations can simply be ignored during
numerical simulation.
The rail structure is particularly subjected to dynamic
load, which is induced by moving wheels of the vehicles.
This dynamics action can excite vibrations of the track,
contribute to bad track conditions and consequently
lower the comfort of traveling. The dynamic analysis of
the rail structure subjected to a moving load is a very
complex problem. Such models can be used for the
simulation of real actions of vehicles and detailed re-
sponse of the structure can be obtained. When an elastic
body, such as a wheel, is pressed against another elastic
body, such as a rail, so that a normal load is transmitted
and a contact area is formed. As the elastic deformation
in the vicinity of the contact area is small its effect on the
stress response cannot be neglected. Then, assuming that
in the vicinity of the contact patch the curvatures of the
wheel and rail are constant, the imprinted contact patch is
small compared with the radii of curvature and the di-
mensions of the wheel and rails, the contacting bodies
can be represented by elastic half-spaces and their shape
can be approximated by quadratic surfaces. Usually it
can be assumed that the material properties of wheel and
rail are the same and in this case it can be shown that the
tangential tractions do not affect the normal pressures
acting between the bodies. Then with these assumptions,
for the case where the wheels and rails are smooth, the
dimensions of the contact area can be obtained from the
theory of Kalker described in [28].
Thus, we can consider the stationary rolling contact of
elastic bodies and suppose that material properties of
wheel and rail are the same, i.e. the bodies in contact are
quasi-identical. In this case the contact problem trans-
lates to the normal action between the wheel and rail. It
means that the normal pressure at a point of the contact
patch is proportionate to the interpenetration of the con-
tact bodies at the point.
In this system, inertial, stiffness and damping proper-
ties vary piecewise-continuously with respect to the spa-
tial location. A continuously vibrating system may be
approximately modeled by an appropriate set of lumped
masses properly interconnected using discrete spring and
damper elements (Figure 5). An immediate advantage
resulting from this lumped-parameter representation is
that the system governing equations become ordinary
differential equations. A linear model is usually justified
on the basis of small corresponding deflections.
For each of such segments as that shown in Figure 5 a
system of equations can be formulated as follows

0
0
0
M
zb bz
rrr
M
zbbb z
s
srrs
kkz Ft
rr
kkk z
rrs s





s

  

  

  






 
 (1)
F
Mr
Ms
br
bs
kr
ks
z
zs
Figure 5. Elementary section of the loaded rail.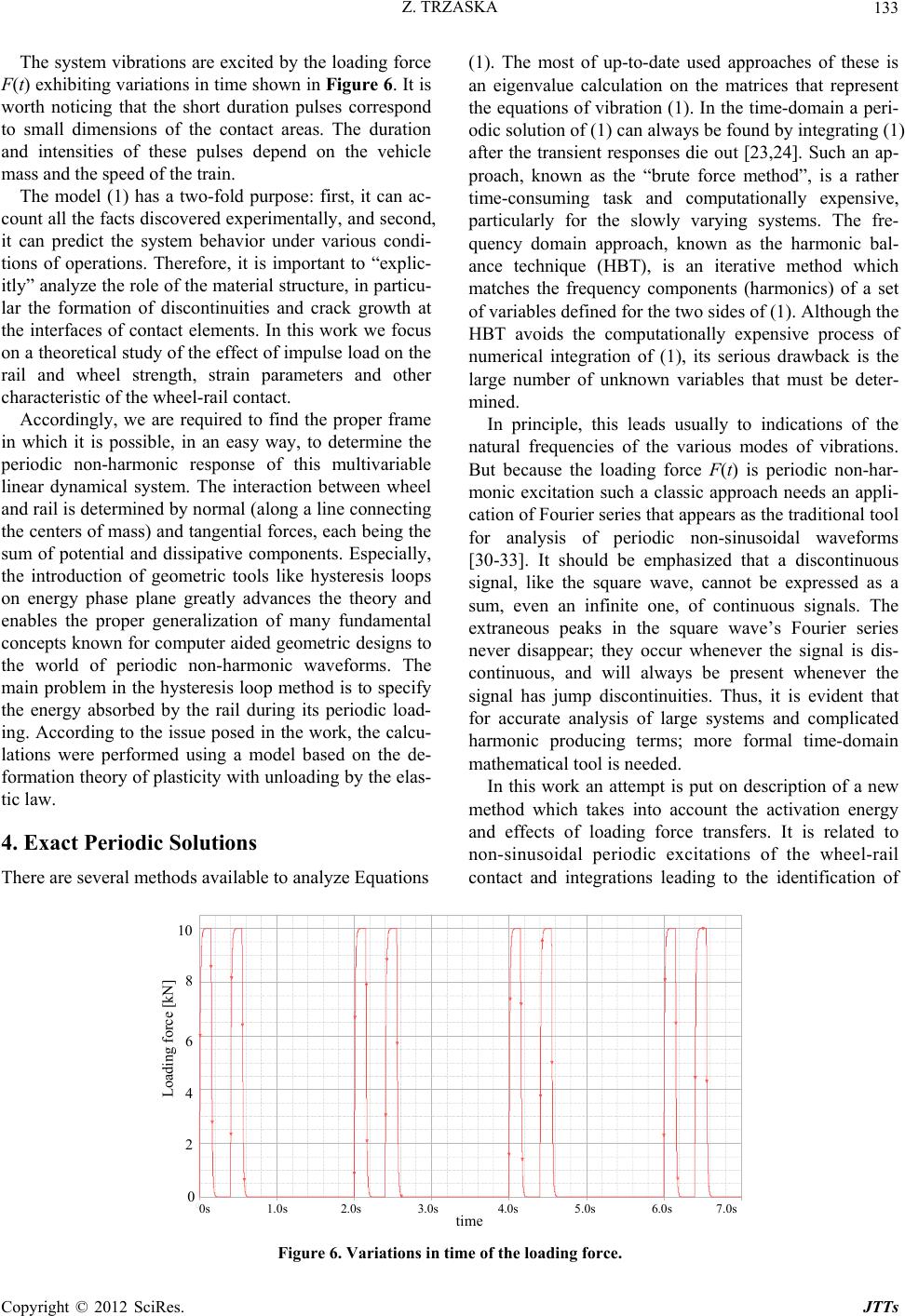

Z. TRZASKA 133
The system vibrations are excited by the loading force
F(t) exhibiting variations in time shown in Figure 6. It is
worth noticing that the short duration pulses correspond
to small dimensions of the contact areas. The duration
and intensities of these pulses depend on the vehicle
mass and the speed of the train.
(1). The most of up-to-date used approaches of these is
an eigenvalue calculation on the matrices that represent
the equations of vibration (1). In the time-domain a peri-
odic solution of (1) can always be found by integrating (1)
after the transient responses die out [23,24]. Such an ap-
proach, known as the “brute force method”, is a rather
time-consuming task and computationally expensive,
particularly for the slowly varying systems. The fre-
quency domain approach, known as the harmonic bal-
ance technique (HBT), is an iterative method which
matches the frequency components (harmonics) of a set
of variables defined for the two sides of (1). Although the
HBT avoids the computationally expensive process of
numerical integration of (1), its serious drawback is the
large number of unknown variables that must be deter-
mined.
The model (1) has a two-fold purpose: first, it can ac-
count all the facts discovered experimentally, and second,
it can predict the system behavior under various condi-
tions of operations. Therefore, it is important to “explic-
itly” analyze the role of the material structure, in particu-
lar the formation of discontinuities and crack growth at
the interfaces of contact elements. In this work we focus
on a theoretical study of the effect of impulse load on the
rail and wheel strength, strain parameters and other
characteristic of the wheel-rail contact.
Accordingly, we are required to find the proper frame
in which it is possible, in an easy way, to determine the
periodic non-harmonic response of this multivariable
linear dynamical system. The interaction between wheel
and rail is determined by normal (along a line connecting
the centers of mass) and tangential forces, each being the
sum of potential and dissipative components. Especially,
the introduction of geometric tools like hysteresis loops
on energy phase plane greatly advances the theory and
enables the proper generalization of many fundamental
concepts known for computer aided geometric designs to
the world of periodic non-harmonic waveforms. The
main problem in the hysteresis loop method is to specify
the energy absorbed by the rail during its periodic load-
ing. According to the issue posed in the work, the calcu-
lations were performed using a model based on the de-
formation theory of plasticity with unloading by the elas-
tic law.
In principle, this leads usually to indications of the
natural frequencies of the various modes of vibrations.
But because the loading force F(t) is periodic non-har-
monic excitation such a classic approach needs an appli-
cation of Fourier series that appears as the traditional tool
for analysis of periodic non-sinusoidal waveforms
[30-33]. It should be emphasized that a discontinuous
signal, like the square wave, cannot be expressed as a
sum, even an infinite one, of continuous signals. The
extraneous peaks in the square wave’s Fourier series
never disappear; they occur whenever the signal is dis-
continuous, and will always be present whenever the
signal has jump discontinuities. Thus, it is evident that
for accurate analysis of large systems and complicated
harmonic producing terms; more formal time-domain
mathematical tool is needed.
In this work an attempt is put on description of a new
method which takes into account the activation energy
and effects of loading force transfers. It is related to
non-sinusoidal periodic excitations of the wheel-rail
contact and integrations leading to the identification of
4. Exact Periodic Solutions
There are several methods available to analyze Equations
0s1.0s 2.0s
3
.0s
4
.0s
5
.0s
6
.0s 7.0s
Loadin
g
force
[
kN
]
10
8
6
4
2
0
0s 1.0s 2.0s 3.0s 4.0s 5.0s 6.0s 7.0s
Time
time
Loading force [kN]
Figure 6. Variations in time of the loading force.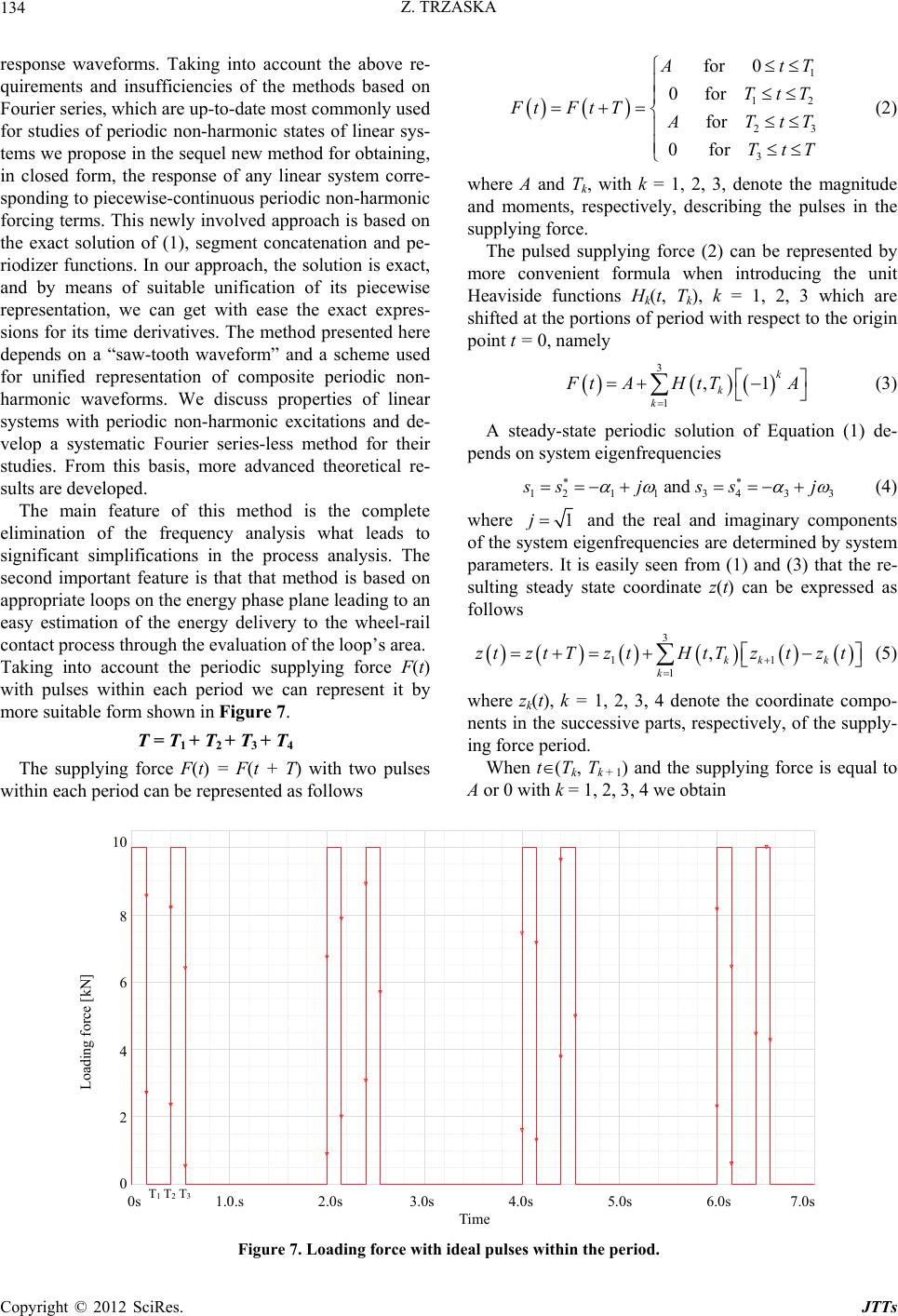

Z. TRZASKA 134
response waveforms. Taking into account the above re-
quirements and insufficiencies of the methods based on
Fourier series, which are up-to-date most commonly used
for studies of periodic non-harmonic states of linear sys-
tems we propose in the sequel new method for obtaining,
in closed form, the response of any linear system corre-
sponding to piecewise-continuous periodic non-harmonic
forcing terms. This newly involved approach is based on
the exact solution of (1), segment concatenation and pe-
riodizer functions. In our approach, the solution is exact,
and by means of suitable unification of its piecewise
representation, we can get with ease the exact expres-
sions for its time derivatives. The method presented here
depends on a “saw-tooth waveform” and a scheme used
for unified representation of composite periodic non-
harmonic waveforms. We discuss properties of linear
systems with periodic non-harmonic excitations and de-
velop a systematic Fourier series-less method for their
studies. From this basis, more advanced theoretical re-
sults are developed.
The main feature of this method is the complete
elimination of the frequency analysis what leads to
significant simplifications in the process analysis. The
second important feature is that that method is based on
appropriate loops on the energy phase plane leading to an
easy estimation of the energy delivery to the wheel-rail
contact process through the evaluation of the loop’s area.
Taking into account the periodic supplying force F(t)
with pulses within each period we can represent it by
more suitable form shown in Figure 7.
T = T1 + T2 + T3 + T4
The supplying force F(t) = F(t + T) with two pulses
within each period can be represented as follows
 
1
1
23
3
for 0
0 for
for
0 for
2
A
tT
TtT
FtFt T
A
TtT
TtT









(2)
where A and Tk, with k = 1, 2, 3, denote the magnitude
and moments, respectively, describing the pulses in the
supplying force.
The pulsed supplying force (2) can be represented by
more convenient formula when introducing the unit
Heaviside functions Hk(t, Tk), k = 1, 2, 3 which are
shifted at the portions of period with respect to the origin
point t = 0, namely
  
3
1
,1
k
k
k
F
tA HtTA


 



3
(3)
A steady-state periodic solution of Equation (1) de-
pends on system eigenfrequencies
121 1343
and
s
sjssj



   (4)
where 1j and the real and imaginary components
of the system eigenfrequencies are determined by system
parameters. It is easily seen from (1) and (3) that the re-
sulting steady state coordinate z(t) can be expressed as
follows
    
3
11
1
,kk k
k
ztztTz tHtTztzt


  

 (5)
where zk(t), k = 1, 2, 3, 4 denote the coordinate compo-
nents in the successive parts, respectively, of the supply-
ing force period.
When t(Tk, Tk + 1) and the supplying force is equal to
A or 0 with k = 1, 2, 3, 4 we obtain
Loading force [kN]
10
8
6
4
2
0
0s 1.0.s 2.0s 3.0s 4.0s 5.0s 6.0s 7.0s
Time
T
1
T
2
T
3
Figure 7. Loading force with ideal pulses within the period.

Z. TRZASKA 135

4
,
1
m
st
kmk
m
ztBe Z


,
fk
(6)
where Zf,k denotes the steady state term forced by Fk and
Bm,k , m = 1, 2, 3, 4, are constants to be determined from
continuity and periodicity conditions fulfilled by respect-
tive components of the system whole response.
The steady state forced term Zf,k follows from Equa-
tions (1) when successively substituting Fk, respectively.
In result we get
,
rs
f
k
rs
kk
k
Z
F
kk

 (7)
To determine integration constants Bm,k we take into
account the continuity and periodicity conditions which
must be fulfilled by the coordinates z(t) and zs(t) [10].
For the sake of compactness of presentation we trans-
form Equation (1) into standard state variable equation
 
1
tt

xAxgt
(8)
where vectors x(t) and g(t) as well as constant element
matrix A1 have appropriate dimensions.
Here it is worth noticing that A1 must be non-critical
with respect to T, i.e. the relation

1
det 0
T
e
A
I (9)
must be fulfilled.
Since all eigenvalues of the studied system have nega-
tive real parts, it is clear that A1 is non-critical and the
condition (9) is satisfied. We now turn to describe an
algorithm to compute a periodic solution for (8). The
procedure for obtaining the steady state solutions of (8) is
as follows.
The periodizer function

π
arctan cot
2π
TT
pt t
T


 




(10)
is established to have period T. In the presented proce-
dure we construct the solution for one period [0, T) and
then extend that solution to be periodic on the whole t
line. This process is called the segment concatenation.
Generalizing (3) to the case of forcing term in (8) we
represent g(t) by a set of continuous terms gk(t) in the
subintervals of [0, T). Such a division yields the respect-
tive solutions xk(t) of x(t) that are determined as

1,
t
kk
f
k
te
A
xJX (11)
for k = 1, 2, 3 ,4, where Xf,k is a forced steady state (index
f) solution of (8) and has the same waveform shape as
that of gk(t) in the corresponding subinterval, and Jk is a
constant vector to be determined. We can find vectors Jk
by analyzing the periodicity condition for the total solu-
tion as follows
1
1,1
T
fe
A
4
J
xJ
,1
X


(12)
and from the continuity conditions it follows that
11
,1
TT
kk
kfkk fk
ee

 X
AA
JJ (13)
for k = 1, 2, .3.
Because the period [0, T) is divided into subintervals
[tk, tk+1), k = 0, 1, 2, 3, then (12), (13) yield the block
matrix equation
1
,1
1
12 12,1
2
12 12,3
3
13 13,3
4
00
00
00
00
T
f
TT
f
TT f
TT f
e
ee
ee
ee






 



















A
AA
AA
AA
IX
J
X
J
X
J
X
J
(14)
From the Kronecker-Weierstrass form [35] it follows
that the system (14) has a unique solution {J1, ··· , J4}
for any T, t1, ··· , t3, and A1 Using the periodizer function
p(t) we sew on continuous solutions in all subintervals
during the concatenation process yielding periodic steady
state solutions. Because the solutions are exact, the typi-
cal drawbacks of classical methods, such as the Gibbs
effect [5], are avoided
5. One-Period Energy Conception
The approach presented in the previous sections can be
applied to compute energy delivered by the independent
supplying force to the load elements. Under periodic
conditions the delivered energy is measured by one pe-
riod energy loops on the energy phase plane. This new
concept has been discussed in more details in the recent
papers [32-34]. Then the total energy, WT delivered by
supplying force F(t) = F(t + T) in one period equals
 

0(0)
dd
zT
T
T
z
WFtvtt Ftzt

(15)
where




vt zt

 denotes the velocity of the rigid rail
oscillations. The above integral is of the Riemann-
Stieltjes type. The solutions obtained by using the perio-
dizer and concatenation procedure can be easily used in
(15) to find WT. We illustrate the concatenation proce-
dure with two numerical examples.
Example 1. Consider a particular case of the system
shown in Figure 5 with forcing term F(t) characterized
by A = 110 kN, T1 = 0.15 s, T2 = T3 = T = 2 s and M =
110 kg. The rigid sleeper is directly incorporated to the
rigid foundation. We take into account the remaining
parameters: br = 632 Ns/m and kr = 2.5 kN/m. Perform-
ing computations in accord to the above presented algo-
rithm yields the one-period energy loop that is presented
in Figure 8. It can be easily found that the energy deliv-
ered by the loading force F(t) equals WT = 110 kN·0.6
cm = 0.66 kJ.

Z. TRZASKA 136
For the comparison purposes we have considered the
same as the above system but with F(t) =110 sin(20 πt)
kN. The result of computation is presented in Figure 9.
Note, that sinusoidal loading force of the same magni-
tude excites vibrations exhibiting much smaller magni-
tude and delivers smaller one-period energy than in the
case of pulsed force. Figure 9 shows the one period en-
ergy loop involved by sinusoidal loading force. The
one-period energy was computed by using the Matlab
function quad.m to yield WTsin = 0.124 kJ.
Example 2. Let us consider the system shown in Fig-
ure 5 with an elastic sleeper that is connected with the
rigid foundation with a spring and a damper. The data
given in Example 1 are supplemented with the sleeper
mass Ms = 156 kg and remaining parameters: bs = 520
Ns/m and ks = 1.5 kN/m. For the above taken data we
have determined the one-period energy loop that is
shown in Figure 10. The computed one-period energy
equals WT2 = 1.485 kJ.
It has to be noted that for the loading force exhibiting
two identical pulses within the period the magnitude of
the rail vibrations is much greater and the one-period
energy delivered to the system is more than five times
greater with respect to the case of one pulse within the
period. If the loading force F(t) takes sinusoidal form
with the same magnitude and frequency f = 10 Hz then
the one period energy delivered to the system has the
form shown in Figure 11. The area of this loop equals
- 10 0 20 40 60 80 100 120
F(t) [kN]
Z
(
t
)
[
cm
]
1.0
0.5
0
-0.5
Figure 8. One-period energy loop for loading force with one pulse within the period and rigid sleeper.
-150 -100 -50 050 100 150
-150
-100
-50
0
50
100
150
F
(
t
)
[kN]
z(t)[mm]
1.5
1.0
0.5
0
-0.5
-1.0
-1.5
-150
Figure 9. One-period energy loop for sinusoidal loading force.

Z. TRZASKA 137
0 25 50 75 100
F(t) [kN]
Z(t)
[cm]
2
1
0
-1
Figure 10. One-period energy loop for loading force with two pulses wi thin the period and elastic sleeper.
–
100 –50 0 50 100
F
sin
(t)[kN]
15
10
5
0
–5
–10
–15
Z
sin
(t)[kN]
Figure 11. One-period energy loop for sinusoidal loading force and elastic sleeper.
WTsin2 = 1.125 kJ. Because the frequency range of interest
is very limited in the involved model of the wheel-rail
contact a linear spring in parallel with a linear viscous
damper (dashpot) is sufficient here. For larger frequency
ranges this model can be easily transformed into appro-
priate one that provides strong frequency dependence,
giving a very significant stiffness and damping at high
frequencies. The presented methodology can be applied
to predict the durability of wheel rail systems subject to
wear and crack growth. Under the action of the cyclic
load obtained from the contact calculation the growth of
the crack can be predicted. All eigendamping properties
of rubber elements, as well as other parasitic damping
must be considered in the model parameters for correct
modeling.
Some unfavorable conditions that are particularly det-
rimental for ride comfort are:
 low damping or even instability of the car body mode
initiated through the coupling of the self-excited si-
nusoidal wheel movement with rail and sleeper ei-

Z. TRZASKA 138
genmodes;
 resonance from the eigenmode of the vehicle compo-
nents with the periodic excited loading force.
To study the influence of vehicle speed, we have to
consider the excitation by track unevenness. This prob-
lem is not considered in this paper for the sake of pres-
entation compactness. In the next Section influences of
nonlinear characteristics of the elastic support will be
considered.
6. Sleeper Nonlinear Characteristics
In order to check the efficiency of the proposed method
which completely eliminates the Fourier series approach
as well as to exhibit its advantages in applications the
above established model of the wheel-rail contact dy-
namics has been applied to that same roll plane but with
taking into account a nonlinear characteristic of the
sleeper with respect the ground. It is represented by the
relation



2
22
3
s
ss
f
zk zz   (16)
where constant parameters k2, α and β can be considered
as bifurcating values. For α = 1.75, β = –1 the plot of the
relative value f2/k2 is shown in Figure 12.
In our approach, periodic solutions were determined
by appropriate modifications of standard numerical solver
used for solutions of nonlinear ordinary differential
equations [36]. They appear as computationally not ex-
pensive alternatives to the traditional harmonic balance
approach and lead to quite satisfactory results. For a set
of system parameters and the forcing term shown in
Figure 7 and nonlinearity presented in Figure 12 the
calculated time variations of the wheel-rail contact de-
formations are depicted in Figure 13. Then using the
alternative expression for the one-period energy,
 


00
dd
PT
T
T
P
WFtvtt vtPt

(17)
where




0d
t
Pt F

  denotes the force impulse we
can determine the energy absorbed by the rail during
one-period of the applied force. The corresponding loop
of one-period energy is presented in Figure 14. Applying
suitable numerical procedure we can evaluate the loop
surface which determines the energy absorbed by the rail
during one-period of the force action. It takes value of
3.0 kJ. Observe that the nonlinearity influences the en-
ergy absorbed by the rail at the contact of the wheel and
rail in an important way. However, one can notice that
the nonlinearity increases the absorbed energy in the
contact. This is mainly due to the fact that, in these for-
mulations, the motion of the wheel is assumed to travel
with a constant forward velocity. Moreover, parameter
-1 -0.500.5 11.5 2
0
0. 5
1
1. 5
zs(t)[cm]
f2(
zs
)/k2
Nonlinear characteristic of the elastic sleeper
z
s
(t)[cm]
Nonlinear characteristic of the elastic sleeper
f
2
(zs)/k
2
Figure 12. Nonlinear characteristic of the sleeper stiffness.

Z. TRZASKA 139
010 20 30 40 50 60 70 80 90 10
0
-9
-8
-7
-6
-5
-4
-3
-2
-1
0x 10
-
3
time[s]
z
time [s]
z
× 10
–3
Figure 13. Deformation of the wheel-rail contact.
00.5 11.5 2
0
5
10
15 x 10
-3
P(t)*10
-2
[Ns]
v(t)
Loop of one-period energy
P(t)·10
-2
[Ns]
v(t)
Loop of one period energy
Figure 14. Loop of one-period energy.

Z. TRZASKA 140
estimation is an important problem, because many pa-
rameters simply cannot be measured physically with
good accuracy, especially in real-time applications. One
of the advantages of the one-period energy approach
used in this study is that when the number of nonlinear
elements is increased, the form of the input force impulse
remains unchanged and results of computer simulations
can be used directly to estimate the energy absorbed by
the rail.
It can be noticed that when using the minimum num-
ber of input force pulses required to perform the estima-
tion of the absorbed energy, i.e. a number of excitation
points equal to the number of wheels in one side of the
bogie, it leads to decreasing the number of particular
areas in the resulting loop of one-period energy and add-
ing extra information into an algorithm for whole loop
surface evaluations.
Although the proposed technique has been applied in
order to identify parameters of a real mechanical system
its use to solve analogous problems in other fields of
human activities is recommended.
The problem may find applications in multi-body dy-
namics as well, including dynamic vibration absorbers,
while other applications include bridges, aircraft struc-
tures, and turbo-machinery blades.
7. Discussion and Conclusions
The introduction of damping elements into the model
might well result in a change in the computed critical
speed. The elementary analysis given in this chapter
gives a good idea of the complexities involved in the
stability analysis for rail vehicles but also shows that
there are some similarities between the stability problems
of railcars and other vehicles.
The dynamics of the situation when the wheelset is not
exactly centered and has a small yaw angle with respect
to the rails will be subsequently studied. The interaction
between steel wheels and steel rails is actually quite
complex but for a linear stability analysis, a simplified
treatment is adequate.
When there are lateral and longitudinal forces between
the wheel and the rail, the contact point on the wheel will
exhibit rather small apparent relative velocities with re-
spect to the rail in the lateral and longitudinal directions.
The existence of a creepage does not imply a sliding ve-
locity between the wheel and the rail.
The introduction of damping elements into the model
might well result in a change in the computed critical
speed.
The dynamics of the situation when the wheelset is not
exactly centered and has a small yaw angle with respect
to the rails will be subsequently studied. It seems that the
existence of a creepage does not imply a sliding velocity
between the wheel and the rail. The formation of non-
elliptical contact patches for real profile combinations
and the so-called transient contact problem, which is
important for high frequency vibration of wheel and rail,
may give an attempt leading to a general view of the
problems of contact mechanics concerning complete as-
pects of wheel-rail contact.
The results may predict how many cycles are required
for the crack to grow to a critical size and the crack
growth rate. The methods and tools presented can be
applied to provide critical design information for engi-
neers responsible for railway system durability.
Theoretical models describing the interaction between
a railway wheel and the track were used for studying the
wheel and track vibrations. The main emphasis has been
put on one-period energy delivered to the rail by the
loading force exerted by the railway vehicle. This is in
response to modern technological demands where the
couplings and interactions between various components
of the model is a central mechanism in controlling the
system. Accordingly, the proper frame in which it is pos-
sible, in an easy way, to determine the periodic non-
harmonic response of multivariable linear dynamical
systems was presented. The load transfer has been calcu-
lated on the basis of the elastic deformation in the
neighborhood of each contact. In practice, the dynamic
response of vehicles also has a significant influence on
the rolling contact fatigue behavior. It has been shown
that the time domain representation of a system by means
of the concatenation procedure, as opposed to the fre-
quency domain representation by means of the system
transfer function, has become more advantageous ap-
proach to the exhibition of system dynamics in periodic
non-harmonic states. Especially, the introduction of
geometric tools like hysteresis loops on energy phase
plane greatly advances the theory and enables the proper
generalization of many fundamental concepts known for
computer aided geometric designs to the world of peri-
odic non-harmonic waveforms. The fatigue damage and
rail corrugation can be treated as a further development
of this research.
For the comparative purposes we have considered the
case presented in Example 1 (see Section 5) by up-to-
date widely used approach based on the Fourier series. In
this case, the periodic forcing term F(t), which exhibits
jump discontinuities, takes the form presented in Figure
15(a).
The 25th partial sum of the Fourier series has large os-
cillations near the jump, which decrease the maximum of
the partial sum above of the function itself. The over-
shoot does not die out as the number of frequency com-
ponents increases, but approaches a finite limit. This is
one of causes of insufficiency of the Fourier approach.
As a result, the Fourier series computations give the

Z. TRZASKA 141
variations in time of the system response x(t) which is
shown in Figure 15(b). Using the Fourier series ap-
proximations of both F(t) and x(t) we can present the
one-period energy loop on the energy phase plane in the
form presented in Figure 15(c). Thus, it is clear that
there are important discrepancies with respect to exact
results presented in Section 5.
Hysteresis energy loops are viable alternatives to ac-
tive, reactive, distortion and apparent powers. The pro-
posed method exhibits several advantages. Simulations
using one-period energy loops are exact and much faster
than Fourier series simulations.
0 12 3 45 6 7 8910
-20
0
20
40
60
80
100
120
140
time [s]
F(t) [kN]
Fouri er seri es repres entati on of F(t )
(a)
0 12 3 45 6 7 8910
-2
0
2
4
6
8
10
12
14
16 x 10
-3
time [ s]
x(t) [m]
Fourier series repres ent at i on of x (t )
(b)

Z. TRZASKA 142
-2 0 2 4 6810 12 14 16
x 10
-3
-20
0
20
40
60
80
100
120
140
x[m]
F(t) [kN]
Fourier s eri es repres ent ati on of one-period energy l oop
(c)
Figure 15. Results of the fourier series computations: (a) Forcing term exhibiting Gibbs effect; (b) Variations in time of the
system response; (c) Fourier series representation of the one-period energy loop.
8. Acknowledgements
The author would like to thank the anonymous reviewers
for their constructive comments.
REFERENCES
[1] J. Kisilowski and K. Knothe, “Advanced Railway Vehicle
Dynamics,” Technico-Scientific Publisher, Warsaw, 1991.
[2] J. Targosz, “Vibroisolation Systems in Railway and Auto-
motive Transportation Applications,” AGH University
Science & Technology Press, Cracow, 2007.
[3] G. Schupp, “Computational Bifurcation Analysis: An
Efficient Method for Studying Stationary and Periodic
Motions,” SIMPACK User Meeting, Eisenach, 9-11 No-
vember 2004, pp. 1-9.
[4] M. J. Steenbergen, “Modeling of Wheels and Rail Dis-
continuities in Dynamic Wheel-Rail Contact Analysis,”
Vehicle System Dynamics, Vol. 44, No. 10, 2006, pp.
763-787. doi:10.1080/00423110600648535
[5] J. Santamaria, E. G. Vadillo and J. Gomez, “Influence of
Creep Forces on the Risk of Derailment of Railway Vehi-
cles,” Vehicle System Dynamics, Vol. 47, No. 6, 2009, pp.
721-752. doi:10.1080/00423110802368817
[6] S. Iwnicki, “Handbook of Railway Vehicle Dynamics,”
Taylor & Francis, Boca Raton, 2006.
[7] O. D. I. Nwokah and Y. Hurmuzu, “The Mechanical Sys-
tems Design Handbook: Modeling, Measurements and
Control,” CRC Press, London, 2002.
[8] C. W. de Silva, “Vibrations. Fundamentals and Practice,”
CRC Press, London, 2000.
[9] H. Bachman, et al., “Vibration Problems in Structures,”
Birkhäuser-Verlag, Basel, 1995.
doi:10.1007/978-3-0348-9231-5
[10] H. Benaroua, “Mechanical Vibrations. Analysis, Uncer-
tain Control,” Marcel Dekker, New York, 2004.
[11] G. Schupp, C. Weidemann and L. Mauer, “Modeling the
Contact between Wheel and Rail within Multibody Sys-
tem Simulation,” Vehicle System Dynamics, Vol. 41, No.
5, 2004, pp. 349-364.
doi:10.1080/00423110412331300326
[12] J. Piotrowski and W. Kik, “A Simplified Model of
Wheel/Rail Contact Mechanics for Non-Hertzian Prob-
lems and Its Application in Rail Vehicle Dynamic Simu-
lations,” Vehicle System Dynamics, Vol. 46, No. 1-2,
2008, pp. 27-48. doi:10.1080/00423110701586444
[13] Y. Bezin, S. D. Iwnicki and M. Cavallett, “The Effect of
Dynamic Rail Roll on the Wheel-Rail Contact Condi-
tions,” Vehicle System Dynamics, Vol. 46, No. 1, 2008,
pp. 107-117. doi:10.1080/00423110701882348
[14] U. von Wagner, “Nonlinear Dynamic Behavior of a
Railway Wheelset,” Vehicle, System, Dynamics, Vol. 47,
No. 5, 2009, pp. 627-640.
doi:10.1080/00423110802331575
[15] A. Alonso and J. G. Giménez, “Non-Steady State Model-
ing of Wheel-Rail Contact Problem for the Dynamic
Simulation of Railway Vehicles,” Vehicle System Dy-
namics, Vol. 46, No. 3, 2008, pp. 179-196.
doi:10.1080/00423110701248011
[16] K. Zboinski and M. Dusza, “Bifurcation Approach to the
Influence of Rolling Radius Modeling and Rail Inclina-
tion on the Stability of Railway Vehicles in a Curved
Track,” Vehicle System Dynamics, Vol. 46, No. 1, 2008,

Z. TRZASKA 143
pp. 1023-1037. doi:10.1080/00423110802037255
[17] K. Knothe and S. Stichel, “Schienenfahrzeugdynamik,”
Springer, Berlin, 2007.
[18] R. P. Feynman, “There’s Plenty of Room at the Bottom:
An Invitation to Enter a New World of Physics,” Caltech
Engineering and Science, Vol. 23, No. 5, 1960, pp. 22-36.
http://www.zyvex.com/nanotech/feynman.html
[19] C. W. de Silva, “Vibration and Shock Handbook,” Taylor
& Francis, Boca Raton, 2005.
[20] K. E. Drexler, “Nanosystems: Molecular Machinery, Manu-
facturing, and Computation,” Wiley, New York, 1992.
[21] V. L. Popov, et al., “Friction Coefficient in ‘Rail-Wheel’-
Contacts as a Function of Material and Loading Parame-
ters,” Physical Mesomechanics, Vol. 5, No. 3, 2002, pp.
113-120.
[22] A. A. Shabanaa, K. E. Zaazaaa, J. L. Escalonab and J. R.
Sany, “Development of Elastic Force Model for Wheel/
Rail Contact Problems,” Journal of Sound and Vibrations,
Vol. 269, No. 1-2, 2004, pp. 295-325.
doi:10.1016/S0022-460X(03)00074-9
[23] R. von Schwerin, “Multibody System Simulation: Nu-
merical Methods, Algorithms, and Software,” Springer-
Verlag, Berlin, 1999.
[24] D. T. Greenwood, “Advanced Dynamics,” CUP, Cambridge,
2003.
[25] J. Misiak and S. Stachura, “Selected Problems of Static
Stability and Dynamics of Rod and Shell Structures,”
Publishing Office of the Warsaw University of Ecology
and Management, Warsaw, 2010.
[26] W. Blajer, “A Geometrical Interpretation and Uniform
Matrix Formulation of Multibody System Dynamics,”
Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 81, No. 4, 2001, pp. 247-259.
[27] A. Orlova, Y. Boronenko, H. Scheffel, R Fröhling and W.
Kik, “Tuning von Üterwagendrehgestellen Durch Rad-
satzkopplungen,” ZEV-Glasers Annalen, Vol. 126, No. 4,
2002, pp. 270-282.
[28] J. Evans and S. Iwnicki, “Vehicle Dynamics and the
Wheel Rail Interface,” 2002.
http://www.railtechnologyunit.com
[29] D. Karnopp, “Vehicle Stability,” Marcel Dekker Inc.,
New York, 2004. doi:10.1201/9780203913567
[30] Z. Trzaska and W. Marszalek, “Periodic Solutions of
DAEs with Applications to Dissipative Electric Circuits,”
Proceedings of the IASTED Conference Modeling, Identi-
fication and Control, Lanzarote, 6-8 February 2006, pp.
309-314.
[31] Z. Trzaska, “Straightforward Method for Studies of Peri-
odic Non-Harmonic States of Linear Systems,” Archive of
Electrical Engineering, Vol. 53, No. 2, 2004, pp. 191-
215.
[32] Z. Trzaska, “A New Approach to Shaping One-Period En-
ergies of Dynamical Systems Operating in Non-Sinu-
soidal States,” Archive of Electrical Engineering, Vol. 54,
No. 3, 2005, pp. 265-287.
[33] Z. Trzaska and W. Marszalek, “Computing Periodic So-
lutions of Linear Differential-Algebraic Systems with
Nonsinusoidal Excitations,” Archive of Electrical Engi-
neering, Vol. 55, No. 3-4, 2006, pp. 255-271.
[34] Z. Trzaska, “One-Period Energy in Dynamical Systems
with Periodic Discontinuous Excitations,” Elektronika,
Vol. 48, No. 3, 2007, pp. 26-32.
[35] E. Zerzm, “Topics in Multidimensional Linear Systems
Theory,” Springer, London, 2000.
[36] R. R. Borrelli and C. S. Colleman, “Differential Equa-
tions: A Modeling Perspective,” Wiley, New York, 2004.