Int. J. Communications, Network and System Sciences, 2010, 3, 483-487
doi:10.4236/ijcns.2010.35065 Published Online May 2010 (http://www.SciRP.org/journal/ijcns/)
Synchronization in Wireless Networks for Practical
MIMO-OFDM Systems
Muhammad Khurram Kiyani1, Muhammad Usman Ahmed2, Asim Loan1
1Department of Electrical Engineering, UET, Lahore, Pakistan
2Department of Computer Sciences, LUMS, Lahore, Pakistan
Received February 21, 2010; revised March 24, 2010; accepted April 25, 2010
Abstract
In this paper a frequency offset estimation technique for Wireless Local Area and Wireless Metropolitan Ar-
ea Networks is presented. For frequency offset estimation, we have applied a low-complexity frequency off-
set estimator for simple AWGN channels to fading channels for MIMO-OFDM systems. Simulation results
have shown that the performance of the proposed estimator is better than the low complexity frequency off-
set estimator designed for AWGN channels.
Keywords: Synchronization, Multiple Input Multiple Output, Orthogonal Frequency Division Multiplexing,
Wireless Local Area Networks, Wireless Metropolitan Area Networks, Stanford University
Interim Channels
1. Introduction
A lot of research has been carried out in carrier frequ-
ency offset estimation for Single Input Single Output
(SISO) Orthogonal Frequency Division Multiplexing
(OFDM) systems but comparatively less work has been
done in Multiple Input Multiple Output (MIMO) OFDM
systems. In [1], timing metric for frame synchronization
and frequency offset estimation in OFDM is proposed in
the downlink. In [2], a coarse timing synchronization is
carried out by using autocorrelation and then Carrier
Frequency Offset (CFO) is estimated by performing pre-
cise autocorrelation only on samples that have been
compensated for coarse timing synchronization. Both [1]
and [2] have sufficiently explored OFDM but they do not
incorporate MIMO. However, in [3], a novel frequency
synchronization scheme is presented which uses repeated
pseudo-noise training sequences to correct CFO in MI-
MO-OFDM systems. Also, in [4], integer CFO and
fractional CFO are estimated for MIMO-OFDM sys-
tems through special training sequences by solving
complex or real polynomial corresponding to the cost
function. Although both [3] and [4] have dovetailed
MIMO with OFDM systems but they lack the practical-
ity as they have not incorporated any particular standard.
In this paper we have extended the work of Luise &
Reggia- nnini (L & R), [5], by adapting their AWGN
single channel frequency estimator to multipath fading
channels using IEEE 802.16-2004 Standards [6], and
IEEE 802.11n Standards [7]. The technique used is
non-recursive as realistic MIMO scenarios entail chang-
ing channels with information being sent in bursts corre-
sponding to the duration of the coherence time of the
channel.
The remaining paper is organized as follows. Section 2
covers the details of system model. Section 3 gives the
description of the proposed frequency offset estimator
and Section 4 explains the results obtained through si-
mulations. Section 5 finally gives the conclusion.
2. System Model
A frequency offset can be introduced by relative motion
between the transmitter and the receiver (Doppler spread)
and by the inaccuracies in the Local Oscillator (LO).
Channel estimation in MIMO-OFDM system is very
sensitive to any frequency offset in the down converted
signal because frequency offset introduces a time depen-
dant factor that degrades the estimation of channel res-
ponse matrix H. Therefore accurate frequency offset es-
timation would result in a better channel estimate and a
more robust system.
Generally, a multipath fading channel is changing the-
refore the transmission is done in packets with the packet
length being governed by the coherence time of the
channel, i.e., the time for which the channel response

M. K. KIYANI ET AL. 484
does not change. In packet based communications, the
channel response matrix H must be estimated for each
packet. This is generally done by using a training se-
quence known to the receiver. We have used SUI Chan-
nels, [8], here as multipath fading channels and a pream-
ble specified in IEEE 802.16-2004 and IEEE 802.11n as
a training sequence for WMAN and WLAN respectively.
Our proposed algorithm estimates a constant frequency
offset over a length of symbols for every packet.
In MIMO, the signal received at each receiving ante-
nna is the superposition of the transmitted signals that
from different transmit antennas. Thus, the training signal
for each transmit antenna needs to be transmitted without
being interfered by the others. Figure 1 shows three
transmission patterns that avoid interfering with one an-
other: independent, scattered and orthogonal patterns. For
the sake of brevity we will only discuss the independent
pattern. The independent pattern transmits training signal
from one antenna at a time while the other antennas are
silent, thus guaranteeing orthogonality, in the time dom-
ain, between each training signal. The independent pattern
is often the most appropriate for MIMO-OFDM, since the
preamble is usually generated in the time domain.
To encode the training sequence we have used the in-
dependent pattern and assigned to each transmit antenna
a standard training sequence. This means that at a given
time only one transmit antenna is transmitting the train-
ing sequence as shown in Figure 2. We have also as-
sumed that the distance between transmitting antennas is
less than λ/2 and they all encounter the same channel
statistics.
3. Proposed Frequency Offset Estimation
Technique
The training sequence symbol is transmitted from the mth
transmit antenna and received on any of the receive an-
tenna. The kth sampling index of this received symbol
can be written as:
[
]
2
()()1.
mk
jvkT
rkhcenkforkN
πθ+
=+≤≤ (1)
In the above equation, hm denotes the complex channel
coefficient between the mth transmit antenna and a spe-
cific receive antenna, v is the frequency offset that needs
to be estimated and nk is the complex white Gaussian
noise with variance No.
In general, there would be multiple receive antennas and
each receive antenna would have a separate LO that
would introduce some frequency drift; this means that
frequency estimation needs to be done separately for
each receive antenna. The frequency offset v could pos-
sibly be different for different sub-carriers because Dop-
pler induced frequency shifts depend on the wavelength
of the transmission. Data modulation can be removed by
multiplying r(k) with ck*, because for PSK constellations
ck ck
* = 1 and the training sequence z(k) is known(The
training sequence symbols, taken from IEEE Standards
802.11n and 802.16, are assumed to be a Phase Shift
Keying (PSK) constellation such as Quadrature Phase
Shift Keying).
2
*
()()().
jvkT
zkrkchenk
m
k
πθ


+
=×=+ (2)
The autocorrelation of the z(k) sequence is defined as:
() () () ()
.
1
1,
1
N
Rz
pkkpforkpN
kp
Np z
∗
≡−≤≤ ∑
=
+−
(3)
Substituting (2) in (3) we get the following expression
for R(p):
Figure 1. Three different patterns for transmitting training signals in MIMO-OFDM systems [9].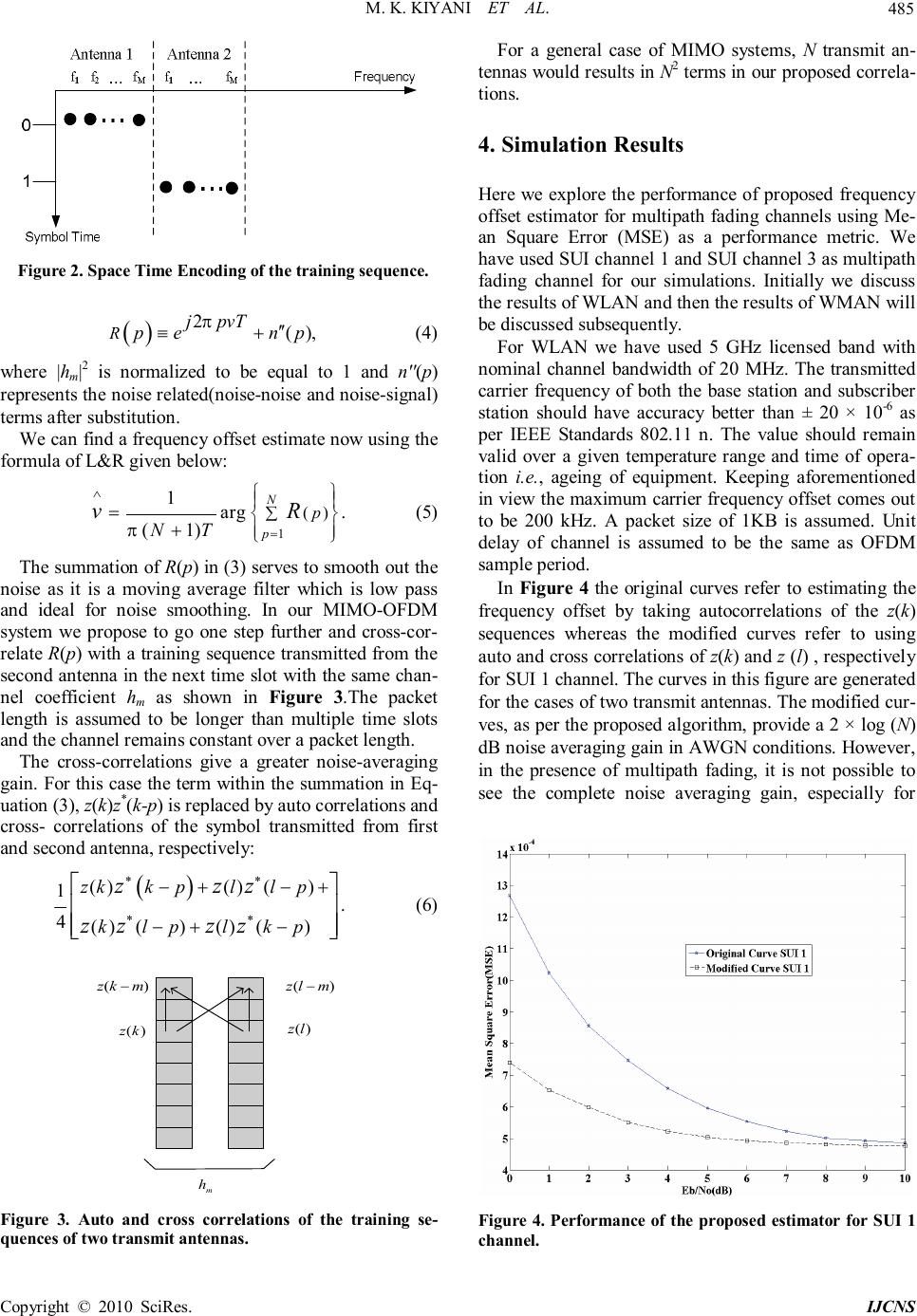

M. K. KIYANI ET AL.
485
Figure 2. Space Time Encoding of the training sequence.
()
2
(),
RjpvT
penp
π
′′
≡+ (4)
where |h
m
|
2
is normalized to be equal to 1 and n''(p)
represents the noise related(noise-noise and noise-signal)
terms after substitution.
We can find a frequency offset estimate now using the
formula of L&R given below:
1
()
1
arg.
(1)
N
p
p
NT
vR
π
∧
=


∑



=+ (5)
The summation of R(p ) in (3) serves to smooth out the
noise as it is a moving average filter which is low pass
and ideal for noise smoothing. In our MIMO-OFDM
system we propose to go one step further and cross-cor-
relate R(p) with a training sequence transmitted from the
second antenna in the next time slot with the same chan-
nel coefficient hm as shown in Figure 3.The packet
length is assumed to be longer than multiple time slots
and the channel remains constant over a packet length.
The cross-correlations give a greater noise-averaging
gain. For this case the term within the summation in Eq-
uation (3), z(k)z*(k-p ) is replaced by auto correlations and
cross- correlations of the symbol transmitted from first
and second antenna, respectively:
(
)
()()()
1
.
4()()()()
zkkpllp
klplkp
zzz
zzzz
∗∗
∗∗
−+−+
−+−




(6)
()
zk
()
zkm
−
()
zl
()
zlm
−
m
h
Figure 3. Auto and cross correlations of the training se-
quences of two transmit antennas.
For a general case of MIMO systems, N transmit an-
tennas would results in N2 terms in our proposed correla-
tions.
4. Simulation Results
Here we explore the performance of proposed frequency
offset estimator for multipath fading channels using Me-
an Square Error (MSE) as a performance metric. We
have used SUI channel 1 and SUI channel 3 as multipath
fading channel for our simulations. Initially we discuss
the results of WLAN and then the results of WMAN will
be discussed subsequently.
For WLAN we have used 5 GHz licensed band with
nominal channel bandwidth of 20 MHz. The transmitted
carrier frequency of both the base station and subscriber
station should have accuracy better than ± 20 × 10-6 as
per IEEE Standards 802.11 n. The value should remain
valid over a given temperature range and time of opera-
tion i.e., ageing of equipment. Keeping aforementioned
in view the maximum carrier frequency offset comes out
to be 200 kHz. A packet size of 1KB is assumed. Unit
delay of channel is assumed to be the same as OFDM
sample period.
In Figure 4 the original curves refer to estimating the
frequency offset by taking autocorrelations of the z(k)
sequences whereas the modified curves refer to using
auto and cross correlations of z(k) and z (l) , respectively
for SUI 1 channel. The curves in this figure are generated
for the cases of two transmit antennas. The modified cur-
ves, as per the proposed algorithm, provide a 2 × log (N)
dB noise averaging gain in AWGN conditions. However,
in the presence of multipath fading, it is not possible to
see the complete noise averaging gain, especially for
Figure 4. Performance of the proposed estimator for SUI 1
channel.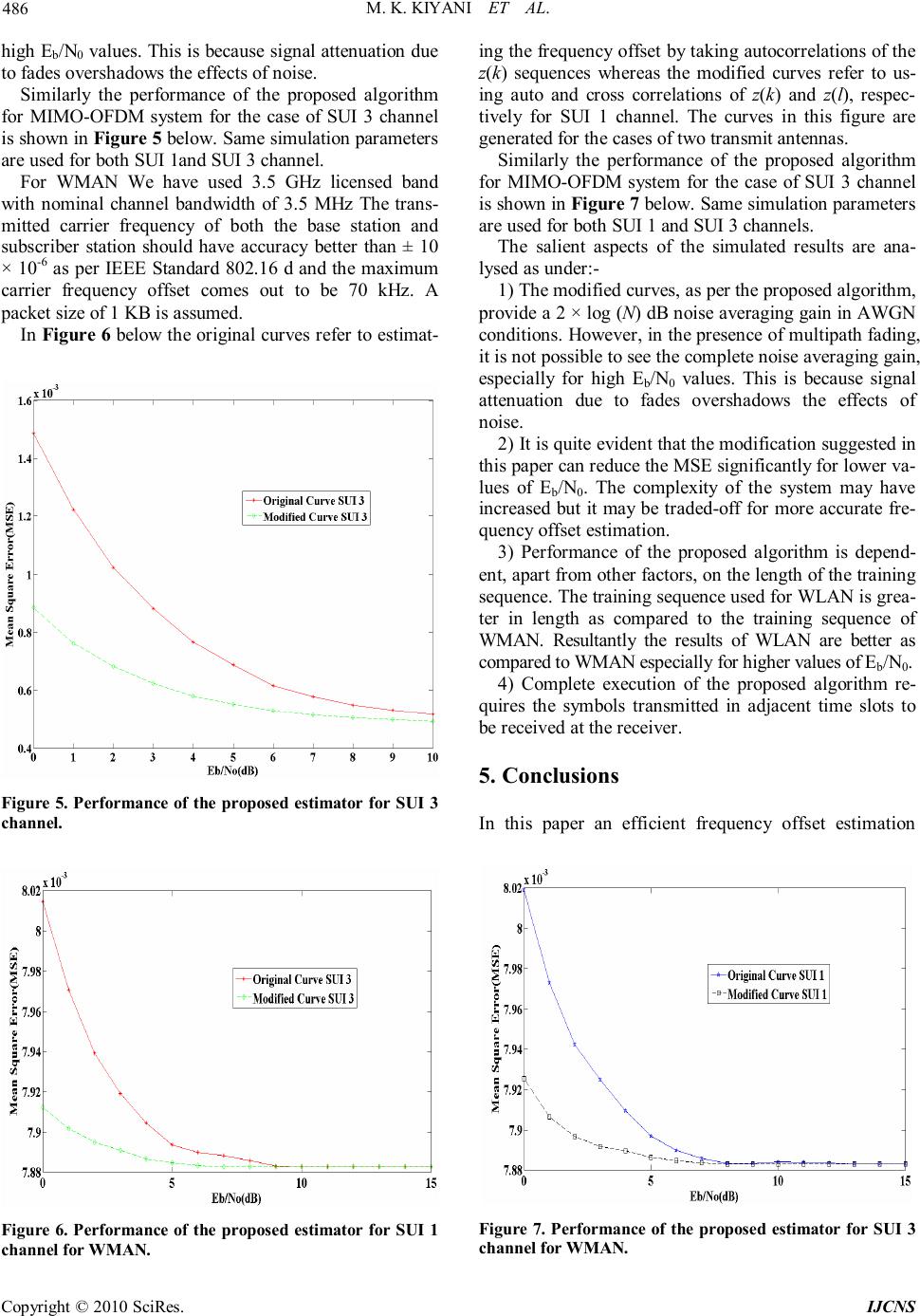

M. K. KIYANI ET AL. 486
high Eb/N0 values. This is because signal attenuation due
to fades overshadows the effects of noise.
Similarly the performance of the proposed algorithm
for MIMO-OFDM system for the case of SUI 3 channel
is shown in Figure 5 below. Same simulation parameters
are used for both SUI 1and SUI 3 channel.
For WMAN We have used 3.5 GHz licensed band
with nominal channel bandwidth of 3.5 MHz The trans-
mitted carrier frequency of both the base station and
subscriber station should have accuracy better than ± 10
× 10-6 as per IEEE Standard 802.16 d and the maximum
carrier frequency offset comes out to be 70 kHz. A
packet size of 1 KB is assumed.
In Figure 6 below the original curves refer to estimat-
Figure 5. Performance of the proposed estimator for SUI 3
channel.
Figure 6. Performance of the proposed estimator for SUI 1
channel for WMAN.
ing the frequency offset by taking autocorrelations of the
z(k) sequences whereas the modified curves refer to us-
ing auto and cross correlations of z(k) and z(l), respec-
tively for SUI 1 channel. The curves in this figure are
generated for the cases of two transmit antennas.
Similarly the performance of the proposed algorithm
for MIMO-OFDM system for the case of SUI 3 channel
is shown in Figure 7 below. Same simulation parameters
are used for both SUI 1 and SUI 3 channels.
The salient aspects of the simulated results are ana-
lysed as under:-
1) The modified curves, as per the proposed algorithm,
provide a 2 × log (N) dB noise averaging gain in AWGN
conditions. However, in the presence of multipath fading,
it is not possible to see the complete noise averaging gain,
especially for high Eb /N0 values. This is because signal
attenuation due to fades overshadows the effects of
noise.
2) It is quite evident that the modification suggested in
this paper can reduce the MSE significantly for lower va-
lues of Eb /N0. The complexity of the system may have
increased but it may be traded-off for more accurate fre-
quency offset estimation.
3) Performance of the proposed algorithm is depend-
ent, apart from other factors, on the length of the training
sequence. The training sequence used for WLAN is grea-
ter in length as compared to the training sequence of
WMAN. Resultantly the results of WLAN are better as
compared to WMAN especially for higher values of Eb/N0.
4) Complete execution of the proposed algorithm re-
quires the symbols transmitted in adjacent time slots to
be received at the receiver.
5. Conclusions
In this paper an efficient frequency offset estimation
Figure 7. Performance of the proposed estimator for SUI 3
channel for WMAN.

M. K. KIYANI ET AL.
487
technique for MIMO-OFDM systems in multipath envi-
ronment is presented. Simulation results have shown that
synchronization problems in MIMO-OFDM systems can
be solved with proposed algorithm which gives good
performance and tends to be limited only by multipath
fading. Since our extension of the simple L & R estima-
tor to the MIMO-OFDM case deals with data encoding
and not with the final estimation step, we have preserved
the optimality property of the L & R estimate.
6. References
[1] C. N. Kishore and V. U. Reddy, “A Frame Synchroniza-
tion and Frequency Offset Estimation Algorithm for
OFDM System and its Analysis,” EURASIP Journal on
Wireless Communications and Networking, Vol. 2006,
2006, pp. 1-16.
[2] T.-H. Kim and I.-C. Park, “Two Step Approach for
Coarse Time Synchronization and Frequency Offset Es-
timation for IEEE 802.16d Systems,” IEEE Workshop on
Signal Processing Systems, Shanghai, 17-19 October
2007, pp. 193-198.
[3] L.-M. He, “Carrier Frequency Offset Estimation in MI-
MO OFDM Systems,” 4th IEEE Conference on WiCOM,
Dalian, 12-14 October 2008, pp. 1-4.
[4] Y. X. Jiang, X. H. You, X. Q. Gao and H. Minn, “Train-
ing Aided Frequency Offset Estimation for MIMO
OFDM Systems via Polynomial Routing, ” 67th IEEE Ve-
hicular Technology Conference, Singapore, 11-14 May
2008.
[5] M. K. Kiyani, M. U. Ahmed and A. Loan, “Synchroniza-
tion in Fixed Broadband Wireless Access for Practical
MIMO OFDM systems,” 9th IEEE Malaysian Interna-
tional Conference on Communications, Kuala Lumpur,
15-17 December 2009.
[6] M. Luise and R. Reggiannini, “Carrier Frequency Recov-
ery in All-Digital Modems for Burst-Mode Transmis-
sions,” IEEE Transactions on Communications, Vol. 43,
No. 2-4, 1995, pp. 1169-1178.
[7] “IEEE P802.11n/D11.0 Draft Standard for Information
Technology, Telecommunications and Information Ex-
change between Systems,” Local and Metropolitan Area
Networks—Part 11: Wireless LAN Medium Access Con-
trol (MAC) and Physical Layer (PHY) Specifications,
2009.
[8] K. V. Erceg, S. Hari, M. S. Smith, D. S. Baum, et al.,
“Channel Models for Fixed Wireless Applications, ” IEE-
E 802.16.3 Task Group Contributions, 1 February 2001.
[9] G. J. Andrews, A. Ghosh and R. Muhamed, “Fundamen-
tals of WiMAX Understanding Broadband Wireless
Networking, ” Prentice Hall Communications Engineering
and Emerging Technologies Series, Prentice Hall, Febru-
ary, 2007.