J. Biomedical Science and Engineering, 2012, 5, 162-169 JBiSE
http://dx.doi.org/10.4236/jbise.2012.54021 Published Online April 2012 (http://www.SciRP.org/journal/jbise/)
Automatic determination of MS lesion subtypes based on
fractal analysis in brain MR images
Mahdi Mohamadkhanloo, Farzad Mehrabi, Abdolhamid Sohrabi
Department of Medical Science, Aja University, Tehran, Iran
Received 29 November 2011; revised 25 December 2011; accepted 29 January 2012
ABSTRACT
In this paper a novel approach based on fractal
analysis has been proposed to determine MS lesions
into two subtypes (i.e., Enhancing lesions (Acute), T1
“black holes” (chronic) lesions) in Fluid Attenuated
Inversion Recovery (FLAIR) MR images, automati-
cally. In the proposed method, firstly, MS lesion vox-
els are segmented in FLAIR images using Entropy-
Based EM Algorithm and Markov Random Field
(MRF) model. Then, Fractal dimension of each lesion
voxel is computed in FLAIR images and used with
signal intensity features (T1-weighted, gadolinium
enhanced T1-weighted, T2-weighted). Finally, a neu-
ral network classifier is applied to feature vectors.
Evaluation of the proposed method was performed by
manual segmentation of chronic and acute lesions in
gadolinium enhanced T1-weighted (Gad-E-T1-w)
images by studying T1-weighted (T1-w) and T2-
weighted (T2-w) images, using similarity criteria. The
results showed a good correlation between the lesions
segmented by the proposed method and by experts
manually. Thus, the suggested method is useful to
reduce the need for paramagnetic materials in con-
trast enhanced MR imaging which is a routine pro-
cedure for separation of acute and chronic lesions.
Keywords: Multiple Sclerosis; MRI; Fractal Dimension;
Lesion Subtype
1. INTRODUCTION
Multiple sclerosis (MS) is the commonest idiopathic in-
flammatory demyelinating disease of the central nervous
system that predominantly affects young adults about 30
years. It changes the morphology and structure of the
brain and in the most of case irreversible clinical disabi-
lity. Much MS research has focused on CNS immune
responses because a specific cause for MS has not been
identified. One of the most important modalities of me-
dical imaging that assist in the diagnosis and monitoring
of MS is MRI. Recently, the study of MRI in MS has
been flourishing in the field of research due to its ability
in generating multiple images of the same tissue with
different contrast mechanisms using different image ac-
quisition protocols and parameters. In its application to
MS, macroscopic areas of damage or loss of myelin with
hyper or hypo intensities relative to the surrounding tis-
sues are shown by MRI. Different MRI protocols in-
cluding T1-weighted (T1-w), T2-weighted (T2-w), PD-
weighted (PD-w), and fluid-attenuated inversion reco-
very (FLAIR) T2 images are being investigated for im-
proving the performance in the early inflammatory stage
and in the advanced stage of the diseases [1]. Figure 1
shows a slice of a multi-parametric MRI of two MS pa-
tients. The lesions appear as regions with increased sig-
nal intensity on the T2-w and FLAIR images and de-
creased signal intensity (hypointense) on the T1-w image.
There are two major categories of lesions which can be
identified with conventional MR imaging: acute lesions
demonstrating blood-brain barrier leakage on contrast-
enhanced MR imaging (enhancing lesions), chronic se-
verely damaged lesions that are hypointense, so-called
“black holes” on T1-w MR images [2]. Acute plaques
appear with less signal changes in T1-w images due to
more inflammation, edema, and little demyelination. The
borders of acute plaques in T1-w images are vague and
cannot be marginate well because they compared with
white matter, will be Signal sointense or hypointense
(less darkness). Gradually, the plaques become darker in
T1-w images with progress in demyelination process and
also chronicity of the disease. The lesions Borders be-
come sharper with more demyelination and gliosis (re-
placement of fibrous tissue instead of myelin and neuron)
As a result of this process some chronic plaques become
darker known as black holes. The signal intensity of
these plaques will not change in enhanced T1-w images
(by injection of the paramagnet contrast materials) and
they will appear as hyperintense areas in T2-w images
[3]. Ying Wu et al. [2], proposes Intensity-based statisti-
cal k-nearest neighbor (k-NN) classification has com-
bined with template-driven segmentation and partial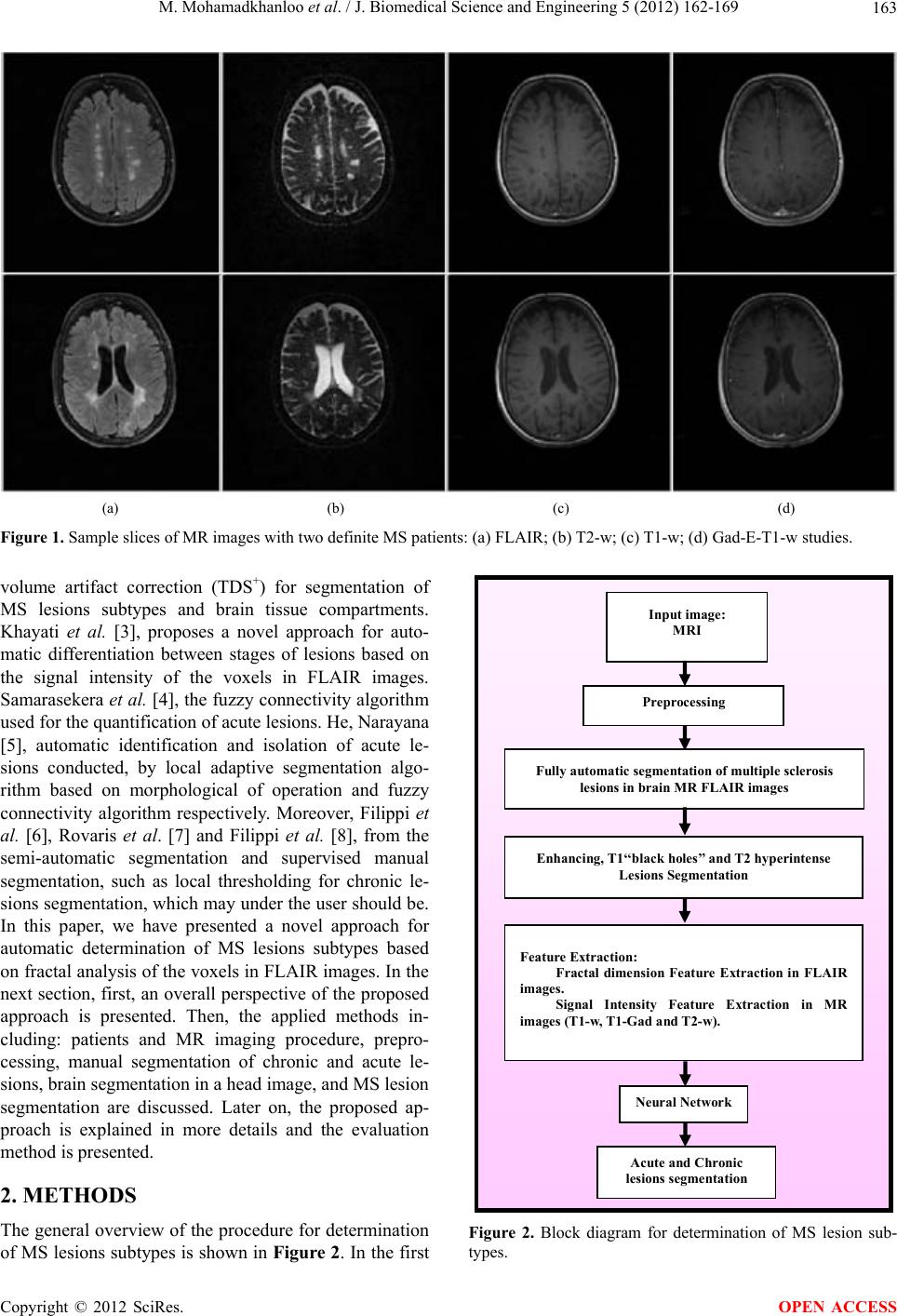

M. Mohamadkhanloo et al. / J. Biomedical Science and Engineering 5 (2012) 162-169 163
(a) (b) (c) (d)
Figure 1. Sample slices of MR images with two definite MS patients: (a) FLAIR; (b) T2-w; (c) T1-w; (d) Gad-E-T1-w studies.
volume artifact correction (TDS+) for segmentation of
MS lesions subtypes and brain tissue compartments.
Khayati et al. [3], proposes a novel approach for auto-
matic differentiation between stages of lesions based on
the signal intensity of the voxels in FLAIR images.
Samarasekera et al. [4], the fuzzy connectivity algorithm
used for the quantification of acute lesions. He, Narayana
[5], automatic identification and isolation of acute le-
sions conducted, by local adaptive segmentation algo-
rithm based on morphological of operation and fuzzy
connectivity algorithm respectively. Moreover, Filippi et
al. [6], Rovaris et al. [7] and Filippi et al. [8], from the
semi-automatic segmentation and supervised manual
segmentation, such as local thresholding for chronic le-
sions segmentation, which may under the user should be.
In this paper, we have presented a novel approach for
automatic determination of MS lesions subtypes based
on fractal analysis of the voxels in FLAIR images. In the
next section, first, an overall perspective of the proposed
approach is presented. Then, the applied methods in-
cluding: patients and MR imaging procedure, prepro-
cessing, manual segmentation of chronic and acute le-
sions, brain segmentation in a head image, and MS lesion
segmentation are discussed. Later on, the proposed ap-
proach is explained in more details and the evaluation
method is presented.
2. METHODS
The general overview of the procedure for determination
of MS lesions subtypes is shown in Figure 2. In the first
Inp ut i m ag e:
MRI
Preprocessing
Enhancing, T1‘‘black holes’’ and T2 hyperintense
Lesions Segmentation
Feature Extraction:
Fractal dimension Feature Extraction in FLAIR
images.
Signal Intensity Feature Extraction in MR
images (T1-w, T1-Gad and T2-w).
Fully automatic se gmentation of multiple sclerosis
lesions in brain MR FLAI R images
Neural Network
Acute and Chronic
lesions segme ntation
Figure 2. Block diagram for determination of MS lesion sub-
types.

M. Mohamadkhanloo et al. / J. Biomedical Science and Engineering 5 (2012) 162-169 164
phase of the proposed method, pre-processing and nor-
malization of raw magnetic resonance images is desired.
Then, the lesions are extracted from normal tissue and
cerebrospinal fluid (CSF) in the FLAIR images. Then, a
binary mask is generated from the lesions class, resulted
from previous step and applied to the original slices
(T1-w, T1-Gad and T2-w) to extract the lesions. Also,
fractal dimension of segmented lesions in FLAIR images
are computed locally and used along with intensity fea-
tures. The input dataset and it’s desired output containing
lesions subtypes which were manually prepared by a
neurologist (acute and chronic) are used to train the neu-
ral network.
Finally, determination of MS lesions subtypes in MR
images are done using the Neural Network classifier and
is evaluated by comparing the obtained results with the
manual determination.
2.1. Patients and MR Imaging
The proposed method is evaluated on a dataset which is
obtained and used in [9]. This dataset contains 16 female
and 4 male with average age of 29 ± 8 years old, this
dataset is selected according to the revised Mc Donald
criteria 2005 [10]. All images were acquired according to
full field MRI criteria of MS [10] in T2-weighted (T2-w),
T1-weighted (T1-w), Gadolinium enhanced T1-weighted
and FLAIR in axial, sagittal and coronal surfaces. We
selected the FLAIR images, especially axial ones, with
lesions in deep, priventricular, subcortical, and cortical
white matters (supratentorial lesions). More lesion load
and higher accuracy of FLAIR in revealing of these MS
lesions were the reason for this selection [11]. Each im-
age volume (patient data) consisted of averagely 40
slices with a 256 × 256 scan matrix. The pixel size was 1
mm2, and the slice thickness was 3 mm without any
gap.
2.2. Preprocessing
As mentioned before, after segmentation of MS lesions
in Flair images, a binary mask containing lesion class is
applied to the original slices (T1-w, T1-Gad and T2-w) to
extract the lesions intensities. So, as the primary step, all
slices and all the examinations are registered using SPM
software.
2.3. Manual Segmentation of Chronic and Acute
Lesions
There are two complimentary methods to separate acute
and chronic (black holes) lesions: the first is the observa-
tion of GD-enhanced lesions for acute ones and the se-
cond is the observation of serial T1-w, T2-w, and Gad-
E-T1-w slices in different times (imaging follow-up
study) for chronic ones. In the second method, lesions
which have not been enhanced and repeated in serial
T1-w images are recognized as black holes. The seg-
mentation of MS lesion subtypes was performed manu-
ally by neurologist and radiologist in Flair images with
visual inspection of corresponding T1-w, Gad-E-T1-w
and T2-w images. Lesions which have not been en-
hanced and repeated in serial T1-w images are recog-
nized as chronic “black holes” and lesions which have
been enhanced and repeated in serial Gad-E-T1-w im-
ages are recognized as acute.
In this study, a neurologist and a radiologist, who were
not aware of the results of the computerized methods in
this research, were asked to perform manual segmenta-
tion of MS lesions in FLAIR images and also, chronic
and acute lesions in corresponding Gad-E-T1-w slices.
The results of this step for all the selected slices (learning
and test) provided binary segmented images, were used
as Gold standard [12] to evaluate the performance of
proposed method.
2.4. Brain and Lesions Segmentation
The brain segmentation was performed using a fully
automatic object-oriented approach [13]. This method
was based on the regional-spatial characteristics of brain
in MR images. At first, original image is converted to a
binary image. Then, morphological opening on the bi-
nary image is performed and tiny regions are eliminated.
Three rectangular masks showing the cerebral regions
are produced and the regions in the binary image which
have overlap with these rectangles are preserved and, the
rest are eliminated. Final mask is generated by dilation of
selected regions and filling tiny holes. Finally, an image,
which includes only cerebral tissues, is obtained by
applying the resulted mask on the original image. Then,
MS lesions are segmented in FLAIR images using a fully
automatic method which is based on entropy based EM
algorithm and Markov random field model [14]. This
method estimates a gaussian mixture model with three
kernels as cerebrospinal fluid (CSF), normal tissue and
Multiple Sclerosis lesions. To estimate this model, an
automatic Entropy based EM algorithm was used to find
the best estimated Model. Then, Markov random field
(MRF) model and EM algorithm were utilized to obtain
and upgrade the class conditional probability density
function and the apriori probability of each class. After
estimation of Model parameters and apriori probability,
brain tissues were classified using Bayesian classifica-
tion.
Then, a binary mask is generated from the lesions
class, resulted from previous step and applied to the re-
gistered original slices (T1-w, T1-Gad and T2-w) to
extract the lesions. The result of this step, Provides Sig-

M. Mohamadkhanloo et al. / J. Biomedical Science and Engineering 5 (2012) 162-169 165
nal intensity feature vectors.
3. FRACTAL DIMENSION FEATURE
The concept of fractal is first proposed by Mandelbrot
[15] to describe the complex geometry of the objects in
nature. Fractal dimension (FD) is a real number that de-
scribes the fractal property of the object. There are sev-
eral different methods to estimate the FD.
Estimating fractal dimension from frequency domain
is an application of Fourier power spectrum. This method
is extendable and is very accurate potentially in terms of
calculation. Furthermore, it’s calculation based on defi-
nite mathematical relations is one of the advantages of
this method. Due to above mentioned reasons and the
good experimental results, this method was used to esti-
mate fractal dimension in the paper. In this method, the
power spectrum (p(u,v)) of an ideal fractal two-dimen-
sional image (f(x,y)) with fractal dimension (fd) is defined
as follows:


222
,;
H
puv crru v

 (3.1)
where c is a constant, H is Hurst coefficient, v and u are
frequency variables. If the two-dimensional power spec-
trum of an image is shown as S(r,θ) in Polar coordinates,
S(r,θ) could be considered as an one-dimensional func-
tion

s
r

for every θ direction

s
r

. Analysis
shows the power spectrum behavior for a constant value
θ, and could be used to investigate some characteristics
such as existence of energy peaks in radiant direction
from start. A comprehensive statement for power spec-
trum is obtained summing these functions [16]:
 
π
0
s
rs

 
r (3.2)
So, the slope of Least Squares Linear Regression of
logarithmic graph S(r) in terms of r equals –2H. Fractal
dimension of the image then can be obtained from equa-
tion:
1
dd
f
tH (3.3)
where d is topological dimension, which equals 3 for
surface. It should be mentioned that estimating the fractal
dimension is done excluding DC component from S. For
a homogenous texture, most energy is concentrated in
low frequencies, H has high value, therefore d
t
f
is
small. Whereas, for a heterogeneous texture with vast
spectrum, H has low value, therefore d
f
is big.
For each pixel which belongs to lesion class, we have
computed fractal dimension locally through a n × n win-
dow. Computing fractal dimension using a window with
big size will be time consuming. Also, small size causes
erroneous results. So, we have considered a 16 × 16
window to compute fractal dimension, locally.
According to the experimental results, we observed
that Lesions and normal tissue categories have a fractal
dimension in 2.1 < fd < 2.6 and 2.3 < fd < 3, respectively.
But there is a little overlap between these two areas
which make us not to be able to classify acute lesions
from chronic lesions.
4. CLASSIFICATION OF ACUTE AND
CHRONIC LESIONS
Multilayer perceptron (MLP) is employed to classify
acute lesions from chronic lesions. After Registration of
MRI images (T1-w, T1-Gad and T2-w) and segmentation
of MS lesions in FLAIR images, fractal dimension is
computed for each pixel locally and used with MRI sig-
nal intensities (T1-w, T1-Gad and T2-w) as feature vec-
tors.
The classifier is constructed using a three-layer MLP
consisting of an input layer, a hidden layer and an output
layer. The input layer has a number of nodes equal to the
input vector length. The output layer consists of one node,
accounting for a possibility of only 2 classes to be classi-
fied. Also, the number of nodes in the hidden layer is 20,
which this number selected by trial and error method.
This number of nodes in hidden layer makes best result
for classification. Both input and output nodes use linear
transfer functions, and the hidden layer uses a sigmoid
function. The epochs in the data set were randomly di-
vided into two sets: a Training Set and a Testing Set.
70% of the epochs are used to train the MLP while 30%
were used to test the performance of the classifier. This
process was done for 100 times to reach the average ac-
curacy. The MLP was trained using the Back propagation
strategy, and the termination criteria are the completion
of 2000 training epochs or reaching a mean square error
level of 0.01 for the training data set.
5. EVALUATION
The result of the chronic lesions classification based on
fractal analysis method is compared with the gold stan-
dard. The similarity criteria, SI [17], overlap fraction (OF)
and extra fraction (EF) [18], are calculated for the all
selected (learning and test) slices. The SI is a criterion
for the correctly classified chronic lesions area relative to
the total area of chronic lesions in both the gold standard
and the area of the segmented image. The OF and EF
specify, respectively, the areas which have been correctly
and falsely classified as chronic lesions areas relative to
the chronic lesions area in the gold standard. The simi-
larity criteria are defined by the Eq.5 (5.1-5.3)
2TP
SI 2TPFPFN

 (5.1)
TP
OF TPFN  (5.2)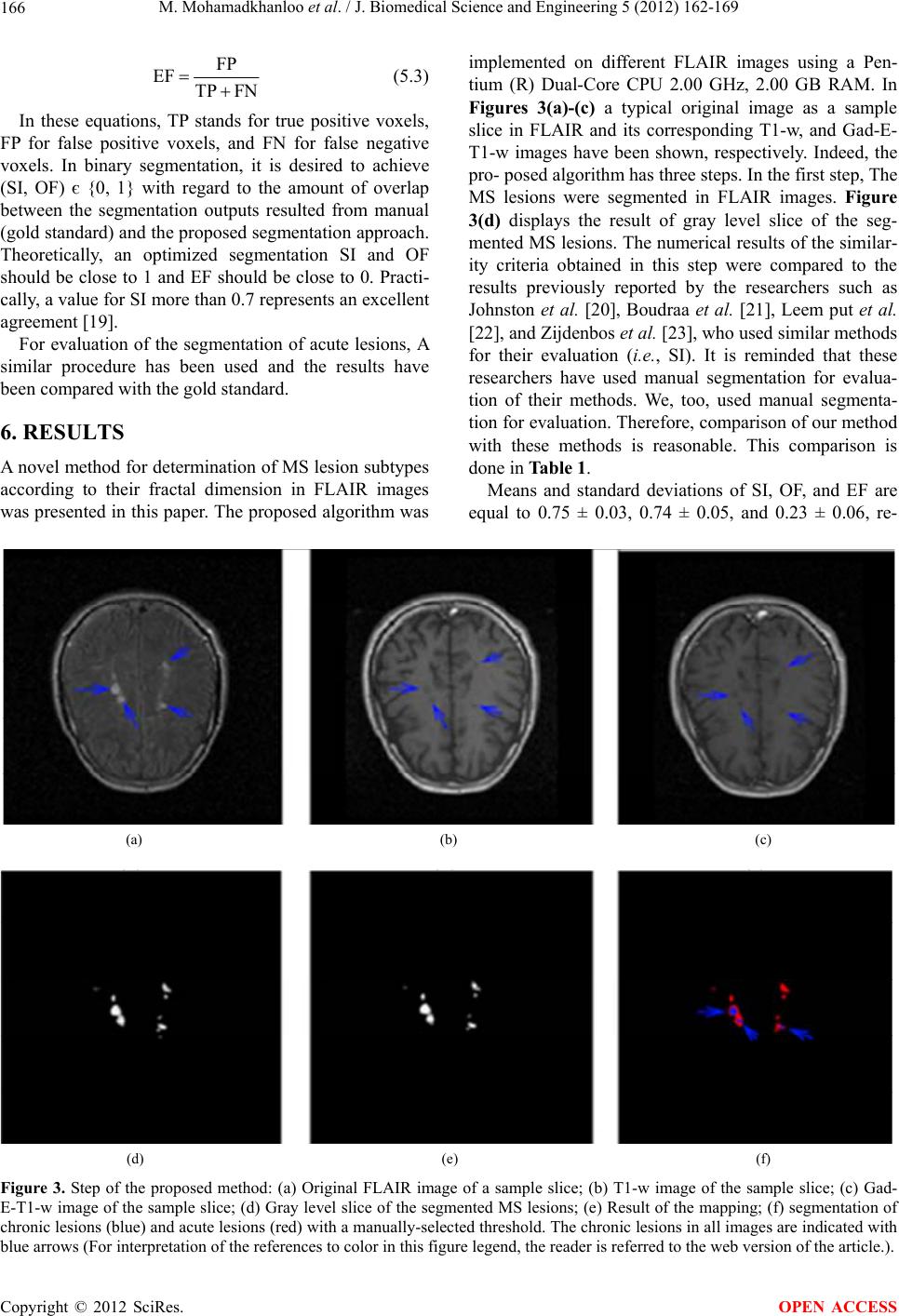

M. Mohamadkhanloo et al. / J. Biomedical Science and Engineering 5 (2012) 162-169 166
implemented on different FLAIR images using a Pen-
tium (R) Dual-Core CPU 2.00 GHz, 2.00 GB RAM. In
Figures 3(a)-(c) a typical original image as a sample
slice in FLAIR and its corresponding T1-w, and Gad-E-
T1-w images have been shown, respectively. Indeed, the
pro- posed algorithm has three steps. In the first step, The
MS lesions were segmented in FLAIR images. Figure
3(d) displays the result of gray level slice of the seg-
mented MS lesions. The numerical results of the similar-
ity criteria obtained in this step were compared to the
results previously reported by the researchers such as
Johnston et al. [20], Boudraa et al. [21], Leem put et al.
[22], and Zijdenbos et al. [23], who used similar methods
for their evaluation (i.e., SI). It is reminded that these
researchers have used manual segmentation for evalua-
tion of their methods. We, too, used manual segmenta-
tion for evaluation. Therefore, comparison of our method
with these methods is reasonable. This comparison is
done in Table 1.
FP
EF TP FN  (5.3)
In these equations, TP stands for true positive voxels,
FP for false positive voxels, and FN for false negative
voxels. In binary segmentation, it is desired to achieve
(SI, OF) є {0, 1} with regard to the amount of overlap
between the segmentation outputs resulted from manual
(gold standard) and the proposed segmentation approach.
Theoretically, an optimized segmentation SI and OF
should be close to 1 and EF should be close to 0. Practi-
cally, a value for SI more than 0.7 represents an excellent
agreement [19].
For evaluation of the segmentation of acute lesions, A
similar procedure has been used and the results have
been compared with the gold standard.
6. RESULTS
A novel method for determination of MS lesion subtypes
according to their fractal dimension in FLAIR images
was presented in this paper. The proposed algorithm was
Means and standard deviations of SI, OF, and EF are
equal to 0.75 ± 0.03, 0.74 ± 0.05, and 0.23 ± 0.06, re-
(a) (b) (c)
(d) (e) (f)
Figure 3. Step of the proposed method: (a) Original FLAIR image of a sample slice; (b) T1-w image of the sample slice; (c) Gad-
E-T1-w image of the sample slice; (d) Gray level slice of the segmented MS lesions; (e) Result of the mapping; (f) segmentation of
chronic lesions (blue) and acute lesions (red) with a manually-selected threshold. The chronic lesions in all images are indicated with
blue arrows (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.).

M. Mohamadkhanloo et al. / J. Biomedical Science and Engineering 5 (2012) 162-169 167
Table 1. The SI values of MS lesions, segmented by different method.
Method Johnson et al. [20] Boudraa et al. [21] Leemput et al. [22] Zijdenbos et al. [23] approach Fully automatic
Similarity Index 0.65 0.62 0.51

0.68

0.75
Figure 4. Comparison of a binary segmented image (Seg) with
the reference image (Ref). TP, TN, FP, and FN represent true
positive, true negatives, false positives, and false negatives
voxels, respectively [12].
spectively. These values show a better performance of
MS (FLAIR) lesions segmentation for all the selected
slices, as mentioned in the evaluation step. For classifi-
cation of chronic and acute lesions using the method, the
defined mapping was calculated and applied to the gray
level slices of the lesions. The result of the mapping has
been shown in Figure 3(e). Also, for each lesion pixel in
Flair image, fractal dimension is computed locally and is
considered as a feature. The result of voxel classification
into two stages: chronic and acute by applying a manu-
ally-selected threshold has been shown in Figure 3(f).
As it can be seen, one of the chronic lesions is missed.
The computed total volume for the chronic lesions (i.e.,
0.165 cc) is much less than the value of true total volume
(i.e., 0.37 cc).
Using the Eq.5 (5 .1-5.3) , means of the similarity crite-
ria were computed for the learning slices (see the first
row in Ta bl e 2 ). It is recalled, that the value of SI more
than 0.7 is considered as an excellent segmentation [19].
In the evaluation step, classification was performed for
the test slices, then, the means and standard deviations of
the similarity criteria were computed and showed in the
second row of Table 2.
The means of the calculated similarity criteria for the
test slices compared to the learning slices decreased
about 6% and 4% for SI and OF, respectively, and in-
creased about 3% for EF criterion. In spite of a decrease
(a) (b)
(c) (d)
Figure 5. Segmentation of the chronic lesions (blue) and the
acute lesions (red) in the sample slice: (a) Gad-E-T1-w image
of the sample slice; (b) Segmentation by the manually-selected
threshold; (c) Segmentation based on fractal analysis method,
(d) Segmentation based on signal intensity method. The chronic
lesions in all images are indicated with blue arrows (For inter-
pretation of the references to color in this figure legend, the
reader is referred to the web version of the article.).
in the SI value for the test slices, as this value is still
higher than 0.7, the performance of the proposed algo-
rithm is acceptable [19]. A comparison between the ef-
fects of the fractal dimension and signal intensity fea-
tures is shown in Figure 5. In this Figures 5(a)-(c) rep-
resent the Gad-ET1-w image of the sample slice, seg-
mentation of the chronic lesions for manually-selected
threshold, and segmentation based on fractal analysis
method, respectively. The chronic lesions in the all im-
ages are indicated with blue arrows. As it is seen, for the
fractal dimension value, all of the chronic lesions have
been detected properly. The computed total volume of
the chronic lesions (i.e., 0.35 cc) is very close to that of
the true volume (i.e., 0.37 cc).
As it was mentioned before, these acute lesions have
not been enhanced because of low value of blood brain
barrier destruction or relative inactivity of the lesion that
leads the lesion toward to chronicity. For comparison of
the results of the based on fractal analysis method for
segmentation of the chronic and the acute lesions, the

M. Mohamadkhanloo et al. / J. Biomedical Science and Engineering 5 (2012) 162-169 168
Table 2. Means and standard deviation of the similarity criteria for based on fractal and without fractal methods.
Slices SI (with fractal) SI (without fractal) OF (with fractal) OF (without fractal)EF(with fractal) EF (without fractal)
Learning 0.83 ± 0.07 0.84 ± 0.03 0.92 ± 0.03 0.9 ± 0.02 0.23 ± 0.04 0.30 ± 0.05
Test 0.77 ± 0.04 0.74 ± 0.05 0.88 ± 0.06 0.85 ± 0.05 0.28 ± 0.07 0.33 ± 0.06
based on intensity method was reapplied to the result of
the mapping with the threshold preset automatically to
0.58. Then, the means and standard deviations of the
similarity criteria were computed again for the all Se-
lected slices (learning and test) (see Table 2). As it is
seen in this table, the means of the calculated.
Similarity criteria for the test slices compared to
learning Slices decreased about 10% and 5% for SI and
OF, respectively, and increased about 5% for EF. Like,
the based on fractal analysis method, there are trivial
differences between learning and test slices. In Figure
5(d), the result of the chronic lesion segmentation per-
formed by the based on intensity method has been shown.
As it is seen, all chronic lesions have been detected cor-
rectly. The computed total volume of the chronic lesions
(i.e., 0.345 cc) is very close to that of the true volume
(i.e., 0.37 cc).
We selected based on fractal method as the reference
method for segmentation of the chronic and acute lesions
due to good accuracy according to Table 2 and low com-
putational complexity, where, SI, Similarity Index; OF,
Overlap Fraction; and EF, Extra Fraction.
REFERENCES
[1] Mortazavi, D., Kouzani, A.Z. and Soltanian-Zadeh, H.
(2011) Segmentation of multiple sclerosis lesions in MR
images: A review. Diagnostic Neuroradiology, 54, 299-
320. doi:10.1007/s00234-011-0886-7
[2] Wu, Y., Warfield, S.K., Tan, I.L., Wells, W.M. III, Meier,
D.S., van Schijndel, R.A., Barkhof, F. and Guttmann, C.R.
(2006) Automated segmentation of multiple sclerosis le-
sion subtypes with multichannel MRI. NeuroImage, 32,
1205-1215. doi:10.1016/j.neuroimage.2006.04.211
[3] Khayati, R., Vafadust, M., Towhidkhah, F. and Nabavi,
S.M. (2007) A novel method for automatic determination
of different stages of multiple sclerosis lesions in brain
MR FLAIR images. Computerized Medical Imaging and
Graphics, 32, 124-133.
doi:10.1016/j.compmedimag.2007.10.003
[4] Samarasekera, S., Udupa, J.K., Miki, Y., Wei, L. and
Grossman, R.I. (1997) A new computer-assisted method
for the quantification of enhancing lesions in multiple
sclerosis. Journal of Computer Assisted Tomography, 21,
145-151. doi:10.1097/ 000 04728- 1997010 00-000 28
[5] He, R. and Narayana, P.A. (2002) Automatic delineation
of Gd enhancements on magnetic resonance images in
multiple sclerosis. Medical Physics, 29, 1536-1546.
doi:10.1118/1.1487422
[6] Filippi, M., Rovaris, M., Campi, A., Pereira, C. and Comi,
G. (1996) Semiautomated thresholding technique for meas-
uring lesion volumes in multiple sclerosis: Effects of the
change of the threshold on the computed lesion loads.
Acta Neurologica Scandinavica, 93, 30-34.
doi:10.1111/j.1600-0404.1996.tb00166.x
[7] Rovaris, M., Filippi, M., Calori, G., et al. (1997) Intra-
observer reproducibility in measuring new putative MR
markers of demyelination and axonal loss in multiple
sclerosis: A comparison with conventional T2-weighted
images. Journal of Neurology, 244, 266-270.
doi:10.1007/s004150050083
[8] Filippi, M., Horsfield, M.A., Hajnal, J.V., et al. (1996)
Quantitative assessment of magnetic resonance imaging
lesion load in multiple sclerosis. Journal of Neurology,
Neurosurgery & Psychiatry, 64, S88-S93.
doi:10.1093/brain/119.4.1349
[9] Khayati, R., Vafadust, M., Towhidkhah, F. and Nabavi,
S.M. (2008) Fully automatic segmentation of multiple
sclerosis lesions in brain MR FLAIR images using adap-
tive mixtures method and markov random field model.
Computers in Biology and Medicine, 38, 379-390.
doi:10.1016/j.compbiomed.2007.12.005
[10] Polman, C.H., Reingold, S.C., Edan, G., Fillippi, M.,
Hartung, H.P. and Kappos, L. (2005) Diagnostic criteria
for MS 2005 revisions to the MC Donald criteria. Annals
of Neurology, 58, 840-846. doi:10.1002/ana.20703
[11] Edelman, R.R., Hesselink, J.R., Zlatkin, M.B. and Crues,
J.V. (2006) Clinical magnetic resonance imaging. 3rd
Edition, Saunders, Philadelphia, 1571-1615.
[12] Anbeek, P., Vincken, K.L., van Osch, M.J.P., Bisschops,
R.H.C. and van der Grond, J. (2004) Probabilistic seg-
mentation of white matter lesions in MR imaging. Neuro
Image, 21, 1037-1044.
doi:10.1016/j.neuroimage.2003.10.012
[13] Khayati, R. (2006) Quantification of multiple sclerosis
lesions based on fractal analysis. Ph.D. Thesis, Amirkabir
University of Technology, Tehran.
[14] Bijar, A., Khanloo, M.M., Benavent, A.P. and Khayati, R.
(2011) Segmentation of MS lesions using entropy-based
EM algorithm and Markov random fields. Journal of
Biomedical Science and Engineering, 4, 552-561.
doi:10.4236/jbise.2011.48071
[15] Mandelbrot, B.B. and Freeman, W.H. (1983) The fractal
geometry of nature, San Francisco, 1982. No. of pages:
460. Earth Surface Processes and Landforms, 8, 406.
doi:10.1002/esp.3290080415
[16] Gonzalez, R.C., Woods, R.E. and Eddins, S.L. (2002)
Digital Image Processing Using Matlab, Pearson Prentice
Hall, Upper Saddle River. doi:10.1117/1.3115362
[17] Zijdenbos, A.P., Dawant, B.M., Margolin, R.A. and Pal-

M. Mohamadkhanloo et al. / J. Biomedical Science and Engineering 5 (2012) 162-169 169
mer, A.C. (1994) Morphometric analysis of white matter
lesions in MR images: Method and validation. IEEE
Transactions on Medical Imaging, 13, 716-724.
doi:10.1109/42.363096
[18] Stokking, R., Vincken, K.L. and Viergever, M.A. (2000)
Automatic morphology based brain segmentation (MB-
RASE) from MRI-T1 data. NeuroImage, 12, 726-738.
doi:10.1006/nimg.2000.0661
[19] Bartko, J.J. (1991) Measurement and reliability: Statisti-
cal thinking considerations. Schizophrenia Bulletin, 17,
483-489. doi:10.1093/schbul/17.3.483
[20] Johnston, B., Atkins, M.S., Mackiewich, B. and Ander-
son, M. (1996) Segmentation of multiple sclerosis lesions
in intensity corrected multispectral MRI. IEEE Transac-
tions on Medical Imaging, 15, 154-169.
doi:10.1109/42.491417
[21] Boudraa, A.O., Dehakb, S.M.R., Zhu, Y.M., Pachai, C.,
Bao, Y.G. and Grimaud, J. (2000) Automated segmenta-
tion of multiple sclerosis lesions in multispectral MR
imaging using fuzzy clustering. Computers in Biology
and Medicine, 30, 23-40.
doi:10.1016/S0010-4825(99)00019-0
[22] Leemput, K.V., Maes, F., Vandermeulen, D., Colchester,
A. and Suetens, P. (2001) Automated segmentation of
multiple sclerosis lesions by model outlier detection.
IEEE Transactions on Medical Imaging, 20, 677-688.
doi:10.1109/42.938237
[23] Zijdenbos, A.P., Forghani, R. and Evans, A.C. (2002)
Automatic pipeline analysis of 3-D MRI data for clinical
trials: Application to multiple sclerosis, IEEE Transac-
tions on Medical Imaging, 21, 1280-1291.
doi:10.1109/TMI.2002.806283