Int. J. Communications, Network and System Sciences, 2010, 3, 462-465
doi:10.4236/ijcns.2010.35061 Published Online May 2010 (http://www.SciRP.org/journal/ijcns/)
Microstrip Low-Pass Elliptic Filter Design Based on
Implicit Space Mapping Optimization
Saeed Tavakoli, Mahdieh Zeinadini, Shahram Mohanna
Faculty of Electrical and Computer Engineering, the University of Sistan and Baluchestan, Zahedan, Iran
Received February 21, 2010; revised March 27, 2010; accepted April 28, 2010
Abstract
It is a time-consuming and often iterative procedure to determine design parameters based on fine, accurate
but expensive, models. To decrease the number of fine model evaluations, space mapping techniques may be
employed. In this approach, it is assumed both fine model and coarse, fast but inaccurate, one are available.
First, the coarse model is optimized to obtain design parameters satisfying design objectives. Next, auxiliary
parameters are calibrated to match coarse and fine models’ responses. Then, the improved coarse model is
re-optimized to obtain new design parameters. The design procedure is stopped when a satisfactory solution
is reached. In this paper, an implicit space mapping method is used to design a microstrip low-pass elliptic
filter. Simulation results show that only two fine model evaluations are sufficient to get satisfactory results.
Keywords: Implicit Space Mapping Optimization, Microstrip Low-Pass Elliptic Filter, Surrogate Model
1. Introduction
Considering the development of computer-aided design
methods, optimization has become a widely used tech-
nique in design of microwave circuits. A typical design
problem is to choose the design parameters to get the
desired response. The space mapping (SM), introduced
in [1], is a powerful technique to optimize complex mod-
els. The aim of this technique is to make a shortcut using
a cheaper but less accurate model, coarse model, to gain
information about the optimal parameter setting of the
expensive but accurate model, fine model. To obtain the
optimal design for the fine model, the SM establishes a
mapping between the parameters of the two models it-
eratively [1,2]. In some cases, this mapping is not ex-
plicit and it is hidden in the coarse model. The implicit
space mapping (ISM) [3], described below, addresses
this issue.
First, the coarse model is optimized to obtain design
parameters satisfying the design objectives. Second, an
auxiliary set of parameters in the coarse model, which
always remain fixed in the fine model, is calibrated to
match coarse and fine models’ responses. This step is
known as the parameter extraction step. Examples of the
auxiliary parameters are physical parameters, such as
relative dielectric constant, and geometrical parameters,
such as substrate height. The coarse model with updated
values of auxiliary parameters is known as the surrogate,
calibrated coarse, model. Considering the re-calibrated
auxiliary parameters fixed, then, the calibrated coarse
model is re-optimized to obtain a new set of design pa-
rameters. These design parameters are given to the fine
model to evaluate its performance [4]. The design pro-
cedure is stopped when a satisfactory solution is reached.
In this paper, an optimization procedure based on ISM
technique is applied to a microstrip low-pass elliptic fil-
ter. Agilent ADS and ADS Momentum [5] are employed
to simulate coarse and fine models, respectively.
2. Implicit Space Mapping Approach
The design objective is to calculate an optimal solution
for the fine model, as follows
 
arg min
f
fff
x
x
Rx 
 (1)
where

is a suitable objective function. The fine
model’s response,
f
R, is, for example, 11 S at selected
frequency points.
f
x

is the optimal fine model pa-
rameters to be determined. It can be found using the fol-
lowing iterative procedure


1arg min,
f
kK
fsf
x
xRxp 
 (2)
where
s
R refers to the surrogate model’s response. To

S. TAVAKOLI ET AL. 463
solve Equation (1), a two-step procedure is employed. In
the first step, the auxiliary parameters are calibrated so
that the surrogate and fine models’ responses become
similar enough. The auxiliary parameters are calculated
using the following equation
 
arg min,
kKK
ff sf
P
pRxRxp
(3)
where 0 p refers to the initial auxiliary parameters.
Cons ider in g the re-calibrated auxiliary parameters fixed,
then, the new surrogate model is re-optimized to obtain a
new set of design parameters, new
f
x
, in the second step.
If the fine model’s response for this new set of design
parameters satisfies the design specifications, the algo-
rithm is stopped. Otherwise, it re-calculates the auxiliary
parameters for the current design parameters [4,6].
3. Microstrip Low-Pass Elliptic Filter
Low-pass filters are components, which are used to elim-
inate unwanted harmonics. Low-pass elliptic filters can
provide a fairly sharp cut-off frequency [7]. In this paper,
ISM technique is applied to the optimization problem of
a low-pass elliptic filter with a cut-off frequency of 7
GHz. The structure of this filter is illustrated in Figure 1.
The coarse model is composed of empirical models of
simple microstrip elements, as shown in Figure 2. The
design specifications are as follows:
L
1
L
7
W
3
W
1
W
1
W
2
W
4
L
1
L
1
L
1
L
2
L
1
L
8
L
1
L
1
L
4
L
1
L
1
L
6
L
1
L
3
L
3
L
1
L
2
L
1
L
1
L
5
L
1
L
1
L
1
Figure 1. Microstrip low-pass elliptic filter structure.
MLOC
TL30
Subst="MSub4"
MLIN
TL6
Subst="MSub4"
MLIN
TL26
Subst="MSub4"
MLIN
TL4
Subst="MSub1"
MLIN
TL27
Subst="MSub1"
MLIN
TL25
Subst="MSub4"
MTEE
Tee3
Subst="MSub1"
MLIN
TL5
Subst="MSub4"
MLOC
TL29
Subst="MSub3"
MLIN
TL3
Subst="MSub3"
MLIN
TL23
Mod=Kirschning
Subst="MSub3"
MLIN
TL24
Subst="MSub4"
MTEE
Tee2
MLIN
TL22
Subst="MSub3"
MLIN
TL2
MLIN
TL21
Subst="MSub3"
MLOC
TL28
Subst="MSub2"
MLIN
TL11
Subst="MSub2"
MLIN
TL16
Subst="MSub2"
MTEE
Tee1
MLIN
TL17
Subst="MSub2"
MLIN
TL7
Subst="MSub2"
MTEE
Tee4
Subst="MSub2"
MLIN
TL18
Subst="MSub2"
MLIN
TL19
Subst="MSub2"
MLIN
TL8
Subst="MSub2"
MLOC
TL31
Subst="MSub2"
MLIN
TL20
Subst="MSub1"
MLIN
TL1
Subst="MSub1"
Term
Term2
Z=50 Ohm
Num=2
Term
Term1
Z=50 Ohm
Num=1
Subst="MSub3"
MLIN
TL24
Subst="MSub4"
Mod=Kirschning
Subst="MSub3"
MTEE
Tee2
Figure 2. Coarse model simulated by ADS.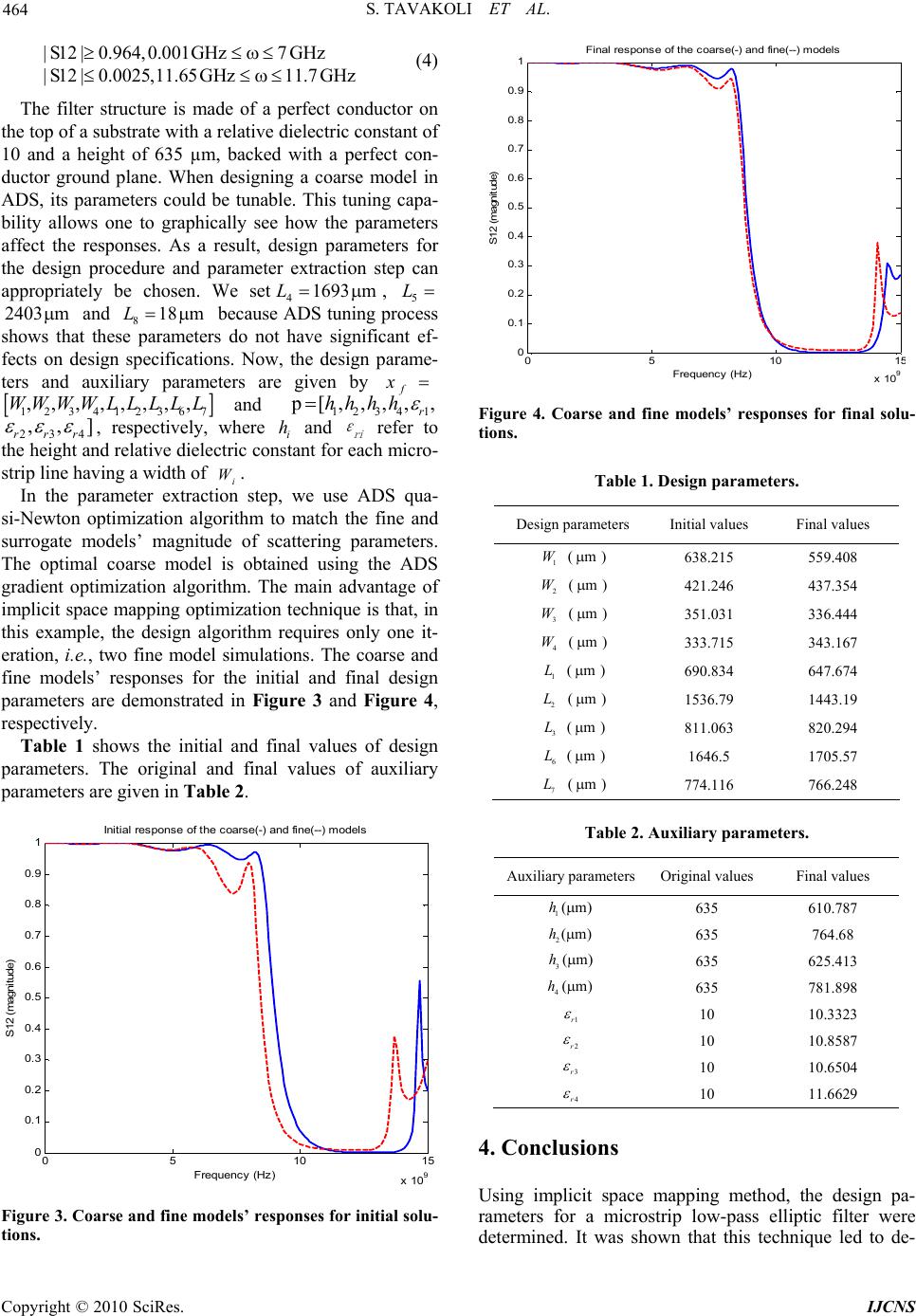

S. TAVAKOLI ET AL. 464
|S12 |0.964,0.001GHz7 GHz
|S12 |0.0025,11.65GHz11.7 GHz


(4)
The filter structure is made of a perfect conductor on
the top of a substrate with a relative dielectric constant of
10 and a height of 635 µm, backed with a perfect con-
ductor ground plane. When designing a coarse model in
ADS, its parameters could be tunable. This tuning capa-
bility allows one to graphically see how the parameters
affect the responses. As a result, design parameters for
the design procedure and parameter extraction step can
appropriately be chosen. We set41693 mL, 5
L

2403 m

and 818 mL because ADS tuning process
shows that these parameters do not have significant ef-
fects on design specifications. Now, the design parame-
ters and auxiliary parameters are given by f
x



123412367
,,,,,,,,WWWWL LLLLand 1234 1
p
[, ,, ,,
r
hhhh


234
,,]
rrr

 , respectively, where i h and
ri
ε refer to
the height and relative dielectric constant for each micro-
strip line having a width of i
W.
In the parameter extraction step, we use ADS qua-
si-Newton optimization algorithm to match the fine and
surrogate models’ magnitude of scattering parameters.
The optimal coarse model is obtained using the ADS
gradient optimization algorithm. The main advantage of
implicit space mapping optimization technique is that, in
this example, the design algorithm requires only one it-
eration, i.e., two fine model simulations. The coarse and
fine models’ responses for the initial and final design
parameters are demonstrated in Figure 3 and Figure 4,
respectively.
Table 1 shows the initial and final values of design
parameters. The original and final values of auxiliary
parameters are given in Table 2.
05 10 1
5
x 10
9
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Frequency (Hz)
S12 (magnitude)
Initial response of the coarse(-) and fine(--) models
Figure 3. Coarse and fine models’ responses for initial solu-
tions.
05 10 1
5
x 10
9
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Frequency (Hz)
S12 (magnitude
)
Final response of the coarse(-) and fine(--) models
Figure 4. Coarse and fine models’ responses for final solu-
tions.
Table 1. Design parameters.
Design parameters Initial values Final values
1
W (
m

) 638.215 559.408
2
W (
m

) 421.246 437.354
3
W (
m

) 351.031 336.444
4
W (
m

) 333.715 343.167
1
L
(
m

) 690.834 647.674
2
L
(
m

) 1536.79 1443.19
3
L
(
m

) 811.063 820.294
6
L
(
m

) 1646.5 1705.57
7
L
(
m

) 774.116 766.248
Table 2. Auxiliary parameters.
Auxiliary parametersOriginal values Final values
1(m)h

635 610.787
2(m)h

635 764.68
3(m)h

635 625.413
4(m)h 635 781.898
1r

10 10.3323
2r

10 10.8587
3r

10 10.6504
4r

10 11.6629
4. Conclusions
Using implicit space mapping method, the design pa-
rameters for a microstrip low-pass elliptic filter were
determined. It was shown that this technique led to de-

S. TAVAKOLI ET AL. 465
creasing the number of fine model evaluations. First, the
coarse model was optimized to obtain design parameters
satisfying the design objective. Second, auxiliary pa-
rameters were calibrated in the coarse model to match
coarse and fine models’ responses. Third, the improved
coarse model was re-optimized to obtain a new set of
design parameters. Finally, the resulting design parame-
ters were given to the fine model to evaluate its per-
formance. The design procedure was repeated by the
time a satisfactory solution was obtained. Simulation
results showed that only two evaluations of the fine
model were sufficient to get satisfactory results for the
given case-study application.
5. References
[1] J. W. Bandler, R. M. Biernacki, S. H. Chen, P. A. Grobe-
lny and R. H. Hemmers, “Space Mapping Technique for
Electromagnetic Optimization,” IEEE Transactions on
Microwave Theory and Techniques, Vol. 42, No. 12,
1994, pp. 2536-2544,.
[2] J. W. Bandler, Q. S. Cheng, S. A. Dakroury, A. S. Moh-
amed, M. H. Bakr, K. Madsen and J. Søndergaard,
“Space Mapping: the State of the Art,” IEEE Transac-
tions on Microwave Theory and Techniques, Vol. 52, No.
1, 2004, pp. 337-361.
[3] J. W. Bandler, Q. S. Cheng, N. K. Nikolova and M. A.
Ismail, “Implicit Space Mapping Optimization Exploiting
Preassigned Parameters,” IEEE Transactions on Microw-
ave Theory and Techniques, Vol. 52, No. 1, 2004, pp.
378-385.
[4] S. Koziel, Q. S. Cheng and J. W. Bandler, “Space
Mapping,” IEEE Microwave Magazine, Vol. 9, No. 6,
December 2008, pp. 105-122.
[5] “Agilent Advanced Design System (ADS),” Ver. 2008A,
Agilent Technologies, Santa Rosa, CA, 2008.
[6] J. W. Bandler, Q. S. Cheng, D. H. Gebre-Mariam, K. Ma-
dsen, F. Pedersen and J. Søndergaard, “EM-based Sur-
Rogate Modeling and Design Exploiting Implicit, Fre-
quency and Output Space Mappings,” IEEE MTT-S Inter-
national Microwave Symposium Digest, Philadelphia,
2003, pp. 1003-1006.
[7] M. C. V. Ahumada, J. Martel and F. Medina, “Design of
Compact Low-Pass Elliptic Filters Using Double-Sided
MIC Technology,” IEEE Transactions on Microwave
Theory and Techniques, Vol. 55, No. 1, January 2007, pp.
121-127.