Int. J. Communications, Network and System Sciences, 2010, 3, 446-452
doi:10.4236/ijcns.2010.35059 Published Online May 2010 (http://www.SciRP.org/journal/ijcns/)
Analysis and Comparison of Time Replica and Time
Linear Interpolation for Pilot Aided Channel
Estimation in OFDM Systems
Donglin Wang
Department of Electrical and Computer Engineering, University of Calgary, Calgary, Canada
Received March 10, 2010; revised April 11, 2010; accepted May 12, 2010
Abstract
This paper analyzes and compares two time interpolators, i.e., time replica and time linear interpolator, for
pilot aided channel estimation in orthogonal frequency division multiplexing (OFDM) systems. The mean
square error (MSE) of two interpolators is theoretically derived for the general case. The equally spaced pilot
arrangement is proposed as a special platform for these two time interpolators. Based on this proposed plat-
form, the MSE of two time interpolators at the virtual pilot tones is derived analytically; moreover, the MSE
of per channel estimator at the entire OFDM symbol based on per time interpolator is also derived. The ef-
fectiveness of the theoretical analysis is demonstrated by numerical simulation in both the time-invariant
frequency-selective channel and the time varying frequency-selective channel.
Keywords: OFDM, Channel Estimation, Time Replica, Time Linear Interpolation, Virtual Pilots
1. Introduction
Orthogonal frequency division multiplexing (OFDM)
[1-3] has been widely used in high-speed wireless com-
munication systems, such as broadband wireless local
area networks (WLANs) [4], wireless metropolitan area
networks (WMANs) [5] and worldwide interoperability
for microwave access (WIMAX) [6], due to its advan-
tages of transforming frequency-selective fading chan-
nels into a set of parallel flat fading sub-channels and
eliminating inter-symbol interference [7].
Channel estimation is one of the most essential tasks
in compensating distortion from channels and perform-
ing coherent detection in OFDM systems. Estimation is
usually performed by using pilot tones [8, 9] and is based
on inserting known pilot tones in each OFDM symbol,
where interpolation in time-frequency grid [10] plays an
important role in the estimation process. The usage of
virtual pilot tones [11-13] and time interpolation can
reduce the redundancy and guarantee a higher transmis-
sion bit rate. Among time interpolation methods, time
replica [14, 15] is widely used in time-invariant or slow
time-varying channel, which is simple to implement and
also efficient for subcarrier usage; time linear interpola-
tion [16-18] is widely used in slow or fast time-varying
channel, because it is simple to realize and usually can
give a satisfactory performance. However, some inter-
esting questions are raised as follows: 1) what kind of
time-varying channel is slow enough to utilize time rep-
lica? 2) Conversely, what kind of time-varying channel is
so fast that we have to employ time linear interpolation
instead of time replica? And 3) how much does time lin-
ear interpolation perform better than time replica by for a
time-invariant channel?
To answer these questions above, this paper analyzes
and compares the performances of time replica and time
linear interpolator in both the time-invariant frequency-
selective channel and the time varying frequency-selec-
tive channel. The MSE of both time interpolators is theo-
retically derived for the general cases. The equal spaced
pilot arrangement is employed as a special platform for
both time interpolators, where the positions of virtual
pilot tones in one OFDM symbol correspond to those of
pilot tones of its last and next OFDM symbols. Channel
state information (CSI) [19] at pilot tones is estimated by
least square (LS) estimator. CSI at virtual pilot tones in
one OFDM symbol is obtained by either of time interpo-
lators, where time replica is to completely replicate the
CSI at pilot tones of its last OFDM symbol while time
linear interpolator is to linearly interpolate values by
using the estimated CSI at the corresponding pilot tones
of both its last and next OFDM symbols. CSI at data

D. L. WANG
447
tones is finally obtained by frequency linear interpolation
[20].
This paper is organized as follows. In Section 2, the
MSEs of two interpolators, i.e. , time replica and time
linear interpolation, are theoretically derived for the gen-
eral case. In Section 3, the equally spaced pilot arrange-
ment is proposed as a special platform for analyzing
these two time interpolators. In Section 4, based on the
proposed platform, the MSE of two time interpolators at
the virtual pilot tones is derived analytically; moreover,
the MSE of channel estimators at the entire OFDM
symbol based on these two time interpolators is also de-
rived, respectively. Numerical results are reports in Sec-
tion 5, followed by conclusion in Section 6.
Notation:
2
g
denotes the modulus.
2
g
is the
2-norm operation.
{
}
k
E
g
is the expectation operation
on k.
{
}
,kl
E
g
means the expectation on both k and l.
{
}
k
Var
g
means the variance on k. ,
()
mimj
k
−+
δ denotes
the variation of the CSI of the
th
k
tone from the
(
)
th
mi
− OFDM symbol to the
(
)
th
mj
+ OFDM
symbol.
()
m
k
δ denotes the variation of the CSI of the
th
k
tone from the
th
m
OFDM symbol to the
(
)
1th
m+ OFDM symbol.
(
)
R
m
ek
and
(
)
L
m
ek
are the
channel estimation errors of the
th
m
OFDM symbol at
the
th
k
tone where time replica or time linear interpo-
lation are employed for CSI estimation at the virtual pilot
tones, respectively.
2. MSE of Two Time Interpolators
Assume that each OFDM symbol has N subcarriers
where pilots occupy P subcarriers. Denote the set of pilot
tones by
P
I
. By LS estimation, the CSI at pilot tones in
the
th
m
OFDM symbol can be obtained as
()
ˆ()
()
m
mm
Yk
Hk
Xk
= (1)
where
()
m
Xk
and
()
m
Yk
are the transmitted and re-
ceived pilots of the
th
m
OFDM symbol, respectively.
Assuming the pilot tones
()1
m
Xk
=
for convenience of
analysis, we have
ˆ
()()()
mmm
HkHkWk
=+ (2)
where
()
m
Hk
represents the true value and
()
m
Wk
is
a complex-valued sample of additive white Gaussian
noise (AWGN) process at the
th
m
OFDM symbol,
(
)
2
()~0,
m
WkCN
σ
.
Assuming that along the time axis in Figure 1, the da-
ta tones in the
th
m
OFDM symbol correspond to the
pilot tones in both the
(
)
th
mp− and the
(
)
th
mq+
OFDM symbol, the CSI at the data tones in the
th
m
OFDM symbol can be obtained by time interpolation by
using the estimated CSI at the pilot tones of both the
(
)
th
mp−and the
(
)
th
mq+ OFDM symbol, which is
thus called the virtual pilot tones. Denote the set of vir-
tual tones by
PP
I
. In this section, we will analyze and
compare the MSE performance of two time interpolators:
time replica and time linear interpolator.
2.1. Time Replica
Time replica at the virtual pilot tones in the
th
m
sym-
bol is to replicate the CSI at the pilot tones in the
(
)
th
mp− symbol,
ˆ ˆ
()(),
mmpPP
HkHkkI
−
=∈. (3)
By (2) and (3), the estimation error of time replica at
the
th
k
tone can be expressed as
-
--
ˆ
()()-()
()-()().
R
mmpm
mpmmp
ek Hk Hk
Hk Hk Wk
=
=+
(4)
The MSE using time replica can thus be obtained as
{
}
{
}
{ }
22
2
-
22
,
()()-()
().
R
Rkmkmpm
kmpm
EekEHk Hk
Ek
−
==+
=+
ξσ
δσ
(5)
2.2. Time Linear Interpolation
However, if using time linear interpolation, the estimated
CSI can be obtained as follows,
-
ˆ ˆˆ
()()()
mmpmq
pq
HkHkHk
p qp q+
=+
++
(6)
for
PP
kI
∈. By (2) and (6), the estimation error of time
linear interpolation at the
th
k
tone can be expressed as
( )
( )
--
()()-()()
()-()().
L
mmpmmp
mqmmq
pq
ekHk HkWk
p qp q
pq
Hk HkWk
p qp q
++
=+
++
=+
++
(7)
Figure 1. The virtual pilot tones in the
th
m
OFDM sym-
bol are time-interpolated by using the pilot tones at both
the
(
)
th
−mp and the
(
)
th
+mq OFDM symbol.

D. L. WANG 448
Based on (7), the MSE of time linear interpolation can
thus be obtained as
{
}
( )
2
222
,,
2
2
()
()()
.
L
Lkm
mpmmmq
k
Eek
pkqk pq
Ep qp qp q
−+
=

+ 
=−+

++ +


ξ
δδ
σ
(8)
2.3. Comparison
Subtracting (8) from (6), the difference between
R
ξ
and
L
ξ
can be expressed as
{
}
( )
2
2
,2
2
,,
2
()
()()
.
RLkmpm
mpmmmq
k
pq
Ek
p q
pkqk
Ep qp q
−
−+
−=+
+


−−

++


ξξδσ
δδ (9)
From (9), one can conclude that
1) In a time-invariant frequency-selective channel,
L
ξ
is always lower than
R
ξ
by
( )
2
10log 2
p q
pq
+dB; while
in a time-variant frequency-selective channel, the per-
formance comparison depends on the specific channel
variation;
2) Considering a real-valued channel variation, in low
noise environment, when ,,
()()0
mpmmmq
kk
−+
<
δδ and
,,
()()
mmqmpm
kk
+−
>δδ,
RL
<
ξξ
;
3) Considering a real-valued channel variation, in
noisy environment, when ,,
()()0
mpmmmq
kk
−+
≥
δδ or
,,
()()0
mpmmmq
kk
−+
<
δδ but ,,
()()
mmqmpm
kk
+−
<δδ ,
RL
>
ξξ
.
3. Special Case: Pilot Arrangement and
Channel Estimators
Assume that each OFDM symbol has N subcarriers
where pilots occupy P subcarriers and virtual pilots su-
perimposed with data samples also occupy P subcarriers.
Figure 2 shows the proposed pilot arrangement as a
platform, which is a special case but not loss of general-
ity, where along frequency axis, the pilot spacing is 2L
and the spacing between pilot and adjacent virtual pilot is
L. From Figure 2, one can see that along time axis, the
pilot spacing is 2 and the spacing between pilot and ad-
jacent virtual pilot is 1. Also, by LS estimation, the CSI
at pilot tones can be obtained by (1).
3.1. Time Interpolation at Virtual Pilot Tones
Denote the set of virtual tones by
PP
I
. The CSI at vir-
Figure 2. The proposed pilot arrangement as a special plat-
form, where the pilot tones in one OFDM symbol correspond
to the virtual pilot tones in its adjacent OFDM symbol.
tual pilot tones is obtained by time interpolation. In this
special pilot arrangement, since the virtual pilot tones at
the
th
m
symbol corresponds to the pilot tones at the
(
)
1th
m− symbol, time replica at the virtual pilot tones
in one symbol is to replicate the CSI at the pilot tones of
its last symbol,
-1
ˆ ˆ
()(),
mmPP
HkHkkI
=∈
. (10)
On the other hand, if using time linear interpolation,
we can get
-11
ˆˆ
()()
ˆ(),
2
mm
mPP
HkHk
HkkI
+
+
=∈
. (11)
3.2. Frequency Interpolation at Data Tones
Denote the set of data tones as
D
I
. Using frequency
linear interpolation [20], the CSI at the whole OFDM
symbol can be expressed as
( )
( )
ˆ ˆ
()()
1122
ˆ()
ˆ
()
121.
mm
m
m
Lll
HkHkL
LL
whenkLP
Hkl
Hk
whenkLP
−
++



≤≤+−
+=



=+−

(12)
where ()
D
klI
+∈
,
PPP
kII
∈∪ ,
11
lL
≤≤−
. Note
that the CSI for data tones located on the right side be-
yond the
(
)
1th
PL+ pilot/virtual pilot tone is decided
by the edge interpolation.
4. Performance Analysis for the Special Case
This section analyzes the performance of this special
case in terms of the MSEs of time interpolators and the
MSEs of the corresponding channel estimators.

D. L. WANG
449
4.1. MSE of Time Interpolators
For this special case, the MSE of time replica in (5) be-
comes
{
}
2
2
1
().
Rkm
Ek
−
=+
ξδσ
(13)
On the other hand, the MSE of time linear interpola-
tion in (8) becomes
2
2
1()()
.
2
mm
Lk kk
E
−

−

=+



δδ
ξσ
(14)
So, based on (13) and (14), the difference between
R
ξ
and
L
ξ
can be obtained as follows,
{ }
2
221
1()()
1
().
22
mm
RLkmk
kk
EkE
−
−

−

−=+−



δδ
ξξδσ
(15)
And, from (15), one can conclude that 1) in a time-
invariant frequency-selective channel,
L
ξ
is always
lower than
R
ξ
by 3 dB; in a time-variant frequency-
selective channel, the performance difference depends on
the specific channel variation; 2) in most situations, as
the general case in (9),
RL
>
ξξ
, i.e., time linear inter-
polation is better than time replica.
4.2. MSE of Channel Estimation
4.2.1. Time Replica
By LS estimation on pilot tones, time replica on virtual
pilot tones and frequency interpolation on data tones, the
corresponding MSE of channel estimation can be ex-
pressed as
2
,
LRLPRRF
PPNP
NNN
−
=++
ξξξξ
(16)
where
P
ξ
is the MSE of LS estimation and
RF
ξ
is the
MSE of frequency interpolation when using time replica
at virtual pilot tones.
As an average of both odd and even OFDM symbols,
except for the right side
(
)
1
L
−
tones using the edge
interpolation, a half of other data tones with the index
(
)
D
klI
+∈
have
P
kI
∈
while
(
)
PP
kLI
+∈ for fre-
quency linear interpolation; for the remaining data tones,
PP
kI
∈ while
(
)
P
klI
+∈
for frequency linear inter-
polation. Hence, using (12), we can get
RF
ξ
in (17),
where
()()()()
Fmmm
Lll
eklHkHkLHkl
LL
−
+=++−+
,
PPP
kII
∈∪ ,
(
)
1122
kLP
≤≤+−
, and
(1(2-1))
F
e LP l
++
(1(2-1))-(1(2-1))
mm
H LP H LP l
=+++
, are the inher-
ent errors by frequency interpolation,
F
ξ
is the inherent
MSE of frequency interpolation.
By substituting (17) into (16),
LRL
ξ
can be expressed
as the following (18),
{
}
{ }
2
,
2
,1
2
,1
2
ˆ
()-()
11
1()()()
22
11
1()()()
22
1
(1(21))
2
211
1
62
RFklmm
klFmm
klFmm
lFF
EHkl Hkl
LLll
Eekl Wk k
NPLL
LlLl
Eekl Wk k
NPLL
L
EeLPl
NP
LL
LNP
−
−
=++=

−−


−+++


−




−−


+−+++


−



−
++−+=
−
−−

+−

−

ξ
δ
δ
ξ
{ }
2
2
1
211
1(),
62
km
LL
Ek
LNP −



−−

+−

−

σ
δ
(17)
()( )
{ }
2
21
2
2121
().
6
LRLPRF
km
PPNP
NNN
LNPL Ek
NL
−
−
=++
−−−+

++


ξξξξ
σδ
(18)
4.2.2. Time Linear Interpolation
By LS estimation on pilot tones, time linear interpolation
on virtual pilot tones and frequency interpolation on data
tones, the MSE of channel estimation can be expressed as
2
,
LLLPRLF
PPNP
NNN
−
=++
ξξξξ
(19)
where
LF
ξ
is the MSE of frequency interpolation when
using time linear interpolation at virtual pilot tones. Us-
ing (12),
LF
ξ
can be obtained as shown in (20).
Substituting (20) into (19),
LLL
ξ
can be expressed as
the following (21),
{
}
{ }
2
,
2
1
,
2
1
,
2
ˆ()-()
11
1
22
()()
()() 2
11
1
22
()()
()() 2
1(1(21))
2
LFklmm
mm
klFm
mm
klFm
lF
EHkl Hkl
L
NP
kk Lll
Eekl Wk
LL
L
NP
kk lLl
Eekl Wk
LL
L
EeLPl
NP
ξ
δδ
δδ
−
−
=++=
−

−

−


− −

+++



−

+−

−


− −

+++



−
++−+=
−

D. L. WANG 450
2
2
1
211
1
62
()() 211
1.
622
F
mm
k
LL
LNP
kk LL
E
LNP
ξσ
δδ
−
−−

+−

−


− −−


+−


−



(20)
()( )
2
21
2
2121
6
()()
.
2
LLLPRF
mm
k
PPNP
NNN
LNPL
NL
kk
E
−
−
=++
−−−+
+


−


+





ξξξξ
δδ
σ
(21)
4.2.3. Comparison
Subtracting (21) from (18), the difference between
LRL
ξ
and
LLL
ξ
can be obtained as
(
)
(
)
{ }
2
2
21
1
2121
26
()()
().
2
LRLLLL
mm
kmk
LNPL
PP
NNNL
kk
EkE−
−
−−−+

−=++




−


×−





ξξσ
δδ
δ
(22)
From (22), one can notice that
1) Since N >> P,
2
2
P
N
σ
is negligible and the dif-
ferential MSE using (22) is approximately independent
with noise;
2) In a time-invariant frequency-selective channel,
LRL
ξ
is approximately equal to
LLL
ξ
; while in a
time-variant frequency-selective channel, the perform-
ance comparison depends on the specific channel varia-
tion;
3) Considering a real-valued channel variation, in low
noise environment, when 1
()()0
mm
kk
−
<
δδ and
()
m
k
>
δ
1
()
m
k
−
δ
,
LRLLLL
<
ξξ
;
4)
LRLLLLRL
−<−
ξξξξ
.
5. Numerical Results
The OFDM system under consideration is with N = 512
subcarriers, and 2L = 8 equispaced pilot tones in each
symbol. The length of cyclic prefix is 32. The interpola-
tion distances p = q = 1. The modulation is QPSK. The
pilot tones are all 1. For
063
j
≤≤
, in the odd OFDM
symbols, the pilot is inserted at the
(
)
18th
j
+ tone;
while in the even OFDM symbols, the pilot is inserted at
the
(
)
58th
j
+ tone. The six-ray multipath Rayleigh
fading channel is considered. The average power delay
profile is selected as
5
0
exp()
l
l
l
l
=
−
=
∑
λ
λ
,
05
l
≤≤
. (23)
Figure 3 shows the MSE performance of time inter-
polator and channel estimation in the time-invariant fre-
quency-selective channel, where one can see that time
linear interpolator generating less noise has a 3 dB lower
MSE than time replica at the virtual pilot tones. However,
for the corresponding channel estimation at the whole
OFDM tones, time linear interpolator performs similarly
to time replica due to a negligible noise.
Figure 4 shows the MSE performance in a time vary-
ing channel where the parameters are
{
}
1
()
km
Ek
−
δ
0.001
=
,
{
}
6
1
()10
km
Vark
−
−
=δ,
{
}
()0.002
km
Ek=−δ, and
{
}
6
()10
km
Vark
−
=δ, respectively. For interpolation at vir-
tual pilot tones, when
25
SNR
≤
dB, time linear inter-
polator performs better than time replica due to better
noise reduction; when SNR > 25 dB, time replica, which
guarantees a more accurate interpolation in a low noise
environment, performs better than linear interpolator.
While for the corresponding channel estimation, when
25
SNR
≤
dB, time linear interpolator performs very
similarly to time replica due to better noise reduction;
when SNR > 25 dB, time replica also performs better
than time linear interpolator.
Figure 5 shows the MSE performance in the time va-
rying channel where the parameters are
{
}
1
()
km
Ek
−
δ
010 2030
-95
-90
-85
-80
-75
-70
-65
-60
SNR[dB]
MSE[dB]
MSE of time interpolator
Time replica
Time linear interp
010 20 30
-95
-90
-85
-80
-75
-70
-65
-60
SNR[dB]
MSE[dB]
MSE of channel estimation
Time replica
Time linear interp
Figure 3. MSE of time interpolator and channel estimation
in time-invariant frequency-selective channel.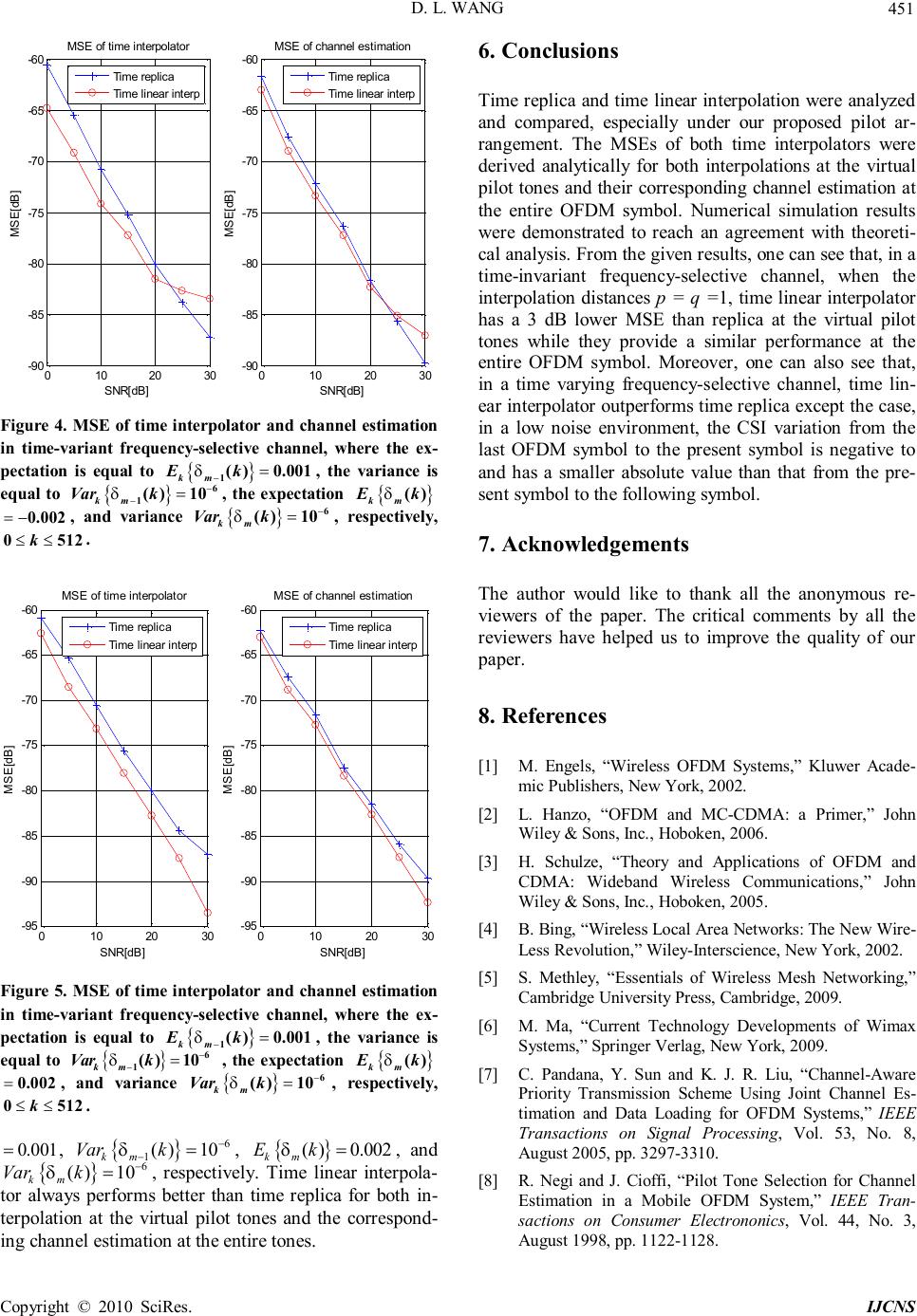

D. L. WANG
451
010 20 30
-90
-85
-80
-75
-70
-65
-60
SNR[dB]
MSE[dB]
MSE of time interpolator
Time replica
Time linear interp
010 20 30
-90
-85
-80
-75
-70
-65
-60
SNR[dB]
MSE[dB]
MSE of channel estimation
Time replica
Time linear interp
Figure 4. MSE of time interpolator and channel estimation
in time-variant frequency-selective channel, where the ex-
pectation is equal to
{
}
1
()0.001
km
Ekδ
−
=, the variance is
equal to
{
}
6
1
()10
km
Varkδ
−
−=, the expectation
{
}
()
km
Ek
δ
0.002
=− , and variance
{
}
6
()10
km
Varkδ
−
=, respectively,
0512
k≤≤ .
01020 30
-95
-90
-85
-80
-75
-70
-65
-60
SNR[dB]
MSE[dB]
MSE of time interpolator
Time replica
Time linear interp
01020 30
-95
-90
-85
-80
-75
-70
-65
-60
SNR[dB]
MSE[dB]
MSE of channel estimation
Time replica
Time linear interp
Figure 5. MSE of time interpolator and channel estimation
in time-variant frequency-selective channel, where the ex-
pectation is equal to
{
}
1
()0.001
km
Ekδ
−
=, the variance is
equal to
{
}
6
1
()10
km
Varkδ
−
−= , the expectation
{
}
()
km
Ek
δ
0.002
=, and variance
{
}
6
()10
km
Varkδ
−
=, respectively,
0512
k≤≤ .
0.001
=
,
{
}
6
1
()10
km
Vark
−
−=δ,
{
}
()0.002
km
Ek=δ, and
{
}
6
()10
km
Vark
−
=δ, respectively. Time linear interpola-
tor always performs better than time replica for both in-
terpolation at the virtual pilot tones and the correspond-
ing channel estimation at the entire tones.
6. Conclusions
Time replica and time linear interpolation were analyzed
and compared, especially under our proposed pilot ar-
rangement. The MSEs of both time interpolators were
derived analytically for both interpolations at the virtual
pilot tones and their corresponding channel estimation at
the entire OFDM symbol. Numerical simulation results
were demonstrated to reach an agreement with theoreti-
cal analysis. From the given results, one can see that, in a
time-invariant frequency-selective channel, when the
interpolation distances p = q =1, time linear interpolator
has a 3 dB lower MSE than replica at the virtual pilot
tones while they provide a similar performance at the
entire OFDM symbol. Moreover, one can also see that,
in a time varying frequency-selective channel, time lin-
ear interpolator outperforms time replica except the case,
in a low noise environment, the CSI variation from the
last OFDM symbol to the present symbol is negative to
and has a smaller absolute value than that from the pre-
sent symbol to the following symbol.
7. Acknowledgements
The author would like to thank all the anonymous re-
viewers of the paper. The critical comments by all the
reviewers have helped us to improve the quality of our
paper.
8. References
[1] M. Engels, “Wireless OFDM Systems,” Kluwer Acade-
mic Publishers, New York, 2002.
[2] L. Hanzo, “OFDM and MC-CDMA: a Primer,” John
Wiley & Sons, Inc., Hoboken, 2006.
[3] H. Schulze, “Theory and Applications of OFDM and
CDMA: Wideband Wireless Communications,” John
Wiley & Sons, Inc., Hoboken, 2005.
[4] B. Bing, “Wireless Local Area Networks: The New Wire-
Less Revolution,” Wiley-Interscience, New York, 2002.
[5] S. Methley, “Essentials of Wireless Mesh Networking, ”
Cambridge University Press, Cambridge, 2009.
[6] M. Ma, “Current Technology Developments of Wimax
Systems,” Springer Verlag, New York, 2009.
[7] C. Pandana, Y. Sun and K. J. R. Liu, “Channel-Aware
Priority Transmission Scheme Using Joint Channel Es-
timation and Data Loading for OFDM Systems,” IEEE
Transactions on Signal Processing, Vol. 53, No. 8,
August 2005, pp. 3297-3310.
[8] R. Negi and J. Cioffi, “Pilot Tone Selection for Channel
Estimation in a Mobile OFDM System,” IEEE Tran-
sactions on Consumer Electrononics, Vol. 44, No. 3,
August 1998, pp. 1122-1128.

D. L. WANG 452
[9] W. Zhang, X.-G. Xia and P. C. Ching, “Clustered Pilot
Tones for Carrier Frequency Offset Estimation in OF-
DM Systems,” IEEE Transactions on Wireless Communi-
cations , Vol. 6, No. 1, 2007, pp. 101-109.
[10] X. D. Dong, W.-S. Lu and A. C. K. Soong, “Linear Inter-
polation in Pilot Symbol Assisted Channel Estimation for
OFDM,” IEEE Transactions on Wireless Communica-
tions, Vol. 6, No. 5, May 2007, pp. 1910-1920.
[11] I. Budiarjo, I. Rashad and H. Nikookar, “On the Use of
Virtual Pilots with Decision Directed Method in OFDM
Based Cognitive Radio Channel Estimation Using 2x1-D
Wiener Filter, ” Proceedings of IEEE International Con-
ference on Communications, Beijing, May 2008, pp. 703-
707.
[12] Q. F. Huang, M. Ghogho and S. Freear, “Pilot Design for
MIMO OFDM Systems with Virtual Carriers,” IEEE
Transactions on Signal Processing, Vol. 57, No 5, May
2009, pp. 2024-2029.
[13] J. H. Zhang, W. Zhou, H. Sun and G.Y. Liu, “A Novel
Pilot Sequences Design for MIMO OFDM Systems with
Virtual Subcarriers,” Proceedings of Asia-Pacific Confe-
rence on Communications, Perth, 2007, pp. 501-504.
[14] R. Prasad, “OFDM for Wireless Communications Sys-
tems,” Artech House, Boston, 2004.
[15] A. R. S. Bahai, “Multi-Carrier Digital Communications,”
Springer Verlag, New York, 2004.
[16] K. Jihyung, P. Jeongho and H. Daesik, “Performance
Analysis of Channel Estimation in OFDM Systems,”
IEEE Signal Processing Letters, Vol. 12, No. 1, January
2005, pp. 60-62.
[17] P. Jeongho, K. Jihyung, P. Myonghee, K. Kyunbyoung,
K. Changeon and H. Daesik, “Performance Analysis of
Channel Estimation for OFDM Systems with Residual
Timing Offset, ” IEEE Transactions on Wireless Commu-
nications, Vol. 5, No. 7, July 2006, pp. 1622-1625.
[18] H. Myeongsu, Y. Takki, K. Jihyung and K. Kyungchul,
“OFDM Channel Estimation With Jammed Pilot Detector
Under Narrow-Band Jamming, ” IEEE Transactions on
Vehicular Technology, Vol. 57, No. 3, May 2008, pp.
1934-1939.
[19] A. Rosenzweig, Y. Steinberg and S. Shamai, “On Chann-
Els with Partial Channel State Information at the Trans-
mitter, ” IEEE Transactions on Information Theory, Vol.
51, No. 5, May 2005, pp. 1817-1830.
[20] S. Coleri, M. Ergen, A. Puri and A. Bahai, “Channel Esti-
Mation Techniques Based on Pilot Arrangement in OF-
DM Systems,” IEEE Transactions on Broadcasting, Vol.
48, No. 3, September 2002, pp.223-229.