Int. J. Communications, Network and System Sciences, 2010, 3, 425-429
doi:10.4236/ijcns.2010.35055 Published Online May 2010 (http://www.SciRP.org/journal/ijcns/)
A/D Restrictions (Errors) in Ultra-Wideband
Impulse Radios
Giorgos Tatsis1, Constantinos Votis1, Vasilis Raptis1, Vasilis Christofilakis1,2, Panos Kostarakis1
1Physics Department, University of Ioannina, Ioannina, Greece
2Siemens Enterprise Communications, Enterprise Products Development, Athens, Greece
[e-mail], [e-mail]
Received February 4, 2010; revised March 6, 2010; accepted April 20, 2010
Abstract
Ultra-Wideband Impulse Radio (UWB-IR) technologies, although are relatively easy in transmission but
they present difficulties in reception, in fact the reception of such waveform is a quite complicated matter.
The main reason is that in fully digital receiver the received waveform must be sampled at a rate of several
GHz. This paper focuses on the impact of the Analog to Digital (A/D) conversion stage that is used to sam-
ple the received waveform. More specifically we focus on the impact of the two main parameters that affect
the performance of the Software Defined Radio (SDR) system. These parameters are the bit resolution and
the time jittering. The influence of these parameters is deeply examined.
Keywords: UWB, Impulse Radio, ADC, Jitter Error, Quantization Error
1. Introduction
UWB transmission has recently received great attention
in academia and industry for applications in wireless
communications. A UWB system is defined as any radio
system that has a 10 dB fractional bandwidth larger than
20% of its center frequency, or has a 10 dB bandwidth
larger than 500 MHz. It is expected that many ap-
proaches used for short-range wireless communications
will be revaluated and a new industrial sector with high
data rate will be formed. Fully digital receiver for
UWB-IR requires the use of A/D conversion and SDR
techniques as described below. The RF waveform re-
ceived from the antenna is directly digitized from the
antenna via an A/D conversion stage. Then the digital
information derived from the UWB waveform is handled
and processed by a DSP. However, this process, intro-
duce new signal distortions, due to the new uncertainties
introduced, that are the jitter error and the quantization
error. The latter comes exclusively from the bit resolu-
tion of the A/D converter, while time jittering comes
merely from the aperture jitter of the ADC, and from
clock jitter of the sampling circuitry [1,2]. In this paper
we examine the impact of those two parameters on the
bit error rate performance of an UWB-IR fully digital
receiver. In UWB-IR systems a pulse train, consisting of
very short pulses and occupying very large spectrum [3],
is transmitted. Several modulation schemes are used such
as Bi-phase, Pulse Position, On-Off keying etc. [4]. In
this paper we choose Binary Pulse Position Modulation
(BPPM). We consider transmission through indoor mul-
tipath environment [5], in the presence of white Gaussian
noise. The performance of the system is evaluated by the
bit error probability (BEP) in terms of jitter and quanti-
zation noise. An expression of BEP is derived and nume-
rically results are presented.
2. Analog to Digital Conversion
During the A/D conversion additional noise is produced
at the output of the A/D converter due to two main rea-
sons: Quantization and Jitter error. The first is illustrated
in Figure 1 (a) and it is a result of the difference be-
tween the analog, continuous input signal and the digi-
tized output of the ADC. The finite ADC resolution
gives the form of the stairs-like signal. If an ADC has a
bit resolution of N bits, it means that the output signal
is coded at 2
N
different binary numbers, from 0 to
2
N
–1. Let assume that the input signals peak to peak
amplitude (
p
p
V) is the same with the ADC full-scale
voltage range. Then the corresponding quantization step
is /2
N
pp
QV. An amplitude value at the input is
mapped to the nearest N bit binary number and the

G. TATSIS ET AL. 426
absolute difference between input-output can be from
zero to /2Q, thus the quantization error is from
/2Q to /2Q. We assume that the input signal can
take any random value within a quantization step, with
equal probability. Therefore the distribution of quantiza-
tion error is uniform and its probability density function
()
f
x, is shown in Figure 1(b). Obviously, it has a mean
of zero and it is easy to prove that the standard deviation
of quantization error is /12
qQ
 , as follows,
32
222 2
22
0
2
122
() 24 12
QQ
qQ
QQ
xfxdxxdx xdx
QQQ



 


The second error that concerns our study is called jitter
error and it is a result of the non infinite timing precision
of the sampling procedure and the ADC imperfections.
The fact is that there is an uncertainty at the sampling
time which causes an uncertainty at the input voltage of
the signal. This effect is shown in Figure 2. Let the input
signal at an A/D converter be ()Vt . We focus at the
A
mp
li
tu
d
e
Time
(a)
-Q/2 Q/2 x
f (x)
1/Q
(b)
Figure 1. (a) Digitization of an analog continuous signal
(dotted line) to discrete and quantized signal (normal line);
(b) Uniform distribution ()
f
x of quantization error x.
time 1 t, corresponding at a multiplicate of sampling
period. Due to jitter effect the sample taken by the ADC
is the one at the time 1
j
tt

, where
j
t is a random
variable, assuming normally distributed with zero mean
and standard deviation
j

. The corresponding voltage
error is then, 11 ()()
jj
VVtt Vt

 . By rewriting this
expression we have,
11
11
()()
()() j
j
jj
j
Vtt Vt
VVtt Vtt
t

 

 




(1)
For small
j
t

we can approximate the expression in
the brackets with the first derivative of ()Vt [6], and
obtaining,
1
'
1
() ()
jjj
tt
dV t
VttVt
dt 

 

 (2)
3. Signal Model Description
The transmitted pulses have the form of a Gauss mono-
cycle, i.e. the first derivative of a standard Gauss pulse.
Figure 3 shows a schematic representation of the BPPM
modulated transmitted signal. The bit period is
f
T (fra-
me period) and the time offset  represents the modu-
lation index. Time is divided into frames, the period of
V(t)
∆V
j
t
1
t
1
+ ∆t
j
t
∆t
j
Figure 2. Jitter error effect.
T
f
T
f
00 1
Figure 3. BPPM signaling.

G. TATSIS ET AL. 427
the frames is
f
T. We determine the symbol by its posi-
tion within each frame. A logic “0” is a pulse at the be-
ginning of the frame, while a logic ‘1’ is delayed by a
small amount of time . The modulated pulses wave-
form ()
s
tis expressed by Equation 3 below,
1
0
() ()
N
bfj
j
s
tEwtjTb



 (3)
where, ()wt is the pulse shape (first derivative of a
Gaussian pulse) normalized to have total energy
2
() 1wt dt

 
, b
E is the energy per bit,
f
T is the
frame period,
j
b is the j-th bit,  is the BPPM modu-
lation index, N is the total number of transmitted
pulses. w

is related to the pulse width with the rela-
tionship 2
p
w
T

 , where
p
T represents the width of
the pulse. The modulation index  is chosen to satisfy
the orthogonality of the transmitted symbols, i.e.,
() ()0wt wtdt

  
. We choose  greater than the
pulse duration, i.e.,
p
T.
4. Theoretical Analysis of Error Probability
In order to derive an expression for the probability of
error, we consider the transmit and receive system model
shown in Figure 4. The transmitted signal, ()
s
t, de-
scribed above, propagates through a multipath channel
with impulse response ()ht. Then it is converted from
analog to digital using an A/D converter. As mentioned
above the input signal is sampled at the ADC frequency
and quantized with corresponding ADC resolution. For
the detection of the symbols, a matched filtering tech-
nique is used. The matched filter is constructed by two
correlators. The received signal is correlated with the
expected symbols and the output is the difference of
those. The output is sampled every frame period.
We assume perfect channel estimation and synchroni-
zation. From this point, the analysis continuous for the
first frame period, i.e., 0
f
tT . We use vector notation,
which represents the sampled versions of the signals.
Figure 4. System transmission-reception model.
All the vectors has length,
f
fs
NTf, where
f
T is
the frame period and
s
f
is the sampling frequency. The
templates for the two symbols (01 ,xx) are the transmit-
ted symbols for ‘0’ and ‘1’ respectively after the channel,
n is Gaussian process, representing total additive noise,
with a mean value of zero and a double side power spec-
tral density, 0/2N.
The channel impulse response, corresponding to the
IEEE 802.15.3a model [5] for indoor multipath environ-
ments, is given by 1
0
()( )
L
ll
l
ht t






, where L is
the total resolvable channel paths, ,
ll

 are the gain
coefficient and time delay, respectively, for the corre-
sponding l path. Thus the transmitter signal after the
channel is expressed as follows,
1
0
() ()()()
L
ll
l
xtsh tast



 
 (4)
where (*) denotes convolution.
The received discrete signal r is given in Equation 5
below,
j
q

r=xnnn (5)
where, 22
0
(0,),/ 2
nn
NN  n is the total additive
noise at the receiver,
j
n is the noise vector due to jitter
error and by using Equation 2. we have: 2 (0, ),
j
jit
N  n


T
22''
jit j
 xx and q n is the noise term due to
quantization noise i.e. (,),
22 12
qq
QQ Q
U
 n.
The derivative ' x is calculated from Equation 3 and
Equation 4, as follows,
1
0
11
00
()( )
()
L
ll
l
NL
bfjl
jl
dd
xt ast
dt dt
d
EwtjTb
dt











(6)
and by taking the discrete (sampled) vector. The wave-
form ()wt as mentioned before is the first derivative of
a gauss monopulse, thus ()
dwt
dt
is the second deriva
tive of the pulse. To obtain an expression for the prob-
ability of error on symbol detection, we must first define
the decision metric at the output of the correlators in
Figure 4 at time
f
tT

. For simplicity we consider the
transmission of a ‘0’ and in the same way we can derive
an expression for the ‘1’. The decision metric is then,



 
 





T
T
0001001
T
T
001 01
T
TT
00010 1
TT
01 01
(0)( )
jq
jq
jq
xx xxjq
D
RR



 
rx-xx nnnx-x
xx -xnnnx -x
xxxxnnnx-x
n nx-xnx-x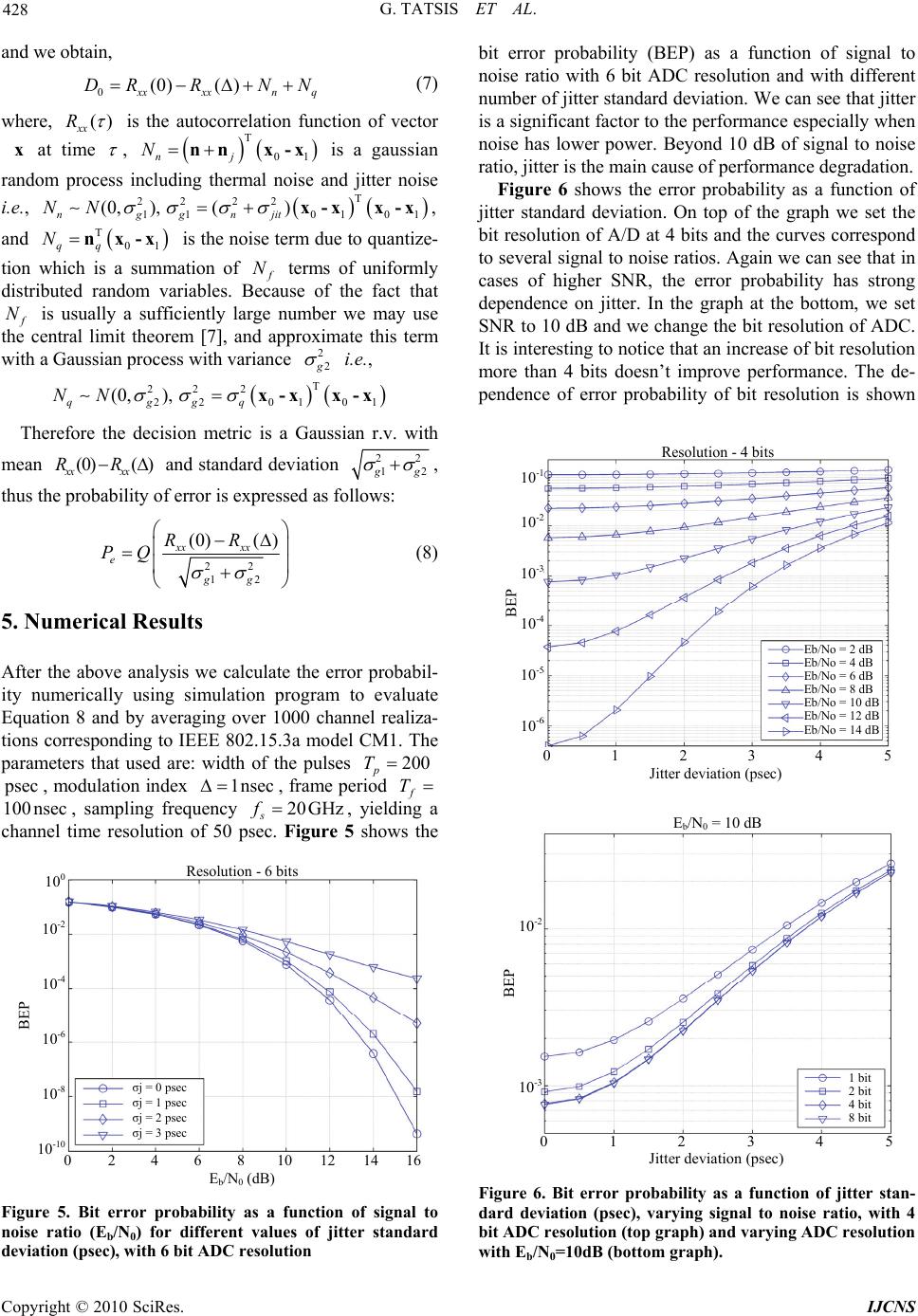

G. TATSIS ET AL. 428
and we obtain,
0(0)( )
x
xxx nq
DR RNN
(7)
where, ()
xx
R

is the autocorrelation function of vector
x at time

,


T
01 nj
Nnn x-x is a gaussian
random process including thermal noise and jitter noise
i.e.,



T
22 22
1101 01
(0,),()
nggn jit
NN   x-xx-x ,
and

T
01 qq
Nnx-x is the noise term due to quantize-
tion which is a summation of
f
N terms of uniformly
distributed random variables. Because of the fact that
f
N is usually a sufficiently large number we may use
the central limit theorem [7], and approximate this term
with a Gaussian process with variance 2
2
g

i.e.,

T
22 2
22 0101
(0, ),
qggq
NN   x-xx-x
Therefore the decision metric is a Gaussian r.v. with
mean (0)( )
xx xx
RR and standard deviation 22
12
g
g

 ,
thus the probability of error is expressed as follows:
22
12
(0)( )
xx xx
e
gg
RR
PQ







(8)
5. Numerical Results
After the above analysis we calculate the error probabil-
ity numerically using simulation program to evaluate
Equation 8 and by averaging over 1000 channel realiza-
tions corresponding to IEEE 802.15.3a model CM1. The
parameters that used are: width of the pulses 200
p
T

p
sec , modulation index 1nsec , frame period f T

100 nsec, sampling frequency 20GHz
s
f, yielding a
channel time resolution of 50 psec. Figure 5 shows the
Resolution - 6 bits
E
b
/N
0
(
dB
)
BEP
10
0
10
-2
10
-4
10
-6
10
-8
10
-10
0 2 4 6 8 10 12 14 16
σj = 0 psec
σj = 1 psec
σj = 2 psec
σj = 3 psec
Figure 5. Bit error probability as a function of signal to
noise ratio (Eb/N0) for different values of jitter standard
deviation (psec), with 6 bit ADC resolution
bit error probability (BEP) as a function of signal to
noise ratio with 6 bit ADC resolution and with different
number of jitter standard deviation. We can see that jitter
is a significant factor to the performance especially when
noise has lower power. Beyond 10 dB of signal to noise
ratio, jitter is the main cause of performance degradation.
Figure 6 shows the error probability as a function of
jitter standard deviation. On top of the graph we set the
bit resolution of A/D at 4 bits and the curves correspond
to several signal to noise ratios. Again we can see that in
cases of higher SNR, the error probability has strong
dependence on jitter. In the graph at the bottom, we set
SNR to 10 dB and we change the bit resolution of ADC.
It is interesting to notice that an increase of bit resolution
more than 4 bits doesn’t improve performance. The de-
pendence of error probability of bit resolution is shown
Resolution - 4 bits
Jitter deviation (psec)
BEP
10
-1
10
-2
10
-3
10
-4
10
-5
10
-6
0 1 2 3 4 5
Eb/No = 2 dB
Eb/No = 4 dB
Eb/No = 6 dB
Eb/No = 8 dB
Eb/No = 10 dB
Eb/No = 12 dB
Eb/No = 14 dB
E
b
/N0 = 10 dB
Jitter deviation (psec)
BEP
10-2
10-3
0 1 2 3 4 5
1 bit
2 bit
4 bit
8 bit
Figure 6. Bit error probability as a function of jitter stan-
dard deviation (psec), varying signal to noise ratio, with 4
bit ADC resolution (top graph) and varying ADC resolution
with Eb/N0=10dB (bottom graph).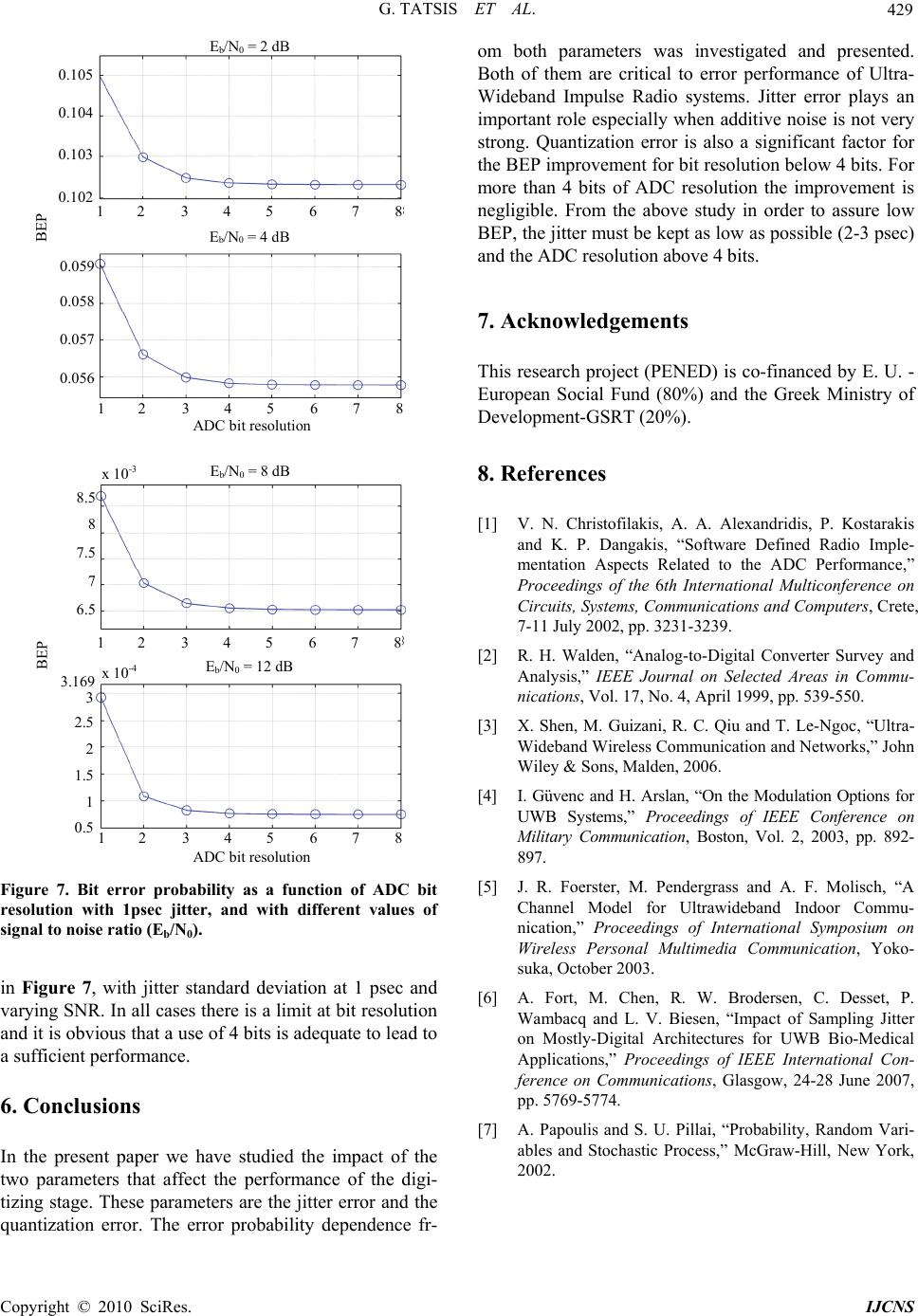

G. TATSIS ET AL. 429
E
b
/N0 = 2 dB
ADC bit resolution
BEP
0.105
0.104
0.103
0.102
1 2 3 4 5 6 7 8
E
b
/N0 = 4 dB
1 2 3 4 5 6 7 8
0.059
0.058
0.057
0.056
E
b
/N
0
= 8 dB
ADC bit resolution
BEP
8.5
8
7.5
7
6.5
1 2 3 4 5 6 7 8
E
b
/N
0
= 12 dB
1 2 3 4 5 6 7 8
3
2.5
2
1.5
1
0.5
x 10
-3
x 10
-4
3.169
Figure 7. Bit error probability as a function of ADC bit
resolution with 1psec jitter, and with different values of
signal to noise ratio (Eb/N0).
in Figure 7, with jitter standard deviation at 1 psec and
varying SNR. In all cases there is a limit at bit resolution
and it is obvious that a use of 4 bits is adequate to lead to
a sufficient performance.
6. Conclusions
In the present paper we have studied the impact of the
two parameters that affect the performance of the digi-
tizing stage. These parameters are the jitter error and the
quantization error. The error probability dependence fr-
om both parameters was investigated and presented.
Both of them are critical to error performance of Ultra-
Wideband Impulse Radio systems. Jitter error plays an
important role especially when additive noise is not very
strong. Quantization error is also a significant factor for
the BEP improvement for bit resolution below 4 bits. For
more than 4 bits of ADC resolution the improvement is
negligible. From the above study in order to assure low
BEP, the jitter must be kept as low as possible (2-3 psec)
and the ADC resolution above 4 bits.
7. Acknowledgements
This research project (PENED) is co-financed by E. U. -
European Social Fund (80%) and the Greek Ministry of
Development-GSRT (20%).
8. References
[1] V. N. Christofilakis, A. A. Alexandridis, P. Kostarakis
and K. P. Dangakis, “Software Defined Radio Imple-
mentation Aspects Related to the ADC Performance,”
Proceedings of the 6th International Multiconference on
Circuits, Systems, Communications and Computers, Crete,
7-11 July 2002, pp. 3231-3239.
[2] R. H. Walden, “Analog-to-Digital Converter Survey and
Analysis,” IEEE Journal on Selected Areas in Commu-
nications, Vol. 17, No. 4, April 1999, pp. 539-550.
[3] X. Shen, M. Guizani, R. C. Qiu and T. Le-Ngoc, “Ultra-
Wideband Wireless Communication and Networks,” John
Wiley & Sons, Malden, 2006.
[4] I. Güvenc and H. Arslan, “On the Modulation Options for
UWB Systems,” Proceedings of IEEE Conference on
Military Communication, Boston, Vol. 2, 2003, pp. 892-
897.
[5] J. R. Foerster, M. Pendergrass and A. F. Molisch, “A
Channel Model for Ultrawideband Indoor Commu-
nication,” Proceedings of International Symposium on
Wireless Personal Multimedia Communication, Yoko-
suka, October 2003.
[6] A. Fort, M. Chen, R. W. Brodersen, C. Desset, P.
Wambacq and L. V. Biesen, “Impact of Sampling Jitter
on Mostly-Digital Architectures for UWB Bio-Medical
Applications,” Proceedings of IEEE International Con-
ference on Communications, Glasgow, 24-28 June 2007,
pp. 5769-5774.
[7] A. Papoulis and S. U. Pillai, “Probability, Random Vari-
ables and Stochastic Process,” McGraw-Hill, New York,
2002.